人教版 八年级数学 下册 第18章 平行四边形 综合训练 (word版 含解析)
文档属性
| 名称 | 人教版 八年级数学 下册 第18章 平行四边形 综合训练 (word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 352.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 08:25:30 | ||
图片预览


文档简介
人教版 八年级数学 第18章 平行四边形 综合训练
一、选择题(本大题共10道小题)
1. (2020·衡阳)如图,在四边形ABCD中,对角线AC和BD相交于点O.下列条件不能判断四边形ABCD是平行四边形的是 ( )
A.?AB∥DC?,AD∥BC B.?AB=?DC,AD=?BC
C.?AB∥DC,AD?=BC D.OA=?OC,OB?=OD
2. (2020·通辽)如图,AD是△ABC的中线,四边形ADCE是平行四边形,增加下列条件,能判断?ADCE是菱形的是( )
A.∠BAC=90° B.∠DAE=90° C.AB=AC D.AB=AE
3. (2020·南通) 下列条件中,能判定□ABCD是菱形的是
A.AC=BD B.AB⊥BC C.AD=BD D.AC⊥BD
4. 如图,在矩形中,的交点在上,图中面积相等的四边形有( )
A.对 B.对 C.对 D.对
5. 如图,ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点,则下列说法正确的是
A.EH=HG
B.四边形EFGH是平行四边形
C.AC⊥BD
D.△ABO的面积是△EFO的面积的2倍
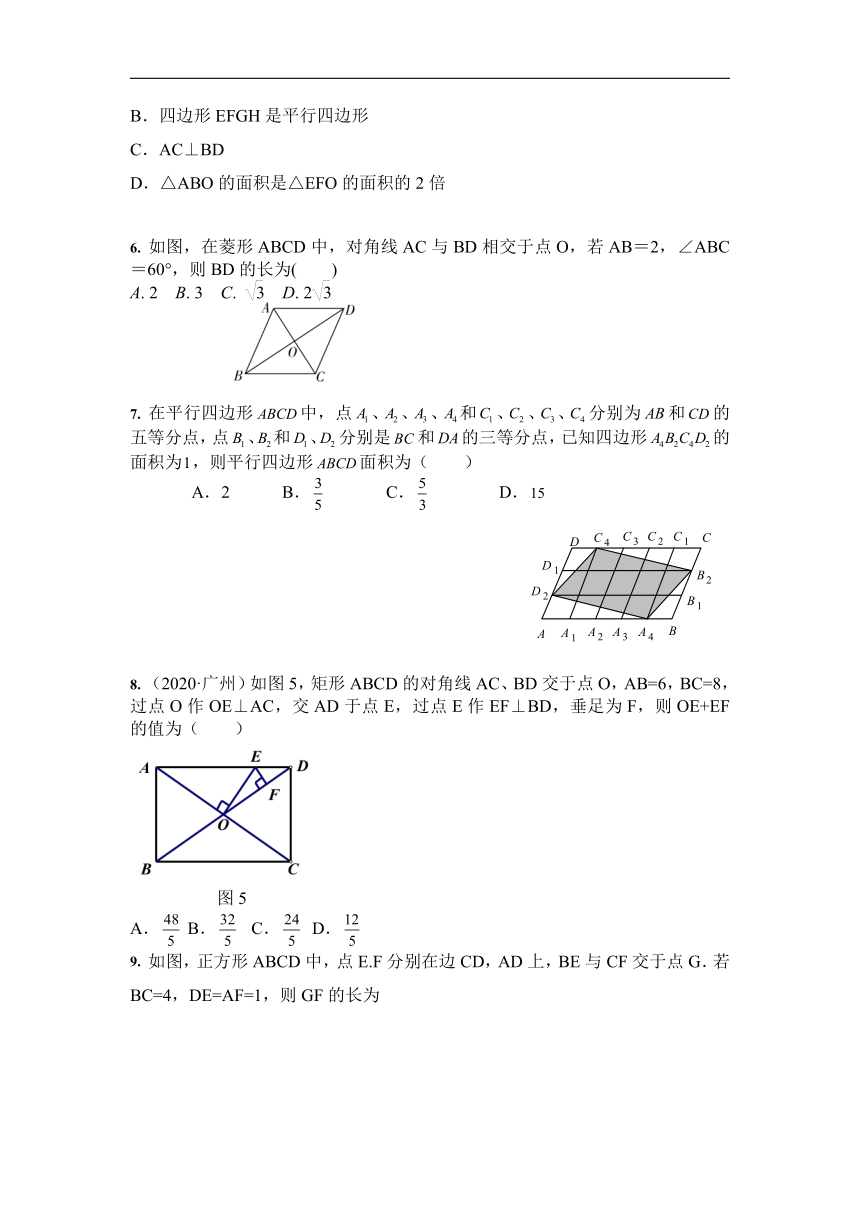
6. 如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为( )
A. 2 B. 3 C. D. 2
7. 在平行四边形中,点、、、和、、、分别为和的五等分点,点、和、分别是和的三等分点,已知四边形的面积为,则平行四边形面积为( )
A.2 B. C. D.
8. (2020·广州)如图5,矩形ABCD的对角线AC、BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为( )
图5
A. B. C. D.
9. 如图,正方形ABCD中,点E.F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则GF的长为
A. B. C. D.
10. (2020·东营)如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N,下列结论:①△APE≌△AME;②PM+PN=AC;③;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是( )
A. ①②③④ B. ①②③⑤ C. ①②③④⑤ D. ③④⑤
二、填空题(本大题共6道小题)
11. 如图,?ABCD中,AC=8,BD=6,AD=a,则a的取值范围是________.
12. 菱形的周长为,两邻角度数之比为,则菱形较短的对角线的长度为
13. 如图,如果要使平行四边形成为一个菱形,需要添加一个条件,那么你添加的条件是 .
14. 如图,已知等边三角形的边长为,是内一点,,,点分别在上,则
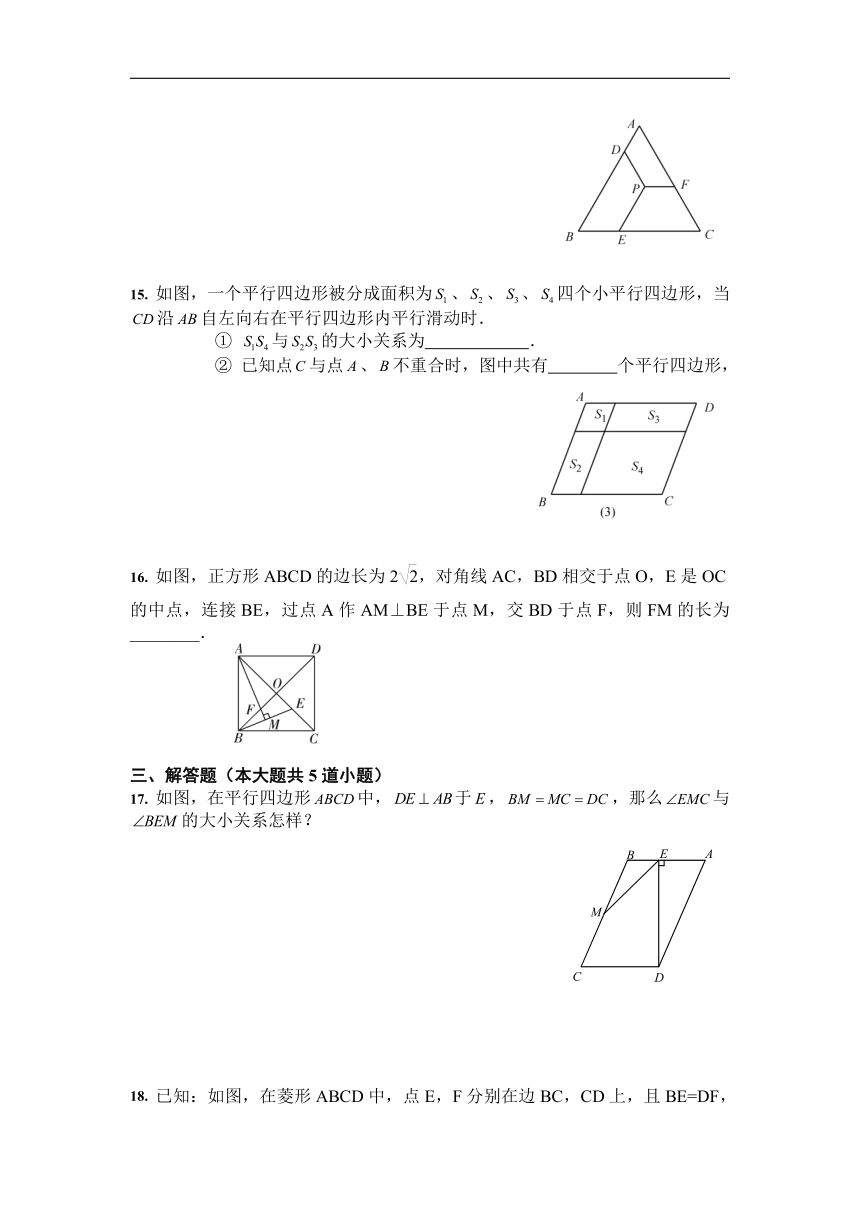
15. 如图,一个平行四边形被分成面积为、、、四个小平行四边形,当沿自左向右在平行四边形内平行滑动时.
① 与的大小关系为 .
② 已知点与点、不重合时,图中共有 个平行四边形,
16. 如图,正方形ABCD的边长为2,对角线AC,BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为________.
三、解答题(本大题共5道小题)
17. 如图,在平行四边形中,于,,那么与的大小关系怎样?
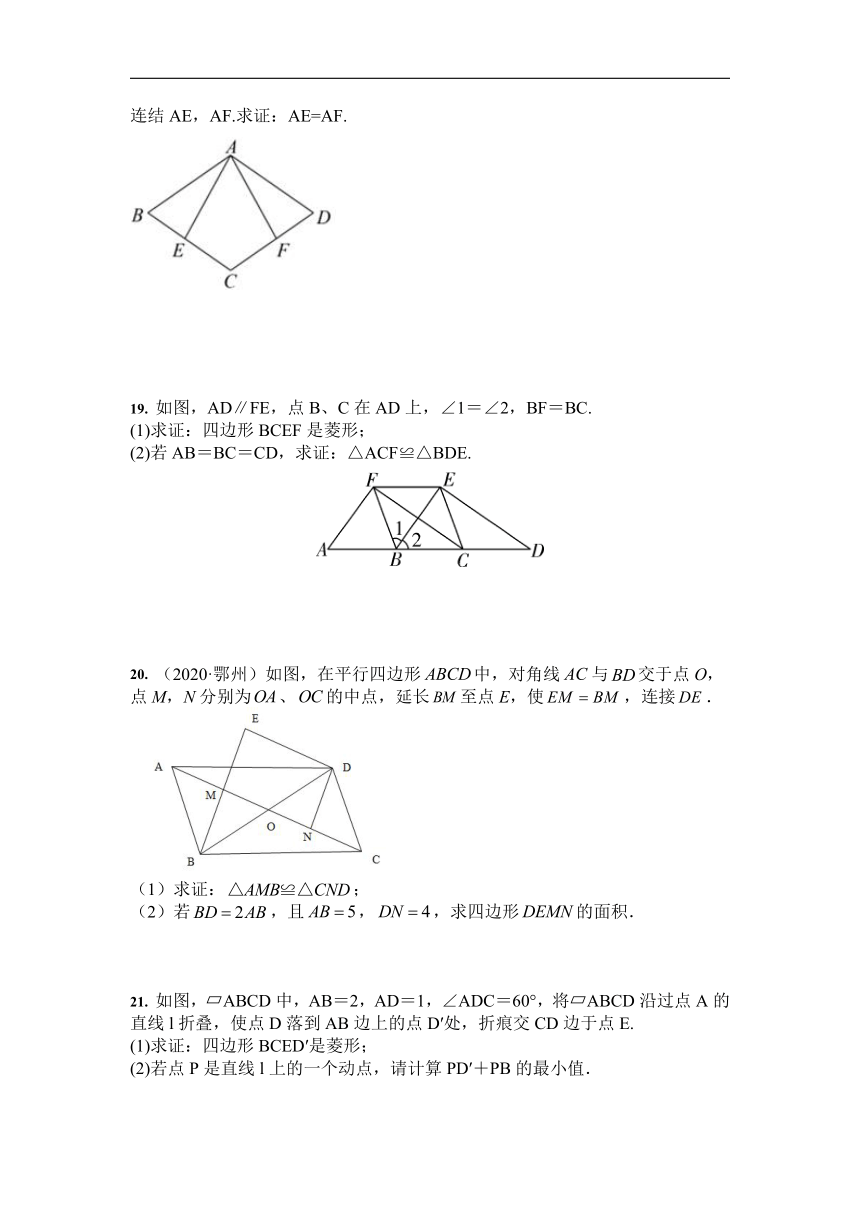
18. 已知:如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连结AE,AF.求证:AE=AF.
19. 如图,AD∥FE,点B、C在AD上,∠1=∠2,BF=BC.
(1)求证:四边形BCEF是菱形;
(2)若AB=BC=CD,求证:△ACF≌△BDE.
20. (2020·鄂州)如图,在平行四边形中,对角线与交于点O,点M,N分别为、的中点,延长至点E,使,连接.
(1)求证:;
(2)若,且,,求四边形的面积.
21. 如图,?ABCD中,AB=2,AD=1,∠ADC=60°,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P是直线l上的一个动点,请计算PD′+PB的最小值.
人教版 八年级数学 第18章 平行四边形 综合训练-答案
一、选择题(本大题共10道小题)
1. 【答案】C
【解析】本题考查了平行四边形的判定.注意掌握举反例的解题方法是解本题的关键.∵AB∥DC?? AD∥BC,∴四边形ABCD是平行四边形,故A选项能判定这个四边形是平行四边形;∵AB=DC?? AD=BC,∴四边形ABCD是平行四边形,故B选项能判定这个四边形是平行四边形;、∵AB∥DC?? AD=BC,∴四边形ABCD是平行四边形或等腰梯形,故C选项不能判定这个四边形是平行四边形.∵AO=CO?? BO=DO,∴四边形ABCD是平行四边形,故D选项能判定这个四边形是平行四边形;故选C.
2. 【答案】A
【解析】若∠BAC=90°,又因为AD是△ABC的中线,根据“直角三角形斜边上的中线等于斜边的一半”可得AD=CD,根据“有一组邻边相等的平行四边形是菱形”可证?ADCE是菱形.
3. 【答案】D
【解析】根据菱形的定义和判断定理判断.定义:有一组邻边相等的平行四边形是菱形;判断定理:对角线互相垂直的平行四边形是菱形.只有D能够判断出四边形ABCD是菱形.故选D.
4. 【答案】D
5. 【答案】B
【解析】∵E,F,G,H分别是AO,BO,CO,DO的中点,在ABCD中,AB=2,AD=4,
∴EH=AD=2,HG=AB=1,∴EH≠HG,故选项A错误;
∵E,F,G,H分别是AO,BO,CO,DO的中点,
∴EH=,
∴四边形EFGH是平行四边形,故选项B正确;
由题目中的条件,无法判断AC和BD是否垂直,故选项C错误;
∵点E、F分别为OA和OB的中点,
∴EF=,EF∥AB,∴△OEF∽△OAB,∴,
即△ABO的面积是△EFO的面积的4倍,故选项D错误,
故选B.
6. 【答案】D 【解析】∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴AB=BC=AC=2,∵四边形ABCD是菱形,∴∠AOB=90°,AO=AC=1,∴BO==,∴BD=2OB=2.
7. 【答案】C
8. 【答案】C
【解析】本题考查了矩形的性质,由勾股定理可得AC=10,再由矩形的对角线相等且互相平分的性质可得,OA=OD=5. △ABD的面积为24,OA为△ABD 的中线,由中线等分面积可得,△AOD的面积为12.再由等面积法即可得OE+EF的值.过程如下:
∵
∴ 即,∴OE+EF=,因此本题选C.
9. 【答案】A
【解析】正方形ABCD中,∵BC=4,
∴BC=CD=AD=4,∠BCE=∠CDF=90°,
∵AF=DE=1,∴DF=CE=3,∴BE=CF=5,
在△BCE和△CDF中,,
∴△BCE≌△CDF(SAS),∴∠CBE=∠DCF,
∵∠CBE+∠CEB=∠ECG+∠CEB=90°=∠CGE,
cos∠CBE=cos∠ECG=,
∴,CG=,∴GF=CF﹣CG=5﹣=,
故选A.
10. 【答案】B
【解析】本题考查了垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质,是常见问题的综合,灵活的运用所学知识是解答本题的关键.综合应用垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质等知识,逐个判断5个结论的正确性,得出结论.
①∵正方形ABCD,∴∠APE=∠AME=45°,∵PM⊥AE,∴∠AEP=∠AEM=90°,∵AE=AE,∴△APE≌△AME(ASA);
②过点N作NQ⊥AC于点Q,则四边形PNQE是矩形,∴PN=EQ,∵正方形ABCD,∴∠PAE=∠MAE=45°,∵PM⊥AE,∴∠PEA=45°,∴∠PAE=∠APE,PE=NQ,∴△APE等腰直角三角形,∴AE=PE,同理得:△NQC等腰直角三角形,∴NQ=CQ,∵△APE≌△AME,∴PE=ME,∴PE=ME= NQ=CQ,∴PM=AE+CQ,∴PM+PN=AE+CQ+EQ=AC,即PM+PN=AC成立;
③∵正方形ABCD,∴AC⊥BD,∴∠EOF是直角,∵过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,∴∠PEO和∠PFO是直角,∴四边形PFOE是矩形,∴PF=OE,在Rt△PEO中,有PE2+OE2=PO2,∴PE2+PF2=PO2,即PE2+PF2=PO2成立;
④△BNF是等腰直角三角形,点P不在AB的中点时,△POF不是等腰直角三角形,所以△POF与△BNF不一定相似,即△POF∽△BNF不一定成立;
⑤∵△AMP是等腰直角三角形,△PMN∽△AMP,∴△PMN是等腰直角三角形,∵∠MPN=90°,∴PM=PN,∵AP=PM,BP=PN,∴AP=BP,∴点P是AB的中点,又∵O为正方形的对称中点,∴点O在M、N两点的连线上.综上,①②③⑤成立,即正确的结论有4个,答案选B.
二、填空题(本大题共6道小题)
11. 【答案】1<a<7 【解析】如解图,对角线AC,BD相交于点O,则OA=AC=4,OD=BD=3,在△OAD中,OA-OD<AD<OA+OD,即1<a<7.
12. 【答案】
13. 【答案】
14. 【答案】
15. 【答案】①;②
16. 【答案】 【解析】∵四边形ABCD为正方形,∴AO=BO,∠AOF=∠BOE=90°,∵AM⊥BE,∠AFO=∠BFM,∴∠FAO=∠EBO,在△AFO和△BEO中,,∴△AFO≌△BEO(ASA),∴FO=EO,∵正方形ABCD的边长为2,E是OC的中点,∴FO=EO=1=BF,BO=2,∴在Rt△BOE中,BE==,由∠FBM=∠EBO,∠FMB=∠EOB,可得△BFM∽△BEO,∴=,即=,∴FM=.
三、解答题(本大题共5道小题)
17. 【答案】
延长交的延长线于,连结,
∵,,,
∴,∴是的中点.
∵,,∴.
在中,∵,
∴,又∵,
∴,又∴,
而,∴.
18. 【答案】
∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
∵BE=DF,∴△ABE≌△ADF,∴AE=CF.
19. 【答案】
证明:(1)∵AD∥EF,∴∠FEB=∠2.
∵∠1=∠2,∴∠FEB=∠1.∴BF=EF.∵BF=BC,
∴BC=EF.∴四边形BCEF是平行四边形.
∵BF=BC.∴四边形BCEF是菱形.
(2)∵EF=BC,AB=BC=CD,AD∥FE.
∴四边形ABEF、四边形CDEF均为平行四边形,
∴AF=BE,FC=ED.
又∵AC=2BC=BD.∴△ACF≌△BDE.
20. 【答案】
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,ABCD,OA=OC,
∴∠BAC=∠DCA,
又点M,N分别为、的中点,
∴,
在和中,
,
∴.
(2)BD=2BO,又已知BD=2AB,
∴BO=AB,∴△ABO为等腰三角形;
又M为AO的中点,
∴由等腰三角形的“三线合一”性质可知:BM⊥AO,
∴∠BMO=∠EMO=90°,
同理可证△DOC也为等腰三角形,
又N是OC的中点,
∴由等腰三角形的“三线合一”性质可知:DN⊥CO,
∠DNO=90°,
∵∠EMO+∠DNO=90°+90°=180°,
∴EMDN,
又已知EM=BM,由(1)中知BM=DN,
∴EM=DN,
∴四边形EMND平行四边形,
又∠EMO=90°,∴四边形EMND为矩形,
在Rt△ABM中,由勾股定理有:,
∴AM=CN=3,
∴MN=MO+ON=AM+CN=3+3=6,
∴.
21. 【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,
由折叠性质可知,∠D=∠AD′E=60°,
∴∠AD′E=∠B=60°,
∴ED′∥BC,
又∵EC∥D′B,
∴四边形BCED′是平行四边形,(4分)
∴ED′=BC=AD=1,
∴DE=ED′=1,
又DC=AB=2,
∴EC=1,
∴EC=ED′,
∴四边形BCED′是菱形.(6分)
(2)
解图
解:如解图所示,由折叠性质PD′=PD,BD之长即为所求,(8分)
作DG⊥BA的延长线于点G,
∵∠DAB=120°,
∴∠DAG=60°,
∵∠G=90°,
∴∠ADG=30°,
在Rt△ADG中,AD=1,
∴AG=,DG=,(9分)
∵AB=2,
∴BG=,
在Rt△BDG中,由勾股定理得:BD2=BG2+DG2=7,
∴BD=,
即PD′+PB的最小值为.(10分)
一、选择题(本大题共10道小题)
1. (2020·衡阳)如图,在四边形ABCD中,对角线AC和BD相交于点O.下列条件不能判断四边形ABCD是平行四边形的是 ( )
A.?AB∥DC?,AD∥BC B.?AB=?DC,AD=?BC
C.?AB∥DC,AD?=BC D.OA=?OC,OB?=OD
2. (2020·通辽)如图,AD是△ABC的中线,四边形ADCE是平行四边形,增加下列条件,能判断?ADCE是菱形的是( )
A.∠BAC=90° B.∠DAE=90° C.AB=AC D.AB=AE
3. (2020·南通) 下列条件中,能判定□ABCD是菱形的是
A.AC=BD B.AB⊥BC C.AD=BD D.AC⊥BD
4. 如图,在矩形中,的交点在上,图中面积相等的四边形有( )
A.对 B.对 C.对 D.对
5. 如图,ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点,则下列说法正确的是
A.EH=HG
B.四边形EFGH是平行四边形
C.AC⊥BD
D.△ABO的面积是△EFO的面积的2倍
6. 如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为( )
A. 2 B. 3 C. D. 2
7. 在平行四边形中,点、、、和、、、分别为和的五等分点,点、和、分别是和的三等分点,已知四边形的面积为,则平行四边形面积为( )
A.2 B. C. D.
8. (2020·广州)如图5,矩形ABCD的对角线AC、BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为( )
图5
A. B. C. D.
9. 如图,正方形ABCD中,点E.F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则GF的长为
A. B. C. D.
10. (2020·东营)如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N,下列结论:①△APE≌△AME;②PM+PN=AC;③;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是( )
A. ①②③④ B. ①②③⑤ C. ①②③④⑤ D. ③④⑤
二、填空题(本大题共6道小题)
11. 如图,?ABCD中,AC=8,BD=6,AD=a,则a的取值范围是________.
12. 菱形的周长为,两邻角度数之比为,则菱形较短的对角线的长度为
13. 如图,如果要使平行四边形成为一个菱形,需要添加一个条件,那么你添加的条件是 .
14. 如图,已知等边三角形的边长为,是内一点,,,点分别在上,则
15. 如图,一个平行四边形被分成面积为、、、四个小平行四边形,当沿自左向右在平行四边形内平行滑动时.
① 与的大小关系为 .
② 已知点与点、不重合时,图中共有 个平行四边形,
16. 如图,正方形ABCD的边长为2,对角线AC,BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为________.
三、解答题(本大题共5道小题)
17. 如图,在平行四边形中,于,,那么与的大小关系怎样?
18. 已知:如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连结AE,AF.求证:AE=AF.
19. 如图,AD∥FE,点B、C在AD上,∠1=∠2,BF=BC.
(1)求证:四边形BCEF是菱形;
(2)若AB=BC=CD,求证:△ACF≌△BDE.
20. (2020·鄂州)如图,在平行四边形中,对角线与交于点O,点M,N分别为、的中点,延长至点E,使,连接.
(1)求证:;
(2)若,且,,求四边形的面积.
21. 如图,?ABCD中,AB=2,AD=1,∠ADC=60°,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P是直线l上的一个动点,请计算PD′+PB的最小值.
人教版 八年级数学 第18章 平行四边形 综合训练-答案
一、选择题(本大题共10道小题)
1. 【答案】C
【解析】本题考查了平行四边形的判定.注意掌握举反例的解题方法是解本题的关键.∵AB∥DC?? AD∥BC,∴四边形ABCD是平行四边形,故A选项能判定这个四边形是平行四边形;∵AB=DC?? AD=BC,∴四边形ABCD是平行四边形,故B选项能判定这个四边形是平行四边形;、∵AB∥DC?? AD=BC,∴四边形ABCD是平行四边形或等腰梯形,故C选项不能判定这个四边形是平行四边形.∵AO=CO?? BO=DO,∴四边形ABCD是平行四边形,故D选项能判定这个四边形是平行四边形;故选C.
2. 【答案】A
【解析】若∠BAC=90°,又因为AD是△ABC的中线,根据“直角三角形斜边上的中线等于斜边的一半”可得AD=CD,根据“有一组邻边相等的平行四边形是菱形”可证?ADCE是菱形.
3. 【答案】D
【解析】根据菱形的定义和判断定理判断.定义:有一组邻边相等的平行四边形是菱形;判断定理:对角线互相垂直的平行四边形是菱形.只有D能够判断出四边形ABCD是菱形.故选D.
4. 【答案】D
5. 【答案】B
【解析】∵E,F,G,H分别是AO,BO,CO,DO的中点,在ABCD中,AB=2,AD=4,
∴EH=AD=2,HG=AB=1,∴EH≠HG,故选项A错误;
∵E,F,G,H分别是AO,BO,CO,DO的中点,
∴EH=,
∴四边形EFGH是平行四边形,故选项B正确;
由题目中的条件,无法判断AC和BD是否垂直,故选项C错误;
∵点E、F分别为OA和OB的中点,
∴EF=,EF∥AB,∴△OEF∽△OAB,∴,
即△ABO的面积是△EFO的面积的4倍,故选项D错误,
故选B.
6. 【答案】D 【解析】∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴AB=BC=AC=2,∵四边形ABCD是菱形,∴∠AOB=90°,AO=AC=1,∴BO==,∴BD=2OB=2.
7. 【答案】C
8. 【答案】C
【解析】本题考查了矩形的性质,由勾股定理可得AC=10,再由矩形的对角线相等且互相平分的性质可得,OA=OD=5. △ABD的面积为24,OA为△ABD 的中线,由中线等分面积可得,△AOD的面积为12.再由等面积法即可得OE+EF的值.过程如下:
∵
∴ 即,∴OE+EF=,因此本题选C.
9. 【答案】A
【解析】正方形ABCD中,∵BC=4,
∴BC=CD=AD=4,∠BCE=∠CDF=90°,
∵AF=DE=1,∴DF=CE=3,∴BE=CF=5,
在△BCE和△CDF中,,
∴△BCE≌△CDF(SAS),∴∠CBE=∠DCF,
∵∠CBE+∠CEB=∠ECG+∠CEB=90°=∠CGE,
cos∠CBE=cos∠ECG=,
∴,CG=,∴GF=CF﹣CG=5﹣=,
故选A.
10. 【答案】B
【解析】本题考查了垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质,是常见问题的综合,灵活的运用所学知识是解答本题的关键.综合应用垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质等知识,逐个判断5个结论的正确性,得出结论.
①∵正方形ABCD,∴∠APE=∠AME=45°,∵PM⊥AE,∴∠AEP=∠AEM=90°,∵AE=AE,∴△APE≌△AME(ASA);
②过点N作NQ⊥AC于点Q,则四边形PNQE是矩形,∴PN=EQ,∵正方形ABCD,∴∠PAE=∠MAE=45°,∵PM⊥AE,∴∠PEA=45°,∴∠PAE=∠APE,PE=NQ,∴△APE等腰直角三角形,∴AE=PE,同理得:△NQC等腰直角三角形,∴NQ=CQ,∵△APE≌△AME,∴PE=ME,∴PE=ME= NQ=CQ,∴PM=AE+CQ,∴PM+PN=AE+CQ+EQ=AC,即PM+PN=AC成立;
③∵正方形ABCD,∴AC⊥BD,∴∠EOF是直角,∵过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,∴∠PEO和∠PFO是直角,∴四边形PFOE是矩形,∴PF=OE,在Rt△PEO中,有PE2+OE2=PO2,∴PE2+PF2=PO2,即PE2+PF2=PO2成立;
④△BNF是等腰直角三角形,点P不在AB的中点时,△POF不是等腰直角三角形,所以△POF与△BNF不一定相似,即△POF∽△BNF不一定成立;
⑤∵△AMP是等腰直角三角形,△PMN∽△AMP,∴△PMN是等腰直角三角形,∵∠MPN=90°,∴PM=PN,∵AP=PM,BP=PN,∴AP=BP,∴点P是AB的中点,又∵O为正方形的对称中点,∴点O在M、N两点的连线上.综上,①②③⑤成立,即正确的结论有4个,答案选B.
二、填空题(本大题共6道小题)
11. 【答案】1<a<7 【解析】如解图,对角线AC,BD相交于点O,则OA=AC=4,OD=BD=3,在△OAD中,OA-OD<AD<OA+OD,即1<a<7.
12. 【答案】
13. 【答案】
14. 【答案】
15. 【答案】①;②
16. 【答案】 【解析】∵四边形ABCD为正方形,∴AO=BO,∠AOF=∠BOE=90°,∵AM⊥BE,∠AFO=∠BFM,∴∠FAO=∠EBO,在△AFO和△BEO中,,∴△AFO≌△BEO(ASA),∴FO=EO,∵正方形ABCD的边长为2,E是OC的中点,∴FO=EO=1=BF,BO=2,∴在Rt△BOE中,BE==,由∠FBM=∠EBO,∠FMB=∠EOB,可得△BFM∽△BEO,∴=,即=,∴FM=.
三、解答题(本大题共5道小题)
17. 【答案】
延长交的延长线于,连结,
∵,,,
∴,∴是的中点.
∵,,∴.
在中,∵,
∴,又∵,
∴,又∴,
而,∴.
18. 【答案】
∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
∵BE=DF,∴△ABE≌△ADF,∴AE=CF.
19. 【答案】
证明:(1)∵AD∥EF,∴∠FEB=∠2.
∵∠1=∠2,∴∠FEB=∠1.∴BF=EF.∵BF=BC,
∴BC=EF.∴四边形BCEF是平行四边形.
∵BF=BC.∴四边形BCEF是菱形.
(2)∵EF=BC,AB=BC=CD,AD∥FE.
∴四边形ABEF、四边形CDEF均为平行四边形,
∴AF=BE,FC=ED.
又∵AC=2BC=BD.∴△ACF≌△BDE.
20. 【答案】
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,ABCD,OA=OC,
∴∠BAC=∠DCA,
又点M,N分别为、的中点,
∴,
在和中,
,
∴.
(2)BD=2BO,又已知BD=2AB,
∴BO=AB,∴△ABO为等腰三角形;
又M为AO的中点,
∴由等腰三角形的“三线合一”性质可知:BM⊥AO,
∴∠BMO=∠EMO=90°,
同理可证△DOC也为等腰三角形,
又N是OC的中点,
∴由等腰三角形的“三线合一”性质可知:DN⊥CO,
∠DNO=90°,
∵∠EMO+∠DNO=90°+90°=180°,
∴EMDN,
又已知EM=BM,由(1)中知BM=DN,
∴EM=DN,
∴四边形EMND平行四边形,
又∠EMO=90°,∴四边形EMND为矩形,
在Rt△ABM中,由勾股定理有:,
∴AM=CN=3,
∴MN=MO+ON=AM+CN=3+3=6,
∴.
21. 【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,
由折叠性质可知,∠D=∠AD′E=60°,
∴∠AD′E=∠B=60°,
∴ED′∥BC,
又∵EC∥D′B,
∴四边形BCED′是平行四边形,(4分)
∴ED′=BC=AD=1,
∴DE=ED′=1,
又DC=AB=2,
∴EC=1,
∴EC=ED′,
∴四边形BCED′是菱形.(6分)
(2)
解图
解:如解图所示,由折叠性质PD′=PD,BD之长即为所求,(8分)
作DG⊥BA的延长线于点G,
∵∠DAB=120°,
∴∠DAG=60°,
∵∠G=90°,
∴∠ADG=30°,
在Rt△ADG中,AD=1,
∴AG=,DG=,(9分)
∵AB=2,
∴BG=,
在Rt△BDG中,由勾股定理得:BD2=BG2+DG2=7,
∴BD=,
即PD′+PB的最小值为.(10分)
