人教版 八年级数学 第12章 全等三角形 综合训练 (word版 含解析)
文档属性
| 名称 | 人教版 八年级数学 第12章 全等三角形 综合训练 (word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 517.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 08:29:33 | ||
图片预览


文档简介
人教版 八年级数学 第12章 全等三角形 综合训练
一、选择题(本大题共10道小题)
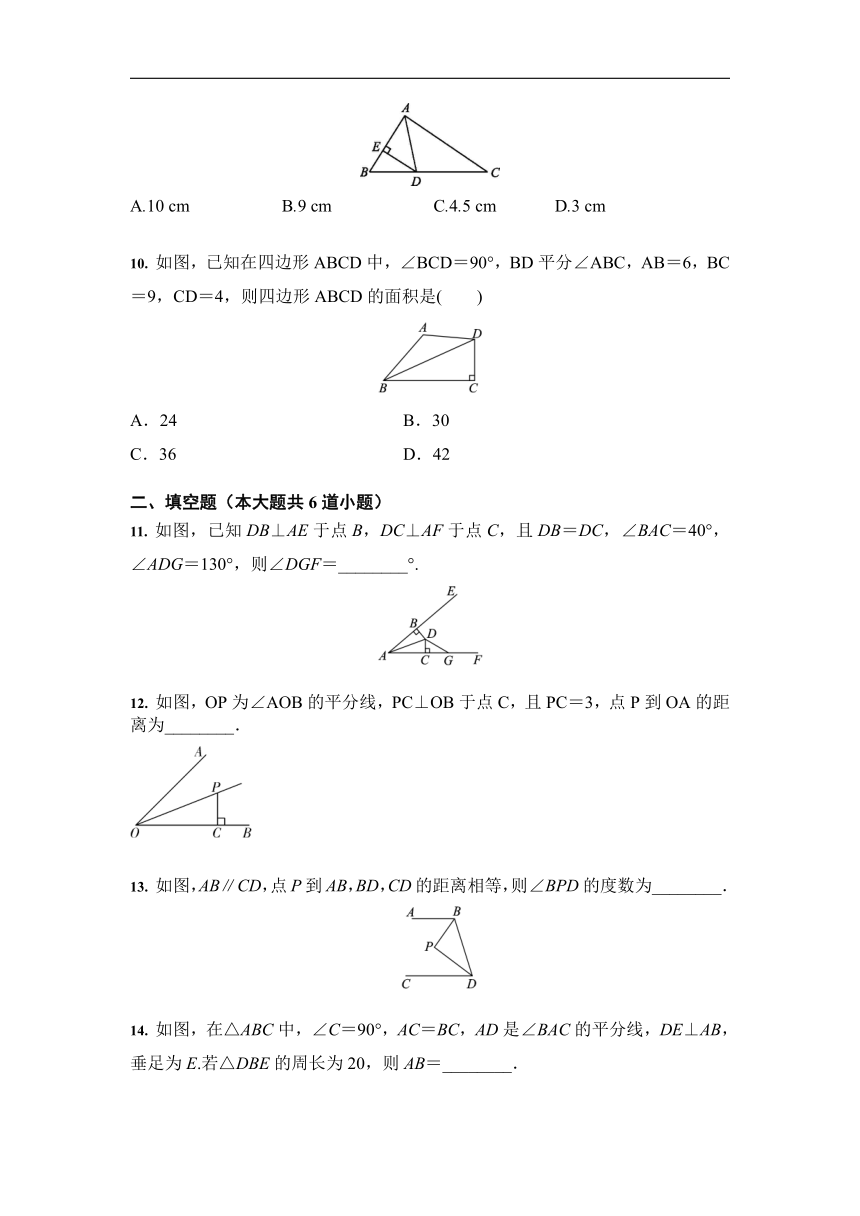
1. 如图,△ABC≌△A′B′C′,其中∠A=36°,∠C=24°,则∠B′的度数为( )
A.150° B.120° C.90° D.60°
2. 如图,已知∠1=∠2,欲证△ABD≌△ACD,还需从下列条件中补选一个,则错误的选项是( )
A.∠ADB=∠ADC B.∠B=∠C
C.DB=DC D.AB=AC
3. 如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是( )
A.∠A=∠C B.∠D=∠B
C.AD∥BC D.DF∥BE
4. 如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
5. 如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE B.AC=DF
C.∠A=∠D D.BF=EC
6. 如图,点B,E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是 ( )
A.BC=FD,AC=ED B.∠A=∠DEF,AC=ED
C.AC=ED,AB=EF D.∠A=∠DEF,BC=FD
7. 如图所示,△ABD≌△CDB,下列四个结论中,不正确的是( )
A.△ABD和△CDB的面积相等
B.△ABD和△CDB的周长相等
C.∠A+∠ABD=∠C+∠CBD
D.AD∥BC,AD=BC
8. 如图,△ACB≌△A'CB',∠ACA'=30°,则∠BCB'的度数为 ( )
A.20° B.30° C.35° D.40°
9. 如图,AD是△ABC的角平分线,DE⊥AB,AB=6 cm,DE=4 cm,S△ABC=30 cm2,则AC的长为( )
A.10 cm B.9 cm C.4.5 cm D.3 cm
10. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A.24 B.30
C.36 D.42
二、填空题(本大题共6道小题)
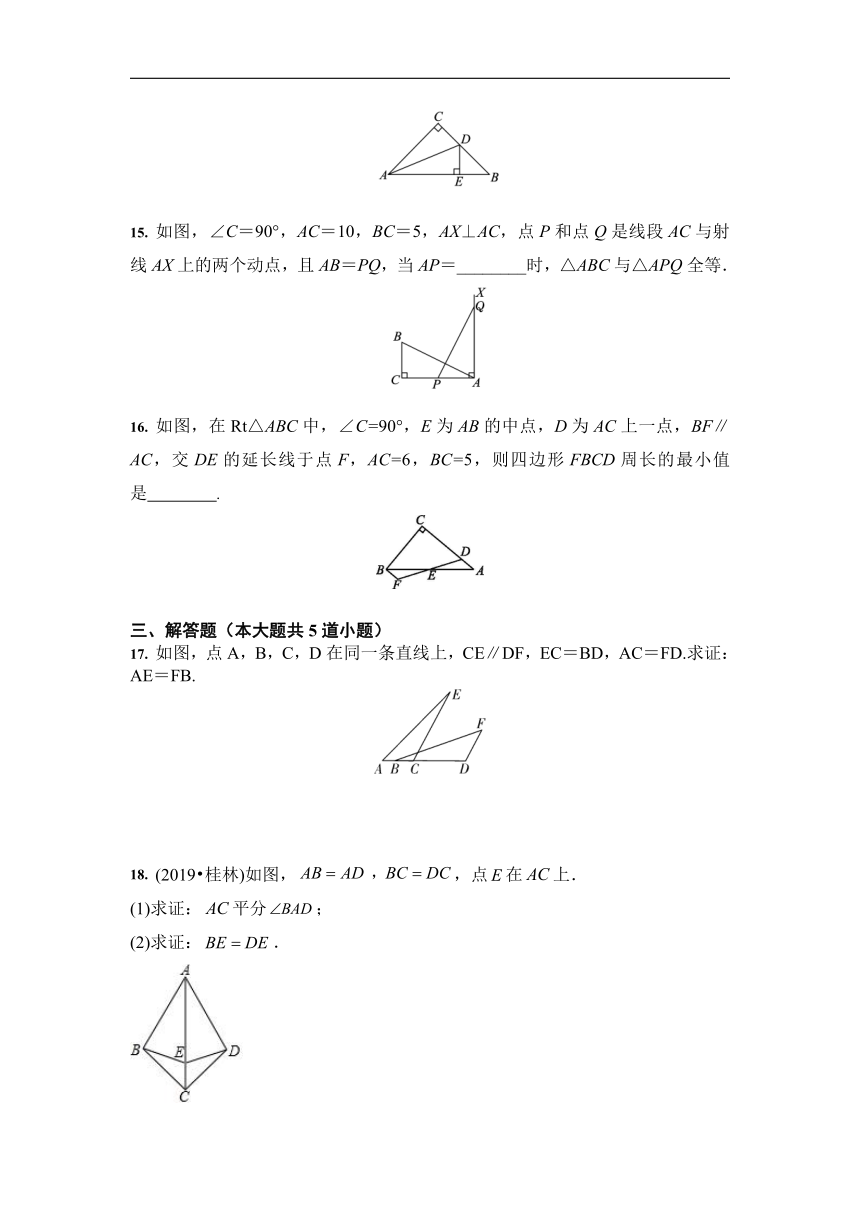
11. 如图,已知DB⊥AE于点B,DC⊥AF于点C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF=________°.
12. 如图,OP为∠AOB的平分线,PC⊥OB于点C,且PC=3,点P到OA的距离为________.
13. 如图,AB∥CD,点P到AB,BD,CD的距离相等,则∠BPD的度数为________.
14. 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.若△DBE的周长为20,则AB=________.
15. 如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q是线段AC与射线AX上的两个动点,且AB=PQ,当AP=________时,△ABC与△APQ全等.
16. 如图,在Rt△ABC中,∠C=90°,E为AB的中点,D为AC上一点,BF∥AC,交DE的延长线于点F,AC=6,BC=5,则四边形FBCD周长的最小值是 .
三、解答题(本大题共5道小题)
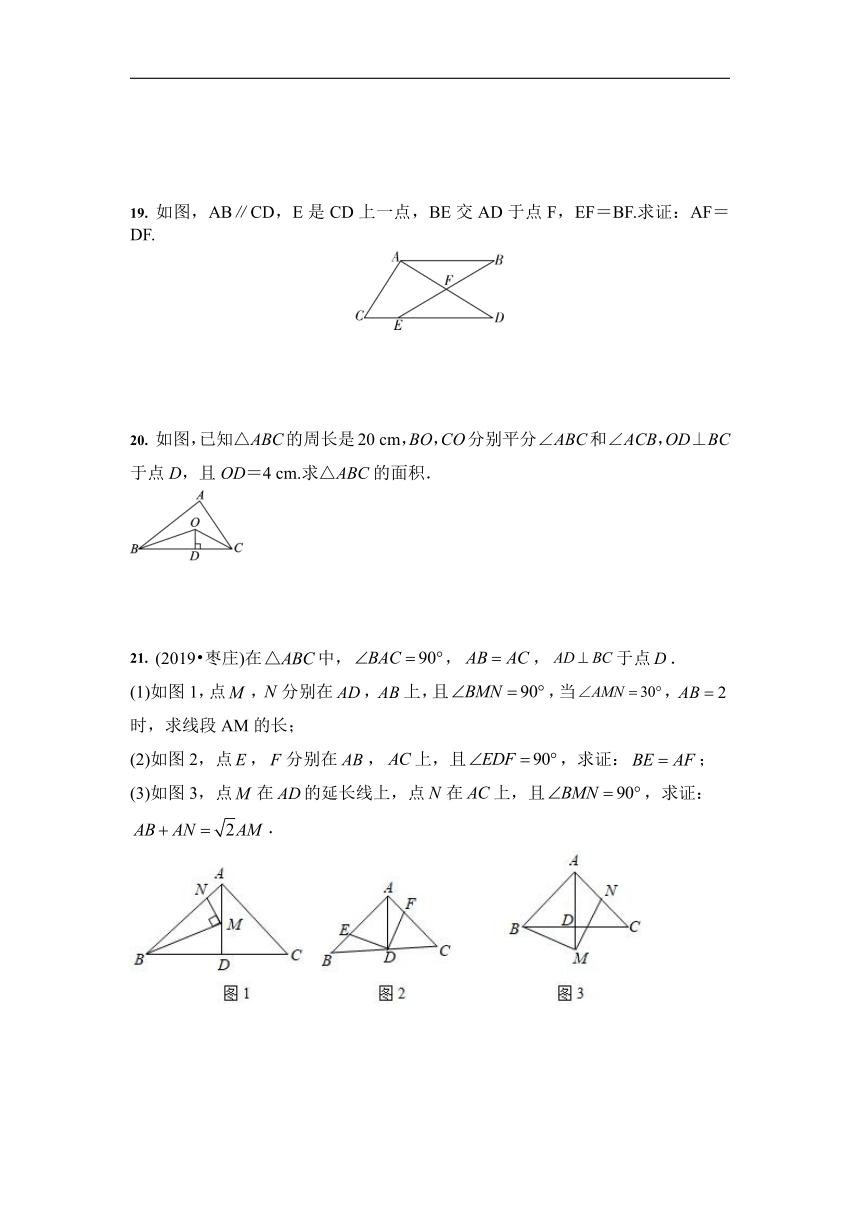
17. 如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.
18. (2019?桂林)如图,,点在上.
(1)求证:平分;
(2)求证:.
19. 如图,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF.求证:AF=DF.
20. 如图,已知△ABC的周长是20 cm,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=4 cm.求△ABC的面积.
21. (2019?枣庄)在中,,,于点.
(1)如图1,点,分别在,上,且,当,时,求线段AM的长;
(2)如图2,点,分别在,上,且,求证:;
(3)如图3,点在的延长线上,点在上,且,求证:.
人教版 八年级数学 第12章 全等三角形 综合训练-答案
一、选择题(本大题共10道小题)
1. 【答案】B [解析] ∵∠A=36°,∠C=24°,∴∠B=120°.∵△ABC≌△A′B′C′,
∴∠B=∠B′=120°.
2. 【答案】C [解析] 当添加条件A时,可用“ASA”证明△ABD≌△ACD;当添加条件B时,可用“AAS”证明△ABD≌△ACD;当添加条件D时,可用“SAS”证明△ABD≌△ACD;当添加条件C时,不能证明△ABD≌△ACD.
3. 【答案】B [解析] 在△ADF和△CBE中,由AD=BC,∠D=∠B,DF=BE,根据两边和它们的夹角分别相等的两个三角形全等,可以得到△ADF≌△CBE.故选B.
4. 【答案】C [解析] ①∵BE⊥AC,CF⊥AB,
∴∠CFB=∠BEC=90°.
在Rt△BCF和Rt△CBE中,
∴Rt△BCF≌Rt△CBE(HL).
②∵BE⊥AC,CF⊥AB,∴∠AFC=∠AEB=90°.在△ABE和△ACF中,
∴△ABE≌△ACF(AAS).
③设BE与CF相交于点O.
∵BE⊥AC,CF⊥AB,
∴∠OFB=∠OEC=90°.
∵△ABE≌△ACF,∴AB=AC,AE=AF.
∴BF=CE.
在△BOF和△COE中,
∴△BOF≌△COE(AAS).
5. 【答案】C [解析] 选项A中添加AB=DE可用“AAS”进行判定,故本选项不符合题意;
选项B中添加AC=DF可用“AAS”进行判定,故本选项不符合题意;
选项C中添加∠A=∠D不能判定△ABC≌△DEF,故本选项符合题意;
选项D中添加BF=EC可得出BC=EF,然后可用“ASA”进行判定,故本选项不符合题意.
故选C.
6. 【答案】C [解析] A.添加BC=FD,AC=ED,可利用“SAS”判定△ABC≌△EFD;
B.添加∠A=∠DEF,AC=ED,可利用“ASA”判定△ABC≌△EFD;
C.添加AC=ED,AB=EF,不能判定△ABC≌△EFD;
D.添加∠A=∠DEF,BC=FD,可利用“AAS”判定△ABC≌△EFD.
7. 【答案】C [解析] A.∵△ABD≌△CDB,
∴△ABD和△CDB的面积相等,故本选项不符合题意;
B.∵△ABD≌△CDB,
∴△ABD和△CDB的周长相等,故本选项不符合题意;
C.∵△ABD≌△CDB,
∴∠A=∠C,∠ABD=∠CDB.
∴∠A+∠ABD=∠C+∠CDB≠∠C+∠CBD,故本选项符合题意;
D.∵△ABD≌△CDB,
∴AD=BC,∠ADB=∠CBD.
∴AD∥BC,故本选项不符合题意.故选C.
8. 【答案】B [解析] 由△ACB≌△A'CB',得∠ACB=∠A'CB'.由等式的基本性质,得∠ACB-∠A'CB=
∠A'CB'-∠A'CB.所以∠BCB'=∠ACA'=30°.
9. 【答案】B [解析] 如图,过点D作DF⊥AC于点F.
∵AD是△ABC的角平分线,DE⊥AB,
∴DE=DF=4.
∵AB=6,
∴S△ABC=S△ABD+S△ACD=×6×4+AC×4=30,
解得AC=9(cm).故选B.
10. 【答案】B [解析] 过点D作DH⊥AB交BA的延长线于点H.
∵BD平分∠ABC,∠BCD=90°,
∴DH=CD=4.
∴四边形ABCD的面积=S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.
二、填空题(本大题共6道小题)
11. 【答案】150 [解析] ∵DB⊥AE于点B,DC⊥AF于点C,且DB=DC,
∴AD是∠BAC的平分线.
∵∠BAC=40°,∴∠CAD=∠BAC=20°.
∴∠DGF=∠CAD+∠ADG=20°+130°=150°.
12. 【答案】3 【解析】如解图,过点P作PD⊥OA于点D,∵OP为∠AOB的平分线,PC⊥OB于点C,∴PD=PC,∵PC=3,∴PD=3,即点P到点OA的距离为3.
13. 【答案】90° [解析] ∵点P到AB,BD,CD的距离相等,∴BP,DP分别平分∠ABD,∠BDC.
∵AB∥CD,∴∠ABD+∠BDC=180°.
∴∠PBD+∠PDB=90°.故∠BPD=90°.
14. 【答案】20 [解析] 由角平分线的性质可得CD=DE.易证Rt△ACD≌Rt△AED,则AC=AE,DE+DB=CD+DB=BC=AC=AE,故DE+DB+EB=AE+EB=AB.
15. 【答案】5或10 [解析] ∵AX⊥AC,∴∠PAQ=90°.∴∠C=∠PAQ=90°.
分两种情况:①当AP=BC=5时,
在Rt△ABC和Rt△QPA中,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=10时,
在Rt△ABC和Rt△PQA中,
∴Rt△ABC≌Rt△PQA(HL).
综上所述,当AP=5或10时,△ABC与△APQ全等.
16. 【答案】16 [解析] ∵BF∥AC,
∴∠EBF=∠EAD.
在△BFE和△ADE中,
∴△BFE≌△ADE(ASA).∴BF=AD.
∴BF+FD+CD+BC=AD+CD+FD+BC=AC+BC+FD=11+FD.
∵当FD⊥AC时,FD最短,此时FD=BC=5,
∴四边形FBCD周长的最小值为5+11=16.
三、解答题(本大题共5道小题)
17. 【答案】
证明:∵CE∥DF,
∴∠ACE=∠FDB,(2分)
在△ACE和△FDB中,,
∴△ACE≌△FDB(SAS),(5分)
∴AE=FB.(7分)
18. 【答案】
(1)在与中,,
∴,
∴,
即平分.
(2)由(1),
在与中,得,
∴,
∴.
19. 【答案】
证明:∵AB∥CD,
∴∠B=∠DEF,(1分)
在△AFB和△DFE中,
,(3分)
∴△AFB≌△DFE(ASA),(5分)
∴AF=DF.(6分)
20. 【答案】
解:∵BO,CO分别平分∠ABC和∠ACB,
∴点O到AB,AC,BC的距离相等.
∵△ABC的周长是20 cm,OD⊥BC于点D,且OD=4 cm,∴S△ABC=×20×4=40(cm2).
21. 【答案】
(1)∵,,,
∴,,,
∵,∴,
∵,∴,
∴,∴,
由勾股定理得,,即,解得,
∴.
(2)∵,,∴,
在和中,,
∴,
∴.
(3)如图,过点作交的延长线于,
∴,
则,,∴,
∵,,
∴,
在和中,,
∴,∴,
∴.
一、选择题(本大题共10道小题)
1. 如图,△ABC≌△A′B′C′,其中∠A=36°,∠C=24°,则∠B′的度数为( )
A.150° B.120° C.90° D.60°
2. 如图,已知∠1=∠2,欲证△ABD≌△ACD,还需从下列条件中补选一个,则错误的选项是( )
A.∠ADB=∠ADC B.∠B=∠C
C.DB=DC D.AB=AC
3. 如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是( )
A.∠A=∠C B.∠D=∠B
C.AD∥BC D.DF∥BE
4. 如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
5. 如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE B.AC=DF
C.∠A=∠D D.BF=EC
6. 如图,点B,E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是 ( )
A.BC=FD,AC=ED B.∠A=∠DEF,AC=ED
C.AC=ED,AB=EF D.∠A=∠DEF,BC=FD
7. 如图所示,△ABD≌△CDB,下列四个结论中,不正确的是( )
A.△ABD和△CDB的面积相等
B.△ABD和△CDB的周长相等
C.∠A+∠ABD=∠C+∠CBD
D.AD∥BC,AD=BC
8. 如图,△ACB≌△A'CB',∠ACA'=30°,则∠BCB'的度数为 ( )
A.20° B.30° C.35° D.40°
9. 如图,AD是△ABC的角平分线,DE⊥AB,AB=6 cm,DE=4 cm,S△ABC=30 cm2,则AC的长为( )
A.10 cm B.9 cm C.4.5 cm D.3 cm
10. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A.24 B.30
C.36 D.42
二、填空题(本大题共6道小题)
11. 如图,已知DB⊥AE于点B,DC⊥AF于点C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF=________°.
12. 如图,OP为∠AOB的平分线,PC⊥OB于点C,且PC=3,点P到OA的距离为________.
13. 如图,AB∥CD,点P到AB,BD,CD的距离相等,则∠BPD的度数为________.
14. 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.若△DBE的周长为20,则AB=________.
15. 如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q是线段AC与射线AX上的两个动点,且AB=PQ,当AP=________时,△ABC与△APQ全等.
16. 如图,在Rt△ABC中,∠C=90°,E为AB的中点,D为AC上一点,BF∥AC,交DE的延长线于点F,AC=6,BC=5,则四边形FBCD周长的最小值是 .
三、解答题(本大题共5道小题)
17. 如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.
18. (2019?桂林)如图,,点在上.
(1)求证:平分;
(2)求证:.
19. 如图,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF.求证:AF=DF.
20. 如图,已知△ABC的周长是20 cm,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=4 cm.求△ABC的面积.
21. (2019?枣庄)在中,,,于点.
(1)如图1,点,分别在,上,且,当,时,求线段AM的长;
(2)如图2,点,分别在,上,且,求证:;
(3)如图3,点在的延长线上,点在上,且,求证:.
人教版 八年级数学 第12章 全等三角形 综合训练-答案
一、选择题(本大题共10道小题)
1. 【答案】B [解析] ∵∠A=36°,∠C=24°,∴∠B=120°.∵△ABC≌△A′B′C′,
∴∠B=∠B′=120°.
2. 【答案】C [解析] 当添加条件A时,可用“ASA”证明△ABD≌△ACD;当添加条件B时,可用“AAS”证明△ABD≌△ACD;当添加条件D时,可用“SAS”证明△ABD≌△ACD;当添加条件C时,不能证明△ABD≌△ACD.
3. 【答案】B [解析] 在△ADF和△CBE中,由AD=BC,∠D=∠B,DF=BE,根据两边和它们的夹角分别相等的两个三角形全等,可以得到△ADF≌△CBE.故选B.
4. 【答案】C [解析] ①∵BE⊥AC,CF⊥AB,
∴∠CFB=∠BEC=90°.
在Rt△BCF和Rt△CBE中,
∴Rt△BCF≌Rt△CBE(HL).
②∵BE⊥AC,CF⊥AB,∴∠AFC=∠AEB=90°.在△ABE和△ACF中,
∴△ABE≌△ACF(AAS).
③设BE与CF相交于点O.
∵BE⊥AC,CF⊥AB,
∴∠OFB=∠OEC=90°.
∵△ABE≌△ACF,∴AB=AC,AE=AF.
∴BF=CE.
在△BOF和△COE中,
∴△BOF≌△COE(AAS).
5. 【答案】C [解析] 选项A中添加AB=DE可用“AAS”进行判定,故本选项不符合题意;
选项B中添加AC=DF可用“AAS”进行判定,故本选项不符合题意;
选项C中添加∠A=∠D不能判定△ABC≌△DEF,故本选项符合题意;
选项D中添加BF=EC可得出BC=EF,然后可用“ASA”进行判定,故本选项不符合题意.
故选C.
6. 【答案】C [解析] A.添加BC=FD,AC=ED,可利用“SAS”判定△ABC≌△EFD;
B.添加∠A=∠DEF,AC=ED,可利用“ASA”判定△ABC≌△EFD;
C.添加AC=ED,AB=EF,不能判定△ABC≌△EFD;
D.添加∠A=∠DEF,BC=FD,可利用“AAS”判定△ABC≌△EFD.
7. 【答案】C [解析] A.∵△ABD≌△CDB,
∴△ABD和△CDB的面积相等,故本选项不符合题意;
B.∵△ABD≌△CDB,
∴△ABD和△CDB的周长相等,故本选项不符合题意;
C.∵△ABD≌△CDB,
∴∠A=∠C,∠ABD=∠CDB.
∴∠A+∠ABD=∠C+∠CDB≠∠C+∠CBD,故本选项符合题意;
D.∵△ABD≌△CDB,
∴AD=BC,∠ADB=∠CBD.
∴AD∥BC,故本选项不符合题意.故选C.
8. 【答案】B [解析] 由△ACB≌△A'CB',得∠ACB=∠A'CB'.由等式的基本性质,得∠ACB-∠A'CB=
∠A'CB'-∠A'CB.所以∠BCB'=∠ACA'=30°.
9. 【答案】B [解析] 如图,过点D作DF⊥AC于点F.
∵AD是△ABC的角平分线,DE⊥AB,
∴DE=DF=4.
∵AB=6,
∴S△ABC=S△ABD+S△ACD=×6×4+AC×4=30,
解得AC=9(cm).故选B.
10. 【答案】B [解析] 过点D作DH⊥AB交BA的延长线于点H.
∵BD平分∠ABC,∠BCD=90°,
∴DH=CD=4.
∴四边形ABCD的面积=S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.
二、填空题(本大题共6道小题)
11. 【答案】150 [解析] ∵DB⊥AE于点B,DC⊥AF于点C,且DB=DC,
∴AD是∠BAC的平分线.
∵∠BAC=40°,∴∠CAD=∠BAC=20°.
∴∠DGF=∠CAD+∠ADG=20°+130°=150°.
12. 【答案】3 【解析】如解图,过点P作PD⊥OA于点D,∵OP为∠AOB的平分线,PC⊥OB于点C,∴PD=PC,∵PC=3,∴PD=3,即点P到点OA的距离为3.
13. 【答案】90° [解析] ∵点P到AB,BD,CD的距离相等,∴BP,DP分别平分∠ABD,∠BDC.
∵AB∥CD,∴∠ABD+∠BDC=180°.
∴∠PBD+∠PDB=90°.故∠BPD=90°.
14. 【答案】20 [解析] 由角平分线的性质可得CD=DE.易证Rt△ACD≌Rt△AED,则AC=AE,DE+DB=CD+DB=BC=AC=AE,故DE+DB+EB=AE+EB=AB.
15. 【答案】5或10 [解析] ∵AX⊥AC,∴∠PAQ=90°.∴∠C=∠PAQ=90°.
分两种情况:①当AP=BC=5时,
在Rt△ABC和Rt△QPA中,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=10时,
在Rt△ABC和Rt△PQA中,
∴Rt△ABC≌Rt△PQA(HL).
综上所述,当AP=5或10时,△ABC与△APQ全等.
16. 【答案】16 [解析] ∵BF∥AC,
∴∠EBF=∠EAD.
在△BFE和△ADE中,
∴△BFE≌△ADE(ASA).∴BF=AD.
∴BF+FD+CD+BC=AD+CD+FD+BC=AC+BC+FD=11+FD.
∵当FD⊥AC时,FD最短,此时FD=BC=5,
∴四边形FBCD周长的最小值为5+11=16.
三、解答题(本大题共5道小题)
17. 【答案】
证明:∵CE∥DF,
∴∠ACE=∠FDB,(2分)
在△ACE和△FDB中,,
∴△ACE≌△FDB(SAS),(5分)
∴AE=FB.(7分)
18. 【答案】
(1)在与中,,
∴,
∴,
即平分.
(2)由(1),
在与中,得,
∴,
∴.
19. 【答案】
证明:∵AB∥CD,
∴∠B=∠DEF,(1分)
在△AFB和△DFE中,
,(3分)
∴△AFB≌△DFE(ASA),(5分)
∴AF=DF.(6分)
20. 【答案】
解:∵BO,CO分别平分∠ABC和∠ACB,
∴点O到AB,AC,BC的距离相等.
∵△ABC的周长是20 cm,OD⊥BC于点D,且OD=4 cm,∴S△ABC=×20×4=40(cm2).
21. 【答案】
(1)∵,,,
∴,,,
∵,∴,
∵,∴,
∴,∴,
由勾股定理得,,即,解得,
∴.
(2)∵,,∴,
在和中,,
∴,
∴.
(3)如图,过点作交的延长线于,
∴,
则,,∴,
∵,,
∴,
在和中,,
∴,∴,
∴.
