力的分解

(共25张PPT)
第三章 相互作用
5、力的分解
复习：
1.分力与合力
2.力的合成
3.力的合成遵循平行四边形定则
上节知识要点：
既然我们已知道力的合成的方法，那么已知一个力求它的分力，该怎么做呢？
提问：
一、力的分解的定义
已知一个力求它的分力的过程,叫做力的分解
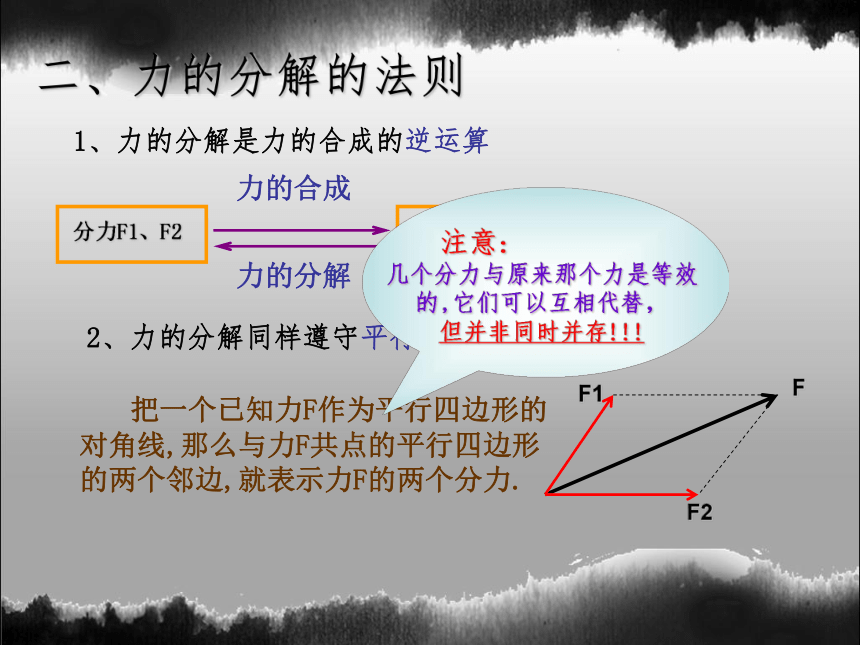
二、力的分解的法则
1、力的分解是力的合成的逆运算
2、力的分解同样遵守平行四边行定则
把一个已知力F作为平行四边形的对角线,那么与力F共点的平行四边形的两个邻边,就表示力F的两个分力.
分力F1、F2
合力F
力的合成
力的分解
注意:
几个分力与原来那个力是等效的,它们可以互相代替，
但并非同时并存!!!
F
F1
F2
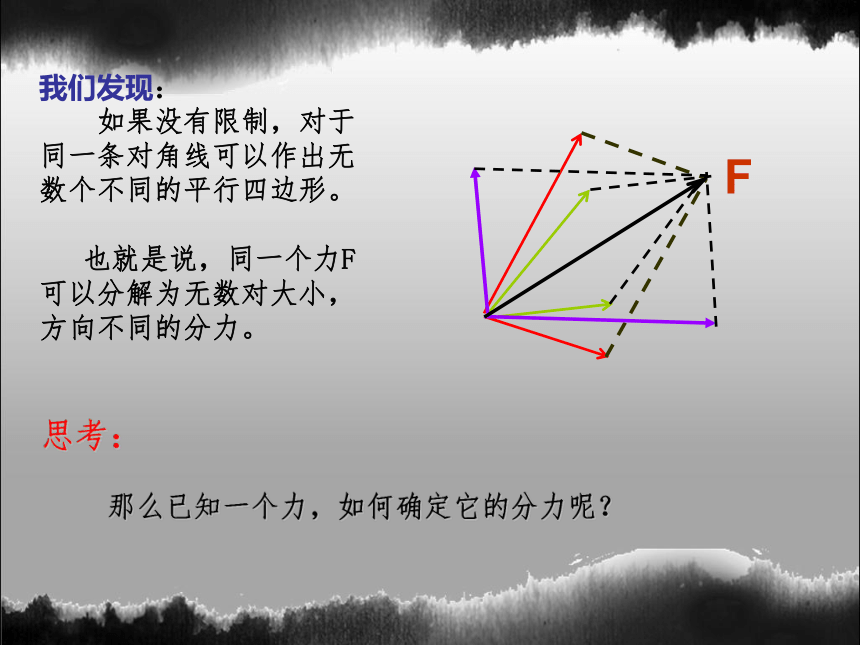
我们发现：
如果没有限制，对于同一条对角线可以作出无数个不同的平行四边形。
也就是说，同一个力F可以分解为无数对大小，方向不同的分力。
F
那么已知一个力，如何确定它的分力呢？
思考：
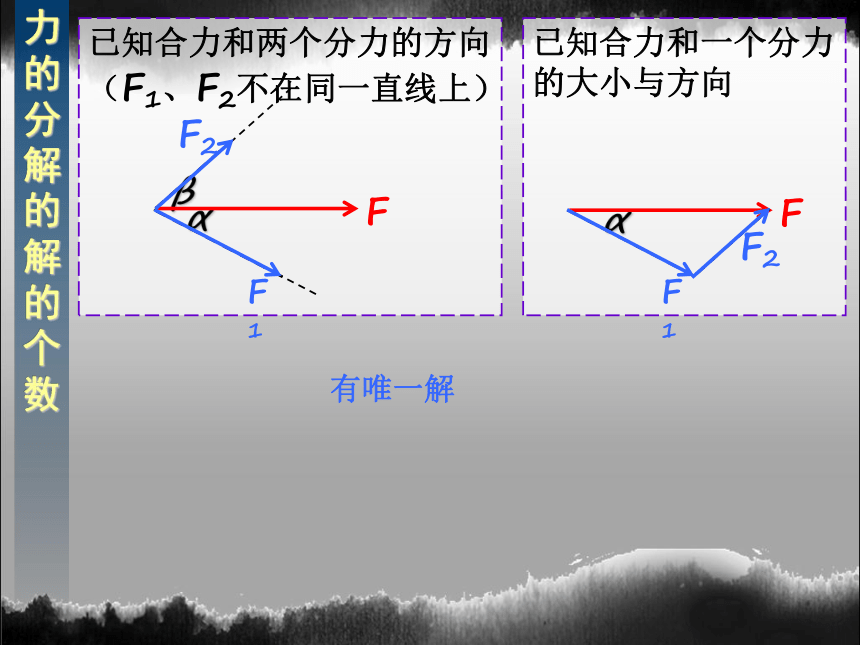
已知合力和两个分力的方向（F1、F2不在同一直线上）
α
β
F
F2
F1
已知合力和一个分力的大小与方向
α
F1
F
力的分解的解的个数
F2
有唯一解
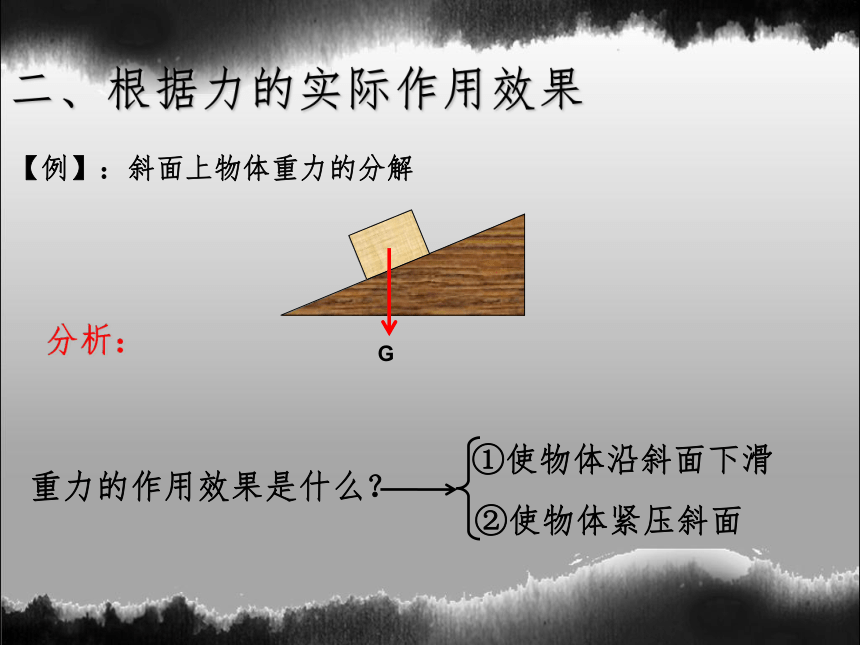
二、根据力的实际作用效果
【例】：斜面上物体重力的分解
①使物体沿斜面下滑
②使物体紧压斜面
重力的作用效果是什么？
G
分析：
由公式可以看出,F1和F2的大小只与倾角θ的大小有关:
θ
θ
θ
F1
F2
F1
F2
如图建立直角坐标系，将G分解到x轴和y轴上，F1，F2即重力沿两个方向的分力：
F1=G·sinθ
F2=G·cosθ
G
F1
F2
x
y
结论：
F
G
G
G
F
a
b
F
大桥为什么要建很长的引桥？
为了减小倾角，以减小重力在沿斜面的分力，以便汽车爬坡。
当θ较大时，G1较大车辆上坡艰难而下坡又不安全，为了行车方便与安全，高大的桥要建造很长的引桥来减小桥面的坡度θ
滑梯的倾角θ较大，滑梯上的小孩儿就容易下滑
为什么滑梯的倾角往往设计得比较大？
F1
F2
F
O
练习一：
钩码对O点拉力产生的效果，再对 分解
F
F
四两拨千斤
泥潭拔车
F1
F2
生活中力的分解例子
F
F1
F2
若将斧头磨锋利之后
磨刀不误砍柴工
F
F1
F2
例3：斧子劈开木桩
【例题】：一个大人拉着载有两个小孩的小车匀速前进。大人的拉力为135N，拉杆与水平地面成 θ ＝53°，问使小车前进的动力有多大？
解：大小：F1=F·cosθ=135×cos53°=135×0.6=81N
θ
方向：水平向前
y
x
O
F
F1
＊三角形定则
平行四边形定则
F1
F2
F
F1
F2
F
三角形定则
F1
F2
F
或
三角形定则
两个矢量首尾相接，从第一个矢量的始端指向第二个矢量的末端的有向线段就表示合矢量的大小和方向.
三角形定则与平行四边形定则实质一样．
C
B
A
注：一般情况下，矢量可以平移
矢量和标量的再认识
矢量：①既有大小，又有方向，
②相加时，遵从平 行四边形定则。
如：力、位移、速度、加速度等
标量：①只有大小，没有方向，
②求和时按照代数相加。
如：质量、时间、路程、速率等
力的分解方法小结
实际问题
力的作用效果
确定两分力方向
作平行四边形
用数学知识解
力的分解定则
思路点播
五、课堂小结
1、力的合成与分解都遵循平行四边形定则。
2、求一个已知力的两个分力的任意解是无数的。
3、实际应用中，分解一个力，常根据这个力的实际
作用效果来确定分力的方向。再由几何关系求两
个分力的大小。
【例题2】已知重力G，求在下列两种情况下重力G
的两个分力
θ
θ
G
G
F1
F2
F1
F2
G1 = G· tanθ
G2 = G/ cosθ
G1 = G· sinθ
G2 = G·cosθ
G1
G2
θ
G1
G2
θ
M
G
T1
T2
O
N
370
530
T
例3、把一物体挂在互成角度的两根细绳MO，NO上，已知物体对悬点O的拉力T等于物体所受的重力G。如图所示，怎样把力T按其作用效果分解 它的两个分力的大小、方向如何？
（sin370=0.6, cos370=0.8)
370