青岛版数学八年级下册课件:10.3一次函数的性质(共44张PPT)
文档属性
| 名称 | 青岛版数学八年级下册课件:10.3一次函数的性质(共44张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 537.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 00:00:00 | ||
图片预览






文档简介
(共44张PPT)
一次函数的性质
1.作函数图像的步骤是什么?
(1)列表
(2)描点
(3)连线
2.一次函数图像的特点是什么?
是一条直线,所以我们在作一次图像的时候只需要确定两个点,再过这两个点作直线就可以了。
知识回顾
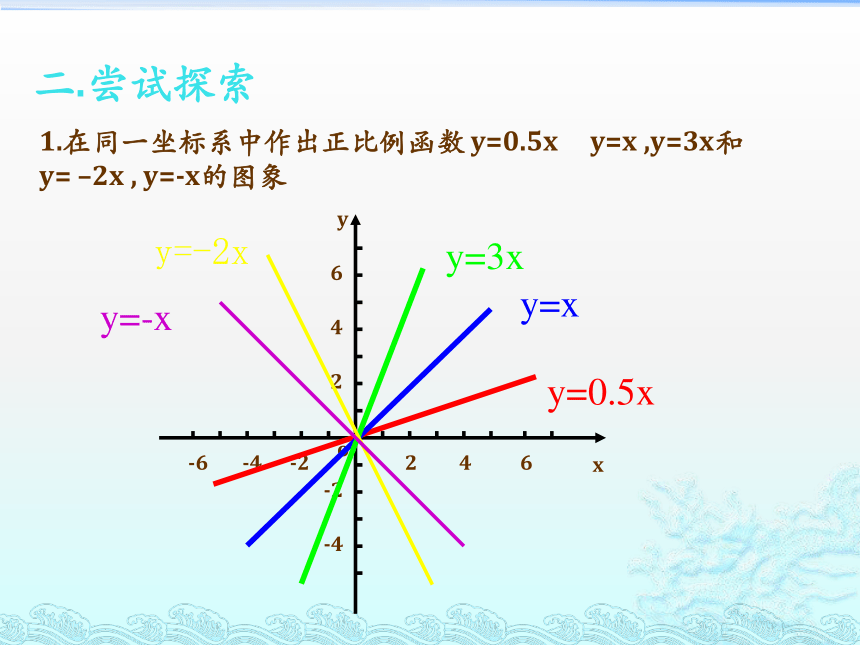
二.尝试探索
1.在同一坐标系中作出正比例函数
y=0.5x
y=x
,y=3x和
y=
–2x
,
y=-x的图象
-6
o
-4
4
6
2
4
6
-2
-2
-4
x
y
2
y=0.5x
y=x
y=3x
y=-2x
y=-x
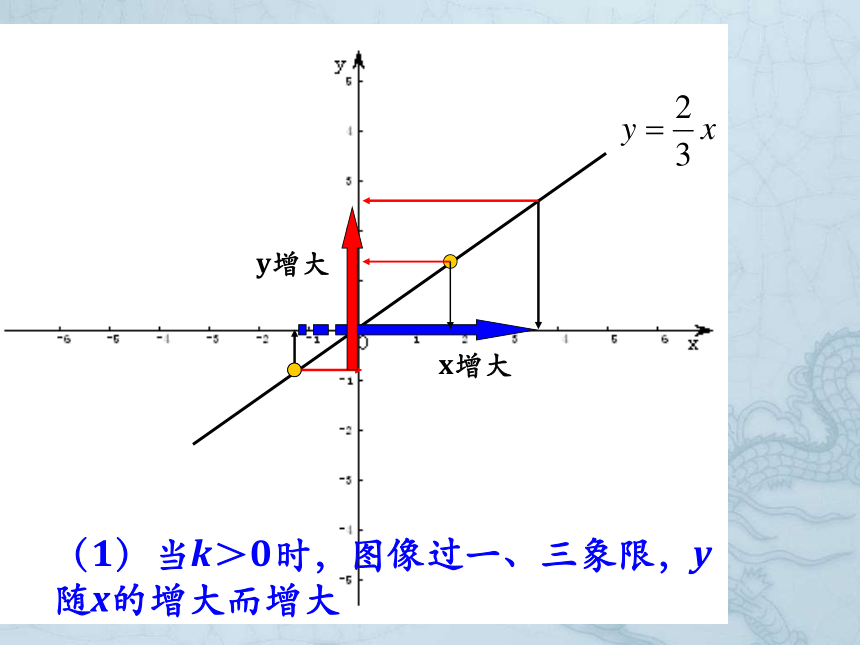
x增大
y增大
(1)当k>0时,图像过一、三象限,y随x的增大而增大
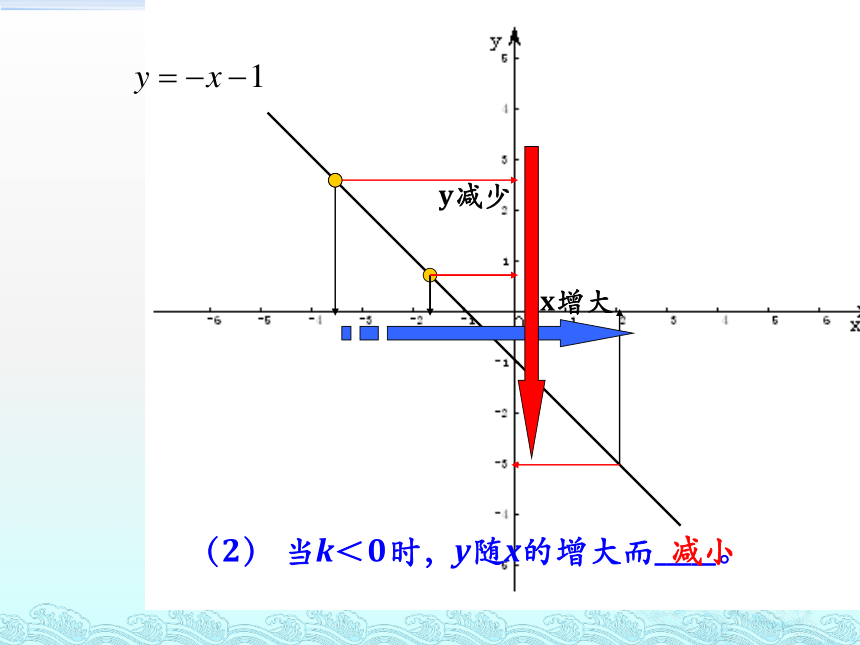
x增大
y减少
(2)
当k<0时,图像过二、四象限,y随x的增大而_____。
减小
PPT模板:www.1ppt.com/moban/
PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/
PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/
PPT教程:
www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/
范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/
教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn
PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/
数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/
美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/
物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/
生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/
历史课件:www.1ppt.com/kejian/lishi/
-6
o
-4
4
6
2
4
6
-2
-2
-4
x
y
2
y=0.5x
y=x
y=3x
y=-2x
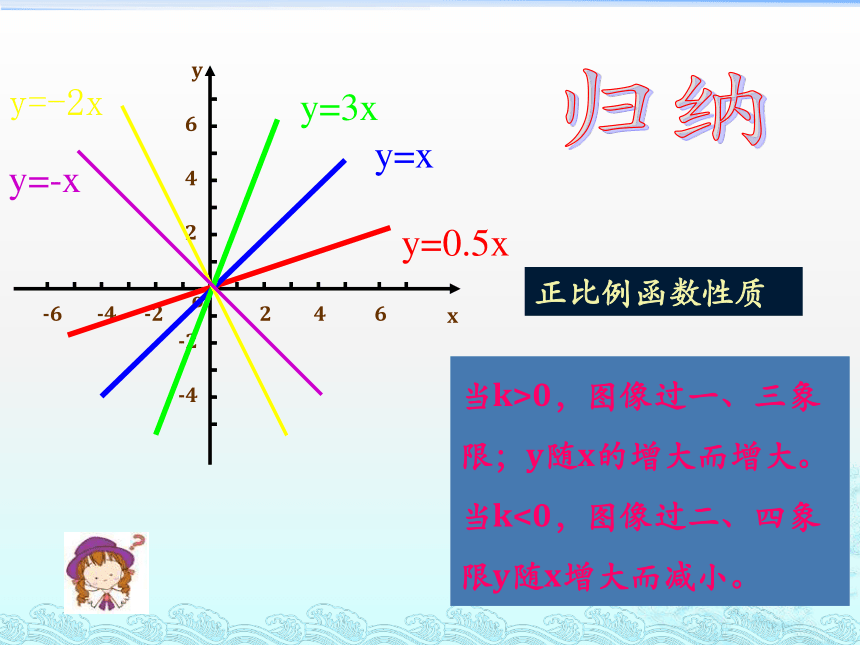
正比例函数性质
当k>0,图像过一、三象限;y随x的增大而增大。
当k<0,图像过二、四象限y随x增大而减小。
y=-x
归纳
随堂练习
2.正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是(
)
A.m=1
B.m>1
C.m<1
D、m≥1
B
1.函数y=-7x的图象在第
象限内,
y随x的增大而
.
二、四
减小
3.正比例函数y=(3-k)
x,如果随着x的增大y反而减小,则k的取值范围是
.
k>3
4
.若正比例函数图像又y=(3k-6)x的图像经过点A(x1,x2)和B(y1,y2),当x1y1>y2,则k的取值范围是
(
)
A.k>2
B.k<2
C.k=2
D.无法确定
5.在函数y=kx(k>0)的图像上有三个点A1(x1,y1)、
A2(x2,y2)、
已知x1用“<”将y1、y2连接起来
。
B
y1x增大
y增大
(1)当k>0时,y随x的增大而增大
x增大
y减少
(2)
当k<0时,y随x的增大而_____。
减小
一次函数y=kx+b有下列性质:
?(1)
当k>0时,y随x的增大而_____
;
?(2)
当k<0时,y随x的增大而_____。
概括
减小
增大
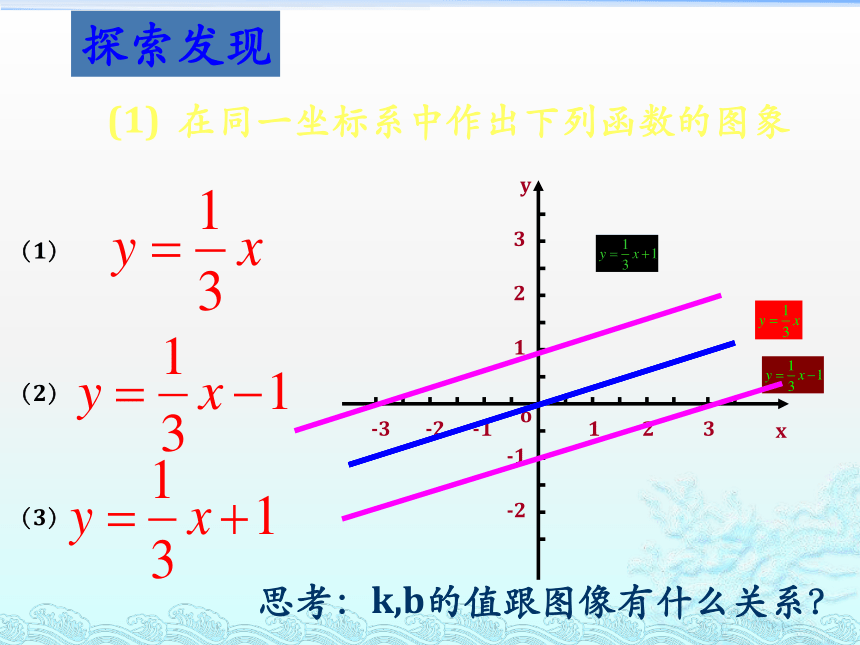
探索发现
(1)
在同一坐标系中作出下列函数的图象
(1)
(2)
(3)
-3
o
-2
2
3
1
2
3
-1
-1
-2
x
y
1
思考:k,b的值跟图像有什么关系?
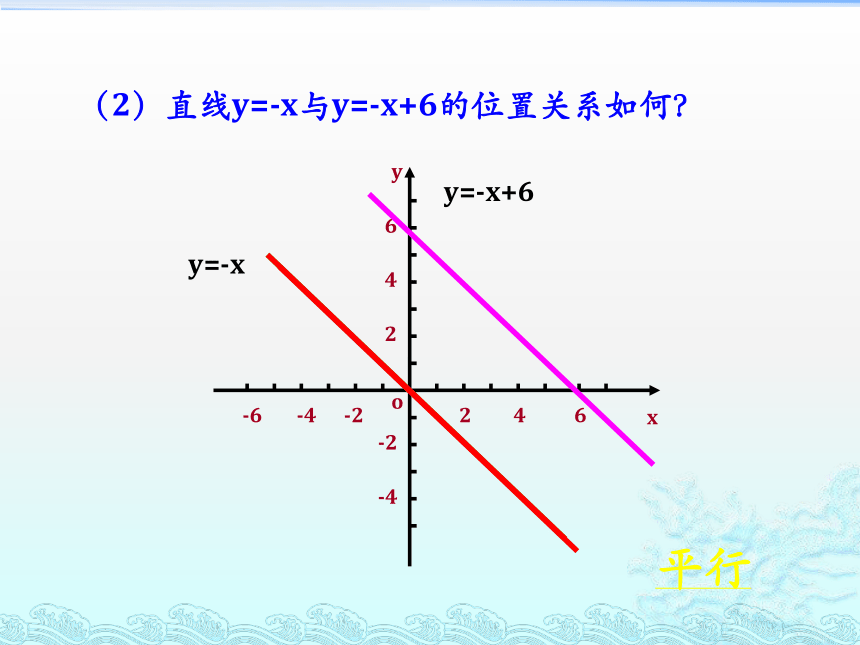
(2)直线y=-x与y=-x+6的位置关系如何?
-6
o
-4
4
6
2
4
6
-2
-2
-4
x
y
2
y=-x+6
y=-x
平行
-
(2)在同一坐标系中作出下列函数的图象
(1)
(2)
(3)
-3
o
-2
2
3
1
2
3
-1
-1
-2
x
y
1
思考
结论
K>o
b=0
b>0
b<0
b=0
b>0
b<0
通过作以上一次函数的图像我们发现y=kx+b
中,k,b的取值跟图像的关系如下:
K<0
一,三
一,二,三
一,三,四
二,四
一,二,四
二,三,四
当k>0时,y的值随x的增大而增大
当k<0时,y的值随x的增大而减小
(3)
小试牛刀
1在平面直角坐标系中,函数y=-2x+3的图象经过(
)
A.一、二、三象限
B.二、三、四象限
C.一、三、四象限
D.一、二、四象限
2已知一次函数y=x-2的大致图像为
(
)
A
B
C
D
D
C
1.下列函数中,y的值随x值的增大而增大的函数是________.
A.y=-2x
B.y=-2x+1
C.y=x-2
D.y=-x-2
课堂练习:
C
课堂练习:
2、直线y=3x-2可由直线y=3x向
平移
个单位得到。
下
2
课堂练习:
3、直线y=x+2可由直线y=x-1向______平移_______个单位得到。
上
3
4、确定y=kx+b中k,b的符号
k
>
0
b
>
0
(1)
k
<
0
b
<0
(2)
4、确定y=kx+b中k,b的符号
(3)
O
y
x
k
>
0
b
<
0
4、确定y=kx+b中k,b的符号
(4)
O
y
x
k
<
0
b
>
0
4、确定y=kx+b中k,b的符号
5、直线y=kx+b不经过第四象限,判断k,b的符号
k
>
0
b
≥0
b
>0
(1)对于函数y=-5+6x,
y的值随x的值增大而
__________
增大
填空
(2)函数y=2x-1的图
象不经过第
象限
二
填空
(3)对于函数y=5x+6,
y随x的减小而_____
减小
填空
(4)函数y=2x-1
经过
象限。
一、三、四
填空
练一练
1、下列一次函数中,y的值随x的增大而减小
的有________
(2)、(4)
2、函数
的共同性质是(
)
A
它们的图象都不经过第二象限
B
它们的图象都不经过原点
C
函数y都随自变量x的增大而增大
D
函数y都随自变量x的增大而减小
D
3.下列哪个图像是一次函数y=-3x+5
和y=2x-4的大致图像( )
(A)
(B)
(C)
(D)
B
历史使人聪明,诗歌使人机智,数学使人精细。
1、有下列函数:①y=2x+1,
②y=-3x+4,
③
y=0.5x,
④y=x-6;
①③④
②
③
①
函数y随x的增大而增大的是__________;
其中过原点的直线是________;
函数y随x的增大而减小的是___________;
图象在第一、二、三象限的是________
。
练一练
2、根据下列一次函数y=kx+b(k
≠
0)的草图回答出各图中k、b的符号:
k___0,b___0
k___0,b___0
k___0,b___0
k___0,b___0
>
<
>
>
>
<
<
<
经过一,二,三象限
经过一,三四象限
经过一,二,四象限
经过二,三,四象限
y
x
0
(D)
y
x
0
(A
)
y
x
0
(
C
)
y
x
0
(B)
小试牛刀
3、已知函数
y
=
kx的图象在二、四象限,那么函数y
=
kx-k的图象可能是(
)
B
例1
、已知函数y=(m+2)x+
(1)当m取何值时,y随x的增大而增大?
这时它的图象经过哪些象限?
(2)当
m取何值时,y随x的增大而减小?
这时它的图象经过哪些象限?
例2、
已知一次函数y=kx-k,且y随x的增大而增大,试判断它的图象经过哪几个象限?
拓展与应用
1、一次函数y=kx+b中,kb>0,且y随x的增大而
减小,则它的图象大致为(
)
2.
写出m的3个值,使相应的一次函数
y
=
(2m-1)x+2的值都是随x的增大而增大
C
3.如果一次函数y=kx-3k+6的图象经
过原点,那么k的值为_________。
4.写出m的3个值,使相应的一次函数
y
=
(2m-1)x+2的值都是随x的增大而减小.
K=2
可以写无数个,只要满足2m-1<0就可以了。
例如:m=0.m=-1,m=-2
小结:
本节课的主要内容有:
1.正比例函数的特点是什么?
2.一次函数及其图像的性质有哪些?
3.函数图像的位置关系有几种?
4.关于函数y=kx+b图像的大致
位置跟k,b的关系。
例1
在同一平面直角坐标系中画出下列每组函数的图象:
一次函数y=kx+b(k≠0)
图象的画法
(两点)
比较下列一对一次函数的图象有什么共同点,
有什么不同点?
K相同
b不同
K相同
b不同
直线(图象)平行
直线(图象)平行
对于直线y=k1x+b1与直线
y=k2x+b2
当k1=k2
,
b1≠b2
时,两直线平行
;
K不同
b相同
直线(图象)相交
当k1
≠
k2
,
b1=b2
时,两直线相交于点(0,b)
;
画出一次函数
的图象
3
1
y
3
0
X
观察分析:
当一个点在直线上从左向右移动时,它的位置怎样变化
自变量x由___到___
函数y的值从___到___
大
小
小
大
画出一次函数
的图象
3
1
y
3
0
X
观察分析:
自变量x由___到___
函数y的值从___到___
大
小
小
大
函数y=3x-2的图象是否也有这种现象
当k>0时,y随x的增大而增大,
结论
的图象
观察分析:
自变量x由___到___
函数y的值从___到___
大
小
小
大
当k<0时,y随x的增大而减小,
结论
五.想一想
1)x从0开始逐渐增
大时,y=2x+6和y=5x
哪一个的值先达到20?
这说明了什么?
-15
o
-10
10
15
5
10
15
-5
-5
-10
x
20
5
y
y=5x
y=2x+6
你看出来了吗?
(3)直线y=2x+6与y=-x+6的位置关系如何?
-6
o
-4
4
6
2
4
6
-2
-2
-4
x
y
2
y=-x+6
y=2x+6
相交
一次函数的性质
1.作函数图像的步骤是什么?
(1)列表
(2)描点
(3)连线
2.一次函数图像的特点是什么?
是一条直线,所以我们在作一次图像的时候只需要确定两个点,再过这两个点作直线就可以了。
知识回顾
二.尝试探索
1.在同一坐标系中作出正比例函数
y=0.5x
y=x
,y=3x和
y=
–2x
,
y=-x的图象
-6
o
-4
4
6
2
4
6
-2
-2
-4
x
y
2
y=0.5x
y=x
y=3x
y=-2x
y=-x
x增大
y增大
(1)当k>0时,图像过一、三象限,y随x的增大而增大
x增大
y减少
(2)
当k<0时,图像过二、四象限,y随x的增大而_____。
减小
PPT模板:www.1ppt.com/moban/
PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/
PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/
PPT教程:
www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/
范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/
教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn
PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/
数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/
美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/
物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/
生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/
历史课件:www.1ppt.com/kejian/lishi/
-6
o
-4
4
6
2
4
6
-2
-2
-4
x
y
2
y=0.5x
y=x
y=3x
y=-2x
正比例函数性质
当k>0,图像过一、三象限;y随x的增大而增大。
当k<0,图像过二、四象限y随x增大而减小。
y=-x
归纳
随堂练习
2.正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是(
)
A.m=1
B.m>1
C.m<1
D、m≥1
B
1.函数y=-7x的图象在第
象限内,
y随x的增大而
.
二、四
减小
3.正比例函数y=(3-k)
x,如果随着x的增大y反而减小,则k的取值范围是
.
k>3
4
.若正比例函数图像又y=(3k-6)x的图像经过点A(x1,x2)和B(y1,y2),当x1
(
)
A.k>2
B.k<2
C.k=2
D.无法确定
5.在函数y=kx(k>0)的图像上有三个点A1(x1,y1)、
A2(x2,y2)、
已知x1
。
B
y1
y增大
(1)当k>0时,y随x的增大而增大
x增大
y减少
(2)
当k<0时,y随x的增大而_____。
减小
一次函数y=kx+b有下列性质:
?(1)
当k>0时,y随x的增大而_____
;
?(2)
当k<0时,y随x的增大而_____。
概括
减小
增大
探索发现
(1)
在同一坐标系中作出下列函数的图象
(1)
(2)
(3)
-3
o
-2
2
3
1
2
3
-1
-1
-2
x
y
1
思考:k,b的值跟图像有什么关系?
(2)直线y=-x与y=-x+6的位置关系如何?
-6
o
-4
4
6
2
4
6
-2
-2
-4
x
y
2
y=-x+6
y=-x
平行
-
(2)在同一坐标系中作出下列函数的图象
(1)
(2)
(3)
-3
o
-2
2
3
1
2
3
-1
-1
-2
x
y
1
思考
结论
K>o
b=0
b>0
b<0
b=0
b>0
b<0
通过作以上一次函数的图像我们发现y=kx+b
中,k,b的取值跟图像的关系如下:
K<0
一,三
一,二,三
一,三,四
二,四
一,二,四
二,三,四
当k>0时,y的值随x的增大而增大
当k<0时,y的值随x的增大而减小
(3)
小试牛刀
1在平面直角坐标系中,函数y=-2x+3的图象经过(
)
A.一、二、三象限
B.二、三、四象限
C.一、三、四象限
D.一、二、四象限
2已知一次函数y=x-2的大致图像为
(
)
A
B
C
D
D
C
1.下列函数中,y的值随x值的增大而增大的函数是________.
A.y=-2x
B.y=-2x+1
C.y=x-2
D.y=-x-2
课堂练习:
C
课堂练习:
2、直线y=3x-2可由直线y=3x向
平移
个单位得到。
下
2
课堂练习:
3、直线y=x+2可由直线y=x-1向______平移_______个单位得到。
上
3
4、确定y=kx+b中k,b的符号
k
>
0
b
>
0
(1)
k
<
0
b
<0
(2)
4、确定y=kx+b中k,b的符号
(3)
O
y
x
k
>
0
b
<
0
4、确定y=kx+b中k,b的符号
(4)
O
y
x
k
<
0
b
>
0
4、确定y=kx+b中k,b的符号
5、直线y=kx+b不经过第四象限,判断k,b的符号
k
>
0
b
≥0
b
>0
(1)对于函数y=-5+6x,
y的值随x的值增大而
__________
增大
填空
(2)函数y=2x-1的图
象不经过第
象限
二
填空
(3)对于函数y=5x+6,
y随x的减小而_____
减小
填空
(4)函数y=2x-1
经过
象限。
一、三、四
填空
练一练
1、下列一次函数中,y的值随x的增大而减小
的有________
(2)、(4)
2、函数
的共同性质是(
)
A
它们的图象都不经过第二象限
B
它们的图象都不经过原点
C
函数y都随自变量x的增大而增大
D
函数y都随自变量x的增大而减小
D
3.下列哪个图像是一次函数y=-3x+5
和y=2x-4的大致图像( )
(A)
(B)
(C)
(D)
B
历史使人聪明,诗歌使人机智,数学使人精细。
1、有下列函数:①y=2x+1,
②y=-3x+4,
③
y=0.5x,
④y=x-6;
①③④
②
③
①
函数y随x的增大而增大的是__________;
其中过原点的直线是________;
函数y随x的增大而减小的是___________;
图象在第一、二、三象限的是________
。
练一练
2、根据下列一次函数y=kx+b(k
≠
0)的草图回答出各图中k、b的符号:
k___0,b___0
k___0,b___0
k___0,b___0
k___0,b___0
>
<
>
>
>
<
<
<
经过一,二,三象限
经过一,三四象限
经过一,二,四象限
经过二,三,四象限
y
x
0
(D)
y
x
0
(A
)
y
x
0
(
C
)
y
x
0
(B)
小试牛刀
3、已知函数
y
=
kx的图象在二、四象限,那么函数y
=
kx-k的图象可能是(
)
B
例1
、已知函数y=(m+2)x+
(1)当m取何值时,y随x的增大而增大?
这时它的图象经过哪些象限?
(2)当
m取何值时,y随x的增大而减小?
这时它的图象经过哪些象限?
例2、
已知一次函数y=kx-k,且y随x的增大而增大,试判断它的图象经过哪几个象限?
拓展与应用
1、一次函数y=kx+b中,kb>0,且y随x的增大而
减小,则它的图象大致为(
)
2.
写出m的3个值,使相应的一次函数
y
=
(2m-1)x+2的值都是随x的增大而增大
C
3.如果一次函数y=kx-3k+6的图象经
过原点,那么k的值为_________。
4.写出m的3个值,使相应的一次函数
y
=
(2m-1)x+2的值都是随x的增大而减小.
K=2
可以写无数个,只要满足2m-1<0就可以了。
例如:m=0.m=-1,m=-2
小结:
本节课的主要内容有:
1.正比例函数的特点是什么?
2.一次函数及其图像的性质有哪些?
3.函数图像的位置关系有几种?
4.关于函数y=kx+b图像的大致
位置跟k,b的关系。
例1
在同一平面直角坐标系中画出下列每组函数的图象:
一次函数y=kx+b(k≠0)
图象的画法
(两点)
比较下列一对一次函数的图象有什么共同点,
有什么不同点?
K相同
b不同
K相同
b不同
直线(图象)平行
直线(图象)平行
对于直线y=k1x+b1与直线
y=k2x+b2
当k1=k2
,
b1≠b2
时,两直线平行
;
K不同
b相同
直线(图象)相交
当k1
≠
k2
,
b1=b2
时,两直线相交于点(0,b)
;
画出一次函数
的图象
3
1
y
3
0
X
观察分析:
当一个点在直线上从左向右移动时,它的位置怎样变化
自变量x由___到___
函数y的值从___到___
大
小
小
大
画出一次函数
的图象
3
1
y
3
0
X
观察分析:
自变量x由___到___
函数y的值从___到___
大
小
小
大
函数y=3x-2的图象是否也有这种现象
当k>0时,y随x的增大而增大,
结论
的图象
观察分析:
自变量x由___到___
函数y的值从___到___
大
小
小
大
当k<0时,y随x的增大而减小,
结论
五.想一想
1)x从0开始逐渐增
大时,y=2x+6和y=5x
哪一个的值先达到20?
这说明了什么?
-15
o
-10
10
15
5
10
15
-5
-5
-10
x
20
5
y
y=5x
y=2x+6
你看出来了吗?
(3)直线y=2x+6与y=-x+6的位置关系如何?
-6
o
-4
4
6
2
4
6
-2
-2
-4
x
y
2
y=-x+6
y=2x+6
相交
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
