第五章 平行四边形 单元测试题(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章平行四边形单元测试题
(时间:90分钟 满分:120分)
一、选择题(每小题4分,共48分)
1.平行四边形ABCD中,若∠A=120°,则∠C的度数为( )
A. 120° B. 90° C. 60° D. 45°
2.八边形的内角和等于( )
A. 1440° B. 1080° C. 720° D. 540°
3.如图所示,平行四边形ABCD中,AC的垂直平分线交AD于点E,且△CDE的周长为8,则平行四边形ABCD的周长是( )
A. 10 B. 12 C. 14 D. 16
第3题图 第4题图
4.如图,平行四边形ABCD中,对角线AC,BD相交于点O,将△AOD平移至△BEC的位置,则图中与OA相的等其他线段有( )
A. 1条 B. 2条 C. 3条 D. 4条
5.已知四边形ABCD的对角线相交于点O,则下列条件不能判断四边形ABCD为平行四边形的条件是( )
A. AD=BC, AB=CD B.∠ABC=∠ADC,∠BAD=∠BCD
C.AB∥CD,∠ABC=∠ADC D. AC=BD, OA=OB
6.一个多边形的内角和与外角和之和为2520°,则这个多边形的对角线条数为( )
A. 54 B. 108 C. 77 D. 154
7.(绵阳)如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )
6 B. 12 C. 20 D. 24
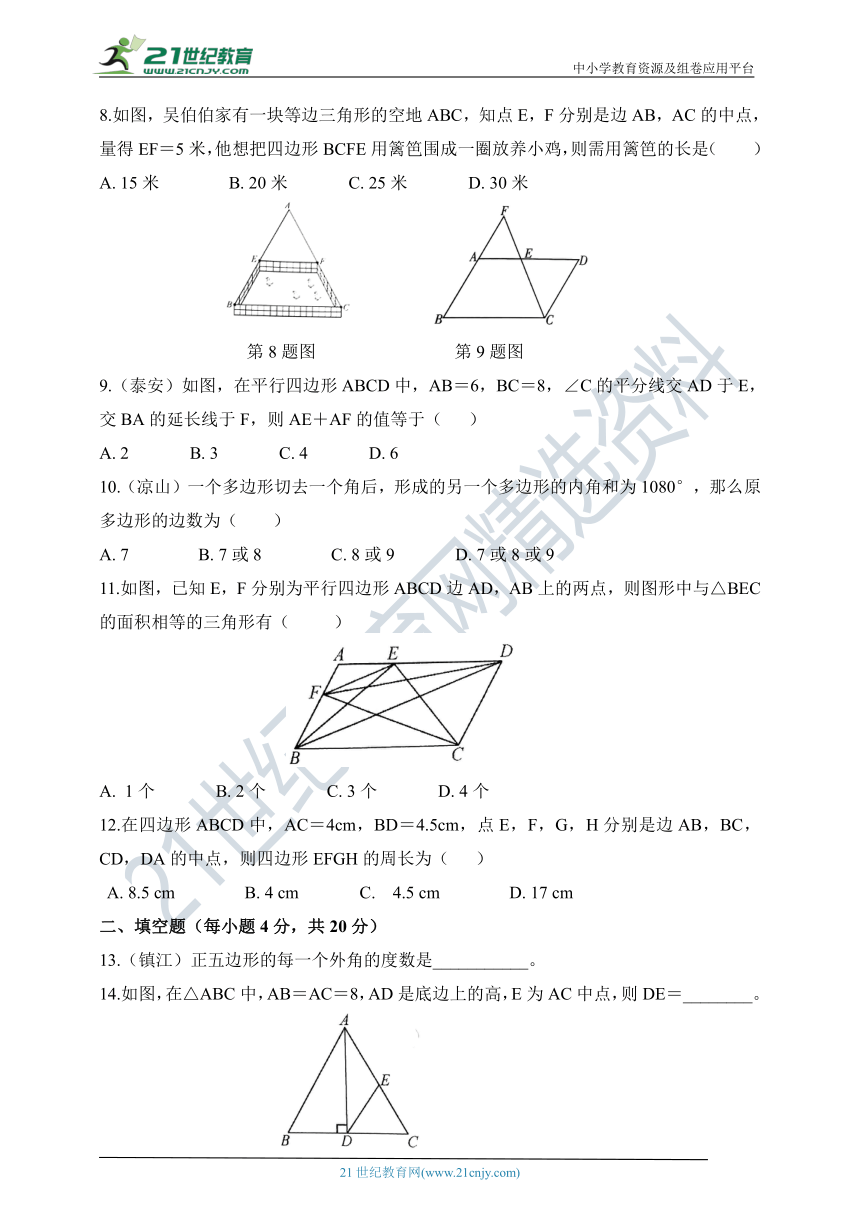
8.如图,吴伯伯家有一块等边三角形的空地ABC,知点E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需用篱笆的长是( )
A. 15米 B. 20米 C. 25米 D. 30米
第8题图 第9题图
9.(泰安)如图,在平行四边形ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A. 2 B. 3 C. 4 D. 6
10.(凉山)一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A. 7 B. 7或8 C. 8或9 D. 7或8或9
11.如图,已知E,F分别为平行四边形ABCD边AD,AB上的两点,则图形中与△BEC的面积相等的三角形有( )
1个 B. 2个 C. 3个 D. 4个
12.在四边形ABCD中,AC=4cm,BD=4.5cm,点E,F,G,H分别是边AB,BC,CD,DA的中点,则四边形EFGH的周长为( )
A. 8.5 cm B. 4 cm C. 4.5 cm D. 17 cm
二、填空题(每小题4分,共20分)
13.(镇江)正五边形的每一个外角的度数是___________。
14.如图,在△ABC中,AB=AC=8,AD是底边上的高,E为AC中点,则DE=________。
15.将一张平行四边形的纸片对折一次,使得折痕平分这个平行四边形的面积,则这条折痕必通过___________。
16.如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,点P,Q分别从A,C同时出发,P以1 cm/s的速度由A向D运动,Q以2 cm/s的速度由C出发向B运动,______秒后四边形ABQP是平行四边形.
17.在平面直角坐标系中,有A(0,1),B(-1,0)、C(1,0)三点坐标,若点D与A,B,C三点构成平行四边形,请写出所有符合条件的点D的坐标___________。
三、解答题(共52分)
18.(6分)如图,已知在四边形ABCD中,AD=BC,∠D=∠DCE.
求证:四边形ABCD是平行四边形。
19.(8分)如图,在平行四边形ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F.
(1)求证:△ABE≌△DFE。
(2)试连接BD,AF,判断四边形ABDF的形状,并证明你的结论。
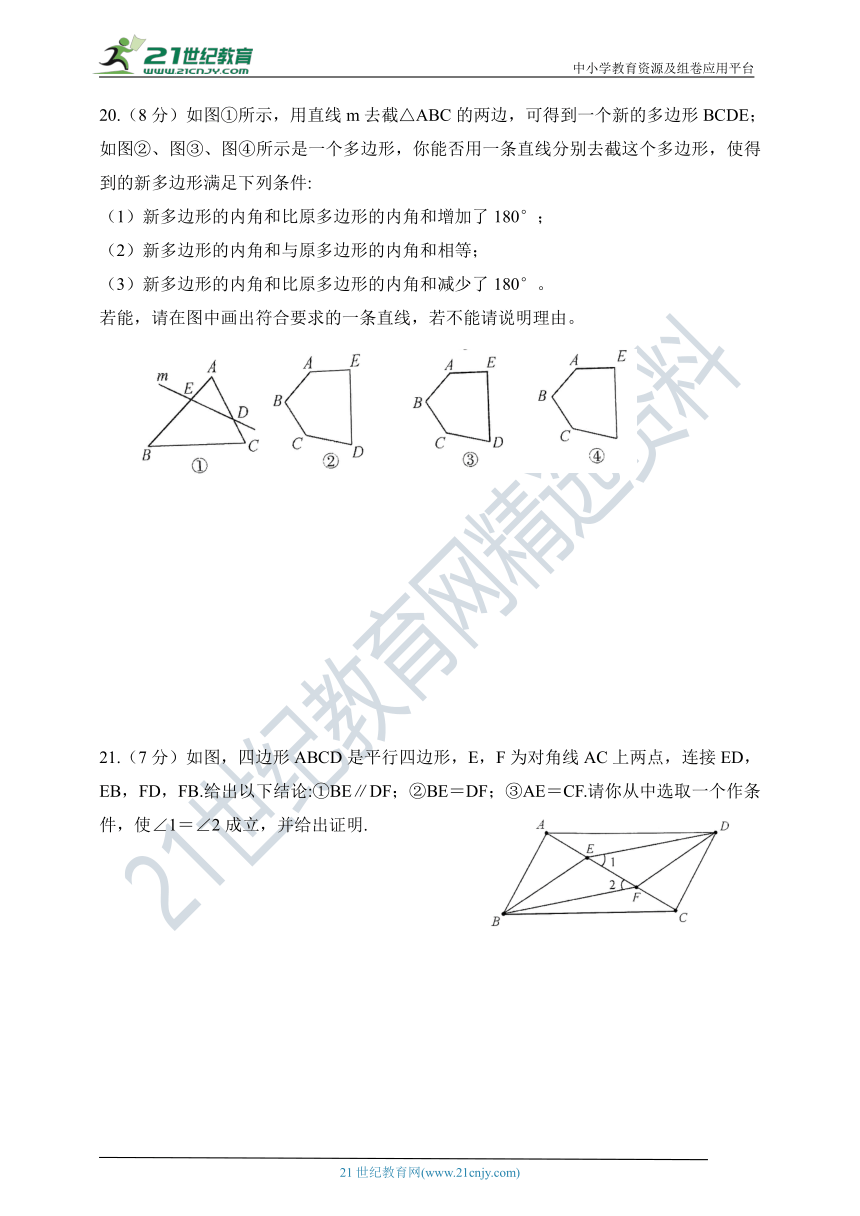
20.(8分)如图①所示,用直线m去截△ABC的两边,可得到一个新的多边形BCDE;如图②、图③、图④所示是一个多边形,你能否用一条直线分别去截这个多边形,使得到的新多边形满足下列条件:
(1)新多边形的内角和比原多边形的内角和增加了180°;
(2)新多边形的内角和与原多边形的内角和相等;
(3)新多边形的内角和比原多边形的内角和减少了180°。
若能,请在图中画出符合要求的一条直线,若不能请说明理由。
21.(7分)如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个作条件,使∠1=∠2成立,并给出证明.
22.(8分)如图,在△ABC中,AB=AC,CD是AB边上的中线,延长AB到点E,使BE=AB,连接CE.求证:CD=CE。
23.(7分)如下图所示:
根据以上信息,你能知道小华求的是几边形的内角和吗?少加的那个内角是多少度?
24.(8分)如图,四边形ABCD为平行四边形,M,N分别从D到A、从B到C运动,速度相同,E,F分别从A到B、从C到D运动,速度相同.它们之间用橡皮绳连紧.
(1)没有出发时,这两条橡皮绳有何关系?
(2)若同时出发,这两条橡皮绳还有(1)中的结论吗?为什么?
参考答案
A 2. B 3. D 4. B 5. D 6. C 7. D 8. C
C 10. D 11. C 12. A
72? 14. 4 15. 对角线的交点 16. 2
17. (-2,0)或(0,-1)或(2,1)
18.证明:∵∠D=∠DCE,∴AD∥BC.又∵AD=BC,∴四边形ABCD是平行四边形。
19.解:(1)∵四边形ABCD是平行四边形,∴AB∥CD.∴∠A=∠EDF,∠ABE=∠F.∵点E是AD的中点,∴AE=DE∴△ABE≌△DFE。
(2)四边形ABDF是平行四边形山证明:∵△ABE≌△DFE,∴BE=FE.又∵AE=DE,∴四边形ABDF是平行四边形。
20.解:都可以画出,如图所示,其中图②中的新多边形为 ABCDHG;图③中的新多边形为 ABCDF;图④中的新多边形为ABCD.
21.解:(方法1)补充条件:③AE=CF.
证明:∵AE=CF,∴AF=CE.∵四边形ABCD是平行四边形,
∴AB= CD, AB//CD.∴∠BAF=∠DCE.
∴△ABF≌△CDE. ∴∠1=∠2。
(方法2)补充条件:①BE// DF.
证明: "BE// DF,∴∠BEC=∠DFA.∴∠BEA=∠DFC.
∵四边形ABCD是平行四边形,∴AB=CD, AB//CD.∴∠BAE=∠DCF.
∴△ABE≌△CDF.∴BE=DF.∴四边形BFDE是平行四边形,∴DE// BF. ∴∠1=∠2.
22,证明:取AC的中点F,连接BF(图略).
∵AB=AC,∴∠ABC=∠ACB.又∵D为AB的中点,∴BD=CF.
∴△BCD≌△CBF(SAS).∴BF=CD. ∴BE=AB,∴BF是△AEC的中位线。
∴BF=CE. ∴ CD=CE.
23,解:由多边形的内角和公式(n-2)×180?,可知,多边形的内角和应是180的整数倍,而1125°÷180?=6.25,所以小华求的是九边形的内角和,少加的那个内角为(9-2) ×180?-1 125°= 135°。
24,解:(1)没有出发时,这两条绳子相互平分,理由如下:如图1,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,即EF与MN相互平分.
(2)若同时出发,这两条绳子还有(1)中的结论,理由如下:∵四边形ABCD是平行四边形,∴∠A=∠C.又∵M,N分别从D到A、从B到C,速度相同, E, F分别从A到B、从C到D,速度相同,∴AE=CF,AM=CN.∴在△AEM与△CFN中,
AE=CF,∠A=∠C,AM=CN,∴△AEM≌△CFN(SAS).
∴EM=FN.同理EN=MF。∴四边形ENFM为平行四边形。∴EF与MN相互平分。
_21?????????è?????(www.21cnjy.com)_
第五章平行四边形单元测试题
(时间:90分钟 满分:120分)
一、选择题(每小题4分,共48分)
1.平行四边形ABCD中,若∠A=120°,则∠C的度数为( )
A. 120° B. 90° C. 60° D. 45°
2.八边形的内角和等于( )
A. 1440° B. 1080° C. 720° D. 540°
3.如图所示,平行四边形ABCD中,AC的垂直平分线交AD于点E,且△CDE的周长为8,则平行四边形ABCD的周长是( )
A. 10 B. 12 C. 14 D. 16
第3题图 第4题图
4.如图,平行四边形ABCD中,对角线AC,BD相交于点O,将△AOD平移至△BEC的位置,则图中与OA相的等其他线段有( )
A. 1条 B. 2条 C. 3条 D. 4条
5.已知四边形ABCD的对角线相交于点O,则下列条件不能判断四边形ABCD为平行四边形的条件是( )
A. AD=BC, AB=CD B.∠ABC=∠ADC,∠BAD=∠BCD
C.AB∥CD,∠ABC=∠ADC D. AC=BD, OA=OB
6.一个多边形的内角和与外角和之和为2520°,则这个多边形的对角线条数为( )
A. 54 B. 108 C. 77 D. 154
7.(绵阳)如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )
6 B. 12 C. 20 D. 24
8.如图,吴伯伯家有一块等边三角形的空地ABC,知点E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需用篱笆的长是( )
A. 15米 B. 20米 C. 25米 D. 30米
第8题图 第9题图
9.(泰安)如图,在平行四边形ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A. 2 B. 3 C. 4 D. 6
10.(凉山)一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A. 7 B. 7或8 C. 8或9 D. 7或8或9
11.如图,已知E,F分别为平行四边形ABCD边AD,AB上的两点,则图形中与△BEC的面积相等的三角形有( )
1个 B. 2个 C. 3个 D. 4个
12.在四边形ABCD中,AC=4cm,BD=4.5cm,点E,F,G,H分别是边AB,BC,CD,DA的中点,则四边形EFGH的周长为( )
A. 8.5 cm B. 4 cm C. 4.5 cm D. 17 cm
二、填空题(每小题4分,共20分)
13.(镇江)正五边形的每一个外角的度数是___________。
14.如图,在△ABC中,AB=AC=8,AD是底边上的高,E为AC中点,则DE=________。
15.将一张平行四边形的纸片对折一次,使得折痕平分这个平行四边形的面积,则这条折痕必通过___________。
16.如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,点P,Q分别从A,C同时出发,P以1 cm/s的速度由A向D运动,Q以2 cm/s的速度由C出发向B运动,______秒后四边形ABQP是平行四边形.
17.在平面直角坐标系中,有A(0,1),B(-1,0)、C(1,0)三点坐标,若点D与A,B,C三点构成平行四边形,请写出所有符合条件的点D的坐标___________。
三、解答题(共52分)
18.(6分)如图,已知在四边形ABCD中,AD=BC,∠D=∠DCE.
求证:四边形ABCD是平行四边形。
19.(8分)如图,在平行四边形ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F.
(1)求证:△ABE≌△DFE。
(2)试连接BD,AF,判断四边形ABDF的形状,并证明你的结论。
20.(8分)如图①所示,用直线m去截△ABC的两边,可得到一个新的多边形BCDE;如图②、图③、图④所示是一个多边形,你能否用一条直线分别去截这个多边形,使得到的新多边形满足下列条件:
(1)新多边形的内角和比原多边形的内角和增加了180°;
(2)新多边形的内角和与原多边形的内角和相等;
(3)新多边形的内角和比原多边形的内角和减少了180°。
若能,请在图中画出符合要求的一条直线,若不能请说明理由。
21.(7分)如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个作条件,使∠1=∠2成立,并给出证明.
22.(8分)如图,在△ABC中,AB=AC,CD是AB边上的中线,延长AB到点E,使BE=AB,连接CE.求证:CD=CE。
23.(7分)如下图所示:
根据以上信息,你能知道小华求的是几边形的内角和吗?少加的那个内角是多少度?
24.(8分)如图,四边形ABCD为平行四边形,M,N分别从D到A、从B到C运动,速度相同,E,F分别从A到B、从C到D运动,速度相同.它们之间用橡皮绳连紧.
(1)没有出发时,这两条橡皮绳有何关系?
(2)若同时出发,这两条橡皮绳还有(1)中的结论吗?为什么?
参考答案
A 2. B 3. D 4. B 5. D 6. C 7. D 8. C
C 10. D 11. C 12. A
72? 14. 4 15. 对角线的交点 16. 2
17. (-2,0)或(0,-1)或(2,1)
18.证明:∵∠D=∠DCE,∴AD∥BC.又∵AD=BC,∴四边形ABCD是平行四边形。
19.解:(1)∵四边形ABCD是平行四边形,∴AB∥CD.∴∠A=∠EDF,∠ABE=∠F.∵点E是AD的中点,∴AE=DE∴△ABE≌△DFE。
(2)四边形ABDF是平行四边形山证明:∵△ABE≌△DFE,∴BE=FE.又∵AE=DE,∴四边形ABDF是平行四边形。
20.解:都可以画出,如图所示,其中图②中的新多边形为 ABCDHG;图③中的新多边形为 ABCDF;图④中的新多边形为ABCD.
21.解:(方法1)补充条件:③AE=CF.
证明:∵AE=CF,∴AF=CE.∵四边形ABCD是平行四边形,
∴AB= CD, AB//CD.∴∠BAF=∠DCE.
∴△ABF≌△CDE. ∴∠1=∠2。
(方法2)补充条件:①BE// DF.
证明: "BE// DF,∴∠BEC=∠DFA.∴∠BEA=∠DFC.
∵四边形ABCD是平行四边形,∴AB=CD, AB//CD.∴∠BAE=∠DCF.
∴△ABE≌△CDF.∴BE=DF.∴四边形BFDE是平行四边形,∴DE// BF. ∴∠1=∠2.
22,证明:取AC的中点F,连接BF(图略).
∵AB=AC,∴∠ABC=∠ACB.又∵D为AB的中点,∴BD=CF.
∴△BCD≌△CBF(SAS).∴BF=CD. ∴BE=AB,∴BF是△AEC的中位线。
∴BF=CE. ∴ CD=CE.
23,解:由多边形的内角和公式(n-2)×180?,可知,多边形的内角和应是180的整数倍,而1125°÷180?=6.25,所以小华求的是九边形的内角和,少加的那个内角为(9-2) ×180?-1 125°= 135°。
24,解:(1)没有出发时,这两条绳子相互平分,理由如下:如图1,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,即EF与MN相互平分.
(2)若同时出发,这两条绳子还有(1)中的结论,理由如下:∵四边形ABCD是平行四边形,∴∠A=∠C.又∵M,N分别从D到A、从B到C,速度相同, E, F分别从A到B、从C到D,速度相同,∴AE=CF,AM=CN.∴在△AEM与△CFN中,
AE=CF,∠A=∠C,AM=CN,∴△AEM≌△CFN(SAS).
∴EM=FN.同理EN=MF。∴四边形ENFM为平行四边形。∴EF与MN相互平分。
_21?????????è?????(www.21cnjy.com)_
