3.因式分解复习(新初三数学基础班)2020年(共30张PPT)
文档属性
| 名称 | 3.因式分解复习(新初三数学基础班)2020年(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 55.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 12:16:20 | ||
图片预览











文档简介
(共30张PPT)
态度决定高度
因式分解
x?-5x
x?-9
x?+8x+16
x?+5x+6
x?-3x+2
=(x+3)(x-3)平方差公式
=x(x-5)提取公因式
=(x+4)?完全平方公式
?
(x+3)(x+2)
(x-2)(x-1)
因式分解
十字
相乘
(
)×(
)
x
x
+m
+n
X?
+xm
+xn
+mn
=
=
X?
+(m+n)x
+mn
(m+n)
+mn
因式分解
x?+5x+4
5
4
1×4
2×2
X?
+(m+n)x+mn
√
x
x
1
4
=(x+1)(x+4)
x?+5x-6
+5
-6
1×6
2×3
√
x
x
-1
6
=(x+1)(x+4)
思考:
x?+bx=12中b为何值时可以用十字相乘方法因式分解?
例题
利用十字相乘法因式分解:
(1)
(2)
=(+3)(+9)
=(+3)(-8)
(3)36
=(-4)(-9)
(4)
=(-6)(+8)
例题
利用十字相乘法因式分解:
(1)
(2)
=()()
=()()
拓展:
二次项系数不为1如何使用十字相乘因式分解?
__________
概
念
性
质
运
算
分式
什么是分式?
分式
形如
的式子
(A,B是整式,且B中含有字母,B≠0)
A
B
三大条件
无意义的条件是
有意义的条件是
值为0的条件是
B=0
B≠0
A=0
B≠0
例题3
1、若分式的值为0,则的值为________
-3
值为0的条件是
A=0
B≠0
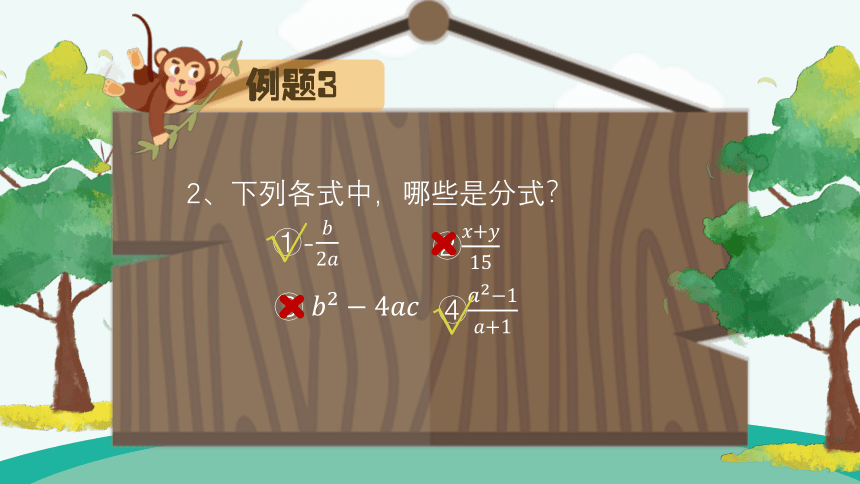
例题3
2、下列各式中,哪些是分式?
①-
②
③
④
√
√
×
×
变式训练3
1、若分式-
有意义,则的取值范围是___________
≠±4
2、若分式
意义,则________
-1
有意义的条件是
B≠0
基本性质
分式的分子和分母同乘(或除以)一个不为零的整式,分式的值不变。
=
=
其中M是不等于0的整式
分式的约分与通分
约分根据分式的基本性质将分子、分母中的_________约去,叫做分式的约分
约分的结果必须是_________或______
通分根据分式的基本性质将几个异分母的分式化为_________的分式,这种变形叫分式的通分
通分的关键是确定___________
最简公分母
例题4
已知,则代数式=
的值是(
)
A.
B.
C.
D.
D
例题5
约分=
A.
B.
C.
D.
D
加减运算
同分母
=
异分母
=
乘除运算
=
=
乘方运算
=为整数)
括
号
分
式
的
运
算
例题6
1、计算
(1)·
=
·
=
(2)÷·
=·
·
=
变式训练5
[2017.深圳]先化简,再求值
()÷,其中=-1
当=-1时
原式=
×
=
=-1
变式训练5
[2018.深圳]先化简,再求值
(1)÷,其中=2
当=2时
原式=
·
=
=
1、将下列多项式因式分解,结果中不含有因式的是(
)
A.-1
B.+
D.
C.
+
()()
()
()()
()?
C
2、下列代数式:①
②
③
④
⑤
⑥,在字母取任何值的情况下都有意义的代数式个数为(
)
C.4
B.3
D.5
A.
A
3、计算的结果是
(
)
A.
C.
D.
B.
B
4、已知,则的值为
(
)
A.
B.
D.
C.
C
5、计算
(1)
()·
原式=
=
=
(2)()÷
原式=(-)·
=
·
=
6、(2010·深圳)先化简分式÷-,然后在0,1,2,3中选一个你认为合适的值,代入求值
原式=
÷-
=
÷+
=
+
=
+
=2
若使分式有意义
则(+3)≠0,且-1
≠0
解得,≠1,≠0且≠-3
∴在0,1,2,3,中≠0且≠1即可
当=2时,原式=24
7、化简
()÷
原式=
=
=
=
8、因式分解
原式=
()
=
()
3
2
1
1、下列因式分解正确的是(
)
A.
B.
C.
D.
7、因式分解:
(1)
(2)
D
=
=
2、计算的结果是(
)
A.
B.
C.
D.2
D
3、(1)若分式的值为0,则的值为_________
(2)已知分式,当为________时的值为零
(3)若=
0,则分式-
=_________
-4
2
1
6、先化简分式,然后在-1,1,2三个数中任选一个合适的数的值,代入求值
当=2时,原式=5
课堂小结
记得订正例题
态度决定高度
因式分解
x?-5x
x?-9
x?+8x+16
x?+5x+6
x?-3x+2
=(x+3)(x-3)平方差公式
=x(x-5)提取公因式
=(x+4)?完全平方公式
?
(x+3)(x+2)
(x-2)(x-1)
因式分解
十字
相乘
(
)×(
)
x
x
+m
+n
X?
+xm
+xn
+mn
=
=
X?
+(m+n)x
+mn
(m+n)
+mn
因式分解
x?+5x+4
5
4
1×4
2×2
X?
+(m+n)x+mn
√
x
x
1
4
=(x+1)(x+4)
x?+5x-6
+5
-6
1×6
2×3
√
x
x
-1
6
=(x+1)(x+4)
思考:
x?+bx=12中b为何值时可以用十字相乘方法因式分解?
例题
利用十字相乘法因式分解:
(1)
(2)
=(+3)(+9)
=(+3)(-8)
(3)36
=(-4)(-9)
(4)
=(-6)(+8)
例题
利用十字相乘法因式分解:
(1)
(2)
=()()
=()()
拓展:
二次项系数不为1如何使用十字相乘因式分解?
__________
概
念
性
质
运
算
分式
什么是分式?
分式
形如
的式子
(A,B是整式,且B中含有字母,B≠0)
A
B
三大条件
无意义的条件是
有意义的条件是
值为0的条件是
B=0
B≠0
A=0
B≠0
例题3
1、若分式的值为0,则的值为________
-3
值为0的条件是
A=0
B≠0
例题3
2、下列各式中,哪些是分式?
①-
②
③
④
√
√
×
×
变式训练3
1、若分式-
有意义,则的取值范围是___________
≠±4
2、若分式
意义,则________
-1
有意义的条件是
B≠0
基本性质
分式的分子和分母同乘(或除以)一个不为零的整式,分式的值不变。
=
=
其中M是不等于0的整式
分式的约分与通分
约分根据分式的基本性质将分子、分母中的_________约去,叫做分式的约分
约分的结果必须是_________或______
通分根据分式的基本性质将几个异分母的分式化为_________的分式,这种变形叫分式的通分
通分的关键是确定___________
最简公分母
例题4
已知,则代数式=
的值是(
)
A.
B.
C.
D.
D
例题5
约分=
A.
B.
C.
D.
D
加减运算
同分母
=
异分母
=
乘除运算
=
=
乘方运算
=为整数)
括
号
分
式
的
运
算
例题6
1、计算
(1)·
=
·
=
(2)÷·
=·
·
=
变式训练5
[2017.深圳]先化简,再求值
()÷,其中=-1
当=-1时
原式=
×
=
=-1
变式训练5
[2018.深圳]先化简,再求值
(1)÷,其中=2
当=2时
原式=
·
=
=
1、将下列多项式因式分解,结果中不含有因式的是(
)
A.-1
B.+
D.
C.
+
()()
()
()()
()?
C
2、下列代数式:①
②
③
④
⑤
⑥,在字母取任何值的情况下都有意义的代数式个数为(
)
C.4
B.3
D.5
A.
A
3、计算的结果是
(
)
A.
C.
D.
B.
B
4、已知,则的值为
(
)
A.
B.
D.
C.
C
5、计算
(1)
()·
原式=
=
=
(2)()÷
原式=(-)·
=
·
=
6、(2010·深圳)先化简分式÷-,然后在0,1,2,3中选一个你认为合适的值,代入求值
原式=
÷-
=
÷+
=
+
=
+
=2
若使分式有意义
则(+3)≠0,且-1
≠0
解得,≠1,≠0且≠-3
∴在0,1,2,3,中≠0且≠1即可
当=2时,原式=24
7、化简
()÷
原式=
=
=
=
8、因式分解
原式=
()
=
()
3
2
1
1、下列因式分解正确的是(
)
A.
B.
C.
D.
7、因式分解:
(1)
(2)
D
=
=
2、计算的结果是(
)
A.
B.
C.
D.2
D
3、(1)若分式的值为0,则的值为_________
(2)已知分式,当为________时的值为零
(3)若=
0,则分式-
=_________
-4
2
1
6、先化简分式,然后在-1,1,2三个数中任选一个合适的数的值,代入求值
当=2时,原式=5
课堂小结
记得订正例题
