人教版数学七年级上册3.1.1 一元一次方程课件(21张)
文档属性
| 名称 | 人教版数学七年级上册3.1.1 一元一次方程课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 526.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 10:39:26 | ||
图片预览






文档简介
(共22张PPT)
3.1
从算式到方程
第三章
一元一次方程
3.1.1
一元一次方程
学习目标
1.通过算术与方程方法的使用与比较,体验用方程解
决某些问题的优越性,提高解决实际问题的能力.
2.掌握方程、一元一次方程的定义以及解的概念,学
会判断某个数值是不是一元一次方程的解.(重点)
3.初步学会如何寻找问题中的等量关系,并列出方程.
(难点)
方程:
含有未知数的等式叫方程.
2.判断下列各式哪些是方程?
①1+2=3
(
)
②1+2x=4
(
)
③x+y=2
(
)
④x+1
(
)
⑤x2-1=0
(
)
⑥6a+8=3
(
)
⑦
(
)
⑧5x+2≥0
(
)
√
×
√
×
√
√
√
×
回顾思考
1.你知道什么叫做方程吗?
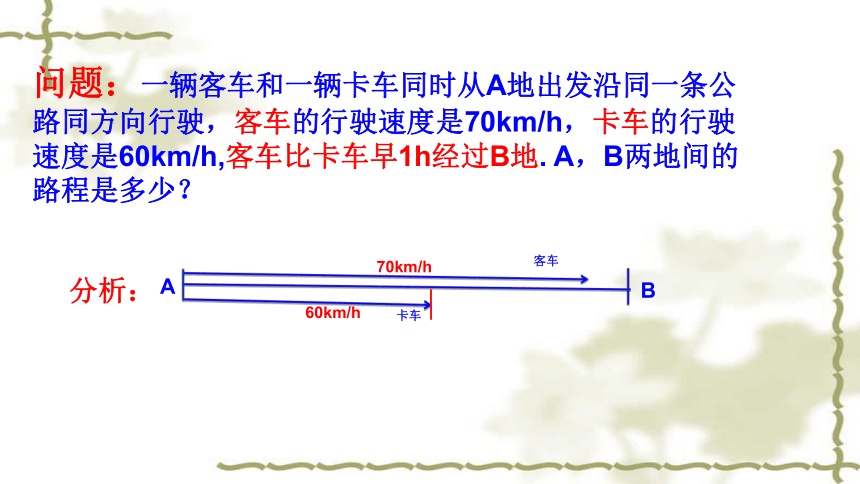
问题:一辆客车和一辆卡车同时从A地出发沿同一条公路同方向行驶,客车的行驶速度是70km/h,卡车的行驶速度是60km/h,客车比卡车早1h经过B地.
A,B两地间的路程是多少?
分析:
客车
卡车
A
B
70km/h
60km/h
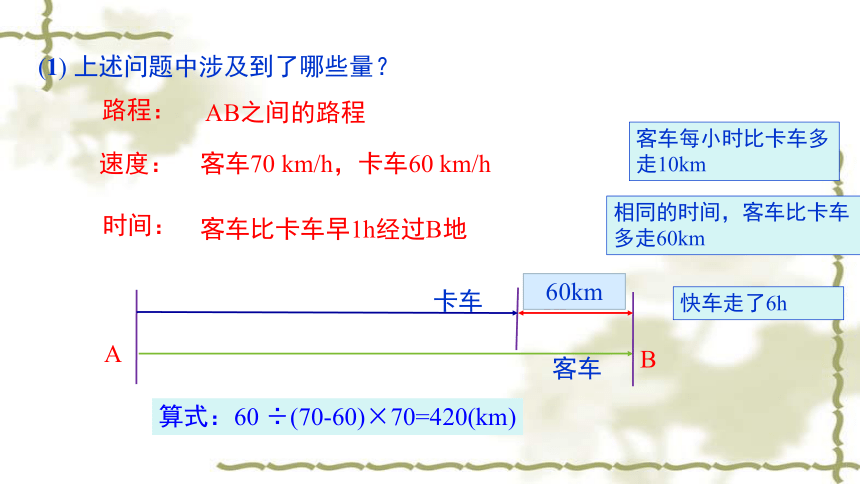
(1)
上述问题中涉及到了哪些量?
客车70
km/h,卡车60
km/h
客车比卡车早1h经过B地
AB之间的路程
速度:
时间:
路程:
A
B
客车
卡车
1h
客车每小时比卡车多走10km
60km
相同的时间,客车比卡车多走60km
快车走了6h
算式:60
÷(70-60)×70=420(km)
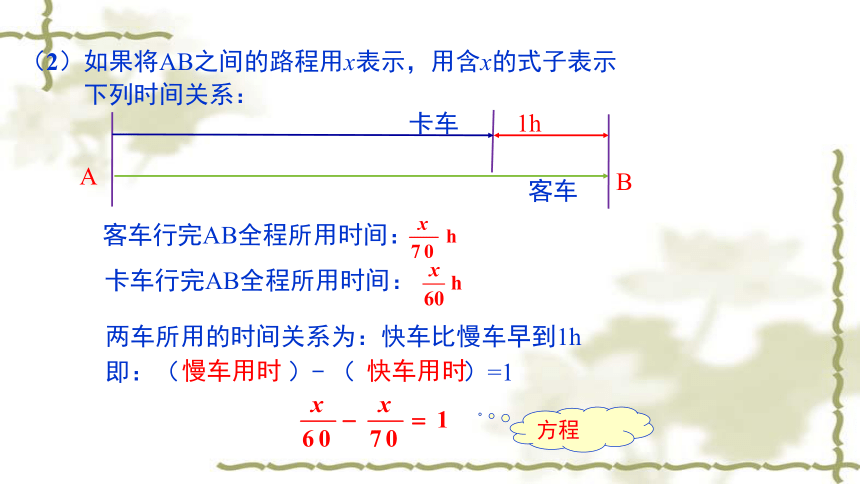
(2)如果将AB之间的路程用x表示,用含x的式子表示
下列时间关系:
客车行完AB全程所用时间:
卡车行完AB全程所用时间:
两车所用的时间关系为:快车比慢车早到1h
即:(
)-
(
)=1
慢车用时
快车用时
方程
A
B
客车
卡车
1h
比较:列算式和列方程
从算式到方程是数学的进步!
列算式:列出的算式表示解题的计算过程,
只能用已知数.对于较复杂的问题,列算式比较困难.
列方程:方程是根据题中的等量关系列出的等式.
既可用已知数,又可用未知数,解决问题比较方便.
(1)用一根长24cm的铁丝围成一个正方形,正方形的边长是多少cm?
例1
根据下列问题,设未知数并列出方程
(2)一台计算机已使用1700小时,预计每月再使用150小时,经过多
少月这台计算机的使用时间达到规定的检修时间2450小时?
(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?
列方程:
4x=24.
解:(1)如设正方形的边长为
x
cm,
解:设x月后这台计算机的使用时间达到
2450
小时,那么在
x
月里这台计算机使用了
_______小时。
列出方程:
1700+150x
=
2450
150x
解:
设这个学校的学生人数为x人,那么女生的人数
人,男生的人数
人,
列出方程:0.52x-
(1-0.52)x=80
0.52x
(1-0.52)x
女生人数
-
男生人数=80人
你能解释方程中等号两边的依据吗?
已用的时间+还可用时间150x小时=规定的检测时间2450小时.
这样的方程叫做一元一次方程.
等号两边都是整式,
(一次)
只含有一个未知数,
(一元)
未知数的次数都是1,
观察上面个方程有什么共同点?
(未知数,未知数的次数,等号的两边)
4x=24,1700+150x=2450,0.52x-(1-0.52)x=80
分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法.
请同学们思考:
1.
怎样将一个实际问题转化为方程问题?
2.列方程的依据是什么?
设未知数列方程
一元一次方程
抓关键句子找等量关系
实际问题
列方程的步骤:
①审题:分析题中的已知量,未知量,明确各个量之间的关系;
②设未知数:用字母(如x)表示题目中的未知数;
③找相等关系:找出实际问题中的相等关系
④列方程:根据相等关系列出方程。
归纳总结
下列哪些是一元一次方程?
(1)2x+1
;
(2)3y+24=33
;
(3)3x-8=5x+4
;(4)
3x?-4+x=0
;
(5)-3x+9=18y;
(6)4b+7>13
;
(7)
.
(8)2π+6=9
√
√
练一练
(1)环形跑道一周长400m,沿跑道跑多少周,可以跑3000m?
(2)甲种铅笔每枝0.3元,乙种铅笔每枝0.6元,用9元钱买了
两种铅笔共20枝,两种铅笔各买了多少枝?
(3)一个梯形的下底比上底多2㎝,高是5㎝,面积是40㎝2,
求上底。
解:(1)
设跑x周.
列方程
400x=3000
(2)设甲种铅笔买了x枝,乙种铅笔买了(20-x)枝.
列方程
0.3x+0.6(20-x)=9
(3)设上底为x
cm,下底为(x+2)cm.
列方程
根据下列问题,设未知数,列出方程。
对于方程4x=24,容易知道
x
=
6可以使等式成立,
对于方程
170+15x
=245,你知道
x
等于什么时,等式成立吗?我们来试一试.
x
1
2
3
4
5
6
…
…
我们知道当x=5时,170+15x的值是245,所以方程
170+15x
=
245中的未知数的值应是5.
185
200
215
230
245
260
170+15x
x=420是
方程的解吗?
方程的解:使方程中等号左右两边相等的未知数的值叫方程的解。
解方程:就是求出使方程中等号左右两边相等的未知数的值的过程。
思考:
x=1000和x=2000中哪一个是方程
0.52x-(1-0.52)x=80的解?
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,
右边=80,左边≠右边,所以x=1000不是此方程的解.
当x=2000时,
方程左边=
0.52×2000-(1-0.52)×2000=1040-960=80,
右边=80,左边=右边,所以x=2000是此方程的解.
1.
将数值代入方程左边进行计算,
2.
将数值代入方程右边进行计算,
3.
若左边=右边,则是方程的解,反之,则不是.
判断一个数值是不是方程的解的步骤:
练一练
检验
x
=
3是不是方程
2x-3
=
5x-15的解.
解:把
x
=3分别代入方程的左边和右边,得
当x
=
4,5,6时呢?
左边=2×3-3=3,
右边=5×3-15=0.
∵左边≠右边,
∴
x
=3不是方程的解.
1.若k是方程
2x=3
的解,则
4k+2=______.
2.若
是关于x的一元一次方程,则
n=______.
3.已知方程
是关于x的一元一次方程,则
a=______.
1.
一元一次方程的概念:
只含有一个未知数,未知数的次数是1,等号两
边都是整式,这样的方程叫做一元一次方程.
2.
方程的解:
解方程就是求出使方程中等号两边相等的未知
数的值,这个值就是方程的解.
3.1
从算式到方程
第三章
一元一次方程
3.1.1
一元一次方程
学习目标
1.通过算术与方程方法的使用与比较,体验用方程解
决某些问题的优越性,提高解决实际问题的能力.
2.掌握方程、一元一次方程的定义以及解的概念,学
会判断某个数值是不是一元一次方程的解.(重点)
3.初步学会如何寻找问题中的等量关系,并列出方程.
(难点)
方程:
含有未知数的等式叫方程.
2.判断下列各式哪些是方程?
①1+2=3
(
)
②1+2x=4
(
)
③x+y=2
(
)
④x+1
(
)
⑤x2-1=0
(
)
⑥6a+8=3
(
)
⑦
(
)
⑧5x+2≥0
(
)
√
×
√
×
√
√
√
×
回顾思考
1.你知道什么叫做方程吗?
问题:一辆客车和一辆卡车同时从A地出发沿同一条公路同方向行驶,客车的行驶速度是70km/h,卡车的行驶速度是60km/h,客车比卡车早1h经过B地.
A,B两地间的路程是多少?
分析:
客车
卡车
A
B
70km/h
60km/h
(1)
上述问题中涉及到了哪些量?
客车70
km/h,卡车60
km/h
客车比卡车早1h经过B地
AB之间的路程
速度:
时间:
路程:
A
B
客车
卡车
1h
客车每小时比卡车多走10km
60km
相同的时间,客车比卡车多走60km
快车走了6h
算式:60
÷(70-60)×70=420(km)
(2)如果将AB之间的路程用x表示,用含x的式子表示
下列时间关系:
客车行完AB全程所用时间:
卡车行完AB全程所用时间:
两车所用的时间关系为:快车比慢车早到1h
即:(
)-
(
)=1
慢车用时
快车用时
方程
A
B
客车
卡车
1h
比较:列算式和列方程
从算式到方程是数学的进步!
列算式:列出的算式表示解题的计算过程,
只能用已知数.对于较复杂的问题,列算式比较困难.
列方程:方程是根据题中的等量关系列出的等式.
既可用已知数,又可用未知数,解决问题比较方便.
(1)用一根长24cm的铁丝围成一个正方形,正方形的边长是多少cm?
例1
根据下列问题,设未知数并列出方程
(2)一台计算机已使用1700小时,预计每月再使用150小时,经过多
少月这台计算机的使用时间达到规定的检修时间2450小时?
(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?
列方程:
4x=24.
解:(1)如设正方形的边长为
x
cm,
解:设x月后这台计算机的使用时间达到
2450
小时,那么在
x
月里这台计算机使用了
_______小时。
列出方程:
1700+150x
=
2450
150x
解:
设这个学校的学生人数为x人,那么女生的人数
人,男生的人数
人,
列出方程:0.52x-
(1-0.52)x=80
0.52x
(1-0.52)x
女生人数
-
男生人数=80人
你能解释方程中等号两边的依据吗?
已用的时间+还可用时间150x小时=规定的检测时间2450小时.
这样的方程叫做一元一次方程.
等号两边都是整式,
(一次)
只含有一个未知数,
(一元)
未知数的次数都是1,
观察上面个方程有什么共同点?
(未知数,未知数的次数,等号的两边)
4x=24,1700+150x=2450,0.52x-(1-0.52)x=80
分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法.
请同学们思考:
1.
怎样将一个实际问题转化为方程问题?
2.列方程的依据是什么?
设未知数列方程
一元一次方程
抓关键句子找等量关系
实际问题
列方程的步骤:
①审题:分析题中的已知量,未知量,明确各个量之间的关系;
②设未知数:用字母(如x)表示题目中的未知数;
③找相等关系:找出实际问题中的相等关系
④列方程:根据相等关系列出方程。
归纳总结
下列哪些是一元一次方程?
(1)2x+1
;
(2)3y+24=33
;
(3)3x-8=5x+4
;(4)
3x?-4+x=0
;
(5)-3x+9=18y;
(6)4b+7>13
;
(7)
.
(8)2π+6=9
√
√
练一练
(1)环形跑道一周长400m,沿跑道跑多少周,可以跑3000m?
(2)甲种铅笔每枝0.3元,乙种铅笔每枝0.6元,用9元钱买了
两种铅笔共20枝,两种铅笔各买了多少枝?
(3)一个梯形的下底比上底多2㎝,高是5㎝,面积是40㎝2,
求上底。
解:(1)
设跑x周.
列方程
400x=3000
(2)设甲种铅笔买了x枝,乙种铅笔买了(20-x)枝.
列方程
0.3x+0.6(20-x)=9
(3)设上底为x
cm,下底为(x+2)cm.
列方程
根据下列问题,设未知数,列出方程。
对于方程4x=24,容易知道
x
=
6可以使等式成立,
对于方程
170+15x
=245,你知道
x
等于什么时,等式成立吗?我们来试一试.
x
1
2
3
4
5
6
…
…
我们知道当x=5时,170+15x的值是245,所以方程
170+15x
=
245中的未知数的值应是5.
185
200
215
230
245
260
170+15x
x=420是
方程的解吗?
方程的解:使方程中等号左右两边相等的未知数的值叫方程的解。
解方程:就是求出使方程中等号左右两边相等的未知数的值的过程。
思考:
x=1000和x=2000中哪一个是方程
0.52x-(1-0.52)x=80的解?
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,
右边=80,左边≠右边,所以x=1000不是此方程的解.
当x=2000时,
方程左边=
0.52×2000-(1-0.52)×2000=1040-960=80,
右边=80,左边=右边,所以x=2000是此方程的解.
1.
将数值代入方程左边进行计算,
2.
将数值代入方程右边进行计算,
3.
若左边=右边,则是方程的解,反之,则不是.
判断一个数值是不是方程的解的步骤:
练一练
检验
x
=
3是不是方程
2x-3
=
5x-15的解.
解:把
x
=3分别代入方程的左边和右边,得
当x
=
4,5,6时呢?
左边=2×3-3=3,
右边=5×3-15=0.
∵左边≠右边,
∴
x
=3不是方程的解.
1.若k是方程
2x=3
的解,则
4k+2=______.
2.若
是关于x的一元一次方程,则
n=______.
3.已知方程
是关于x的一元一次方程,则
a=______.
1.
一元一次方程的概念:
只含有一个未知数,未知数的次数是1,等号两
边都是整式,这样的方程叫做一元一次方程.
2.
方程的解:
解方程就是求出使方程中等号两边相等的未知
数的值,这个值就是方程的解.
