人教版数学七年级上册4.3.3 余角和补角课件(27张)
文档属性
| 名称 | 人教版数学七年级上册4.3.3 余角和补角课件(27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 624.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 00:00:00 | ||
图片预览



文档简介
(共28张PPT)
4.3.3
余角和补角以及方位角
第四章
图形初步认识
4.3
角
学习目标
了解余角、补角的概念,掌握余角和补角的性质,并能利用余角、
补角的知识解决相关问题.(重点、难点)
2.
了解方位角的概念,并能用方位角知识解决一些简单的实际问题.(难点)
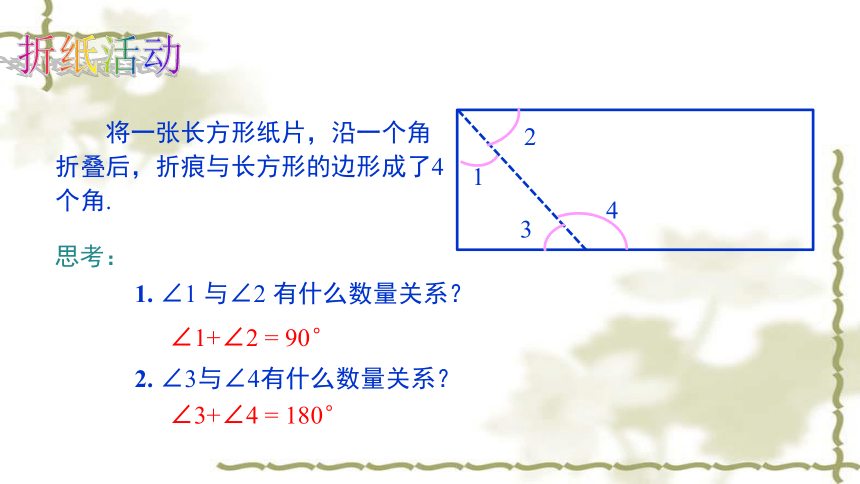
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
1
2
3
4
思考:
1.
∠1
与∠2
有什么数量关系?
∠1+∠2
=
90°
2.
∠3与∠4有什么数量关系?
∠3+∠4
=
180°
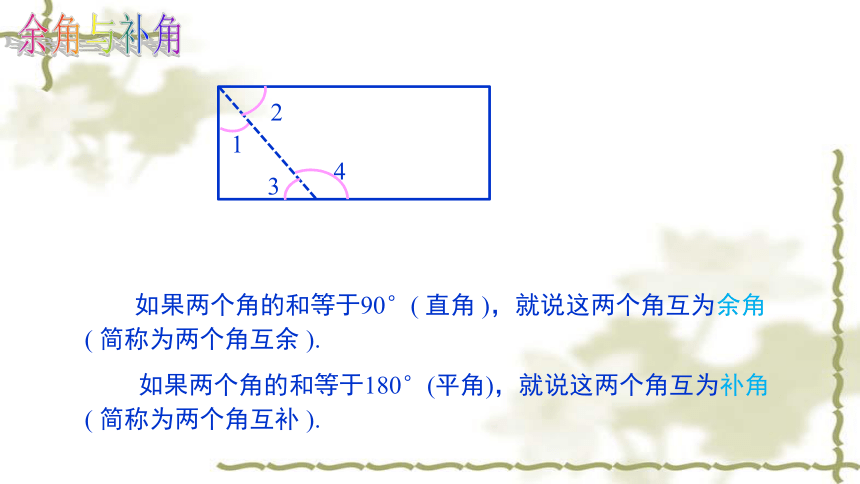
如果两个角的和等于90°(
直角
),就说这两个角互为余角
(
简称为两个角互余
).
1
2
3
4
如果两个角的和等于180°(平角),就说这两个角互为补角
(
简称为两个角互补
).
提问答疑,理解定义
如果
∠1
与∠2互余,那么∠1
的余角是∠2,同样∠2的余角是∠1
;如果∠1
与∠2互补,那么∠1
的补角是∠2,
同样∠2的补角是∠1
。
两角互余或互补,只与角的度数有关,与位置无关。
(1)定义中的“互为”一词如何理解?
(2)互余、互补的两角是否一定有公共顶点或公共边?
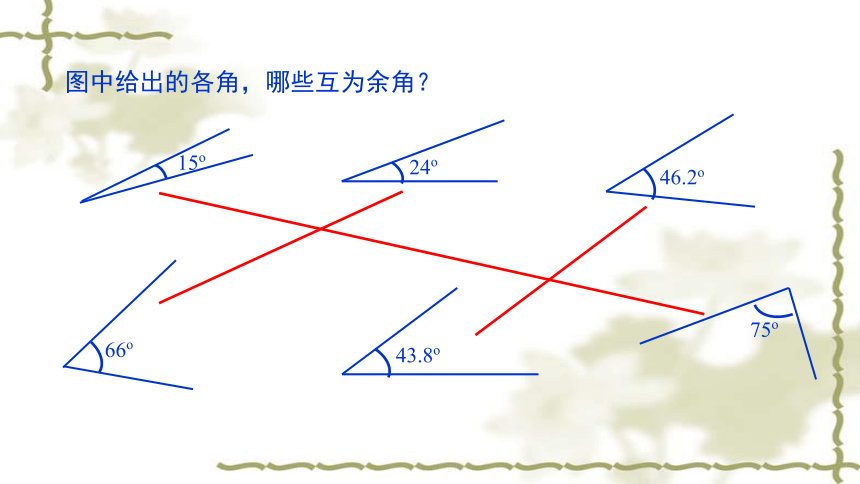
图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
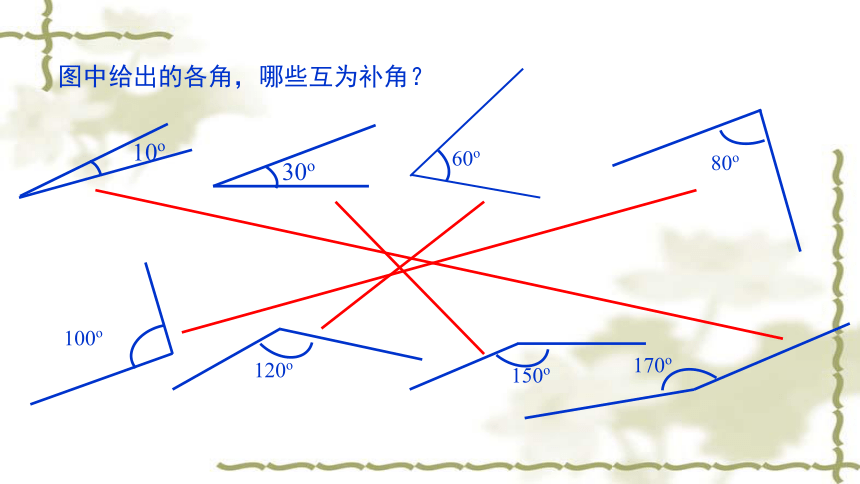
图中给出的各角,哪些互为补角?
10o
30o
80o
100o
120o
150o
170o
60o
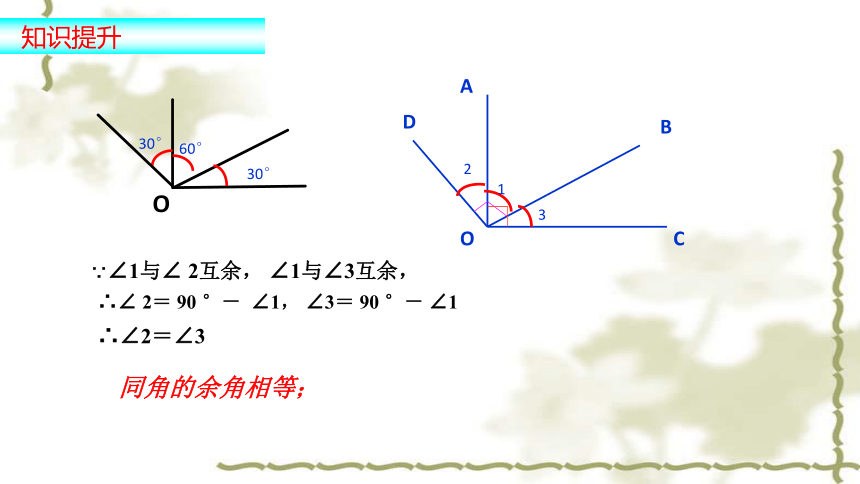
同角的余角相等;
∵∠1与∠
2互余,
∠1与∠3互余,
知识提升
O
60°
30°
B
O
C
A
D
2
1
3
∴∠
2=
90
°-
∠1,
∠3=
90
°-
∠1
∴∠2=∠3
30°
1
2
4
3
等角的余角相等。
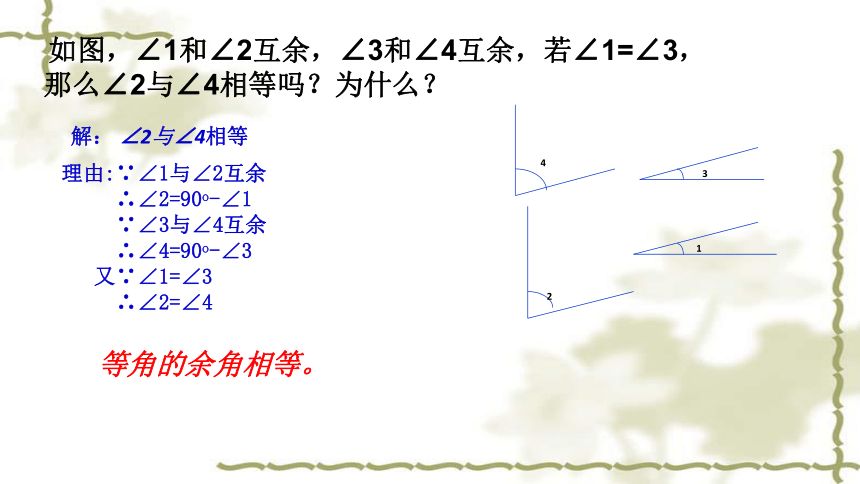
理由:∵∠1与∠2互余
∴∠2=90o-∠1
∵∠3与∠4互余
∴∠4=90o-∠3
又∵∠1=∠3
∴∠2=∠4
解:
∠2与∠4相等
如图,∠1和∠2互余,∠3和∠4互余,若∠1=∠3,
那么∠2与∠4相等吗?为什么?
如图,画出∠1的补角
1
同角的补角相等;
理由:∵∠1与∠
2互补,
∠1与∠3互补,
解:
∠2与∠3相等.
思考
1
2
3
∴∠
2=
180
°
-
∠1,
∠3=
180
°
-
∠1
∴∠2=∠3
如图,∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
3
4
解:∠2与∠4相等。
这里,我们用到了“等量减等量,差相等”。
因为∠1与∠2互补;∠3与∠4互补,
所以∠2=180°-∠1;∠4=180°-∠3,
又因为∠1=∠3,
所以∠2=∠4。
等角的补角相等
例3
如图,点A,O,B在同一直线上,射线
OD
和射线
OE
分别平分∠AOC
和∠BOC,图中哪些角互为余角?
解:因为点A,O,B在同一直线
上,所以
∠AOC
和
∠BOC
互为补角.
O
A
B
C
D
E
又因为射线
OD
和射线
OE
分别平分∠AOC
和∠BOC,
所以∠COD+∠COE=
∠AOC+
∠BOC
=
(∠AOC+∠BOC
)
=
90°.
O
A
B
C
D
E
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)∠AOD的余角是_______________,∠COD的余角是_________________;
(2
)OE是∠BOC的平分线吗?请说明理由.
变式训练
∠COE、∠BOE
O
A
B
C
D
E
∠COE、∠BOE
解:OE平分∠BOC,理由如下:∵∠DOE=90°,∴∠AOD+∠BOE=90°,
∴∠COD+∠DOE=90°,
∴∠AOD+∠BOE=∠COD+∠DOE,
∵OD平分∠AOC∴∠AOD=∠COD,
∴∠COE=∠BOE,∴OE平分∠BOC.
你知道表示方向的一个成语吗?
“四面”—东、南、西、北
“八方”--东、南、西、北和东北、东南、西北、西南
东
西
北
南
O
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
射线
OA
A
B
C
D
45°
E
G
F
H
45°
八大方位
45°
45°
射线
OB
射线
OC
射线
OD
射线
OE
射线
OF
射线
OH
射线
OG
表示方位的角(方位角)在航行、测绘等工作中经常用到。一般以正北、正南方向为基准,描述物体运动的方向。如“北偏东30°”、“南偏西25°”。
方位角的一边是表示正北或正南的射线,另一边是表示偏西或偏东的射线。
45°
如图,说出下列方位
(1)
射线
OA
表示的方向
为
.
(2)
射线
OB
表示的方向
为
___
_
.
(3)
射线
OC
表示的方向
为
.
(4)
射线
OD
表示的方向
为
.
北
东
西
南
C
A
B
D
北偏东
40°
北偏西
65°
南偏西
45°(西南)
南偏东
20°
40°
65°
70°
O
20°
例4
如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上.
同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)
方向上又分别发现了客
轮B,货轮C和海岛D.
仿照表示灯塔方位的
方法画出表示客轮B,
货轮C和海岛D方向的
射线.
东
南
西
北
60°
●
B
40°
10°
45°
C
●
●
A
●
D
O
●
1.一个角是70°39′,求它的余角和补角。
练习
2、∠A的补角是它的3倍,∠A是多少度?
B
A
O
C
3、
如图两堵墙围一个角∠AOB,但人不能进入围墙,我们如何去测这个角的大小呢?
4、如图,已知∠ACB=∠CDB=90°.
(1)
图中有哪几对互余的角?
(2)
图中哪几对角是相等的角(直角除外)?为什么?
答案:∠A+∠B=90°
∠A+∠2=90°
∠1+∠B=90°
∠1+∠2=90°
答案:∠B=∠2
∠A=∠1
(
同角的余角相等
)
(
同角的余角相等
)
A
C
D
1
2
B
5、一条船在灯塔的北偏东30°方向,那么灯塔在船的什么方向
(
)
A.南偏西30°
B.西偏南40°
C.南偏西60°
D.北偏东30°
A
分析:相对方位,度数不变,方向相反
同角或等角的
补角相等
同角或等角的
余角相等
互余
互补
两角间的数量关系
对应图形
性质
方位角
物体运动的方向与正北、正南方向之间的夹角称为方位角,一般以正北、正南为基准,用向东或向西旋转的角度表示方向
定义
书写
通常要先写北或南,再写偏东或偏西
4.3.3
余角和补角以及方位角
第四章
图形初步认识
4.3
角
学习目标
了解余角、补角的概念,掌握余角和补角的性质,并能利用余角、
补角的知识解决相关问题.(重点、难点)
2.
了解方位角的概念,并能用方位角知识解决一些简单的实际问题.(难点)
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
1
2
3
4
思考:
1.
∠1
与∠2
有什么数量关系?
∠1+∠2
=
90°
2.
∠3与∠4有什么数量关系?
∠3+∠4
=
180°
如果两个角的和等于90°(
直角
),就说这两个角互为余角
(
简称为两个角互余
).
1
2
3
4
如果两个角的和等于180°(平角),就说这两个角互为补角
(
简称为两个角互补
).
提问答疑,理解定义
如果
∠1
与∠2互余,那么∠1
的余角是∠2,同样∠2的余角是∠1
;如果∠1
与∠2互补,那么∠1
的补角是∠2,
同样∠2的补角是∠1
。
两角互余或互补,只与角的度数有关,与位置无关。
(1)定义中的“互为”一词如何理解?
(2)互余、互补的两角是否一定有公共顶点或公共边?
图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
图中给出的各角,哪些互为补角?
10o
30o
80o
100o
120o
150o
170o
60o
同角的余角相等;
∵∠1与∠
2互余,
∠1与∠3互余,
知识提升
O
60°
30°
B
O
C
A
D
2
1
3
∴∠
2=
90
°-
∠1,
∠3=
90
°-
∠1
∴∠2=∠3
30°
1
2
4
3
等角的余角相等。
理由:∵∠1与∠2互余
∴∠2=90o-∠1
∵∠3与∠4互余
∴∠4=90o-∠3
又∵∠1=∠3
∴∠2=∠4
解:
∠2与∠4相等
如图,∠1和∠2互余,∠3和∠4互余,若∠1=∠3,
那么∠2与∠4相等吗?为什么?
如图,画出∠1的补角
1
同角的补角相等;
理由:∵∠1与∠
2互补,
∠1与∠3互补,
解:
∠2与∠3相等.
思考
1
2
3
∴∠
2=
180
°
-
∠1,
∠3=
180
°
-
∠1
∴∠2=∠3
如图,∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
3
4
解:∠2与∠4相等。
这里,我们用到了“等量减等量,差相等”。
因为∠1与∠2互补;∠3与∠4互补,
所以∠2=180°-∠1;∠4=180°-∠3,
又因为∠1=∠3,
所以∠2=∠4。
等角的补角相等
例3
如图,点A,O,B在同一直线上,射线
OD
和射线
OE
分别平分∠AOC
和∠BOC,图中哪些角互为余角?
解:因为点A,O,B在同一直线
上,所以
∠AOC
和
∠BOC
互为补角.
O
A
B
C
D
E
又因为射线
OD
和射线
OE
分别平分∠AOC
和∠BOC,
所以∠COD+∠COE=
∠AOC+
∠BOC
=
(∠AOC+∠BOC
)
=
90°.
O
A
B
C
D
E
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)∠AOD的余角是_______________,∠COD的余角是_________________;
(2
)OE是∠BOC的平分线吗?请说明理由.
变式训练
∠COE、∠BOE
O
A
B
C
D
E
∠COE、∠BOE
解:OE平分∠BOC,理由如下:∵∠DOE=90°,∴∠AOD+∠BOE=90°,
∴∠COD+∠DOE=90°,
∴∠AOD+∠BOE=∠COD+∠DOE,
∵OD平分∠AOC∴∠AOD=∠COD,
∴∠COE=∠BOE,∴OE平分∠BOC.
你知道表示方向的一个成语吗?
“四面”—东、南、西、北
“八方”--东、南、西、北和东北、东南、西北、西南
东
西
北
南
O
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
射线
OA
A
B
C
D
45°
E
G
F
H
45°
八大方位
45°
45°
射线
OB
射线
OC
射线
OD
射线
OE
射线
OF
射线
OH
射线
OG
表示方位的角(方位角)在航行、测绘等工作中经常用到。一般以正北、正南方向为基准,描述物体运动的方向。如“北偏东30°”、“南偏西25°”。
方位角的一边是表示正北或正南的射线,另一边是表示偏西或偏东的射线。
45°
如图,说出下列方位
(1)
射线
OA
表示的方向
为
.
(2)
射线
OB
表示的方向
为
___
_
.
(3)
射线
OC
表示的方向
为
.
(4)
射线
OD
表示的方向
为
.
北
东
西
南
C
A
B
D
北偏东
40°
北偏西
65°
南偏西
45°(西南)
南偏东
20°
40°
65°
70°
O
20°
例4
如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上.
同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)
方向上又分别发现了客
轮B,货轮C和海岛D.
仿照表示灯塔方位的
方法画出表示客轮B,
货轮C和海岛D方向的
射线.
东
南
西
北
60°
●
B
40°
10°
45°
C
●
●
A
●
D
O
●
1.一个角是70°39′,求它的余角和补角。
练习
2、∠A的补角是它的3倍,∠A是多少度?
B
A
O
C
3、
如图两堵墙围一个角∠AOB,但人不能进入围墙,我们如何去测这个角的大小呢?
4、如图,已知∠ACB=∠CDB=90°.
(1)
图中有哪几对互余的角?
(2)
图中哪几对角是相等的角(直角除外)?为什么?
答案:∠A+∠B=90°
∠A+∠2=90°
∠1+∠B=90°
∠1+∠2=90°
答案:∠B=∠2
∠A=∠1
(
同角的余角相等
)
(
同角的余角相等
)
A
C
D
1
2
B
5、一条船在灯塔的北偏东30°方向,那么灯塔在船的什么方向
(
)
A.南偏西30°
B.西偏南40°
C.南偏西60°
D.北偏东30°
A
分析:相对方位,度数不变,方向相反
同角或等角的
补角相等
同角或等角的
余角相等
互余
互补
两角间的数量关系
对应图形
性质
方位角
物体运动的方向与正北、正南方向之间的夹角称为方位角,一般以正北、正南为基准,用向东或向西旋转的角度表示方向
定义
书写
通常要先写北或南,再写偏东或偏西
