2020-2021学年北师大版七年级数学上册第五章一元一次方程单元检测(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学上册第五章一元一次方程单元检测(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 298.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 15:16:41 | ||
图片预览




文档简介
第五章一元一次方程单元检测
一、选择题(51分)
(2017·期末·天津天津市河北区)方程
的解是
,则
的值是
A.
B.
C.
D.
(2019·期末·广东深圳市福田区)下列方程:①
;②
;③
;④
;⑤
,其中是一元一次方程的有
A.
个
B.
个
C.
个
D.以上答案都不对
(2020·同步练习)参加保险公司的医疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表:某人住院治疗后得到保险公司报销金额是
元,那么此人住院的医疗费是
A.
元
B.
元
C.
元
D.
元
(2019·期末·江苏苏州市张家港市)小淇在某月的日历中圈出相邻的三个数,算出它们的和是
,那么这三个数的位置可能是
A.
B.
C.
D.
(2019·期中·广东深圳市南山区)如图,在四边形
中,动点
从点
开始沿
的路径匀速前进到
为止.在这个过程中,
的面积
随时间
的变化关系用图象表示正确的是
A.
B.
C.
D.
(2019·单元测试·北京北京市朝阳区)下列说法错误的是
A.若
,则
B.若
,则
C.若
,则
D.若
,则
(2018·期中·北京北京市西城区)如果
是方程
的解,那么
的值是
A.
B.
C.
D.
(2020·专项·上海上海市闵行区)有下列四个等式:
①
;
②
;
③
;
④
.
其中一元一次方程有
A.
个
B.
个
C.
个
D.
个
(2020·同步练习)某道路一侧原有路灯
盏,相邻两盏灯的距离为
,,现计划全部更换为新型的节能灯,且相邻两盏灯的距离变为
,则需更换的新型节能灯有
A.
盏
B.
盏
C.
盏
D.
盏
(2018·期末)将正整数
至
按一定规律排列如图所示,从表中任取一个
的方框,方框中九个数的和可能是
A.
B.
C.
D.
(2019·期末·江苏徐州市铜山区)某个体商贩在一次买卖中,同时卖出两件上衣,售价都是
元,若按成本计,其中一件盈利
,另一件亏本
,在这次买卖中他
A.不赚不赔
B.赚
元
C.赔
元
D.赚
元
(2019·期中·广东广州市天河区)甲,乙,丙三家超市为了促销一种定价均为
元的商品,甲超市连续两次降价
,乙超市一次性降价
,丙超市第一次降价
,第二次降价
,此时顾客要购买这种商品最划算应到的超市是
A.甲
B.乙
C.丙
D.乙或丙
(2019·期中·上海上海市杨浦区)甲、乙两人在环形跑道上练习跑步,已知环形跑道圈长
米,乙每秒跑
米,甲每秒跑
米.如果甲在乙前面
米处同时同向出发,那么经过
秒两人首次相遇?
A.
秒
B.
秒
C.
秒
D.
秒
(2020·专项)在
中,,,
边上的高
,则另一边
等于
A.
B.
C.
或
D.
或
(2020·真题·广西玉林市)观察下列按一定规律排列的
个数:,,,,,,,若最后三个数之和是
,则
等于
A.
B.
C.
D.
(2019·期末·河北石家庄市行唐县)点
,
在同一条数轴上,其中点
表示的数为
,若
,则
点在数轴上对应点是
A.
或
B.
或
C.
或
D.
(2018·期末·浙江嘉兴市秀洲区)某班有学生
人,参加文学社的人数是参加科学社的人数的
倍,既参加文学
社又参加科学社的人数是
人,既不参加文学社也不参加科学社的有
人,则参加科学
社但不参加文学社的人数是
A.
B.
C.
D.
二、填空题(30分)
(2020·同步练习·上海上海市)在梯形面积公式
中,如
,,,那么
.
(2019·期中·四川成都市锦江区)在平面直角坐标系中,已知
,点
是
轴上一点,若
为等腰三角形,则点
的坐标为
.
(2019·期末·河北石家庄市行唐县)如图,,
平分
,如果射线
上的点
满足
是等腰三角形,那么
的度数为
.
(2017·期末·浙江杭州市下城区)某单位购进A,B,C三种型号的笔记本
本,它们的单价分别是
元、
元和
元,共计花费
元,若其中有A种型号的笔记本
本,则B种型号的有
本.(结果用含
的代数式表示)
(2019·期中·河南郑州市金水区)如图,在
中,,,,点
在边
上,以
为折痕将
折叠得到
,边
与边
交于点
.若
为直角三角形,则
的长是
.
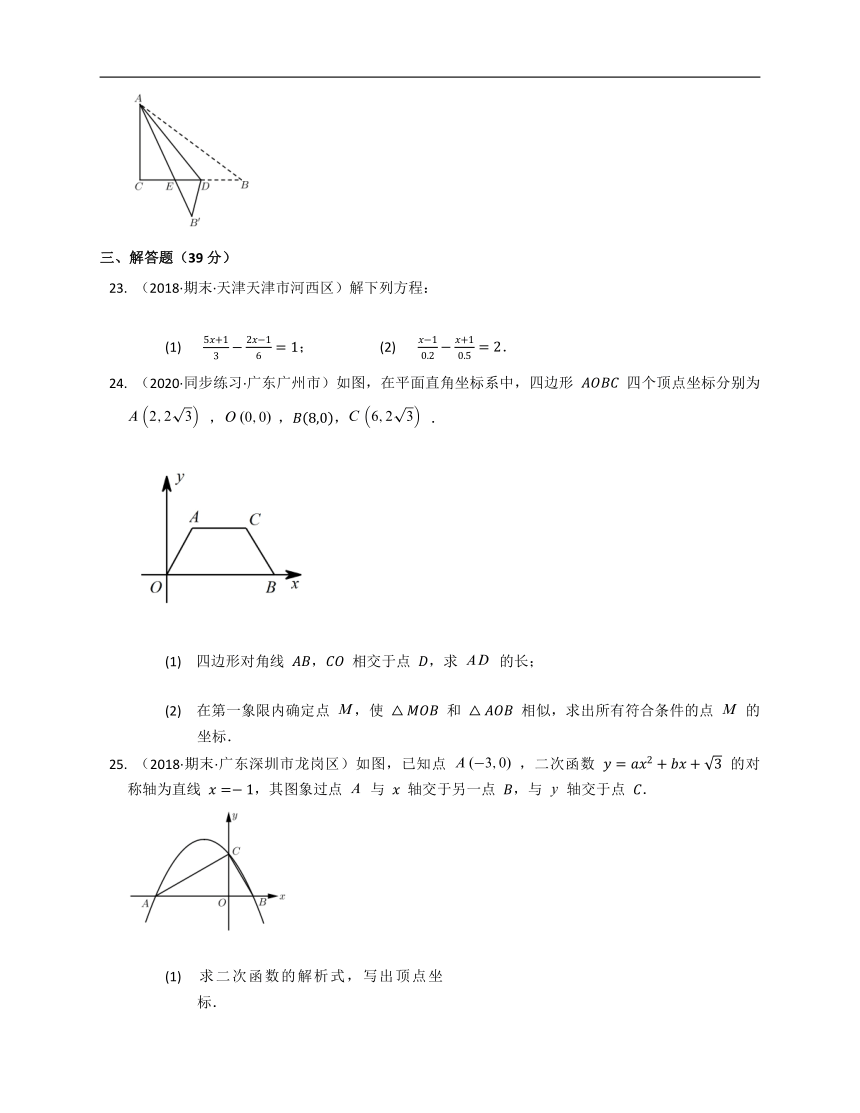
三、解答题(39分)
(2018·期末·天津天津市河西区)解下列方程:
(1)
;
(2)
.
(2020·同步练习·广东广州市)如图,在平面直角坐标系中,四边形
四个顶点坐标分别为
,,,.
(1)
四边形对角线
,
相交于点
,求
的长;
(2)
在第一象限内确定点
,使
和
相似,求出所有符合条件的点
的坐标.
(2018·期末·广东深圳市龙岗区)如图,已知点
,二次函数
的对称轴为直线
,其图象过点
与
轴交于另一点
,与
轴交于点
.
(1)
求二次函数的解析式,写出顶点坐标.
(2)
动点
,
同时从
点出发,均以每秒
个单位长度的速度分别沿
的
,
边上运动,设其运动的时间为
秒,当其中一个点到达终点时,另一个点也随之停止运动.连接
,将
沿
翻折,若点
恰好落在抛物线弧上的
处,试求
的值及点
的坐标.
(3)
在()的条件下,
为
的中点,试探究坐标轴上是否存在点
,使得以
,,
为顶点的三角形与
相似?如果存在,请求出点
的坐标;如果不存在,试说明理由.
答案
一、选择题
1.
【答案】C
【知识点】去分母
去括号
2.
【答案】A
【知识点】一元一次方程的概念
3.
【答案】D
【知识点】和差倍分
4.
【答案】B
【解析】A、设最小的数是
.
,
,
故本选项不符合题意;
B、设最小的数是
.
,
.
故本选项符合题意.
C、设最小的数是
.
,
,
故本选项不符合题意.
D、设最小的数是
.
,
,
故本选项不符合题意.
故选:B.
【知识点】和差倍分
5.
【答案】C
【解析】设点
到直线
的距离为
,
的面积为:.
当
在线段
运动时,此时
不断增大,
也不端增大;
当
在线段
上运动时,此时
不变,
也不变;
当
在线段
上运动时,此时
不断减小,
不断减少.
又
匀速行驶且
,
在线段
上运动的时间大于在线段
上运动的时间.
【知识点】图像法
6.
【答案】D
【知识点】等式的性质
7.
【答案】A
【解析】将
代入方程得
,解得
.
【知识点】含参一元一次方程的解法
8.
【答案】B
【知识点】一元一次方程的概念
9.
【答案】B
【解析】设需更换的新型节能灯有
盏,
则
,
解得
,
则需更换的新型节能灯有
盏.
【知识点】和差倍分
10.
【答案】D
【解析】设中间的数为
,则另
个数分别为:,,,,,,,,
.
A.当
时,,
,
是第
行第
个数,不可能为中间数,
选项A不符合题意;
B.当
时,,
不为整数,
选项B不符合题意;
C.当
时,,
,
是第
行第
个数,不可能为中间数,
选项C不符合题意;
D.当
时,,
,
是第
行第
个数,可以为中间数,
选项D符合题意.
【知识点】和差倍分
11.
【答案】C
【解析】设在这次买卖中原价都是
元,
则可列方程:解得:比较可知,第一件赚了
元,
第二件可列方程:解得:比较可知亏了
元,
两件相比则一共亏了
元.
故选:C.
【知识点】利润问题
12.
【答案】B
【知识点】利润问题
13.
【答案】D
【知识点】行程问题
14.
【答案】C
【知识点】勾股定理
15.
【答案】C
【解析】由题意,得第
个数为
,
那么
,
解得:,
故选:C.
【知识点】和差倍分
16.
【答案】B
【解析】当
点在
点右侧时,
,
点表示的数是
,
当
点在
点的左侧时,
,
点表示的数是
.
【知识点】数轴的概念
17.
【答案】D
【解析】设参加科学社但不参加文学社的人数是
人,则参加科学社的人数是
人,
参加文学社的人数是
人,
根据题意得:,
解得:.
【知识点】和差倍分
二、填空题
18.
【答案】
;
【知识点】去分母
去括号
19.
【答案】
,,,
;
【解析】有四个.如图.
由勾股定理,可得
.
在
轴上取
,则
为等腰三角形,;
在
轴上取
,则
为等腰三角形,;
在
轴上取
,则
为等腰三角形,.
是等腰直角三角形,其中,.
是有四个三角形是等腰三角形,符合条件的点有
,,,
这四个点.
故点
的坐标为:,,,.
【知识点】平面直角坐标系及点的坐标
20.
【答案】
或
或
;
【解析】
,
平分
,
,
①当
在
时,,
,
;
②当
在
点时,,
则
;
③当
在
时,,
则
;
故答案为:
或
或
.
【知识点】等边对等角
21.
【答案】
;
【解析】设B种型号的有
本,
根据题意得:,
解得:,
则B种型号的有
本;
故答案为:.
【知识点】和差倍分
22.
【答案】
或
;
【解析】()当
时,如图
所示:
由折叠得:,,
在
中,,
,,
,
,
,即
,
,,
,
设
,则
,
在
中,由勾股定理得:,
解得:,(舍去).
()当
时,此时点
与点
重合,如图
所示:
由折叠得,,
,
设
,则
,,
在
中,由勾股定理得:,
解得:.
【知识点】勾股定理之折叠问题
三、解答题
23.
【答案】
(1)
去分母,得去括号,得移项、合并同类项,得系数化为
,得
(2)
去分母,得去括号,得移项、合并同类项,得系数化为
,得
【知识点】去分母
去括号
24.
【答案】
(1)
(2)
点
位于点
上时,
与
相似,此时点
的坐标为
;
过点
作
的垂线交
的延长线于
,
与
相似,此时点
的坐标为
;
过点
作
的垂线交
的延长线于
,
与
相似,此时点
的坐标为
.
【知识点】综合判定、基本定理、等腰梯形
25.
【答案】
(1)
由题意得,
解得:
二次函数的解析式为
,
,其顶点坐标为
.
(2)
由题意知,,,,
,
又
,
是正三角形,
,,
将
沿
翻折后,,
,
,
,
若点
在抛物线上,
则有
,
化简得:,
,
,
此时,,,.
(3)
由题意可得
为直角三角形,
且
,,又
,
分二种情况讨论:
①当
在
轴上时,
过
作
交
轴于
,
则
,此时
,
过
作
轴于
,
则
,此时
.
在
轴上其他位置时,
三角形
不为直角三角形,不可能与
相似.
②同理,当
点在
轴上时,设
交
轴于
,
则
,此时
.
过
作
交
轴于
,
但
,则
与
不相似,
在
轴上其他位置时,
三角形
不为直角三角形,不可能与
相似.
综上,
的坐标为
,,.
【知识点】y=ax^2+bx+c的图象、两角分别相等、二次函数的解析式、坐标平面内图形轴对称变换、二次函数的顶点
一、选择题(51分)
(2017·期末·天津天津市河北区)方程
的解是
,则
的值是
A.
B.
C.
D.
(2019·期末·广东深圳市福田区)下列方程:①
;②
;③
;④
;⑤
,其中是一元一次方程的有
A.
个
B.
个
C.
个
D.以上答案都不对
(2020·同步练习)参加保险公司的医疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表:某人住院治疗后得到保险公司报销金额是
元,那么此人住院的医疗费是
A.
元
B.
元
C.
元
D.
元
(2019·期末·江苏苏州市张家港市)小淇在某月的日历中圈出相邻的三个数,算出它们的和是
,那么这三个数的位置可能是
A.
B.
C.
D.
(2019·期中·广东深圳市南山区)如图,在四边形
中,动点
从点
开始沿
的路径匀速前进到
为止.在这个过程中,
的面积
随时间
的变化关系用图象表示正确的是
A.
B.
C.
D.
(2019·单元测试·北京北京市朝阳区)下列说法错误的是
A.若
,则
B.若
,则
C.若
,则
D.若
,则
(2018·期中·北京北京市西城区)如果
是方程
的解,那么
的值是
A.
B.
C.
D.
(2020·专项·上海上海市闵行区)有下列四个等式:
①
;
②
;
③
;
④
.
其中一元一次方程有
A.
个
B.
个
C.
个
D.
个
(2020·同步练习)某道路一侧原有路灯
盏,相邻两盏灯的距离为
,,现计划全部更换为新型的节能灯,且相邻两盏灯的距离变为
,则需更换的新型节能灯有
A.
盏
B.
盏
C.
盏
D.
盏
(2018·期末)将正整数
至
按一定规律排列如图所示,从表中任取一个
的方框,方框中九个数的和可能是
A.
B.
C.
D.
(2019·期末·江苏徐州市铜山区)某个体商贩在一次买卖中,同时卖出两件上衣,售价都是
元,若按成本计,其中一件盈利
,另一件亏本
,在这次买卖中他
A.不赚不赔
B.赚
元
C.赔
元
D.赚
元
(2019·期中·广东广州市天河区)甲,乙,丙三家超市为了促销一种定价均为
元的商品,甲超市连续两次降价
,乙超市一次性降价
,丙超市第一次降价
,第二次降价
,此时顾客要购买这种商品最划算应到的超市是
A.甲
B.乙
C.丙
D.乙或丙
(2019·期中·上海上海市杨浦区)甲、乙两人在环形跑道上练习跑步,已知环形跑道圈长
米,乙每秒跑
米,甲每秒跑
米.如果甲在乙前面
米处同时同向出发,那么经过
秒两人首次相遇?
A.
秒
B.
秒
C.
秒
D.
秒
(2020·专项)在
中,,,
边上的高
,则另一边
等于
A.
B.
C.
或
D.
或
(2020·真题·广西玉林市)观察下列按一定规律排列的
个数:,,,,,,,若最后三个数之和是
,则
等于
A.
B.
C.
D.
(2019·期末·河北石家庄市行唐县)点
,
在同一条数轴上,其中点
表示的数为
,若
,则
点在数轴上对应点是
A.
或
B.
或
C.
或
D.
(2018·期末·浙江嘉兴市秀洲区)某班有学生
人,参加文学社的人数是参加科学社的人数的
倍,既参加文学
社又参加科学社的人数是
人,既不参加文学社也不参加科学社的有
人,则参加科学
社但不参加文学社的人数是
A.
B.
C.
D.
二、填空题(30分)
(2020·同步练习·上海上海市)在梯形面积公式
中,如
,,,那么
.
(2019·期中·四川成都市锦江区)在平面直角坐标系中,已知
,点
是
轴上一点,若
为等腰三角形,则点
的坐标为
.
(2019·期末·河北石家庄市行唐县)如图,,
平分
,如果射线
上的点
满足
是等腰三角形,那么
的度数为
.
(2017·期末·浙江杭州市下城区)某单位购进A,B,C三种型号的笔记本
本,它们的单价分别是
元、
元和
元,共计花费
元,若其中有A种型号的笔记本
本,则B种型号的有
本.(结果用含
的代数式表示)
(2019·期中·河南郑州市金水区)如图,在
中,,,,点
在边
上,以
为折痕将
折叠得到
,边
与边
交于点
.若
为直角三角形,则
的长是
.
三、解答题(39分)
(2018·期末·天津天津市河西区)解下列方程:
(1)
;
(2)
.
(2020·同步练习·广东广州市)如图,在平面直角坐标系中,四边形
四个顶点坐标分别为
,,,.
(1)
四边形对角线
,
相交于点
,求
的长;
(2)
在第一象限内确定点
,使
和
相似,求出所有符合条件的点
的坐标.
(2018·期末·广东深圳市龙岗区)如图,已知点
,二次函数
的对称轴为直线
,其图象过点
与
轴交于另一点
,与
轴交于点
.
(1)
求二次函数的解析式,写出顶点坐标.
(2)
动点
,
同时从
点出发,均以每秒
个单位长度的速度分别沿
的
,
边上运动,设其运动的时间为
秒,当其中一个点到达终点时,另一个点也随之停止运动.连接
,将
沿
翻折,若点
恰好落在抛物线弧上的
处,试求
的值及点
的坐标.
(3)
在()的条件下,
为
的中点,试探究坐标轴上是否存在点
,使得以
,,
为顶点的三角形与
相似?如果存在,请求出点
的坐标;如果不存在,试说明理由.
答案
一、选择题
1.
【答案】C
【知识点】去分母
去括号
2.
【答案】A
【知识点】一元一次方程的概念
3.
【答案】D
【知识点】和差倍分
4.
【答案】B
【解析】A、设最小的数是
.
,
,
故本选项不符合题意;
B、设最小的数是
.
,
.
故本选项符合题意.
C、设最小的数是
.
,
,
故本选项不符合题意.
D、设最小的数是
.
,
,
故本选项不符合题意.
故选:B.
【知识点】和差倍分
5.
【答案】C
【解析】设点
到直线
的距离为
,
的面积为:.
当
在线段
运动时,此时
不断增大,
也不端增大;
当
在线段
上运动时,此时
不变,
也不变;
当
在线段
上运动时,此时
不断减小,
不断减少.
又
匀速行驶且
,
在线段
上运动的时间大于在线段
上运动的时间.
【知识点】图像法
6.
【答案】D
【知识点】等式的性质
7.
【答案】A
【解析】将
代入方程得
,解得
.
【知识点】含参一元一次方程的解法
8.
【答案】B
【知识点】一元一次方程的概念
9.
【答案】B
【解析】设需更换的新型节能灯有
盏,
则
,
解得
,
则需更换的新型节能灯有
盏.
【知识点】和差倍分
10.
【答案】D
【解析】设中间的数为
,则另
个数分别为:,,,,,,,,
.
A.当
时,,
,
是第
行第
个数,不可能为中间数,
选项A不符合题意;
B.当
时,,
不为整数,
选项B不符合题意;
C.当
时,,
,
是第
行第
个数,不可能为中间数,
选项C不符合题意;
D.当
时,,
,
是第
行第
个数,可以为中间数,
选项D符合题意.
【知识点】和差倍分
11.
【答案】C
【解析】设在这次买卖中原价都是
元,
则可列方程:解得:比较可知,第一件赚了
元,
第二件可列方程:解得:比较可知亏了
元,
两件相比则一共亏了
元.
故选:C.
【知识点】利润问题
12.
【答案】B
【知识点】利润问题
13.
【答案】D
【知识点】行程问题
14.
【答案】C
【知识点】勾股定理
15.
【答案】C
【解析】由题意,得第
个数为
,
那么
,
解得:,
故选:C.
【知识点】和差倍分
16.
【答案】B
【解析】当
点在
点右侧时,
,
点表示的数是
,
当
点在
点的左侧时,
,
点表示的数是
.
【知识点】数轴的概念
17.
【答案】D
【解析】设参加科学社但不参加文学社的人数是
人,则参加科学社的人数是
人,
参加文学社的人数是
人,
根据题意得:,
解得:.
【知识点】和差倍分
二、填空题
18.
【答案】
;
【知识点】去分母
去括号
19.
【答案】
,,,
;
【解析】有四个.如图.
由勾股定理,可得
.
在
轴上取
,则
为等腰三角形,;
在
轴上取
,则
为等腰三角形,;
在
轴上取
,则
为等腰三角形,.
是等腰直角三角形,其中,.
是有四个三角形是等腰三角形,符合条件的点有
,,,
这四个点.
故点
的坐标为:,,,.
【知识点】平面直角坐标系及点的坐标
20.
【答案】
或
或
;
【解析】
,
平分
,
,
①当
在
时,,
,
;
②当
在
点时,,
则
;
③当
在
时,,
则
;
故答案为:
或
或
.
【知识点】等边对等角
21.
【答案】
;
【解析】设B种型号的有
本,
根据题意得:,
解得:,
则B种型号的有
本;
故答案为:.
【知识点】和差倍分
22.
【答案】
或
;
【解析】()当
时,如图
所示:
由折叠得:,,
在
中,,
,,
,
,
,即
,
,,
,
设
,则
,
在
中,由勾股定理得:,
解得:,(舍去).
()当
时,此时点
与点
重合,如图
所示:
由折叠得,,
,
设
,则
,,
在
中,由勾股定理得:,
解得:.
【知识点】勾股定理之折叠问题
三、解答题
23.
【答案】
(1)
去分母,得去括号,得移项、合并同类项,得系数化为
,得
(2)
去分母,得去括号,得移项、合并同类项,得系数化为
,得
【知识点】去分母
去括号
24.
【答案】
(1)
(2)
点
位于点
上时,
与
相似,此时点
的坐标为
;
过点
作
的垂线交
的延长线于
,
与
相似,此时点
的坐标为
;
过点
作
的垂线交
的延长线于
,
与
相似,此时点
的坐标为
.
【知识点】综合判定、基本定理、等腰梯形
25.
【答案】
(1)
由题意得,
解得:
二次函数的解析式为
,
,其顶点坐标为
.
(2)
由题意知,,,,
,
又
,
是正三角形,
,,
将
沿
翻折后,,
,
,
,
若点
在抛物线上,
则有
,
化简得:,
,
,
此时,,,.
(3)
由题意可得
为直角三角形,
且
,,又
,
分二种情况讨论:
①当
在
轴上时,
过
作
交
轴于
,
则
,此时
,
过
作
轴于
,
则
,此时
.
在
轴上其他位置时,
三角形
不为直角三角形,不可能与
相似.
②同理,当
点在
轴上时,设
交
轴于
,
则
,此时
.
过
作
交
轴于
,
但
,则
与
不相似,
在
轴上其他位置时,
三角形
不为直角三角形,不可能与
相似.
综上,
的坐标为
,,.
【知识点】y=ax^2+bx+c的图象、两角分别相等、二次函数的解析式、坐标平面内图形轴对称变换、二次函数的顶点
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
