北师大版九年级数学下册 2.5 二次函数与一元二次方程 同步测试题(word版,有答案)
文档属性
| 名称 | 北师大版九年级数学下册 2.5 二次函数与一元二次方程 同步测试题(word版,有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 335.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 13:10:00 | ||
图片预览

文档简介
10617200107442001231900002.5 二次函数与一元二次方程 同步测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 在平面直角坐标系中,抛物线y=x2-1与x轴的交点的个数是( )
A.3个 B.2个 C.1个 D.0个
?
2. 二次函数y=kx2-6x+7的图象过点(1,?2),且与x轴有两个交点A(x1,?0),B(x2,?0),则x1x2的值是( )
A.1 B.3 C.6 D.7
?
3. 如图,二次函数y1=ax2+bx+c和一次函数y2=kx+b的图象交于A(1,?0),B(-2,?-3)两点,若y1>y2,则x的取值范围是( )
A.x<-2 B.-21 D.x<-2或x>1
?
4. 抛物线y=x2+3x-4与x轴交点的个数为( )
A.1个 B.2个 C.0个 D.3个
?
5. 抛物线y=-3x2+2x-1与坐标轴的交点个数为( )
A.0个 B.1个 C.2个 D.3个
?
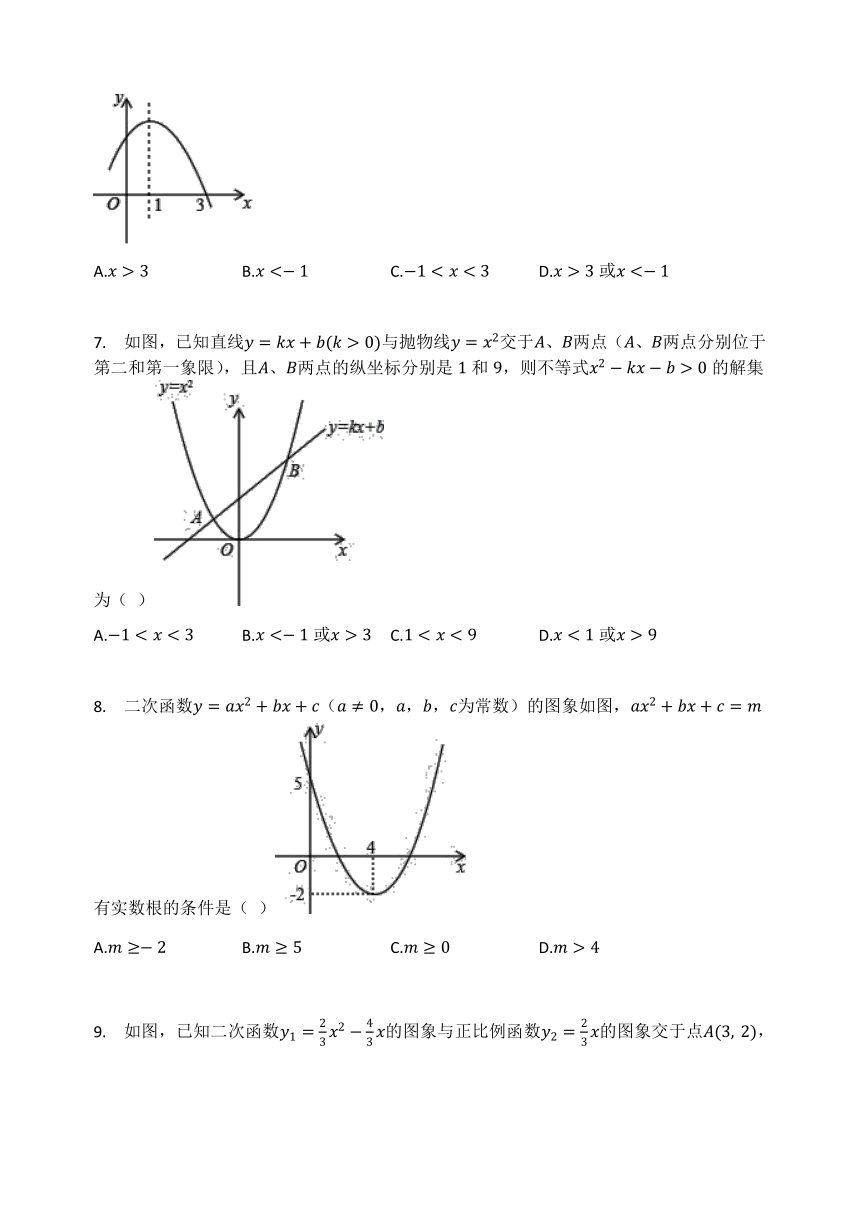
6. 如图,是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
A.x>3 B.x<-1 C.-13或x<-1
?
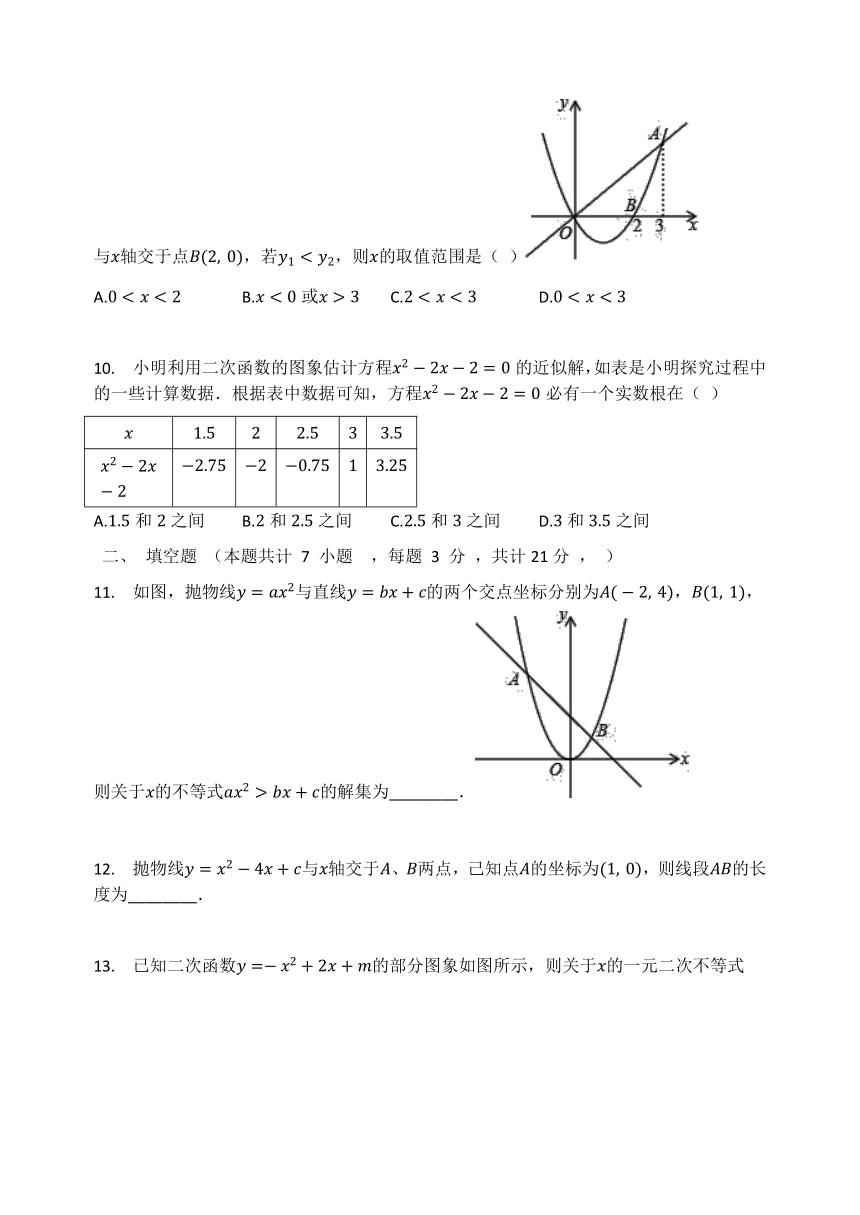
7. 如图,已知直线y=kx+b(k>0)与抛物线y=x2交于A、B两点(A、B两点分别位于第二和第一象限),且A、B两点的纵坐标分别是1和9,则不等式x2-kx-b>0的解集为( )
A.-13 C.19
?
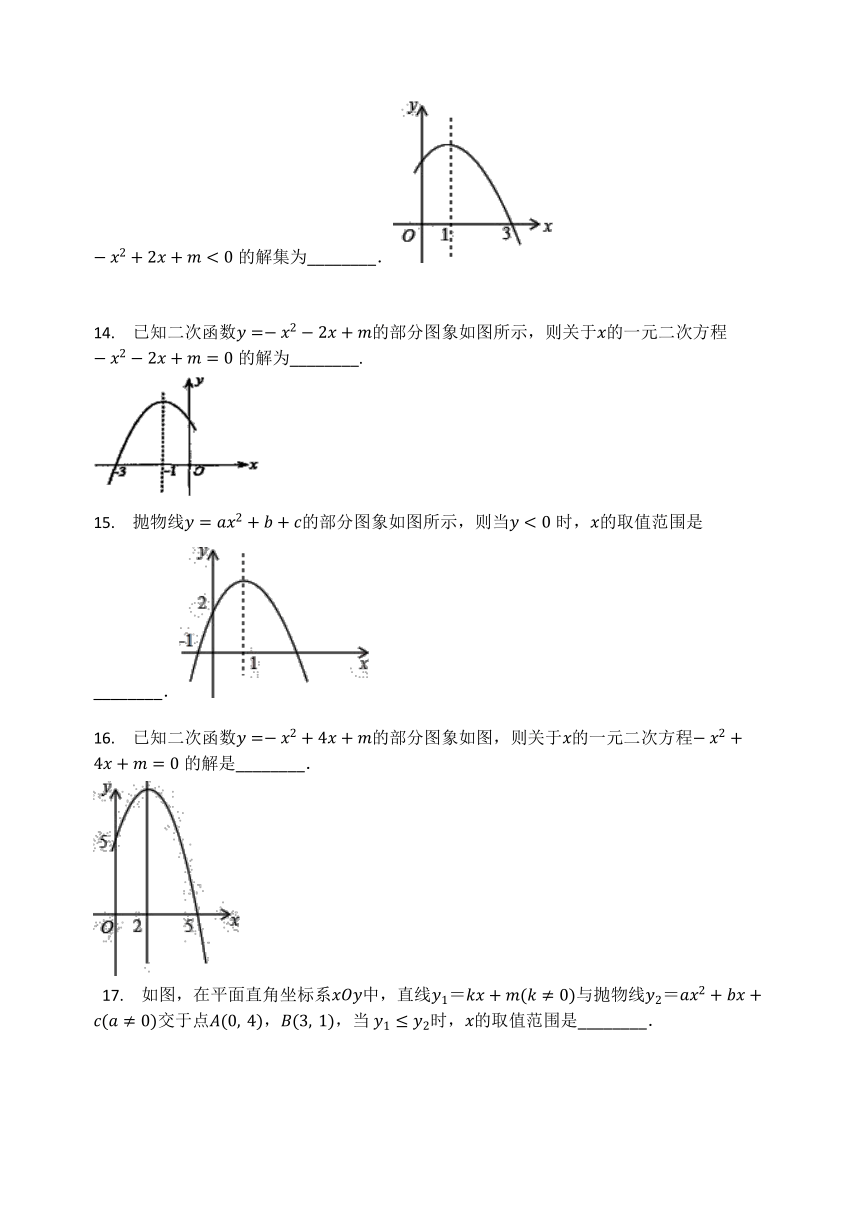
8. 二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象如图,ax2+bx+c=m有实数根的条件是( )
A.m≥-2 B.m≥5 C.m≥0 D.m>4
?
9. 如图,已知二次函数y1=23x2-43x的图象与正比例函数y2=23x的图象交于点A(3,?2),与x轴交于点B(2,?0),若y1 A.03 C.2?
10. 小明利用二次函数的图象估计方程x2-2x-2=0的近似解,如表是小明探究过程中的一些计算数据.根据表中数据可知,方程x2-2x-2=0必有一个实数根在( )
x
1.5
2
2.5
3
3.5
x2-2x-2
-2.75
-2
-0.75
1
3.25
A.1.5和2之间 B.2和2.5之间 C.2.5和3之间 D.3和3.5之间
二、 填空题 (本题共计 7 小题 ,每题 3 分 ,共计21分 , ) ?
11. 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,?4),B(1,?1),则关于x的不等式ax2>bx+c的解集为________.
?
12. 抛物线y=x2-4x+c与x轴交于A、B两点,己知点A的坐标为(1,?0),则线段AB的长度为________.
?
13. 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次不等式-x2+2x+m<0的解集为________.
?
14. 已知二次函数y=-x2-2x+m的部分图象如图所示,则关于x的一元二次方程-x2-2x+m=0的解为________.
15. 抛物线y=ax2+b+c的部分图象如图所示,则当y<0时,x的取值范围是________. ?
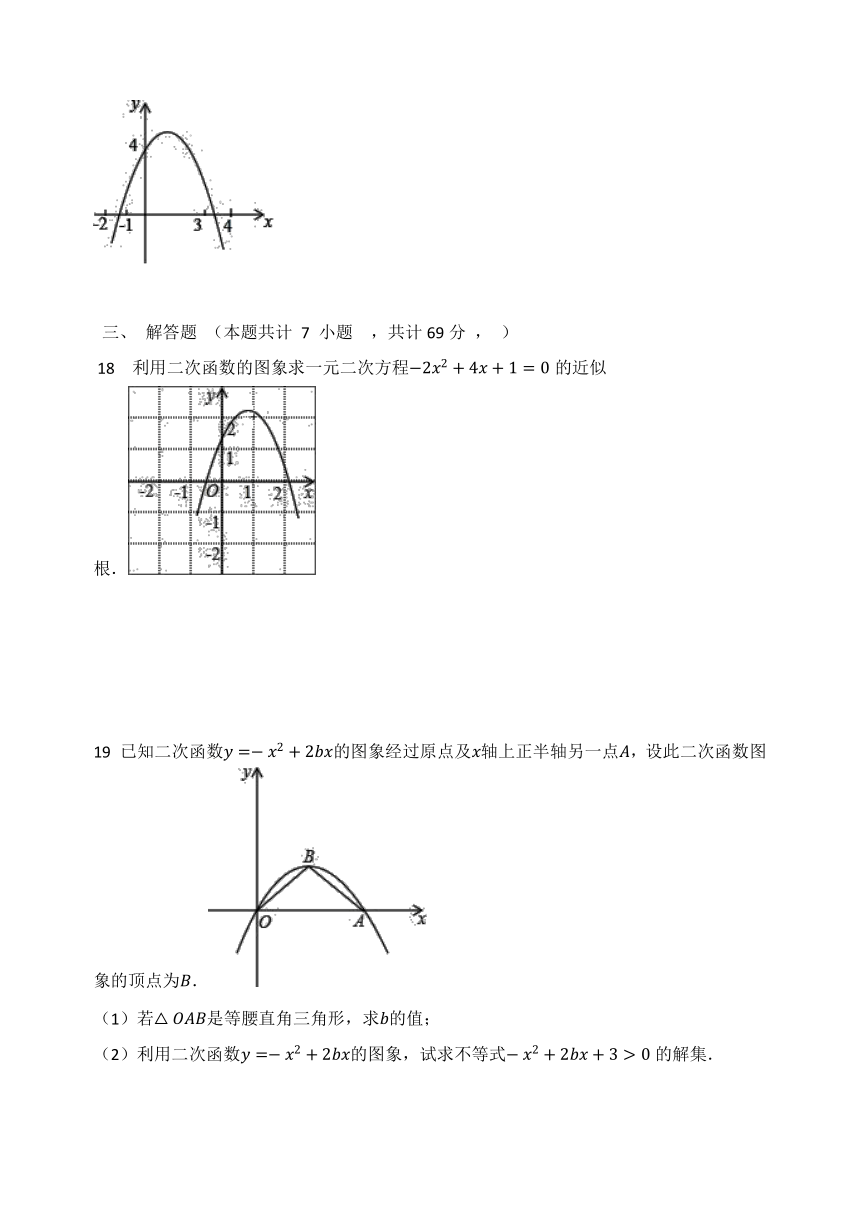
16. 已知二次函数y=-x2+4x+m的部分图象如图,则关于x的一元二次方程-x2+4x+m=0的解是________.
17. 如图,在平面直角坐标系xOy中,直线y1=kx+m(k≠0)与抛物线y2=ax2+bx+c(a≠0)交于点A(0,?4),B(3,?1),当?y1≤y2时,x的取值范围是________.
三、 解答题 (本题共计 7 小题 ,共计69分 , )
?18 利用二次函数的图象求一元二次方程-2x2+4x+1=0的近似根.
?
19 已知二次函数y=-x2+2bx的图象经过原点及x轴上正半轴另一点A,设此二次函数图象的顶点为B.
(1)若△OAB是等腰直角三角形,求b的值;
(2)利用二次函数y=-x2+2bx的图象,试求不等式-x2+2bx+3>0的解集.
?
20 已知二次函数y=x2-4x-5,画出这个二次函数的图象,根据图象回答下列问题:
(1)方程x2-4x-5=0的解是什么?
(2)x取什么值时,函数值大于0?x取什么值时,函数值小于0?
?
21 如图,抛物线y=-12x2+bx+c 与轴交于点A,B,与y轴交于点C,直线y=-12x+2 经过点 A,C.
(1)求抛物线的解析式.
(2)点P为直线AC上方抛物线上一动点上.
①连结PO,交AC于点E,求?PEEO??的最大值.
②过点P作PF⊥AC垂足为点F,连结PC,是否存在点P,使△PFC中的一个角等于∠CAB的2倍?
若存在,请直接写出点P的坐标;若不存在,请说明理由.
?
22. 如图,二次函数y=x2-2x-3的图象与两坐标轴分别交于A,B,C三点,一次函数的图象与抛物线交于B,C两点.
(1)求点A,B,C的坐标;
(2)当两函数的函数值都随着x的增大而增大,求x的取值范围;
(3)当自变量x满足什么范围时,一次函数值大于二次函数值.
?
23 我们可以用如下方法解不等式(x-1)(x+1)>0.
第一步:画出函数y=(x-1)(x+1)的图象;
第二步:找出图象与x轴的交点坐标,即交点坐标为(1,?0),(-1,?0);
第三步:根据图象可知,在x<-1或x>1时,y的值大于0.因此可得不等式(x-1)(x+1)>0的解集为x<-1或x>1.
请你仿照上述方法,求不等式x2-4<0的解集.
?
24 在平面直角坐标系中,抛物线y=x2+bx+c经过A(-1,0)、B(1,0)、C三点, 且C点为抛物线与y轴的交点.
(1)求抛物线的表达式;
(2)连接BC,过点A作AP//BC交抛物线于点P,求以点A、P、B、C为顶点的四边形的面积;
(3)在(2)的条件下,在x轴上方的抛物线上是“ 否存在一点M,过M作MG⊥x轴于点G,使以A,M,G三点为顶点的三角形与△PCA相似? 若存在,求出点M的坐标;若不存在,请说明理由.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
【解答】
解:当y=0时,x2-1=0,
∵ Δ=02-4×1×(-1)=4>0,
∴ 方程x2-1=0有两个不相等的实数根,
即抛物线y=x2-1与x轴有两个交点.
故选B.
2.
【答案】
D
【解答】
解:
∵ 二次函数过点(1,?2),
∴ k-6+7=2,解得k=1,
∴ 抛物线解析式为y=x2-6x+7,
令y=可得x2-6x+7=0,
由题意可知x1和x2是该方程的两根,
∴ x1x2=7,
故选D.
3.
【答案】
D
【解答】
解:观察图象可知:抛物线y1与直线y2的交点横坐标是-2,1,
故当x<-2或x>1时,y1>y2.
故选:D.
4.
【答案】
B
【解答】
解:当与x轴相交时,函数值为0.即x2+3x-4=0,
△=b2-4ac=32-4×1×(-4)=25>0,
∴ 有2个不相等的实数根,
∴ 抛物线y=x2+3x-4与x轴有2个交点,
故选:B.
5.
【答案】
B
【解答】
解:∵ △=22-4×(-3)×(-1)=-8<0,
∴ 抛物线与x轴没有交点,
而抛物线y=-3x2+2x-1与y轴的交点为(0,?-1),
∴ 抛物线y=-3x2+2x-1与坐标轴的交点个数为1.
故选B.
6.
【答案】
D
【解答】
抛物线与x轴的另外一个交点的坐标为:(-1,?0),
从图象看,不等式ax2+bx+c<0的解集是:x>3或x<-1,
7.
【答案】
B
【解答】
解:由x2-kx-b>0得x2>kx+b,
∵ A、B两点的纵坐标分别是1和9,
∴ 点A的横坐标为-1,点B的横坐标为3,
当x<-1或x>3时,抛物线图象在直线图象上方,
故不等式x2-kx-b>0的解集为x<-1或x>3.
故选B.
8.
【答案】
A
【解答】
解:一元二次方程ax2+bx+c=m有实数根,
可以理解为y=ax2+bx+c和y=m有交点,
可见,m≥-2,
故选:A.
9.
【答案】
D
【解答】
解:如图所示:若y1此时x的取值范围是:0故选:D.
10.
【答案】
C
【解答】
解:根据表格得,当2.5则方程x2-2x-2=0必有一个实数根在2.5和3之间.
故选C.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
11.
【答案】
x>1或x<-2
【解答】
解:∵ 抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,?4),B(1,?1),
∴ 关于x的不等式ax2>bx+c的解集为x>1或x<-2,
故答案为:x>1或x<-2.
12.
【答案】
2
【解答】
解:∵ 抛物线y=x2-4x+c=(x-2)2-4+c,
∴ 抛物线的对称轴为直线x=2,
∵ 点A的坐标为(1,?0),
∴ 点B的坐标为(3,?0),
∴ 线段AB=3-1=2,
故答案为2.
13.
【答案】
x<-1或x>3
【解答】
解:由图可知,对称轴为直线x=1,
所以,二次函数图象与x轴的另一个交点坐标为(-1,?0),
所以,-x2+2x+m<0的解集为x<-1或x>3.
故答案为:x<-1或x>3.
14.
【答案】
x1=-3,x2=1
【解答】
解:由图象可得,
二次函数y=-x2-2x+m与x轴的一个交点为(-3,0),且对称轴为x=-1,
所以与x轴的另一个交点为(1,0),
所以关于x的一元二次方程-x2-2x+m=0的解为
二次函数y=-x2-2x+m与x轴的交点的横坐标,
即x1=-3,x2=1.
故答案为:x1=-3,x2=1.
15.
【答案】
x<-1或x>3
【解答】
解:∵ 抛物线与x轴的一个交点坐标是(-1,?0),对称轴是直线x=1,
∴ 抛物线与x轴另一交点的坐标是(3,?0),
∴ 当y<0时,x<-1或x>3.
故答案为:x<-1或x>3.
16.
【答案】
x1=-1,x2=5
【解答】
解:根据图示知,
二次函数y=-x2+4x+m的对称轴为x=2,与x轴的一个交点为(5,?0),
根据抛物线的对称性知,抛物线与x轴的另一个交点横坐标与点(5,?0)关于对称轴对称,即x=-1,
则另一交点坐标为(-1,?0)
则当x=-1或x=5时,函数值y=0,
即-x2+4x+m=0,
故关于x的一元二次方程-x2+4x+m=0的解为
x1=-1,x2=5.
故答案为:x1=-1,x2=5.
17.
【答案】
0≤x≤3
【解答】
∵ 两函数图象交于点A(0,?4),B(3,?1),
∴ 当?y1≤y2时,x的取值范围是0≤x≤3.
18.
【答案】
4
【解答】
解:①由y=ax2+bx+c与x轴的交点坐标为(-2,?0)得:
a×(-2)2+b×(-2?)+c=0,
即4a-2b+c=0,
所以①正确;
②由图象开口向下知a<0,
由y=ax2+bx+c与x轴的另一个交点
坐标为(x1,?0?),且1则该抛物线的对称轴为x=-b2a=(-2)+x12>-12,
即ba<1,
由a<0,两边都乘以a得:b>a,
∵ a<0,对称轴x=-b2a<0,
∴ b<0,
∴ a③由一元二次方程根与系数的关系知x1.x2=ca<-2,
结合a<0得2a+c>0,
所以结论③正确,
④由4a-2b+c=0得2a-b=-c2,
而0∴ -1<-c2<0,
∴ -1<2a-b<0,
∴ 2a-b+1>0,所以结论④正确.
故答案为:4.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
19.
【答案】
解:如图,
图象与x轴的交点坐标是(-0.2,?0)(2.2,?0),
一元二次方程-2x2+4x+1=0的近似根x1≈-0.2,x2≈2.2.
【解答】
解:如图,
图象与x轴的交点坐标是(-0.2,?0)(2.2,?0),
一元二次方程-2x2+4x+1=0的近似根x1≈-0.2,x2≈2.2.
20.
【答案】
解:(1)∵ △OAB是等腰直角三角形,
∴ 设B点横坐标为:a,则OA=2a,
故B点纵坐标为;(a,?a),
则a=-a2+2ba,-2b2×(-1)=a,则a=b,
故整理得:a2-a=0,
解得:a1=0(不合题意舍去),a2=1,
故b=1;
(2)由(1)得:y=-x2+2x,
则y=-x2+2x+3是y=-x2+2x向上平移3个单位得到的,
故y=0时,0=-x2+2x+3
解得:x1=-1,x2=3,
如图所示:不等式-x2+2bx+3>0的解集为:-1【解答】
解:(1)∵ △OAB是等腰直角三角形,
∴ 设B点横坐标为:a,则OA=2a,
故B点纵坐标为;(a,?a),
则a=-a2+2ba,-2b2×(-1)=a,则a=b,
故整理得:a2-a=0,
解得:a1=0(不合题意舍去),a2=1,
故b=1;
(2)由(1)得:y=-x2+2x,
则y=-x2+2x+3是y=-x2+2x向上平移3个单位得到的,
故y=0时,0=-x2+2x+3
解得:x1=-1,x2=3,
如图所示:不等式-x2+2bx+3>0的解集为:-121.
【答案】
解:给出x的部分值,求出相应的y值,
列成如下表格:
按照表格中的数据在平面直角坐标系内,作出5个点:
A(-1,?0)、C(0,?5)、D(2,?-9)、E(4,?-5)、B(5,?0),
用平滑的曲线将5个点连接起来,即得函数的图象.
(1)由图象可知:x1=-1,x2=5.
(2)由图象可知:当x<-1或x>5时,y>0;
当-1【解答】
解:给出x的部分值,求出相应的y值,
列成如下表格:
按照表格中的数据在平面直角坐标系内,作出5个点:
A(-1,?0)、C(0,?5)、D(2,?-9)、E(4,?-5)、B(5,?0),
用平滑的曲线将5个点连接起来,即得函数的图象.
(1)由图象可知:x1=-1,x2=5.
(2)由图象可知:当x<-1或x>5时,y>0;
当-122.
【答案】
解:(1)对于y=-12x+2,
当x=0时,y=2,
当y=0时,x=4,
∴ A(4,0),C(0,2).
∵ 抛物线y=-12x2+bx+c经过点A(4,0),C(0,2),
∴ -8+4b+c=0,c=2,
解得b=-32,c=2.
故抛物线的解析式为y=-12x2+32x+2.
(2)①如图(1),过点P作PN⊥x轴于点N,交直线AC于点M,
则PN//y轴,
∴ ∠PME=∠OCE,
又∵ ∠PEM=∠OEC,
∴ △PEM?△OEC,
∴ PEEO=PMOC.
∵ C(0,2),
∴ OC=2.
设点P的坐标为(t,-12t2+32t+2),
则点Mt,-12t+2,
∴ PM=-12t2+32t+2--12t+2=-12t2+2t,
∴ PEEO=-14t2+t=-14(t-2)2+1.
∵ -14<0,0∴ 当t=2时,PEEO有最大值1.
②存在,
易得∠PFC≠2∠CAB,分以下两种情况.
当∠PCF=2∠CAB时,如图(2),在y轴上取点D,使点C于点D关于x轴对称,连结AD,
则∠CAB=∠DAB,点D的坐标为(0,-2).
∴ ∠PCF=∠CAD,
∴ PC//AD,
设直线AD的解析式为y=kx+d,
则d=-2,4k+d=0,
解得k=12,d=-2.
故直线AD的解析式为y=12x-2,直线PC的解析式为y=12x+2.
令-12x2+32x+2=12x+2,
整理,得x2-2x=0,
解得x1=0(不合题意,舍去),x2=2.
当x=2时,y=-12×22+32×2+2=3,
故点P的坐标为(2,3).
当∠CPF=2∠CAB时,如图(3),过点C作CH⊥AD于点H,过点A作AG⊥CP,交CP的延长线于点G,
易得∠ACP=∠ACH,
从而可得AG=AH,CG=CH.
由勾股定理可得AC=AD=25,
由三角形面积公式可得12AD?CH=12CD?OA,
即12×25CH=12×4×4,
解得CH=85.
由勾股定理得AH=65,
∴ CG=85,AG=65.
过点G作GQ⊥x轴于点Q,作GR⊥y轴于点R,
设点G的坐标为(m,n),则GH=m,GQ=n.
在Rt△GAQ和Rt△GCR中,
由勾股定理得(4-m)2+n2=652,m2+(n-2)2=852,
解得m1=8825,n1=6625,m2=85,n2=-65,(不合题意,舍去)
设直线CG的解析式为y=k1x+e,
将C(0,2) G8825,6625分别代入,
得e=2,8825k1+e=6625,
解得k1=211,e=2,
故直线CG的解析式为y=211x+2.
令-12x2+32x+2=211x+2,
整理,得11x2-29x=0,
解得x1=2911,x2=0,(不合题意,舍去).
在y=211x+2,
当x=2911时,y=211×2911+2=300121,
故点P的坐标为2911,300121.
综上,点P的坐标为(2,3)或2911,300121.
【解答】
解:(1)对于y=-12x+2,
当x=0时,y=2,
当y=0时,x=4,
∴ A(4,0),C(0,2).
∵ 抛物线y=-12x2+bx+c经过点A(4,0),C(0,2),
∴ -8+4b+c=0,c=2,
解得b=-32,c=2.
故抛物线的解析式为y=-12x2+32x+2.
(2)①如图(1),过点P作PN⊥x轴于点N,交直线AC于点M,
则PN//y轴,
∴ ∠PME=∠OCE,
又∵ ∠PEM=∠OEC,
∴ △PEM?△OEC,
∴ PEEO=PMOC.
∵ C(0,2),
∴ OC=2.
设点P的坐标为(t,-12t2+32t+2),
则点Mt,-12t+2,
∴ PM=-12t2+32t+2--12t+2=-12t2+2t,
∴ PEEO=-14t2+t=-14(t-2)2+1.
∵ -14<0,0∴ 当t=2时,PEEO有最大值1.
②存在,
易得∠PFC≠2∠CAB,分以下两种情况.
当∠PCF=2∠CAB时,如图(2),在y轴上取点D,使点C于点D关于x轴对称,连结AD,
则∠CAB=∠DAB,点D的坐标为(0,-2).
∴ ∠PCF=∠CAD,
∴ PC//AD,
设直线AD的解析式为y=kx+d,
则d=-2,4k+d=0,
解得k=12,d=-2.
故直线AD的解析式为y=12x-2,直线PC的解析式为y=12x+2.
令-12x2+32x+2=12x+2,
整理,得x2-2x=0,
解得x1=0(不合题意,舍去),x2=2.
当x=2时,y=-12×22+32×2+2=3,
故点P的坐标为(2,3).
当∠CPF=2∠CAB时,如图(3),过点C作CH⊥AD于点H,过点A作AG⊥CP,交CP的延长线于点G,
易得∠ACP=∠ACH,
从而可得AG=AH,CG=CH.
由勾股定理可得AC=AD=25,
由三角形面积公式可得12AD?CH=12CD?OA,
即12×25CH=12×4×4,
解得CH=85.
由勾股定理得AH=65,
∴ CG=85,AG=65.
过点G作GQ⊥x轴于点Q,作GR⊥y轴于点R,
设点G的坐标为(m,n),则GH=m,GQ=n.
在Rt△GAQ和Rt△GCR中,
由勾股定理得(4-m)2+n2=652,m2+(n-2)2=852,
解得m1=8825,n1=6625,m2=85,n2=-65,(不合题意,舍去)
设直线CG的解析式为y=k1x+e,
将C(0,2)?G8825,6625分别代入,
得e=2,8825k1+e=6625,
解得k1=211,e=2,
故直线CG的解析式为y=211x+2.
令-12x2+32x+2=211x+2,
整理,得11x2-29x=0,
解得x1=2911,x2=0,(不合题意,舍去).
在y=211x+2,
当x=2911时,y=211×2911+2=300121,
故点P的坐标为2911,300121.
综上,点P的坐标为(2,3)或2911,300121.
23.
【答案】
解:(1)∵ 令x=0,则y=-3,
∴ C(0,?-3).
∵ 令y=0,则x2-2x-3=0,解得x=-1或x=3,
∴ A(-1,?0),B(3,?0).
(2)∵ 由(1)知,A(-1,?0),B(3,?0),
∴ 抛物线的对称轴为直线x=3-12=1,
∴ 当x>1时,两函数的函数值都随着x的增大而增大;
(3)∵ 由函数图象可知,当0∴ 当0【解答】
解:(1)∵ 令x=0,则y=-3,
∴ C(0,?-3).
∵ 令y=0,则x2-2x-3=0,解得x=-1或x=3,
∴ A(-1,?0),B(3,?0).
(2)∵ 由(1)知,A(-1,?0),B(3,?0),
∴ 抛物线的对称轴为直线x=3-12=1,
∴ 当x>1时,两函数的函数值都随着x的增大而增大;
(3)∵ 由函数图象可知,当0∴ 当024.
【答案】
解:如图,不等式x2-4<0的解集是-2【解答】
解:如图,不等式x2-4<0的解集是-225.
【答案】
解:(1)∵ 抛物线y=x2+bx+c经过点A(-1,0)、B(1,0),
∴ 1-b+c=01+b+c=0,解得b=0c=-1,
∴ 抛物线额的表达式为y=x2-1;
(2)将x=0代入y=x2-1,得y=-1,
∴ C(0,-1),OC=1
∵ OA=OB=OC=1
∴ ∠BAC=∠ACO=∠BCO=∠ABC=45?
∵ AP//BC
∴ ∠PAB=∠ABC=45?,
如解图①,过点P作PE⊥x轴于点E,则△APE为等腰直角三角形,
令OE=a,则PE=AE=a+1,
∴ P(a,a+1),
∵ 点P在抛物线y=x2-1上,
∴ a+1=a2-1,
解得a1=2,a2=-1(不合题意,舍去),
∴ PE=3,
∴ S四边形ACBP=SΔABC+S△ABP=12AB?OC+12AB?PE=12×2×1+12×2×3=4;
(3)存在,
如解图②,
∵ ∠PAB=∠BAC=45?,
∴ PA⊥AC,
∴ ∠MGA=∠PAC=90?,
在Rt△AOC中,OA=OC=1,
∴ AC=OA2+OC2=2,
在Rt△PAE中,AE=PE=3,
∴ AP=AE2+PE2=32,
设M点横坐标为m,则M(m,m2-1),
∵ 点M在x轴上方抛物线上,
∴ m2-1>0,
∴ m<-1或m>1,
①当M在y轴左侧时,则m<-1.
(i)当△AMG?△PCA时,有AGPA=MGCA,
∵ AG=-m-1,MG=m2-1,
∴ -m-132=m2-12,
解得m1=-1(舍去),m2=23(舍去);
(ii)当△MAG?△PCA时,有AGCA=MGPA,
即-m-12=m2-132,
解得m1=-1(舍去),m2=-2,
∴ M(-2,3);
②点M在y轴右侧时,则m>1,
(i)当△AMG?△PCA时,有AGPA=MGCA,
∵ AG=m+1,MG=m2-1,
∴ m+132=m2-12,解得m1=-1?(舍去),m2=43,
∴ M(43,79);
(ii)当△MAG?△PCA时,有AGCA=MGPA,
即m+12=m2-132,解得m1=-1(舍去),m2=4,
∴ M(4,15),
综上所述,存在点M,使以A,M,G三点为顶点的三角形与△PCA相似,点M的坐标为(-2,3)或(43,79)或(4,15).
【解答】
解:(1)∵ 抛物线y=x2+bx+c经过点A(-1,0)、B(1,0),
∴ 1-b+c=01+b+c=0,解得b=0c=-1,
∴ 抛物线额的表达式为y=x2-1;
(2)将x=0代入y=x2-1,得y=-1,
∴ C(0,-1),OC=1
∵ OA=OB=OC=1
∴ ∠BAC=∠ACO=∠BCO=∠ABC=45?
∵ AP//BC
∴ ∠PAB=∠ABC=45?,
如解图①,过点P作PE⊥x轴于点E,则△APE为等腰直角三角形,
令OE=a,则PE=AE=a+1,
∴ P(a,a+1),
∵ 点P在抛物线y=x2-1上,
∴ a+1=a2-1,
解得a1=2,a2=-1(不合题意,舍去),
∴ PE=3,
∴ S四边形ACBP=SΔABC+S△ABP=12AB?OC+12AB?PE=12×2×1+12×2×3=4;
(3)存在,
如解图②,
∵ ∠PAB=∠BAC=45?,
∴ PA⊥AC,
∴ ∠MGA=∠PAC=90?,
在Rt△AOC中,OA=OC=1,
∴ AC=OA2+OC2=2,
在Rt△PAE中,AE=PE=3,
∴ AP=AE2+PE2=32,
设M点横坐标为m,则M(m,m2-1),
∵ 点M在x轴上方抛物线上,
∴ m2-1>0,
∴ m<-1或m>1,
①当M在y轴左侧时,则m<-1.
(i)当△AMG?△PCA时,有AGPA=MGCA,
∵ AG=-m-1,MG=m2-1,
∴ -m-132=m2-12,
解得m1=-1(舍去),m2=23(舍去);
(ii)当△MAG?△PCA时,有AGCA=MGPA,
即-m-12=m2-132,
解得m1=-1(舍去),m2=-2,
∴ M(-2,3);
②点M在y轴右侧时,则m>1,
(i)当△AMG?△PCA时,有AGPA=MGCA,
∵ AG=m+1,MG=m2-1,
∴ m+132=m2-12,解得m1=-1?(舍去),m2=43,
∴ M(43,79);
(ii)当△MAG?△PCA时,有AGCA=MGPA,
即m+12=m2-132,解得m1=-1(舍去),m2=4,
∴ M(4,15),
综上所述,存在点M,使以A,M,G三点为顶点的三角形与△PCA相似,点M的坐标为(-2,3)或(43,79)或(4,15).
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 在平面直角坐标系中,抛物线y=x2-1与x轴的交点的个数是( )
A.3个 B.2个 C.1个 D.0个
?
2. 二次函数y=kx2-6x+7的图象过点(1,?2),且与x轴有两个交点A(x1,?0),B(x2,?0),则x1x2的值是( )
A.1 B.3 C.6 D.7
?
3. 如图,二次函数y1=ax2+bx+c和一次函数y2=kx+b的图象交于A(1,?0),B(-2,?-3)两点,若y1>y2,则x的取值范围是( )
A.x<-2 B.-2
?
4. 抛物线y=x2+3x-4与x轴交点的个数为( )
A.1个 B.2个 C.0个 D.3个
?
5. 抛物线y=-3x2+2x-1与坐标轴的交点个数为( )
A.0个 B.1个 C.2个 D.3个
?
6. 如图,是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
A.x>3 B.x<-1 C.-1
?
7. 如图,已知直线y=kx+b(k>0)与抛物线y=x2交于A、B两点(A、B两点分别位于第二和第一象限),且A、B两点的纵坐标分别是1和9,则不等式x2-kx-b>0的解集为( )
A.-1
?
8. 二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象如图,ax2+bx+c=m有实数根的条件是( )
A.m≥-2 B.m≥5 C.m≥0 D.m>4
?
9. 如图,已知二次函数y1=23x2-43x的图象与正比例函数y2=23x的图象交于点A(3,?2),与x轴交于点B(2,?0),若y1
10. 小明利用二次函数的图象估计方程x2-2x-2=0的近似解,如表是小明探究过程中的一些计算数据.根据表中数据可知,方程x2-2x-2=0必有一个实数根在( )
x
1.5
2
2.5
3
3.5
x2-2x-2
-2.75
-2
-0.75
1
3.25
A.1.5和2之间 B.2和2.5之间 C.2.5和3之间 D.3和3.5之间
二、 填空题 (本题共计 7 小题 ,每题 3 分 ,共计21分 , ) ?
11. 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,?4),B(1,?1),则关于x的不等式ax2>bx+c的解集为________.
?
12. 抛物线y=x2-4x+c与x轴交于A、B两点,己知点A的坐标为(1,?0),则线段AB的长度为________.
?
13. 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次不等式-x2+2x+m<0的解集为________.
?
14. 已知二次函数y=-x2-2x+m的部分图象如图所示,则关于x的一元二次方程-x2-2x+m=0的解为________.
15. 抛物线y=ax2+b+c的部分图象如图所示,则当y<0时,x的取值范围是________. ?
16. 已知二次函数y=-x2+4x+m的部分图象如图,则关于x的一元二次方程-x2+4x+m=0的解是________.
17. 如图,在平面直角坐标系xOy中,直线y1=kx+m(k≠0)与抛物线y2=ax2+bx+c(a≠0)交于点A(0,?4),B(3,?1),当?y1≤y2时,x的取值范围是________.
三、 解答题 (本题共计 7 小题 ,共计69分 , )
?18 利用二次函数的图象求一元二次方程-2x2+4x+1=0的近似根.
?
19 已知二次函数y=-x2+2bx的图象经过原点及x轴上正半轴另一点A,设此二次函数图象的顶点为B.
(1)若△OAB是等腰直角三角形,求b的值;
(2)利用二次函数y=-x2+2bx的图象,试求不等式-x2+2bx+3>0的解集.
?
20 已知二次函数y=x2-4x-5,画出这个二次函数的图象,根据图象回答下列问题:
(1)方程x2-4x-5=0的解是什么?
(2)x取什么值时,函数值大于0?x取什么值时,函数值小于0?
?
21 如图,抛物线y=-12x2+bx+c 与轴交于点A,B,与y轴交于点C,直线y=-12x+2 经过点 A,C.
(1)求抛物线的解析式.
(2)点P为直线AC上方抛物线上一动点上.
①连结PO,交AC于点E,求?PEEO??的最大值.
②过点P作PF⊥AC垂足为点F,连结PC,是否存在点P,使△PFC中的一个角等于∠CAB的2倍?
若存在,请直接写出点P的坐标;若不存在,请说明理由.
?
22. 如图,二次函数y=x2-2x-3的图象与两坐标轴分别交于A,B,C三点,一次函数的图象与抛物线交于B,C两点.
(1)求点A,B,C的坐标;
(2)当两函数的函数值都随着x的增大而增大,求x的取值范围;
(3)当自变量x满足什么范围时,一次函数值大于二次函数值.
?
23 我们可以用如下方法解不等式(x-1)(x+1)>0.
第一步:画出函数y=(x-1)(x+1)的图象;
第二步:找出图象与x轴的交点坐标,即交点坐标为(1,?0),(-1,?0);
第三步:根据图象可知,在x<-1或x>1时,y的值大于0.因此可得不等式(x-1)(x+1)>0的解集为x<-1或x>1.
请你仿照上述方法,求不等式x2-4<0的解集.
?
24 在平面直角坐标系中,抛物线y=x2+bx+c经过A(-1,0)、B(1,0)、C三点, 且C点为抛物线与y轴的交点.
(1)求抛物线的表达式;
(2)连接BC,过点A作AP//BC交抛物线于点P,求以点A、P、B、C为顶点的四边形的面积;
(3)在(2)的条件下,在x轴上方的抛物线上是“ 否存在一点M,过M作MG⊥x轴于点G,使以A,M,G三点为顶点的三角形与△PCA相似? 若存在,求出点M的坐标;若不存在,请说明理由.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
【解答】
解:当y=0时,x2-1=0,
∵ Δ=02-4×1×(-1)=4>0,
∴ 方程x2-1=0有两个不相等的实数根,
即抛物线y=x2-1与x轴有两个交点.
故选B.
2.
【答案】
D
【解答】
解:
∵ 二次函数过点(1,?2),
∴ k-6+7=2,解得k=1,
∴ 抛物线解析式为y=x2-6x+7,
令y=可得x2-6x+7=0,
由题意可知x1和x2是该方程的两根,
∴ x1x2=7,
故选D.
3.
【答案】
D
【解答】
解:观察图象可知:抛物线y1与直线y2的交点横坐标是-2,1,
故当x<-2或x>1时,y1>y2.
故选:D.
4.
【答案】
B
【解答】
解:当与x轴相交时,函数值为0.即x2+3x-4=0,
△=b2-4ac=32-4×1×(-4)=25>0,
∴ 有2个不相等的实数根,
∴ 抛物线y=x2+3x-4与x轴有2个交点,
故选:B.
5.
【答案】
B
【解答】
解:∵ △=22-4×(-3)×(-1)=-8<0,
∴ 抛物线与x轴没有交点,
而抛物线y=-3x2+2x-1与y轴的交点为(0,?-1),
∴ 抛物线y=-3x2+2x-1与坐标轴的交点个数为1.
故选B.
6.
【答案】
D
【解答】
抛物线与x轴的另外一个交点的坐标为:(-1,?0),
从图象看,不等式ax2+bx+c<0的解集是:x>3或x<-1,
7.
【答案】
B
【解答】
解:由x2-kx-b>0得x2>kx+b,
∵ A、B两点的纵坐标分别是1和9,
∴ 点A的横坐标为-1,点B的横坐标为3,
当x<-1或x>3时,抛物线图象在直线图象上方,
故不等式x2-kx-b>0的解集为x<-1或x>3.
故选B.
8.
【答案】
A
【解答】
解:一元二次方程ax2+bx+c=m有实数根,
可以理解为y=ax2+bx+c和y=m有交点,
可见,m≥-2,
故选:A.
9.
【答案】
D
【解答】
解:如图所示:若y1
10.
【答案】
C
【解答】
解:根据表格得,当2.5
故选C.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
11.
【答案】
x>1或x<-2
【解答】
解:∵ 抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,?4),B(1,?1),
∴ 关于x的不等式ax2>bx+c的解集为x>1或x<-2,
故答案为:x>1或x<-2.
12.
【答案】
2
【解答】
解:∵ 抛物线y=x2-4x+c=(x-2)2-4+c,
∴ 抛物线的对称轴为直线x=2,
∵ 点A的坐标为(1,?0),
∴ 点B的坐标为(3,?0),
∴ 线段AB=3-1=2,
故答案为2.
13.
【答案】
x<-1或x>3
【解答】
解:由图可知,对称轴为直线x=1,
所以,二次函数图象与x轴的另一个交点坐标为(-1,?0),
所以,-x2+2x+m<0的解集为x<-1或x>3.
故答案为:x<-1或x>3.
14.
【答案】
x1=-3,x2=1
【解答】
解:由图象可得,
二次函数y=-x2-2x+m与x轴的一个交点为(-3,0),且对称轴为x=-1,
所以与x轴的另一个交点为(1,0),
所以关于x的一元二次方程-x2-2x+m=0的解为
二次函数y=-x2-2x+m与x轴的交点的横坐标,
即x1=-3,x2=1.
故答案为:x1=-3,x2=1.
15.
【答案】
x<-1或x>3
【解答】
解:∵ 抛物线与x轴的一个交点坐标是(-1,?0),对称轴是直线x=1,
∴ 抛物线与x轴另一交点的坐标是(3,?0),
∴ 当y<0时,x<-1或x>3.
故答案为:x<-1或x>3.
16.
【答案】
x1=-1,x2=5
【解答】
解:根据图示知,
二次函数y=-x2+4x+m的对称轴为x=2,与x轴的一个交点为(5,?0),
根据抛物线的对称性知,抛物线与x轴的另一个交点横坐标与点(5,?0)关于对称轴对称,即x=-1,
则另一交点坐标为(-1,?0)
则当x=-1或x=5时,函数值y=0,
即-x2+4x+m=0,
故关于x的一元二次方程-x2+4x+m=0的解为
x1=-1,x2=5.
故答案为:x1=-1,x2=5.
17.
【答案】
0≤x≤3
【解答】
∵ 两函数图象交于点A(0,?4),B(3,?1),
∴ 当?y1≤y2时,x的取值范围是0≤x≤3.
18.
【答案】
4
【解答】
解:①由y=ax2+bx+c与x轴的交点坐标为(-2,?0)得:
a×(-2)2+b×(-2?)+c=0,
即4a-2b+c=0,
所以①正确;
②由图象开口向下知a<0,
由y=ax2+bx+c与x轴的另一个交点
坐标为(x1,?0?),且1
即ba<1,
由a<0,两边都乘以a得:b>a,
∵ a<0,对称轴x=-b2a<0,
∴ b<0,
∴ a
结合a<0得2a+c>0,
所以结论③正确,
④由4a-2b+c=0得2a-b=-c2,
而0
∴ -1<2a-b<0,
∴ 2a-b+1>0,所以结论④正确.
故答案为:4.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
19.
【答案】
解:如图,
图象与x轴的交点坐标是(-0.2,?0)(2.2,?0),
一元二次方程-2x2+4x+1=0的近似根x1≈-0.2,x2≈2.2.
【解答】
解:如图,
图象与x轴的交点坐标是(-0.2,?0)(2.2,?0),
一元二次方程-2x2+4x+1=0的近似根x1≈-0.2,x2≈2.2.
20.
【答案】
解:(1)∵ △OAB是等腰直角三角形,
∴ 设B点横坐标为:a,则OA=2a,
故B点纵坐标为;(a,?a),
则a=-a2+2ba,-2b2×(-1)=a,则a=b,
故整理得:a2-a=0,
解得:a1=0(不合题意舍去),a2=1,
故b=1;
(2)由(1)得:y=-x2+2x,
则y=-x2+2x+3是y=-x2+2x向上平移3个单位得到的,
故y=0时,0=-x2+2x+3
解得:x1=-1,x2=3,
如图所示:不等式-x2+2bx+3>0的解集为:-1
解:(1)∵ △OAB是等腰直角三角形,
∴ 设B点横坐标为:a,则OA=2a,
故B点纵坐标为;(a,?a),
则a=-a2+2ba,-2b2×(-1)=a,则a=b,
故整理得:a2-a=0,
解得:a1=0(不合题意舍去),a2=1,
故b=1;
(2)由(1)得:y=-x2+2x,
则y=-x2+2x+3是y=-x2+2x向上平移3个单位得到的,
故y=0时,0=-x2+2x+3
解得:x1=-1,x2=3,
如图所示:不等式-x2+2bx+3>0的解集为:-1
【答案】
解:给出x的部分值,求出相应的y值,
列成如下表格:
按照表格中的数据在平面直角坐标系内,作出5个点:
A(-1,?0)、C(0,?5)、D(2,?-9)、E(4,?-5)、B(5,?0),
用平滑的曲线将5个点连接起来,即得函数的图象.
(1)由图象可知:x1=-1,x2=5.
(2)由图象可知:当x<-1或x>5时,y>0;
当-1
解:给出x的部分值,求出相应的y值,
列成如下表格:
按照表格中的数据在平面直角坐标系内,作出5个点:
A(-1,?0)、C(0,?5)、D(2,?-9)、E(4,?-5)、B(5,?0),
用平滑的曲线将5个点连接起来,即得函数的图象.
(1)由图象可知:x1=-1,x2=5.
(2)由图象可知:当x<-1或x>5时,y>0;
当-1
【答案】
解:(1)对于y=-12x+2,
当x=0时,y=2,
当y=0时,x=4,
∴ A(4,0),C(0,2).
∵ 抛物线y=-12x2+bx+c经过点A(4,0),C(0,2),
∴ -8+4b+c=0,c=2,
解得b=-32,c=2.
故抛物线的解析式为y=-12x2+32x+2.
(2)①如图(1),过点P作PN⊥x轴于点N,交直线AC于点M,
则PN//y轴,
∴ ∠PME=∠OCE,
又∵ ∠PEM=∠OEC,
∴ △PEM?△OEC,
∴ PEEO=PMOC.
∵ C(0,2),
∴ OC=2.
设点P的坐标为(t,-12t2+32t+2),
则点Mt,-12t+2,
∴ PM=-12t2+32t+2--12t+2=-12t2+2t,
∴ PEEO=-14t2+t=-14(t-2)2+1.
∵ -14<0,0
②存在,
易得∠PFC≠2∠CAB,分以下两种情况.
当∠PCF=2∠CAB时,如图(2),在y轴上取点D,使点C于点D关于x轴对称,连结AD,
则∠CAB=∠DAB,点D的坐标为(0,-2).
∴ ∠PCF=∠CAD,
∴ PC//AD,
设直线AD的解析式为y=kx+d,
则d=-2,4k+d=0,
解得k=12,d=-2.
故直线AD的解析式为y=12x-2,直线PC的解析式为y=12x+2.
令-12x2+32x+2=12x+2,
整理,得x2-2x=0,
解得x1=0(不合题意,舍去),x2=2.
当x=2时,y=-12×22+32×2+2=3,
故点P的坐标为(2,3).
当∠CPF=2∠CAB时,如图(3),过点C作CH⊥AD于点H,过点A作AG⊥CP,交CP的延长线于点G,
易得∠ACP=∠ACH,
从而可得AG=AH,CG=CH.
由勾股定理可得AC=AD=25,
由三角形面积公式可得12AD?CH=12CD?OA,
即12×25CH=12×4×4,
解得CH=85.
由勾股定理得AH=65,
∴ CG=85,AG=65.
过点G作GQ⊥x轴于点Q,作GR⊥y轴于点R,
设点G的坐标为(m,n),则GH=m,GQ=n.
在Rt△GAQ和Rt△GCR中,
由勾股定理得(4-m)2+n2=652,m2+(n-2)2=852,
解得m1=8825,n1=6625,m2=85,n2=-65,(不合题意,舍去)
设直线CG的解析式为y=k1x+e,
将C(0,2) G8825,6625分别代入,
得e=2,8825k1+e=6625,
解得k1=211,e=2,
故直线CG的解析式为y=211x+2.
令-12x2+32x+2=211x+2,
整理,得11x2-29x=0,
解得x1=2911,x2=0,(不合题意,舍去).
在y=211x+2,
当x=2911时,y=211×2911+2=300121,
故点P的坐标为2911,300121.
综上,点P的坐标为(2,3)或2911,300121.
【解答】
解:(1)对于y=-12x+2,
当x=0时,y=2,
当y=0时,x=4,
∴ A(4,0),C(0,2).
∵ 抛物线y=-12x2+bx+c经过点A(4,0),C(0,2),
∴ -8+4b+c=0,c=2,
解得b=-32,c=2.
故抛物线的解析式为y=-12x2+32x+2.
(2)①如图(1),过点P作PN⊥x轴于点N,交直线AC于点M,
则PN//y轴,
∴ ∠PME=∠OCE,
又∵ ∠PEM=∠OEC,
∴ △PEM?△OEC,
∴ PEEO=PMOC.
∵ C(0,2),
∴ OC=2.
设点P的坐标为(t,-12t2+32t+2),
则点Mt,-12t+2,
∴ PM=-12t2+32t+2--12t+2=-12t2+2t,
∴ PEEO=-14t2+t=-14(t-2)2+1.
∵ -14<0,0
②存在,
易得∠PFC≠2∠CAB,分以下两种情况.
当∠PCF=2∠CAB时,如图(2),在y轴上取点D,使点C于点D关于x轴对称,连结AD,
则∠CAB=∠DAB,点D的坐标为(0,-2).
∴ ∠PCF=∠CAD,
∴ PC//AD,
设直线AD的解析式为y=kx+d,
则d=-2,4k+d=0,
解得k=12,d=-2.
故直线AD的解析式为y=12x-2,直线PC的解析式为y=12x+2.
令-12x2+32x+2=12x+2,
整理,得x2-2x=0,
解得x1=0(不合题意,舍去),x2=2.
当x=2时,y=-12×22+32×2+2=3,
故点P的坐标为(2,3).
当∠CPF=2∠CAB时,如图(3),过点C作CH⊥AD于点H,过点A作AG⊥CP,交CP的延长线于点G,
易得∠ACP=∠ACH,
从而可得AG=AH,CG=CH.
由勾股定理可得AC=AD=25,
由三角形面积公式可得12AD?CH=12CD?OA,
即12×25CH=12×4×4,
解得CH=85.
由勾股定理得AH=65,
∴ CG=85,AG=65.
过点G作GQ⊥x轴于点Q,作GR⊥y轴于点R,
设点G的坐标为(m,n),则GH=m,GQ=n.
在Rt△GAQ和Rt△GCR中,
由勾股定理得(4-m)2+n2=652,m2+(n-2)2=852,
解得m1=8825,n1=6625,m2=85,n2=-65,(不合题意,舍去)
设直线CG的解析式为y=k1x+e,
将C(0,2)?G8825,6625分别代入,
得e=2,8825k1+e=6625,
解得k1=211,e=2,
故直线CG的解析式为y=211x+2.
令-12x2+32x+2=211x+2,
整理,得11x2-29x=0,
解得x1=2911,x2=0,(不合题意,舍去).
在y=211x+2,
当x=2911时,y=211×2911+2=300121,
故点P的坐标为2911,300121.
综上,点P的坐标为(2,3)或2911,300121.
23.
【答案】
解:(1)∵ 令x=0,则y=-3,
∴ C(0,?-3).
∵ 令y=0,则x2-2x-3=0,解得x=-1或x=3,
∴ A(-1,?0),B(3,?0).
(2)∵ 由(1)知,A(-1,?0),B(3,?0),
∴ 抛物线的对称轴为直线x=3-12=1,
∴ 当x>1时,两函数的函数值都随着x的增大而增大;
(3)∵ 由函数图象可知,当0
解:(1)∵ 令x=0,则y=-3,
∴ C(0,?-3).
∵ 令y=0,则x2-2x-3=0,解得x=-1或x=3,
∴ A(-1,?0),B(3,?0).
(2)∵ 由(1)知,A(-1,?0),B(3,?0),
∴ 抛物线的对称轴为直线x=3-12=1,
∴ 当x>1时,两函数的函数值都随着x的增大而增大;
(3)∵ 由函数图象可知,当0
【答案】
解:如图,不等式x2-4<0的解集是-2
解:如图,不等式x2-4<0的解集是-2
【答案】
解:(1)∵ 抛物线y=x2+bx+c经过点A(-1,0)、B(1,0),
∴ 1-b+c=01+b+c=0,解得b=0c=-1,
∴ 抛物线额的表达式为y=x2-1;
(2)将x=0代入y=x2-1,得y=-1,
∴ C(0,-1),OC=1
∵ OA=OB=OC=1
∴ ∠BAC=∠ACO=∠BCO=∠ABC=45?
∵ AP//BC
∴ ∠PAB=∠ABC=45?,
如解图①,过点P作PE⊥x轴于点E,则△APE为等腰直角三角形,
令OE=a,则PE=AE=a+1,
∴ P(a,a+1),
∵ 点P在抛物线y=x2-1上,
∴ a+1=a2-1,
解得a1=2,a2=-1(不合题意,舍去),
∴ PE=3,
∴ S四边形ACBP=SΔABC+S△ABP=12AB?OC+12AB?PE=12×2×1+12×2×3=4;
(3)存在,
如解图②,
∵ ∠PAB=∠BAC=45?,
∴ PA⊥AC,
∴ ∠MGA=∠PAC=90?,
在Rt△AOC中,OA=OC=1,
∴ AC=OA2+OC2=2,
在Rt△PAE中,AE=PE=3,
∴ AP=AE2+PE2=32,
设M点横坐标为m,则M(m,m2-1),
∵ 点M在x轴上方抛物线上,
∴ m2-1>0,
∴ m<-1或m>1,
①当M在y轴左侧时,则m<-1.
(i)当△AMG?△PCA时,有AGPA=MGCA,
∵ AG=-m-1,MG=m2-1,
∴ -m-132=m2-12,
解得m1=-1(舍去),m2=23(舍去);
(ii)当△MAG?△PCA时,有AGCA=MGPA,
即-m-12=m2-132,
解得m1=-1(舍去),m2=-2,
∴ M(-2,3);
②点M在y轴右侧时,则m>1,
(i)当△AMG?△PCA时,有AGPA=MGCA,
∵ AG=m+1,MG=m2-1,
∴ m+132=m2-12,解得m1=-1?(舍去),m2=43,
∴ M(43,79);
(ii)当△MAG?△PCA时,有AGCA=MGPA,
即m+12=m2-132,解得m1=-1(舍去),m2=4,
∴ M(4,15),
综上所述,存在点M,使以A,M,G三点为顶点的三角形与△PCA相似,点M的坐标为(-2,3)或(43,79)或(4,15).
【解答】
解:(1)∵ 抛物线y=x2+bx+c经过点A(-1,0)、B(1,0),
∴ 1-b+c=01+b+c=0,解得b=0c=-1,
∴ 抛物线额的表达式为y=x2-1;
(2)将x=0代入y=x2-1,得y=-1,
∴ C(0,-1),OC=1
∵ OA=OB=OC=1
∴ ∠BAC=∠ACO=∠BCO=∠ABC=45?
∵ AP//BC
∴ ∠PAB=∠ABC=45?,
如解图①,过点P作PE⊥x轴于点E,则△APE为等腰直角三角形,
令OE=a,则PE=AE=a+1,
∴ P(a,a+1),
∵ 点P在抛物线y=x2-1上,
∴ a+1=a2-1,
解得a1=2,a2=-1(不合题意,舍去),
∴ PE=3,
∴ S四边形ACBP=SΔABC+S△ABP=12AB?OC+12AB?PE=12×2×1+12×2×3=4;
(3)存在,
如解图②,
∵ ∠PAB=∠BAC=45?,
∴ PA⊥AC,
∴ ∠MGA=∠PAC=90?,
在Rt△AOC中,OA=OC=1,
∴ AC=OA2+OC2=2,
在Rt△PAE中,AE=PE=3,
∴ AP=AE2+PE2=32,
设M点横坐标为m,则M(m,m2-1),
∵ 点M在x轴上方抛物线上,
∴ m2-1>0,
∴ m<-1或m>1,
①当M在y轴左侧时,则m<-1.
(i)当△AMG?△PCA时,有AGPA=MGCA,
∵ AG=-m-1,MG=m2-1,
∴ -m-132=m2-12,
解得m1=-1(舍去),m2=23(舍去);
(ii)当△MAG?△PCA时,有AGCA=MGPA,
即-m-12=m2-132,
解得m1=-1(舍去),m2=-2,
∴ M(-2,3);
②点M在y轴右侧时,则m>1,
(i)当△AMG?△PCA时,有AGPA=MGCA,
∵ AG=m+1,MG=m2-1,
∴ m+132=m2-12,解得m1=-1?(舍去),m2=43,
∴ M(43,79);
(ii)当△MAG?△PCA时,有AGCA=MGPA,
即m+12=m2-132,解得m1=-1(舍去),m2=4,
∴ M(4,15),
综上所述,存在点M,使以A,M,G三点为顶点的三角形与△PCA相似,点M的坐标为(-2,3)或(43,79)或(4,15).
