用二分法求方程的近似解
图片预览








文档简介
(共45张PPT)
引例
方程2010x2-2012x+1=0 有实根吗?
方程lnx+2x=6有实根吗?如何求?
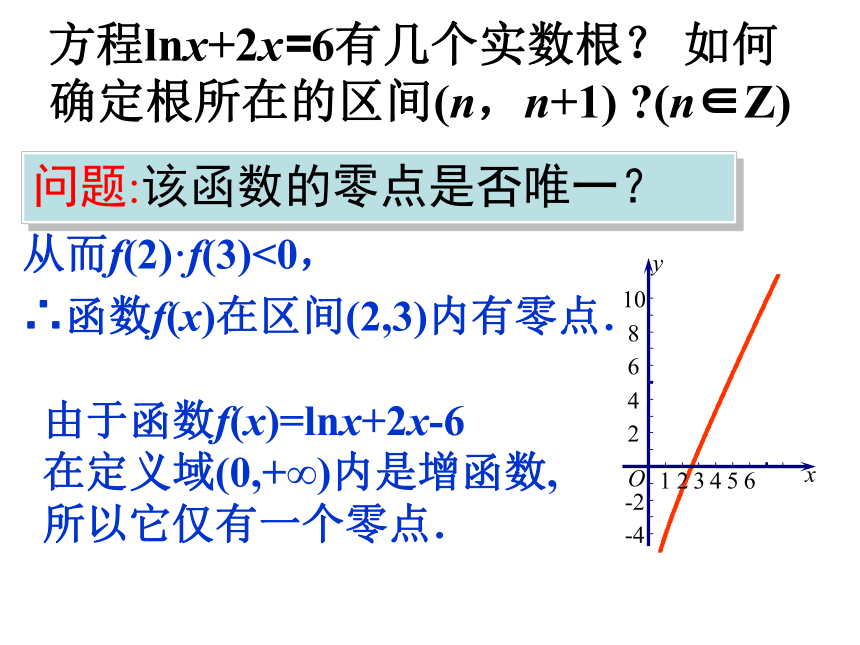
由表可知f(2)<0,f(3)>0,
从而f(2)·f(3)<0,
∴函数f(x)在区间(2,3)内有零点.
用计算器列出x、f(x)的对应值表
方程lnx+2x=6有几个实数根? 如何确定根所在的区间(n,n+1) (n∈Z)
问题:你能说明判断的依据吗?
x 1 2 3 4 5 6 7 8 9
f(x)
-4
-1.3
1.1
3.4
5.6
7.8
10.0
12.1
14.2
解:令 f(x)= lnx+2x-6,可求函数零点的个数
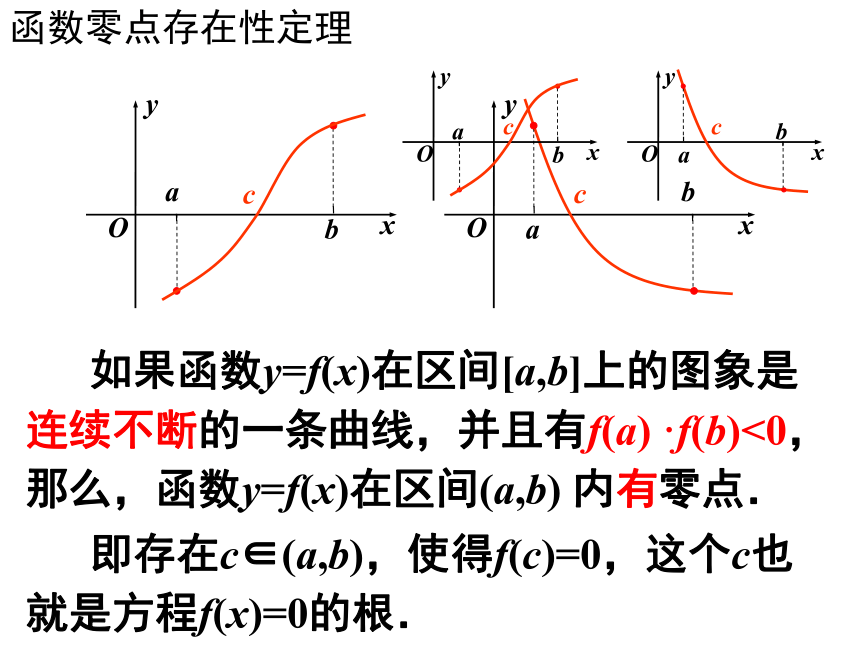
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a) ·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点.
即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
函数零点存在性定理
x
y
O
b
a
c
x
y
O
a
b
c
x
y
O
b
a
c
x
y
O
a
b
c
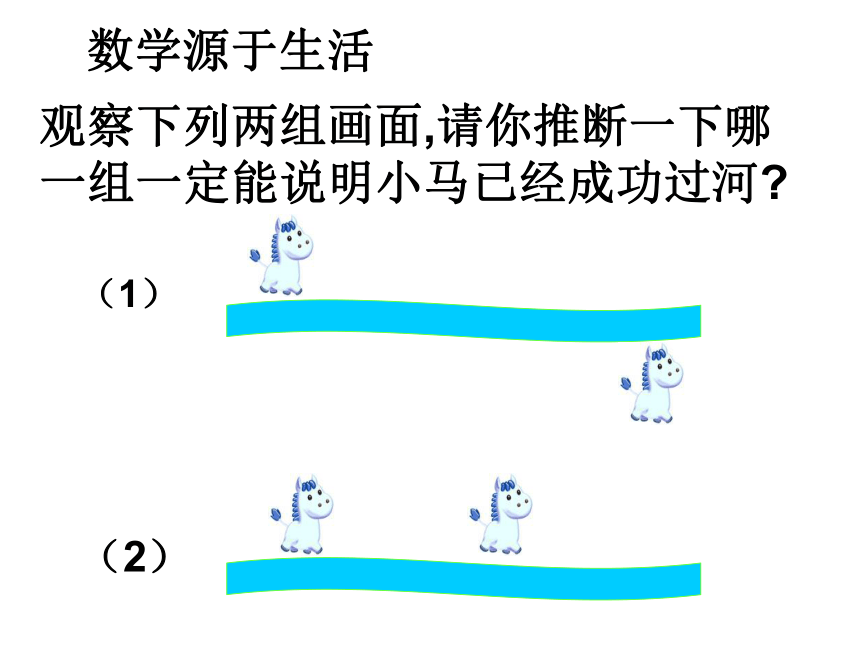
(1)
(2)
观察下列两组画面,请你推断一下哪一组一定能说明小马已经成功过河
数学源于生活
由表可知f(2)<0,f(3)>0,
从而f(2)·f(3)<0,
∴函数f(x)在区间(2,3)内有零点.
由于函数f(x)=lnx+2x-6
在定义域(0,+∞)内是增函数,
所以它仅有一个零点.
方程lnx+2x=6有几个实数根? 如何确定根所在的区间(n,n+1) (n∈Z)
问题:该函数的零点是否唯一?
10
8
6
4
2
-2
-4
5
1
2
3
4
6
x
y
O
2.你有何方法求该零点的近似值
1.你能找出函数零点落在下列哪个区间吗?
方程lnx+2x=6实数根 个数
函数f(x)=lnx+2x-6的零点个数
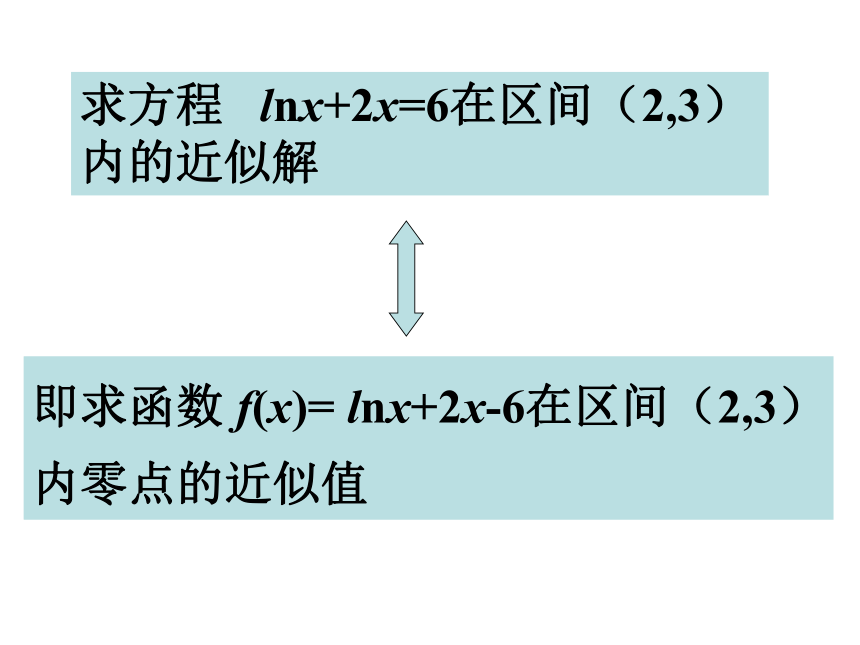
求方程 lnx+2x=6在区间(2,3)内的近似解
即求函数 f(x)= lnx+2x-6在区间(2,3)
内零点的近似值
请你谈谈你的设计方案
是否有更为高效经济的算法?
3.1.2 用二分法求方程的近似解
区 间(a,b) 中点值c f(c)近似值 |a-b|
2.5
2.75
2.625
2.5625
2.53125
2.546875
2.5390625
2.53515625
-0.084
0.512
0.215
0.066
-0.009
0.029
0.010
0.001
(精确度0.01)
(2,3)
二分法求方程 lnx+2x=6的近似解
(2.5,3)
(2.5,2.75)
(2.5,2.625)
(2.5,2.5625)
(2.53125,2.5625)
(2.53125,2.546875)
(2.53125,2.5390625)
1
0.5
0.25
0.125
0.0625
0.03125
0.015625
0.0078125
方程 lnx+2x=6的近似解可取2.53125
对于区间[a,b]上连续不断且f(a) ·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点 零点,进而得到零点近似值的方法叫做二分法(bisection).
逐步逼近
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
3.计算f(c);
2.求区间(a,b)的中点c;
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a)· f(c)<0,则令b= c(此时零点x0∈(a, c) );
(3)若f(c)· f(b)<0,则令a= c(此时零点x0∈( c, b) ).
4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2~4.
一般步骤:
编写程序
二分法的实质就是将函数零点所在的区间不断地一分为二,使新得到的区间不断变小,两个端点逐步逼近零点.
思考:下列函数中能用二分法求零点的是____.
(1) (4)
(2)
(1)
(3)
(4)
例 借助计算器或计算机用二分法求方程2x+3x=7的近似解(精确度0.1).
构造函数
列表作图
判断零点及其个数
确定零点所属区间
用二分法求近似解
解题流程:
2 4 6 8
-4 -2
-2
-4
-6
24 22 20 18 16 14 12 10 8 6 4 2
y
x
0
解:原方程即2x+3x-7=0,令f(x)= 2x+3x-7,用计算器作出函数f(x)= 2x + 3x -7 的对应值表和图象如下:
x 0 1 2 3 4 5 6
f(x) -6 -2 3 10 21 40 75
观察图象及上表可知f(1)·f(2)<0,又因为f(x)在R内是增函数,所以 f(x)= 2x+3x-7有唯一的零点
x0∈(1,2).
取区间(1,2)的中点x1=1.5, 用计算器算得
f(1.5) ≈ 0.33,因为f(1)·f(1.5)<0所以x0 ∈(1,1.5)
再取区间(1,1.5)的中点x2=1.25 ,用计算器算得f(1.25) ≈ -0.87,因为 ,所以
x0∈
同理可得,
x0∈(1.375,1.5),x0∈(1.375,1.4375),
由于 |1.375-1.4375|=0.0625< 0.1,
所以,原方程的近似解可取为1.4375.
(1.25,1.5).
f(1.25)·f(1.5)<0
确定初始区间
求中点,算其函数值
缩小区间
算长度,比精度
下结论
返
回
用二分法求函数零点近似值的流程图
周而复始怎么办 精确度上来判断.
定区间,找中点, 中值计算两边看.
同号去,异号算, 零点落在异号间.
二分法秘诀
生活中也常常会用到二分法思想:
在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路有一处发生了故障。这是一条10km长的线路,如何迅速查出故障所在
如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次电线杆子,10km长,大约有200多根电线杆子呢。
想一想,维修线路的工人师傅至少经过几次查找可使故障范围缩小到50~100m左右?
如图,维修工人首先从中点C.查用随身带的话机向两个端点测试时,发现AC段正常,断定故障在BC段,再到BC段中点D,这次发现BD段正常,可见故障在CD段,再到CD中点E来查.每查一次,可以把待查的线路长度缩减一半,如此查下去,至多7次,就能把故障点锁定在一两根电线杆附近.
闸门A
指挥部B
C
D
E待查区D
通过本节课的学习与思考,你有哪些收获?
函数
方程
转化思想
逼近思想
数学
源于生活
数学
用于生活
二分法
数形结合
1.寻找解所在的区间
2.不断二分解所在的区间
3.根据精确度得出近似解
用二分法求方程的近似解
算法思想
作业布置
课本P92 A组3,4,5中任选2题
课本P93 B组第2题
阅读与思考
《中外历史上的方程求解》
《借助信息技术求方程的近似解》
网络资源下载 www.
让你我打开
尘封了一个冬季的心灵
让你我打开
自己的向往
和春天一起上路
在清新的泥土里
种下至亲至爱的词语
让青春的魔力在春天里弹跳
来吧,伸手拥抱
你、我和春天有个约会
读万卷书,行万里路!
行万里路胜读万卷书!
------春游有感
我买了一坛绍兴黄酒,价格在100元~300元之间,请你猜测它的价格(误差不超过10元)并思考按什么样的规律猜才能提高猜测的效率
(每次猜后会如实给出
多了还是少了的提示)
猜价格游戏
问题一:给出多了还是少了的提示有什么作用?
问题二:误差不超过10元,怎么理解?
问题三:误差不超过1元能在8次之内猜中吗?
问题四: 你应该如何猜才能最快猜出这坛黄酒的价格?
思考:
数学就像你的朋友,只要你眼里充满爱,就会发现她就在你身边,不离不弃相伴一生。
-------国藩语录
返回
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a) ·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点.
即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
函数零点存在性定理
x
y
O
b
a
c
x
y
O
a
b
c
x
y
O
b
a
c
x
y
O
a
b
c
思考题
从上海到美国旧金山的海底电缆有15个接点,现在某接点发生故障,需及时修理,为了尽快断定故障发生点,一般至少需要检查几个接点?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
回顾反思(理解数学)
引例
方程2010x2-2012x+1=0 有实根吗?
方程lnx+2x=6有实根吗?如何求?
由表可知f(2)<0,f(3)>0,
从而f(2)·f(3)<0,
∴函数f(x)在区间(2,3)内有零点.
用计算器列出x、f(x)的对应值表
方程lnx+2x=6有几个实数根? 如何确定根所在的区间(n,n+1) (n∈Z)
问题:你能说明判断的依据吗?
x 1 2 3 4 5 6 7 8 9
f(x)
-4
-1.3
1.1
3.4
5.6
7.8
10.0
12.1
14.2
解:令 f(x)= lnx+2x-6,可求函数零点的个数
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a) ·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点.
即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
函数零点存在性定理
x
y
O
b
a
c
x
y
O
a
b
c
x
y
O
b
a
c
x
y
O
a
b
c
(1)
(2)
观察下列两组画面,请你推断一下哪一组一定能说明小马已经成功过河
数学源于生活
由表可知f(2)<0,f(3)>0,
从而f(2)·f(3)<0,
∴函数f(x)在区间(2,3)内有零点.
由于函数f(x)=lnx+2x-6
在定义域(0,+∞)内是增函数,
所以它仅有一个零点.
方程lnx+2x=6有几个实数根? 如何确定根所在的区间(n,n+1) (n∈Z)
问题:该函数的零点是否唯一?
10
8
6
4
2
-2
-4
5
1
2
3
4
6
x
y
O
2.你有何方法求该零点的近似值
1.你能找出函数零点落在下列哪个区间吗?
方程lnx+2x=6实数根 个数
函数f(x)=lnx+2x-6的零点个数
求方程 lnx+2x=6在区间(2,3)内的近似解
即求函数 f(x)= lnx+2x-6在区间(2,3)
内零点的近似值
请你谈谈你的设计方案
是否有更为高效经济的算法?
3.1.2 用二分法求方程的近似解
区 间(a,b) 中点值c f(c)近似值 |a-b|
2.5
2.75
2.625
2.5625
2.53125
2.546875
2.5390625
2.53515625
-0.084
0.512
0.215
0.066
-0.009
0.029
0.010
0.001
(精确度0.01)
(2,3)
二分法求方程 lnx+2x=6的近似解
(2.5,3)
(2.5,2.75)
(2.5,2.625)
(2.5,2.5625)
(2.53125,2.5625)
(2.53125,2.546875)
(2.53125,2.5390625)
1
0.5
0.25
0.125
0.0625
0.03125
0.015625
0.0078125
方程 lnx+2x=6的近似解可取2.53125
对于区间[a,b]上连续不断且f(a) ·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点 零点,进而得到零点近似值的方法叫做二分法(bisection).
逐步逼近
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
3.计算f(c);
2.求区间(a,b)的中点c;
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a)· f(c)<0,则令b= c(此时零点x0∈(a, c) );
(3)若f(c)· f(b)<0,则令a= c(此时零点x0∈( c, b) ).
4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2~4.
一般步骤:
编写程序
二分法的实质就是将函数零点所在的区间不断地一分为二,使新得到的区间不断变小,两个端点逐步逼近零点.
思考:下列函数中能用二分法求零点的是____.
(1) (4)
(2)
(1)
(3)
(4)
例 借助计算器或计算机用二分法求方程2x+3x=7的近似解(精确度0.1).
构造函数
列表作图
判断零点及其个数
确定零点所属区间
用二分法求近似解
解题流程:
2 4 6 8
-4 -2
-2
-4
-6
24 22 20 18 16 14 12 10 8 6 4 2
y
x
0
解:原方程即2x+3x-7=0,令f(x)= 2x+3x-7,用计算器作出函数f(x)= 2x + 3x -7 的对应值表和图象如下:
x 0 1 2 3 4 5 6
f(x) -6 -2 3 10 21 40 75
观察图象及上表可知f(1)·f(2)<0,又因为f(x)在R内是增函数,所以 f(x)= 2x+3x-7有唯一的零点
x0∈(1,2).
取区间(1,2)的中点x1=1.5, 用计算器算得
f(1.5) ≈ 0.33,因为f(1)·f(1.5)<0所以x0 ∈(1,1.5)
再取区间(1,1.5)的中点x2=1.25 ,用计算器算得f(1.25) ≈ -0.87,因为 ,所以
x0∈
同理可得,
x0∈(1.375,1.5),x0∈(1.375,1.4375),
由于 |1.375-1.4375|=0.0625< 0.1,
所以,原方程的近似解可取为1.4375.
(1.25,1.5).
f(1.25)·f(1.5)<0
确定初始区间
求中点,算其函数值
缩小区间
算长度,比精度
下结论
返
回
用二分法求函数零点近似值的流程图
周而复始怎么办 精确度上来判断.
定区间,找中点, 中值计算两边看.
同号去,异号算, 零点落在异号间.
二分法秘诀
生活中也常常会用到二分法思想:
在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路有一处发生了故障。这是一条10km长的线路,如何迅速查出故障所在
如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次电线杆子,10km长,大约有200多根电线杆子呢。
想一想,维修线路的工人师傅至少经过几次查找可使故障范围缩小到50~100m左右?
如图,维修工人首先从中点C.查用随身带的话机向两个端点测试时,发现AC段正常,断定故障在BC段,再到BC段中点D,这次发现BD段正常,可见故障在CD段,再到CD中点E来查.每查一次,可以把待查的线路长度缩减一半,如此查下去,至多7次,就能把故障点锁定在一两根电线杆附近.
闸门A
指挥部B
C
D
E待查区D
通过本节课的学习与思考,你有哪些收获?
函数
方程
转化思想
逼近思想
数学
源于生活
数学
用于生活
二分法
数形结合
1.寻找解所在的区间
2.不断二分解所在的区间
3.根据精确度得出近似解
用二分法求方程的近似解
算法思想
作业布置
课本P92 A组3,4,5中任选2题
课本P93 B组第2题
阅读与思考
《中外历史上的方程求解》
《借助信息技术求方程的近似解》
网络资源下载 www.
让你我打开
尘封了一个冬季的心灵
让你我打开
自己的向往
和春天一起上路
在清新的泥土里
种下至亲至爱的词语
让青春的魔力在春天里弹跳
来吧,伸手拥抱
你、我和春天有个约会
读万卷书,行万里路!
行万里路胜读万卷书!
------春游有感
我买了一坛绍兴黄酒,价格在100元~300元之间,请你猜测它的价格(误差不超过10元)并思考按什么样的规律猜才能提高猜测的效率
(每次猜后会如实给出
多了还是少了的提示)
猜价格游戏
问题一:给出多了还是少了的提示有什么作用?
问题二:误差不超过10元,怎么理解?
问题三:误差不超过1元能在8次之内猜中吗?
问题四: 你应该如何猜才能最快猜出这坛黄酒的价格?
思考:
数学就像你的朋友,只要你眼里充满爱,就会发现她就在你身边,不离不弃相伴一生。
-------国藩语录
返回
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a) ·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点.
即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
函数零点存在性定理
x
y
O
b
a
c
x
y
O
a
b
c
x
y
O
b
a
c
x
y
O
a
b
c
思考题
从上海到美国旧金山的海底电缆有15个接点,现在某接点发生故障,需及时修理,为了尽快断定故障发生点,一般至少需要检查几个接点?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
回顾反思(理解数学)
