北师大版七年级上期末复习第三章测试卷(含解析)
文档属性
| 名称 | 北师大版七年级上期末复习第三章测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 17:34:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版七年级上期末复习第三章测试卷
时间120分钟 满分120分
一.选择题(每小题3分,共30分)
1.(2019秋?玉田县期末)下列各式中,符合代数式书写规则的是( )
A. B. C. D.2y÷z
2.(2020春?香坊区期末)买一个足球需m元,买一个篮球需n元,则买4个足球和7个篮球共需( )元.
A.11mn B.28mn C.4m+7n D.7m+4n
3.(2020春?泰山区期末)如图,是一个运算程序的示意图,若开始输入x的值为625,则第2020次输出的结果为( )
A.1 B.5 C.25 D.625
4.(2020春?哈尔滨期末)下列式子x,﹣3,﹣x2+2,﹣mn中,单项式有( )个.
A.1 B.2 C.3 D.4
5.(2019秋?岳阳楼区校级期末)关于整式的概念,下列说法正确的是( )
A.的系数是
B.32x3y的次数是6
C.3是单项式
D.﹣x2y+xy﹣7是5次三项式
6.(2020春?哈尔滨期末)下列各组中的两项,属于同类项的是( )
A.a2与a B.﹣3ab与2ab C.a2b与ab2 D.a与b
7.(2019秋?凌源市期末)下列运算中,正确的是( )
A.2a+3b=5ab B.2a2+3a2=5a2
C.3a2﹣2a2=1 D.2a2b﹣2ab2=0
8.(2020秋?沧州期中)下列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z B.19a2b﹣9ba2=10a2b
C.﹣2 (x+y)﹣z=﹣2x+2y﹣z D.3a3+2a2=5a5
9.(2020秋?温县期中)已知a+b=3,c﹣d=2,则(a+c)﹣(﹣b+d)的值是( )
A.5 B.﹣5 C.1 D.﹣1
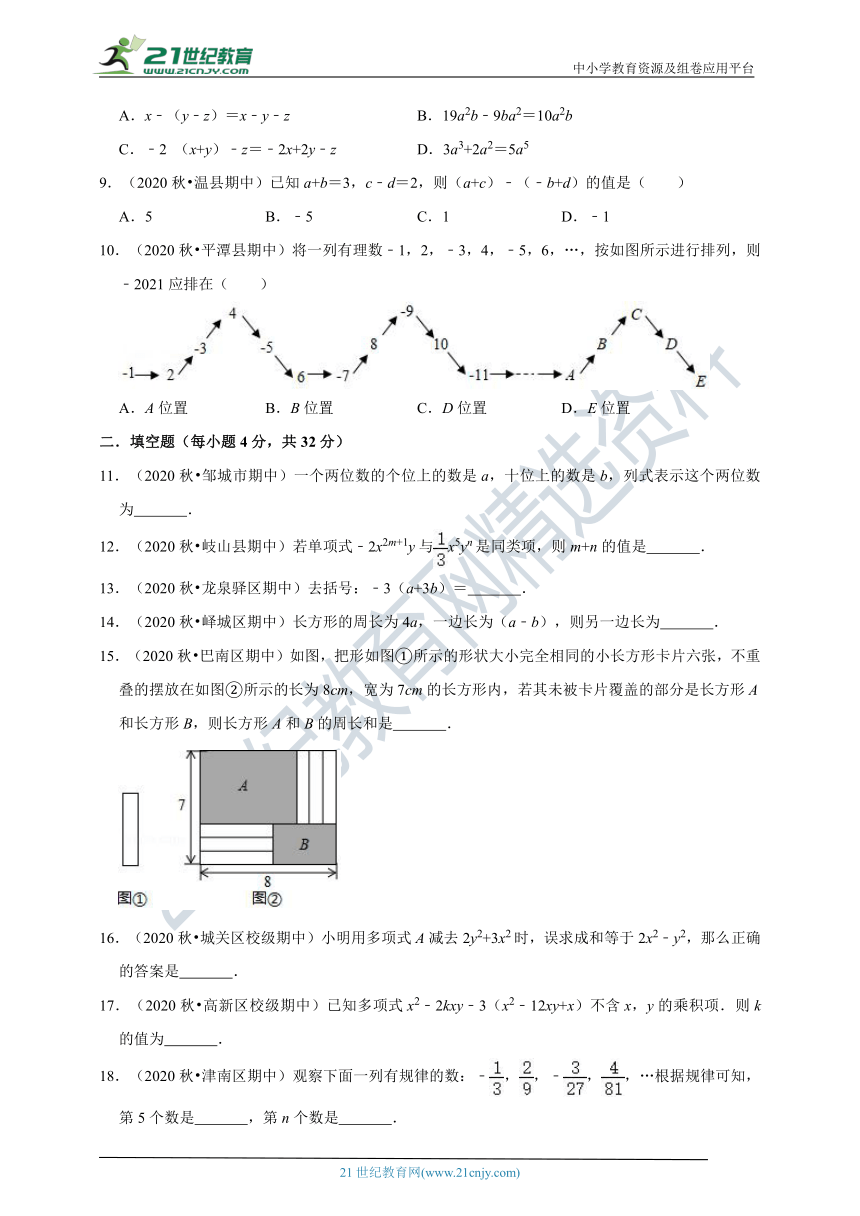
10.(2020秋?平潭县期中)将一列有理数﹣1,2,﹣3,4,﹣5,6,…,按如图所示进行排列,则﹣2021应排在( )
A.A位置 B.B位置 C.D位置 D.E位置
二.填空题(每小题4分,共32分)
11.(2020秋?邹城市期中)一个两位数的个位上的数是a,十位上的数是b,列式表示这个两位数为 .
12.(2020秋?岐山县期中)若单项式﹣2x2m+1y与x5yn是同类项,则m+n的值是 .
13.(2020秋?龙泉驿区期中)去括号:﹣3(a+3b)= .
14.(2020秋?峄城区期中)长方形的周长为4a,一边长为(a﹣b),则另一边长为 .
15.(2020秋?巴南区期中)如图,把形如图①所示的形状大小完全相同的小长方形卡片六张,不重叠的摆放在如图②所示的长为8cm,宽为7cm的长方形内,若其未被卡片覆盖的部分是长方形A和长方形B,则长方形A和B的周长和是 .
16.(2020秋?城关区校级期中)小明用多项式A减去2y2+3x2时,误求成和等于2x2﹣y2,那么正确的答案是 .
17.(2020秋?高新区校级期中)已知多项式x2﹣2kxy﹣3(x2﹣12xy+x)不含x,y的乘积项.则k的值为 .
18.(2020秋?津南区期中)观察下面一列有规律的数:﹣,,﹣,,…根据规律可知,第5个数是 ,第n个数是 .
三.解答题(共58分)
19.(10分)(2020秋?东港市期中)如图在某居民区规划修建一个广场(图中阴影部分).
(1)用含m,n的代数式表示该广场的周长C;
(2)用含m,n的代数式表示该广场的面积S;
(3)当m=4,n=6时,求该广场的周长和面积.
20.(10分)(2020秋?庆阳期中)已知多项式A=ax4+4x2﹣,B=3xb﹣5x,若A,B两个多项式的次数相同,且最高次数项的系数互为相反数.
(1)求a,b的值;
(2)求b2﹣3b+4b﹣5的值.
21.(10分)(2020秋?邵阳县期中)化简:
(1)(2x2﹣+3x)﹣4(x﹣x2+);
(2)3x2﹣[7x﹣(﹣3+4x)﹣2x2].
22.(10分)(2020秋?解放区校级期中)先化简,再求值:
(1)(4a2﹣3a)﹣(1﹣4a+4a2),其中a=﹣2.
(2)2(x2y+xy)﹣3(x2y﹣xy)﹣4x2y,其中x=1,y=﹣1.
23.(8分)(2020秋?城关区校级期中)张老师让同学们计算,当x=2019,y=2020时,求代数式2(x﹣2y)﹣6(x﹣y﹣1)的值.
由于小明抄题时粗心大意,把“x=2019,y=2020”写成了“x=19,y=20”,但他求出来的结果却是正确的,你知道为什么吗?请解释是怎么一回事,并计算最后的值.
24.(10分)(2020秋?邹城市期中)观察下面三行数:
①2,﹣4,8,﹣16,32,﹣64…;
②﹣1,﹣7,5,﹣19,29,﹣67…;
③2,﹣1,5,﹣7,17,﹣31….
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)取每行数的第8个数,计算这三个数的和.
北师大版七年级上期末复习第三章测试卷
参考答案与试题解析
一.选择题
1.(2019秋?玉田县期末)下列各式中,符合代数式书写规则的是( )
A. B. C. D.2y÷z
【分析】根据代数式的书写要求判断各项.
【解答】解:A、符合代数式书写规则.
B、不符合代数式书写规则,应该为;
C、不符合代数式书写规则,应该为﹣;
D、不符合代数式书写规则,应改为;
故选:A.
2.(2020春?香坊区期末)买一个足球需m元,买一个篮球需n元,则买4个足球和7个篮球共需( )元.
A.11mn B.28mn C.4m+7n D.7m+4n
【分析】根据单价×数量=金额表示出足球与篮球各自的费用,再将两个费用求和便可得总费用.
【解答】解:根据题意得,买4个足球和7个篮球的总费用为(4m+7n)元,
故选:C.
3.(2020春?泰山区期末)如图,是一个运算程序的示意图,若开始输入x的值为625,则第2020次输出的结果为( )
A.1 B.5 C.25 D.625
【分析】依次求出每次输出的结果,根据结果得出规律,即可得出答案.
【解答】解:当x=625时,x=125,
当x=125时,x=25,
当x=25时,x=5,
当x=5时,x=1,
当x=1时,x+4=5,
当x=5时,x=1,
…
依此类推,以5,1循环,
(2020﹣2)÷2=1009,能够整除,
所以输出的结果是1,
故选:A.
4.(2020春?哈尔滨期末)下列式子x,﹣3,﹣x2+2,﹣mn中,单项式有( )个.
A.1 B.2 C.3 D.4
【分析】根据单项式的定义逐个判断即可.
【解答】解:单项式有x,﹣3,﹣mn,共3个,
故选:C.
5.(2019秋?岳阳楼区校级期末)关于整式的概念,下列说法正确的是( )
A.的系数是
B.32x3y的次数是6
C.3是单项式
D.﹣x2y+xy﹣7是5次三项式
【分析】注意单项式的系数为其数字因数,次数是所有字母的次数的和,单个的数或字母也是单项式,多项式的次数是多项式中最高次项的次数,项数为所含单项式的个数.
【解答】解:A、﹣的系数为﹣,错误;
B、32x3y的次数是4,错误;
C、3是单项式,正确;
D、多项式﹣x2y+xy﹣7是三次三项式,错误;
故选:C.
6.(2020春?哈尔滨期末)下列各组中的两项,属于同类项的是( )
A.a2与a B.﹣3ab与2ab C.a2b与ab2 D.a与b
【分析】根据同类项的定义对四个选项进行逐一分析即可.
【解答】解:A、a2与a中所含字母的指数不同,不是同类项,故此选项不符合题意;
B、﹣3ab与2ab中所含字母相同,相同字母的指数也相同,是同类项,故此选项符合题意;
C、a2b与ab2中所含字母相同,相同字母的指数不相同,不是同类项,故此选项不符合题意;
D、a与b中所含字母不同,不是同类项,故此选项不符合题意.
故选:B.
7.(2019秋?凌源市期末)下列运算中,正确的是( )
A.2a+3b=5ab B.2a2+3a2=5a2
C.3a2﹣2a2=1 D.2a2b﹣2ab2=0
【分析】根据合并同类项法则逐一判断即可.
【解答】解:A.2a与3b不是同类项,所以不能合并,故本选项不合题意;
B.2a2+3a2=5a2,故本选项符合题意;
C.3a2﹣2a2=a2,故本选项不合题意;
D.2a2b与﹣2ab2不是同类项,所以不能合并,故本选项不合题意.
故选:B.
8.(2020秋?沧州期中)下列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z B.19a2b﹣9ba2=10a2b
C.﹣2 (x+y)﹣z=﹣2x+2y﹣z D.3a3+2a2=5a5
【分析】根据去括号法则和合并同类项的法则解答.
【解答】解:A、原式=x﹣y+z,故本选项不符合题意.
B、原式=x﹣y﹣z,故本选项符合题意.
C、原式=﹣2x﹣2y﹣z,故本选项不符合题意.
D、3a3与2a2不是同类项,不能合并,故本选项不符合题意.
故选:B.
9.(2020秋?温县期中)已知a+b=3,c﹣d=2,则(a+c)﹣(﹣b+d)的值是( )
A.5 B.﹣5 C.1 D.﹣1
【分析】根据整式的运算法则即可求出答案.
【解答】解:原式=a+c+b﹣d
=a+b+c﹣d,
当a+c=3,c﹣d=2时,
∴原式=3+2
=5,
故选:A.
10.(2020秋?平潭县期中)将一列有理数﹣1,2,﹣3,4,﹣5,6,…,按如图所示进行排列,则﹣2021应排在( )
A.A位置 B.B位置 C.D位置 D.E位置
【分析】根据图中的数字,可以发现数字的变化特点,从而可以求得﹣2021应排在哪个位置,本题得以解决.
【解答】解:由图可知,
每个凸起对应5个数字,这些数字的奇数都是负数,偶数都是正数,
∵(2021﹣1)÷5=2020÷5=404,
∴﹣2021应排在E位置,
故选:D.
二.填空题
11.(2020秋?邹城市期中)一个两位数的个位上的数是a,十位上的数是b,列式表示这个两位数为 10b+a .
【分析】个位数字a,十位数字b的两位数可以表示为:10b+a.
【解答】个位数字a,十位数字b的两位数是:10×b+1×a
=10b+a,故答案为:10b﹣a.
12.(2020秋?岐山县期中)若单项式﹣2x2m+1y与x5yn是同类项,则m+n的值是 3 .
【分析】根据同类项的概念即可求出m与n的值,然后代入原式即可求出答案.
【解答】解:由题意可知:2m+1=5,n=1,
∴m=2,n=1,
∴m+n=2+1=3,
故答案为:3.
13.(2020秋?龙泉驿区期中)去括号:﹣3(a+3b)= ﹣3a﹣9b .
【分析】根据去括号法则解答即可.
【解答】解:﹣3(a+3b)
=﹣3a﹣9b.
故答案为:﹣3a﹣9b.
14.(2020秋?峄城区期中)长方形的周长为4a,一边长为(a﹣b),则另一边长为 2a+2b .
【分析】根据题意列出算式即可求出答案.
【解答】解:另一边长为:4a﹣2(a﹣b)
=4a﹣2a+2b
=2a+2b,
故答案为:2a+2b.
15.(2020秋?巴南区期中)如图,把形如图①所示的形状大小完全相同的小长方形卡片六张,不重叠的摆放在如图②所示的长为8cm,宽为7cm的长方形内,若其未被卡片覆盖的部分是长方形A和长方形B,则长方形A和B的周长和是 32 .
【分析】设小长方形的长与宽分别为a、b,根据题意列出算式即可求出答案.
【解答】解:设小长方形的长与宽分别为a、b,
∴长方形A的长与宽为:a、8﹣3b,
长方形B的长与宽为:8﹣a,3b,
所以长方形A与B的周长之和为:2[a+(8﹣3b)+(8﹣a)+3b]
=2×16
=32,
故答案为:32.
16.(2020秋?城关区校级期中)小明用多项式A减去2y2+3x2时,误求成和等于2x2﹣y2,那么正确的答案是 ﹣4x2﹣5y2 .
【分析】根据题意列出关系式,去括号合并即可得到结果.
【解答】解:根据题意得:(2x2﹣y2)﹣2(2y2+3x2)
=2x2﹣y2﹣4y2﹣6x2
=﹣4x2﹣5y2.
故答案为:﹣4x2﹣5y2.
17.(2020秋?高新区校级期中)已知多项式x2﹣2kxy﹣3(x2﹣12xy+x)不含x,y的乘积项.则k的值为 18 .
【分析】直接去括号合并同类项,再利用xy的系数为零得出答案.
【解答】解:x2﹣2kxy﹣3(x2﹣12xy+x)
=x2﹣2kxy﹣3x2+36xy﹣3x
=﹣x2+(﹣2k+36)xy﹣3x,
∵多项式x2﹣2kxy﹣3(x2﹣12xy+x)不含x,y的乘积项,
∴﹣2k+36=0,
解得:k=18.
故答案为:18.
18.(2020秋?津南区期中)观察下面一列有规律的数:﹣,,﹣,,…根据规律可知,第5个数是 ﹣ ,第n个数是 .
【分析】根据题目中数字的特点,可以写出第5个数和第n个数,本题得以解决.
【解答】解:∵一列有规律的数:﹣,,﹣,,…,
∴这列数可以写为:﹣,,,,…,
∴第5个数是:=﹣,第n个数是,
故答案为:﹣,.
三.解答题
19.(2020秋?东港市期中)如图在某居民区规划修建一个广场(图中阴影部分).
(1)用含m,n的代数式表示该广场的周长C;
(2)用含m,n的代数式表示该广场的面积S;
(3)当m=4,n=6时,求该广场的周长和面积.
【分析】(1)观察图形,根据周长的定义计算即可;
(2)广场的面积S等于长为2n,宽为2m的长方形的面积减去长为m,宽为(2n﹣n﹣0.5n)的长方形的面积;
(3)将m=4,n=6分别代入(1)和(2)中所得的代数式,计算即可.
【解答】解:(1)由图形可得:
C=2m×2+2n×2+2m=6m+4n;
(2)S=2n×2m﹣(2n﹣n﹣0.5n)m
=4mn﹣0.5mn
=3.5mn;
(3)当m=4,n=6时,
C=6m+4n
=6×4+4×6
=24+24
=48;
S=3.5mn
=3.5×4×6
=84.
20.(2020秋?庆阳期中)已知多项式A=ax4+4x2﹣,B=3xb﹣5x,若A,B两个多项式的次数相同,且最高次数项的系数互为相反数.
(1)求a,b的值;
(2)求b2﹣3b+4b﹣5的值.
【分析】(1)根据多项式的定义以及合并同类项法则即可求出a与b的值;
(2)把b的值代入所求式子计算即可.
【解答】解:(1)∵多项式A=ax4+4x2﹣,B=3xb﹣5x,若A,B两个多项式的次数相同,且最高次数项的系数互为相反数,
∴;
(2)b2﹣3b+4b﹣5
=,
把b=4代入得:
=
=8+4﹣5
=7.
21.(2020秋?邵阳县期中)化简:
(1)(2x2﹣+3x)﹣4(x﹣x2+);
(2)3x2﹣[7x﹣(﹣3+4x)﹣2x2].
【分析】(1)直接去括号,再合并同类项得出答案;
(2)直接去括号,再合并同类项得出答案.
【解答】解:(1)(2x2﹣+3x)﹣4(x﹣x2+)
=2x2﹣+3x﹣4x+4x2﹣2
=6x2﹣x﹣;
(2)3x2﹣[7x﹣(﹣3+4x)﹣2x2]
=3x2﹣7x+(﹣3+4x)+2x2
=3x2﹣7x﹣3+4x+2x2
=5x2﹣3x﹣3.
22.(2020秋?解放区校级期中)先化简,再求值:
(1)(4a2﹣3a)﹣(1﹣4a+4a2),其中a=﹣2.
(2)2(x2y+xy)﹣3(x2y﹣xy)﹣4x2y,其中x=1,y=﹣1.
【分析】去括号,合并同类项后,再代入求值即可.
【解答】解:(1)(4a2﹣3a)﹣(1﹣4a+4a2)
=4a2﹣3a﹣1+4a﹣4a2
=a﹣1,
∵a=﹣2,
∴原式=﹣2﹣1=﹣3.
(2)2(x2y+xy)﹣3(x2y﹣xy)﹣4x2y
=2x2y+2xy﹣3x2y+3xy﹣4x2y
=﹣5x2y+5xy,
∵x=1,y=﹣1,∴原式=﹣5×1×(﹣1)+5×1×(﹣1)=5﹣5=0.
23.(2020秋?城关区校级期中)张老师让同学们计算,当x=2019,y=2020时,求代数式2(x﹣2y)﹣6(x﹣y﹣1)的值.
由于小明抄题时粗心大意,把“x=2019,y=2020”写成了“x=19,y=20”,但他求出来的结果却是正确的,你知道为什么吗?请解释是怎么一回事,并计算最后的值.
【分析】利用去括号、合并同类项化简后,根据结果进行判断即可.
【解答】解:2(x﹣2y)﹣6(x﹣y﹣1)
=2x﹣4y﹣2x+4y+6
=6,
结果是常数6,与x、y的值无关,
因此小明抄错了x、y不影响结果,
故结果为6.
24.(2020秋?邹城市期中)观察下面三行数:
①2,﹣4,8,﹣16,32,﹣64…;
②﹣1,﹣7,5,﹣19,29,﹣67…;
③2,﹣1,5,﹣7,17,﹣31….
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)取每行数的第8个数,计算这三个数的和.
【分析】(1)观察可得从第一个数开始,后面一个数是前面一个数乘以(﹣2)得到的;
(2)比较相应位置上的数即可得出答案;
(3)根据(2)中所得的规律分别计算出这三个数,再计算这三个数的和即可.
【解答】解:(1)第①行数的规律是:从第一个数开始,后面一个数是前面一个数乘以(﹣2)得到的,即2,2×(﹣2),﹣4×(﹣2),8×(﹣2),﹣16×(﹣2),32×(﹣2),…;
(2)第②行数每个位置上的数是第①行数相应位置上的数减3得到的,即:
2﹣3=﹣1,﹣4﹣3=﹣7,8﹣3=5,﹣16﹣3=﹣19,32﹣3=29,﹣64﹣3=﹣67…;
第③行数每个位置上的数是第①行数相应位置上的数除以2再加上1得到的,即:
2÷2+1=2,﹣4÷2+1=﹣1,8÷2+1=5,﹣16÷2+1=﹣7,32÷2+1=17,﹣64÷2+1=﹣31,…;
(3)第①行数的第8个数为:﹣64×(﹣2)×(﹣2)=﹣256;
第②行数第8个数为:﹣256﹣3=﹣259;
第③行数的第8个数为:﹣256÷2+1=﹣127,
∴这三个数的和为:﹣256﹣259﹣127=﹣642.
_21?????????è?????(www.21cnjy.com)_
北师大版七年级上期末复习第三章测试卷
时间120分钟 满分120分
一.选择题(每小题3分,共30分)
1.(2019秋?玉田县期末)下列各式中,符合代数式书写规则的是( )
A. B. C. D.2y÷z
2.(2020春?香坊区期末)买一个足球需m元,买一个篮球需n元,则买4个足球和7个篮球共需( )元.
A.11mn B.28mn C.4m+7n D.7m+4n
3.(2020春?泰山区期末)如图,是一个运算程序的示意图,若开始输入x的值为625,则第2020次输出的结果为( )
A.1 B.5 C.25 D.625
4.(2020春?哈尔滨期末)下列式子x,﹣3,﹣x2+2,﹣mn中,单项式有( )个.
A.1 B.2 C.3 D.4
5.(2019秋?岳阳楼区校级期末)关于整式的概念,下列说法正确的是( )
A.的系数是
B.32x3y的次数是6
C.3是单项式
D.﹣x2y+xy﹣7是5次三项式
6.(2020春?哈尔滨期末)下列各组中的两项,属于同类项的是( )
A.a2与a B.﹣3ab与2ab C.a2b与ab2 D.a与b
7.(2019秋?凌源市期末)下列运算中,正确的是( )
A.2a+3b=5ab B.2a2+3a2=5a2
C.3a2﹣2a2=1 D.2a2b﹣2ab2=0
8.(2020秋?沧州期中)下列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z B.19a2b﹣9ba2=10a2b
C.﹣2 (x+y)﹣z=﹣2x+2y﹣z D.3a3+2a2=5a5
9.(2020秋?温县期中)已知a+b=3,c﹣d=2,则(a+c)﹣(﹣b+d)的值是( )
A.5 B.﹣5 C.1 D.﹣1
10.(2020秋?平潭县期中)将一列有理数﹣1,2,﹣3,4,﹣5,6,…,按如图所示进行排列,则﹣2021应排在( )
A.A位置 B.B位置 C.D位置 D.E位置
二.填空题(每小题4分,共32分)
11.(2020秋?邹城市期中)一个两位数的个位上的数是a,十位上的数是b,列式表示这个两位数为 .
12.(2020秋?岐山县期中)若单项式﹣2x2m+1y与x5yn是同类项,则m+n的值是 .
13.(2020秋?龙泉驿区期中)去括号:﹣3(a+3b)= .
14.(2020秋?峄城区期中)长方形的周长为4a,一边长为(a﹣b),则另一边长为 .
15.(2020秋?巴南区期中)如图,把形如图①所示的形状大小完全相同的小长方形卡片六张,不重叠的摆放在如图②所示的长为8cm,宽为7cm的长方形内,若其未被卡片覆盖的部分是长方形A和长方形B,则长方形A和B的周长和是 .
16.(2020秋?城关区校级期中)小明用多项式A减去2y2+3x2时,误求成和等于2x2﹣y2,那么正确的答案是 .
17.(2020秋?高新区校级期中)已知多项式x2﹣2kxy﹣3(x2﹣12xy+x)不含x,y的乘积项.则k的值为 .
18.(2020秋?津南区期中)观察下面一列有规律的数:﹣,,﹣,,…根据规律可知,第5个数是 ,第n个数是 .
三.解答题(共58分)
19.(10分)(2020秋?东港市期中)如图在某居民区规划修建一个广场(图中阴影部分).
(1)用含m,n的代数式表示该广场的周长C;
(2)用含m,n的代数式表示该广场的面积S;
(3)当m=4,n=6时,求该广场的周长和面积.
20.(10分)(2020秋?庆阳期中)已知多项式A=ax4+4x2﹣,B=3xb﹣5x,若A,B两个多项式的次数相同,且最高次数项的系数互为相反数.
(1)求a,b的值;
(2)求b2﹣3b+4b﹣5的值.
21.(10分)(2020秋?邵阳县期中)化简:
(1)(2x2﹣+3x)﹣4(x﹣x2+);
(2)3x2﹣[7x﹣(﹣3+4x)﹣2x2].
22.(10分)(2020秋?解放区校级期中)先化简,再求值:
(1)(4a2﹣3a)﹣(1﹣4a+4a2),其中a=﹣2.
(2)2(x2y+xy)﹣3(x2y﹣xy)﹣4x2y,其中x=1,y=﹣1.
23.(8分)(2020秋?城关区校级期中)张老师让同学们计算,当x=2019,y=2020时,求代数式2(x﹣2y)﹣6(x﹣y﹣1)的值.
由于小明抄题时粗心大意,把“x=2019,y=2020”写成了“x=19,y=20”,但他求出来的结果却是正确的,你知道为什么吗?请解释是怎么一回事,并计算最后的值.
24.(10分)(2020秋?邹城市期中)观察下面三行数:
①2,﹣4,8,﹣16,32,﹣64…;
②﹣1,﹣7,5,﹣19,29,﹣67…;
③2,﹣1,5,﹣7,17,﹣31….
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)取每行数的第8个数,计算这三个数的和.
北师大版七年级上期末复习第三章测试卷
参考答案与试题解析
一.选择题
1.(2019秋?玉田县期末)下列各式中,符合代数式书写规则的是( )
A. B. C. D.2y÷z
【分析】根据代数式的书写要求判断各项.
【解答】解:A、符合代数式书写规则.
B、不符合代数式书写规则,应该为;
C、不符合代数式书写规则,应该为﹣;
D、不符合代数式书写规则,应改为;
故选:A.
2.(2020春?香坊区期末)买一个足球需m元,买一个篮球需n元,则买4个足球和7个篮球共需( )元.
A.11mn B.28mn C.4m+7n D.7m+4n
【分析】根据单价×数量=金额表示出足球与篮球各自的费用,再将两个费用求和便可得总费用.
【解答】解:根据题意得,买4个足球和7个篮球的总费用为(4m+7n)元,
故选:C.
3.(2020春?泰山区期末)如图,是一个运算程序的示意图,若开始输入x的值为625,则第2020次输出的结果为( )
A.1 B.5 C.25 D.625
【分析】依次求出每次输出的结果,根据结果得出规律,即可得出答案.
【解答】解:当x=625时,x=125,
当x=125时,x=25,
当x=25时,x=5,
当x=5时,x=1,
当x=1时,x+4=5,
当x=5时,x=1,
…
依此类推,以5,1循环,
(2020﹣2)÷2=1009,能够整除,
所以输出的结果是1,
故选:A.
4.(2020春?哈尔滨期末)下列式子x,﹣3,﹣x2+2,﹣mn中,单项式有( )个.
A.1 B.2 C.3 D.4
【分析】根据单项式的定义逐个判断即可.
【解答】解:单项式有x,﹣3,﹣mn,共3个,
故选:C.
5.(2019秋?岳阳楼区校级期末)关于整式的概念,下列说法正确的是( )
A.的系数是
B.32x3y的次数是6
C.3是单项式
D.﹣x2y+xy﹣7是5次三项式
【分析】注意单项式的系数为其数字因数,次数是所有字母的次数的和,单个的数或字母也是单项式,多项式的次数是多项式中最高次项的次数,项数为所含单项式的个数.
【解答】解:A、﹣的系数为﹣,错误;
B、32x3y的次数是4,错误;
C、3是单项式,正确;
D、多项式﹣x2y+xy﹣7是三次三项式,错误;
故选:C.
6.(2020春?哈尔滨期末)下列各组中的两项,属于同类项的是( )
A.a2与a B.﹣3ab与2ab C.a2b与ab2 D.a与b
【分析】根据同类项的定义对四个选项进行逐一分析即可.
【解答】解:A、a2与a中所含字母的指数不同,不是同类项,故此选项不符合题意;
B、﹣3ab与2ab中所含字母相同,相同字母的指数也相同,是同类项,故此选项符合题意;
C、a2b与ab2中所含字母相同,相同字母的指数不相同,不是同类项,故此选项不符合题意;
D、a与b中所含字母不同,不是同类项,故此选项不符合题意.
故选:B.
7.(2019秋?凌源市期末)下列运算中,正确的是( )
A.2a+3b=5ab B.2a2+3a2=5a2
C.3a2﹣2a2=1 D.2a2b﹣2ab2=0
【分析】根据合并同类项法则逐一判断即可.
【解答】解:A.2a与3b不是同类项,所以不能合并,故本选项不合题意;
B.2a2+3a2=5a2,故本选项符合题意;
C.3a2﹣2a2=a2,故本选项不合题意;
D.2a2b与﹣2ab2不是同类项,所以不能合并,故本选项不合题意.
故选:B.
8.(2020秋?沧州期中)下列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z B.19a2b﹣9ba2=10a2b
C.﹣2 (x+y)﹣z=﹣2x+2y﹣z D.3a3+2a2=5a5
【分析】根据去括号法则和合并同类项的法则解答.
【解答】解:A、原式=x﹣y+z,故本选项不符合题意.
B、原式=x﹣y﹣z,故本选项符合题意.
C、原式=﹣2x﹣2y﹣z,故本选项不符合题意.
D、3a3与2a2不是同类项,不能合并,故本选项不符合题意.
故选:B.
9.(2020秋?温县期中)已知a+b=3,c﹣d=2,则(a+c)﹣(﹣b+d)的值是( )
A.5 B.﹣5 C.1 D.﹣1
【分析】根据整式的运算法则即可求出答案.
【解答】解:原式=a+c+b﹣d
=a+b+c﹣d,
当a+c=3,c﹣d=2时,
∴原式=3+2
=5,
故选:A.
10.(2020秋?平潭县期中)将一列有理数﹣1,2,﹣3,4,﹣5,6,…,按如图所示进行排列,则﹣2021应排在( )
A.A位置 B.B位置 C.D位置 D.E位置
【分析】根据图中的数字,可以发现数字的变化特点,从而可以求得﹣2021应排在哪个位置,本题得以解决.
【解答】解:由图可知,
每个凸起对应5个数字,这些数字的奇数都是负数,偶数都是正数,
∵(2021﹣1)÷5=2020÷5=404,
∴﹣2021应排在E位置,
故选:D.
二.填空题
11.(2020秋?邹城市期中)一个两位数的个位上的数是a,十位上的数是b,列式表示这个两位数为 10b+a .
【分析】个位数字a,十位数字b的两位数可以表示为:10b+a.
【解答】个位数字a,十位数字b的两位数是:10×b+1×a
=10b+a,故答案为:10b﹣a.
12.(2020秋?岐山县期中)若单项式﹣2x2m+1y与x5yn是同类项,则m+n的值是 3 .
【分析】根据同类项的概念即可求出m与n的值,然后代入原式即可求出答案.
【解答】解:由题意可知:2m+1=5,n=1,
∴m=2,n=1,
∴m+n=2+1=3,
故答案为:3.
13.(2020秋?龙泉驿区期中)去括号:﹣3(a+3b)= ﹣3a﹣9b .
【分析】根据去括号法则解答即可.
【解答】解:﹣3(a+3b)
=﹣3a﹣9b.
故答案为:﹣3a﹣9b.
14.(2020秋?峄城区期中)长方形的周长为4a,一边长为(a﹣b),则另一边长为 2a+2b .
【分析】根据题意列出算式即可求出答案.
【解答】解:另一边长为:4a﹣2(a﹣b)
=4a﹣2a+2b
=2a+2b,
故答案为:2a+2b.
15.(2020秋?巴南区期中)如图,把形如图①所示的形状大小完全相同的小长方形卡片六张,不重叠的摆放在如图②所示的长为8cm,宽为7cm的长方形内,若其未被卡片覆盖的部分是长方形A和长方形B,则长方形A和B的周长和是 32 .
【分析】设小长方形的长与宽分别为a、b,根据题意列出算式即可求出答案.
【解答】解:设小长方形的长与宽分别为a、b,
∴长方形A的长与宽为:a、8﹣3b,
长方形B的长与宽为:8﹣a,3b,
所以长方形A与B的周长之和为:2[a+(8﹣3b)+(8﹣a)+3b]
=2×16
=32,
故答案为:32.
16.(2020秋?城关区校级期中)小明用多项式A减去2y2+3x2时,误求成和等于2x2﹣y2,那么正确的答案是 ﹣4x2﹣5y2 .
【分析】根据题意列出关系式,去括号合并即可得到结果.
【解答】解:根据题意得:(2x2﹣y2)﹣2(2y2+3x2)
=2x2﹣y2﹣4y2﹣6x2
=﹣4x2﹣5y2.
故答案为:﹣4x2﹣5y2.
17.(2020秋?高新区校级期中)已知多项式x2﹣2kxy﹣3(x2﹣12xy+x)不含x,y的乘积项.则k的值为 18 .
【分析】直接去括号合并同类项,再利用xy的系数为零得出答案.
【解答】解:x2﹣2kxy﹣3(x2﹣12xy+x)
=x2﹣2kxy﹣3x2+36xy﹣3x
=﹣x2+(﹣2k+36)xy﹣3x,
∵多项式x2﹣2kxy﹣3(x2﹣12xy+x)不含x,y的乘积项,
∴﹣2k+36=0,
解得:k=18.
故答案为:18.
18.(2020秋?津南区期中)观察下面一列有规律的数:﹣,,﹣,,…根据规律可知,第5个数是 ﹣ ,第n个数是 .
【分析】根据题目中数字的特点,可以写出第5个数和第n个数,本题得以解决.
【解答】解:∵一列有规律的数:﹣,,﹣,,…,
∴这列数可以写为:﹣,,,,…,
∴第5个数是:=﹣,第n个数是,
故答案为:﹣,.
三.解答题
19.(2020秋?东港市期中)如图在某居民区规划修建一个广场(图中阴影部分).
(1)用含m,n的代数式表示该广场的周长C;
(2)用含m,n的代数式表示该广场的面积S;
(3)当m=4,n=6时,求该广场的周长和面积.
【分析】(1)观察图形,根据周长的定义计算即可;
(2)广场的面积S等于长为2n,宽为2m的长方形的面积减去长为m,宽为(2n﹣n﹣0.5n)的长方形的面积;
(3)将m=4,n=6分别代入(1)和(2)中所得的代数式,计算即可.
【解答】解:(1)由图形可得:
C=2m×2+2n×2+2m=6m+4n;
(2)S=2n×2m﹣(2n﹣n﹣0.5n)m
=4mn﹣0.5mn
=3.5mn;
(3)当m=4,n=6时,
C=6m+4n
=6×4+4×6
=24+24
=48;
S=3.5mn
=3.5×4×6
=84.
20.(2020秋?庆阳期中)已知多项式A=ax4+4x2﹣,B=3xb﹣5x,若A,B两个多项式的次数相同,且最高次数项的系数互为相反数.
(1)求a,b的值;
(2)求b2﹣3b+4b﹣5的值.
【分析】(1)根据多项式的定义以及合并同类项法则即可求出a与b的值;
(2)把b的值代入所求式子计算即可.
【解答】解:(1)∵多项式A=ax4+4x2﹣,B=3xb﹣5x,若A,B两个多项式的次数相同,且最高次数项的系数互为相反数,
∴;
(2)b2﹣3b+4b﹣5
=,
把b=4代入得:
=
=8+4﹣5
=7.
21.(2020秋?邵阳县期中)化简:
(1)(2x2﹣+3x)﹣4(x﹣x2+);
(2)3x2﹣[7x﹣(﹣3+4x)﹣2x2].
【分析】(1)直接去括号,再合并同类项得出答案;
(2)直接去括号,再合并同类项得出答案.
【解答】解:(1)(2x2﹣+3x)﹣4(x﹣x2+)
=2x2﹣+3x﹣4x+4x2﹣2
=6x2﹣x﹣;
(2)3x2﹣[7x﹣(﹣3+4x)﹣2x2]
=3x2﹣7x+(﹣3+4x)+2x2
=3x2﹣7x﹣3+4x+2x2
=5x2﹣3x﹣3.
22.(2020秋?解放区校级期中)先化简,再求值:
(1)(4a2﹣3a)﹣(1﹣4a+4a2),其中a=﹣2.
(2)2(x2y+xy)﹣3(x2y﹣xy)﹣4x2y,其中x=1,y=﹣1.
【分析】去括号,合并同类项后,再代入求值即可.
【解答】解:(1)(4a2﹣3a)﹣(1﹣4a+4a2)
=4a2﹣3a﹣1+4a﹣4a2
=a﹣1,
∵a=﹣2,
∴原式=﹣2﹣1=﹣3.
(2)2(x2y+xy)﹣3(x2y﹣xy)﹣4x2y
=2x2y+2xy﹣3x2y+3xy﹣4x2y
=﹣5x2y+5xy,
∵x=1,y=﹣1,∴原式=﹣5×1×(﹣1)+5×1×(﹣1)=5﹣5=0.
23.(2020秋?城关区校级期中)张老师让同学们计算,当x=2019,y=2020时,求代数式2(x﹣2y)﹣6(x﹣y﹣1)的值.
由于小明抄题时粗心大意,把“x=2019,y=2020”写成了“x=19,y=20”,但他求出来的结果却是正确的,你知道为什么吗?请解释是怎么一回事,并计算最后的值.
【分析】利用去括号、合并同类项化简后,根据结果进行判断即可.
【解答】解:2(x﹣2y)﹣6(x﹣y﹣1)
=2x﹣4y﹣2x+4y+6
=6,
结果是常数6,与x、y的值无关,
因此小明抄错了x、y不影响结果,
故结果为6.
24.(2020秋?邹城市期中)观察下面三行数:
①2,﹣4,8,﹣16,32,﹣64…;
②﹣1,﹣7,5,﹣19,29,﹣67…;
③2,﹣1,5,﹣7,17,﹣31….
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)取每行数的第8个数,计算这三个数的和.
【分析】(1)观察可得从第一个数开始,后面一个数是前面一个数乘以(﹣2)得到的;
(2)比较相应位置上的数即可得出答案;
(3)根据(2)中所得的规律分别计算出这三个数,再计算这三个数的和即可.
【解答】解:(1)第①行数的规律是:从第一个数开始,后面一个数是前面一个数乘以(﹣2)得到的,即2,2×(﹣2),﹣4×(﹣2),8×(﹣2),﹣16×(﹣2),32×(﹣2),…;
(2)第②行数每个位置上的数是第①行数相应位置上的数减3得到的,即:
2﹣3=﹣1,﹣4﹣3=﹣7,8﹣3=5,﹣16﹣3=﹣19,32﹣3=29,﹣64﹣3=﹣67…;
第③行数每个位置上的数是第①行数相应位置上的数除以2再加上1得到的,即:
2÷2+1=2,﹣4÷2+1=﹣1,8÷2+1=5,﹣16÷2+1=﹣7,32÷2+1=17,﹣64÷2+1=﹣31,…;
(3)第①行数的第8个数为:﹣64×(﹣2)×(﹣2)=﹣256;
第②行数第8个数为:﹣256﹣3=﹣259;
第③行数的第8个数为:﹣256÷2+1=﹣127,
∴这三个数的和为:﹣256﹣259﹣127=﹣642.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
