北师大版数学七年级下册第1章1 同底数幂的乘法(共18张PPT)
文档属性
| 名称 | 北师大版数学七年级下册第1章1 同底数幂的乘法(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 401.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 21:07:34 | ||
图片预览






文档简介
同底数幂的乘法
学习目标
1.经历同底数幂的乘法运算性质的过程,能总结出同底数幂乘法的运算性质。
2.能利用同底数幂的乘法运算性质解决相关问题。
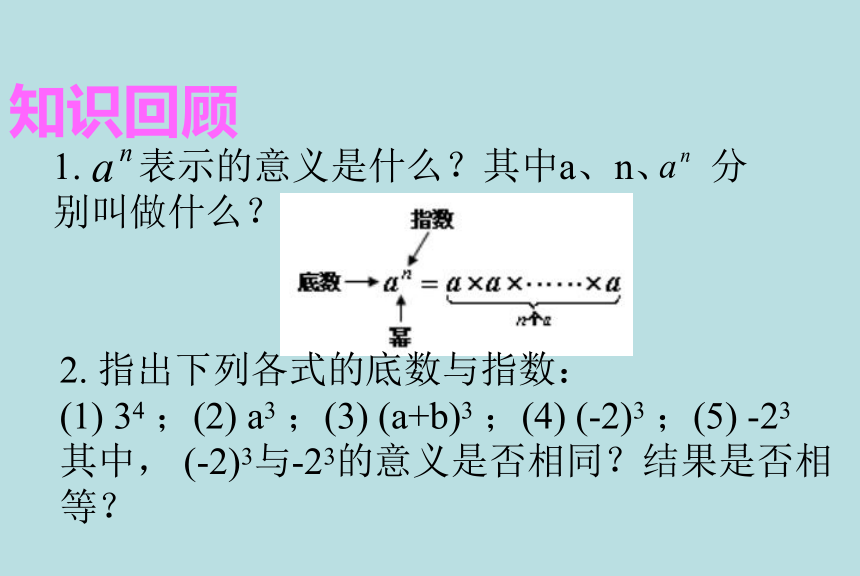
1. 表示的意义是什么?其中a、n、 分别叫做什么?
2. 指出下列各式的底数与指数:
(1) 34 ;(2) a3 ;(3) (a+b)3 ;(4) (-2)3 ;(5) -23
其中, (-2)3与-23的意义是否相同?结果是否相等?
知识回顾
【自主探究】
(10×10×10)×(10×10)
=10×10×10×10×10
=105
(乘方的意义)
(乘法结合律)
(乘方的意义)
1.式子103 ×102 的意义是什么?式中两个因式有何特点?
如何计算?
103 ×102 =
那么, _____, _____.
你发现了什么?
(观察左右两边底数、指数的关系 )
? 呢?(m,n都是正整数)
做一做:
所得结果仍满足以上规律吗?
1013
10m+n
猜想: am · an=? (当m、n都是正整数)
你能验证出你的猜想是否正确吗?
am·an
=am+n
=(a·a· … ·a)(a·a· … ·a)
m个a
n个a
=a·a· … ·a
m+n个a
思考:
同学们,法则中说的是两个同底数幂相乘,那么三个或三个以上同底数幂相乘怎样运算?
结论 :am·an·ap =
am+n+p
(m、n、p都是正整数)
例1:计算
(2)
(4)
(3)
(1)
比一比 、乐一乐:(分组比赛)
规则:(组长上来抽签、读题,组内派
一人回答,并说明理由)
苹果
香蕉
草莓
桔子
梨子
西瓜
苹果
香蕉
草莓
桔子
苹果题:
梨子
西瓜
(1) 76×74
710
x2n+1
(2) x n · xn+1
口算:
苹果
香蕉
草莓
桔子
桔子题:
梨子
西瓜
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( )
(2)b2· b5 = b10 ( )
×
×
b5 · b5= b10
b2 · b5 = b7
苹果
香蕉
草莓
桔子
梨子题:
梨子
西瓜
(1)(-x)2(-x)3(-x)
x6
- 28
(2) (-2)3×25
计算:
苹果
香蕉
草莓
桔子
西瓜题:
梨子
西瓜
0
-29
(1)32×3×9 - 3×34
(2) (-2)2×(-2)7
计算:
苹果
香蕉
草莓
桔子
香蕉题:
梨子
西瓜
已知:am=2, an=3.求am+n =?
解: am+n =
am · an
=2 × 3
=6
苹果
香蕉
草莓
桔子
草莓题:
梨子
西瓜
【中考再现】
(3)已知:an-3×a2n+1=a10,则n=_______
(2)如果2n=2,2m=8,则m+n=____.
4
4
(1)已知x =3, x =5,求x = _____
a
b
a+b
15
谈本节课有哪些收获?
谈在学习本节课内容时应该注意什么?
3.谈本节课学习中还有哪些疑惑?
课堂小结:
1.计算:
2.计算:
3.若 则
4.计算:
(1) (2)
(3) (4)
当 堂 检 测
a5
-a5
120
-x7
220
-a11
(a-1)5
学习目标
1.经历同底数幂的乘法运算性质的过程,能总结出同底数幂乘法的运算性质。
2.能利用同底数幂的乘法运算性质解决相关问题。
1. 表示的意义是什么?其中a、n、 分别叫做什么?
2. 指出下列各式的底数与指数:
(1) 34 ;(2) a3 ;(3) (a+b)3 ;(4) (-2)3 ;(5) -23
其中, (-2)3与-23的意义是否相同?结果是否相等?
知识回顾
【自主探究】
(10×10×10)×(10×10)
=10×10×10×10×10
=105
(乘方的意义)
(乘法结合律)
(乘方的意义)
1.式子103 ×102 的意义是什么?式中两个因式有何特点?
如何计算?
103 ×102 =
那么, _____, _____.
你发现了什么?
(观察左右两边底数、指数的关系 )
? 呢?(m,n都是正整数)
做一做:
所得结果仍满足以上规律吗?
1013
10m+n
猜想: am · an=? (当m、n都是正整数)
你能验证出你的猜想是否正确吗?
am·an
=am+n
=(a·a· … ·a)(a·a· … ·a)
m个a
n个a
=a·a· … ·a
m+n个a
思考:
同学们,法则中说的是两个同底数幂相乘,那么三个或三个以上同底数幂相乘怎样运算?
结论 :am·an·ap =
am+n+p
(m、n、p都是正整数)
例1:计算
(2)
(4)
(3)
(1)
比一比 、乐一乐:(分组比赛)
规则:(组长上来抽签、读题,组内派
一人回答,并说明理由)
苹果
香蕉
草莓
桔子
梨子
西瓜
苹果
香蕉
草莓
桔子
苹果题:
梨子
西瓜
(1) 76×74
710
x2n+1
(2) x n · xn+1
口算:
苹果
香蕉
草莓
桔子
桔子题:
梨子
西瓜
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( )
(2)b2· b5 = b10 ( )
×
×
b5 · b5= b10
b2 · b5 = b7
苹果
香蕉
草莓
桔子
梨子题:
梨子
西瓜
(1)(-x)2(-x)3(-x)
x6
- 28
(2) (-2)3×25
计算:
苹果
香蕉
草莓
桔子
西瓜题:
梨子
西瓜
0
-29
(1)32×3×9 - 3×34
(2) (-2)2×(-2)7
计算:
苹果
香蕉
草莓
桔子
香蕉题:
梨子
西瓜
已知:am=2, an=3.求am+n =?
解: am+n =
am · an
=2 × 3
=6
苹果
香蕉
草莓
桔子
草莓题:
梨子
西瓜
【中考再现】
(3)已知:an-3×a2n+1=a10,则n=_______
(2)如果2n=2,2m=8,则m+n=____.
4
4
(1)已知x =3, x =5,求x = _____
a
b
a+b
15
谈本节课有哪些收获?
谈在学习本节课内容时应该注意什么?
3.谈本节课学习中还有哪些疑惑?
课堂小结:
1.计算:
2.计算:
3.若 则
4.计算:
(1) (2)
(3) (4)
当 堂 检 测
a5
-a5
120
-x7
220
-a11
(a-1)5
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
