北师大版数学七年级下册1.1 同底数幂的乘法课件(21张PPT)
文档属性
| 名称 | 北师大版数学七年级下册1.1 同底数幂的乘法课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 00:00:00 | ||
图片预览







文档简介
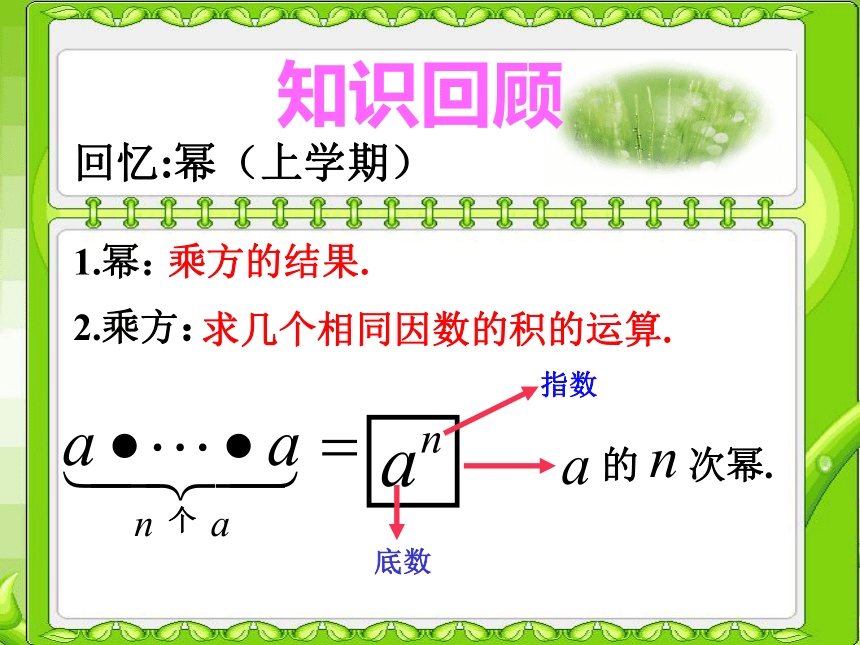
1.幂:
知识回顾
乘方的结果.
个
回忆:幂(上学期)
底数
指数
的 次幂.
求几个相同因数的积的运算.
2.乘方:
10 × 10 等于多少呢?
5
7
问题:光在真空中的速度大约是3×105 千米/秒,太阳系以外距离地球最近的恒星是比邻星,它发出的光到达地球大约需要4.22年。
一年以3×107 秒计算,比邻星与地球的距离约为多少千米?
3×105
×3×107
× 4.22
= 37.98
×(105 ×107 )
个
个
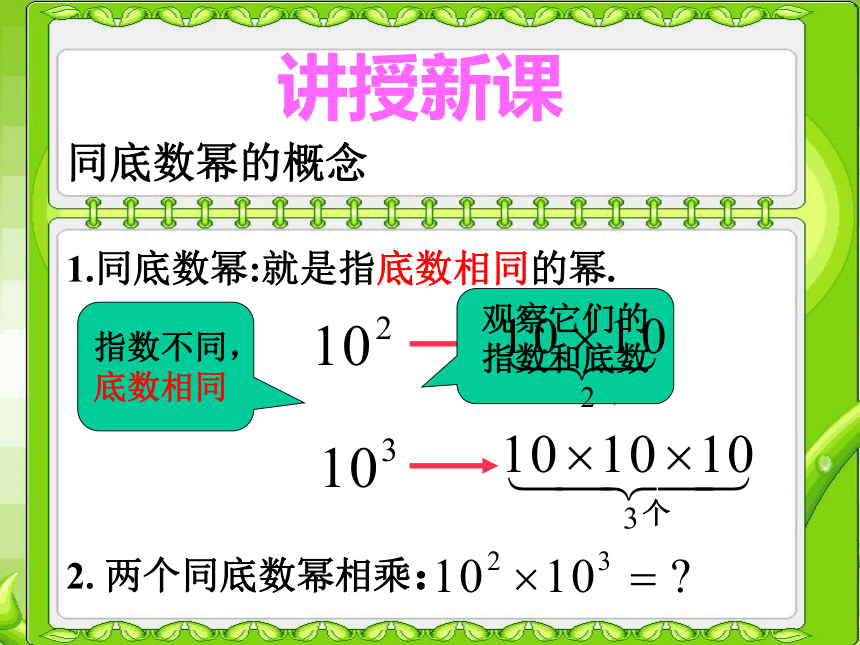
讲授新课
1.同底数幂:就是指底数相同的幂.
2. 两个同底数幂相乘:
指数不同,底数相同
同底数幂的概念
观察它们的指数和底数
讲授新课
1. 两个同底数幂相乘:
(乘方的意义)
(乘法结合律)
(乘方的意义)
探索:同底数幂的乘法法则
解:
继续探索:
将上题中的底数10改为任意底数 ,则有
个
个
个
如果我把上题中的指数 3,2改成一般的任意正整数并分别用字母 来表示.
同底数幂的乘法法则:
( 都是正整数)
即:同底数幂相乘,底数_____,指数______.
不变
相加
幂的底数必须相同,
相乘时指数才能相加。
开始的例题计算结果
3×105
×3×107
× 4.22
= 37.98
×(105 ×107 )
计算:
解
计算:
解
(3)(x+y) ( x+y)=
3
(x+y)
3+1
=(x+y)
4
(x+y) ( x+y)
3
(3)
下面的计算结果对不对?如果不对,怎样改正?
1、b5 · b5= 2b5 ( ) 2、b5 + b5 = b10 ( )
b5 · b5= b10
b5 + b5 = 2b5
×
×
抢答练习
计算:
(1011 )
( a10 )
( x10 )
( b6 )
(2) a7 ·a3
(3) x5 ·x5
(4) b5 · b
(1) 105×106
(5)10×102×104
(107)
(6) y4·y3·y2·y
(y10)
公式推广:一
当三个或三个以上的同底数幂相乘时,法则可以推广为:
( 都是正整数)
即:当幂与幂之间相乘时,只要是底数相同,就可以直接利用同底数幂的乘法法则:底数不变,指数相加.
计算:
解
注意:y的指数是“1”,而不是“0”
小组练习(展示) 计算:
原式=
原式=
原式=
注意:
计算时要先观察底数是否相同,不同底的要先化为同底的才可以运用法则.
公式推广:二
am+n= am · an (m,n都是正整数)
公式逆用:
已知 =4, =3,求下列各式的值。
a
m
a
n
(1)
a
m+n
(2)
a
3+n
(3)
a
m+n+2
解:
(1)
a
m+n
(2)
a
3+n
(3)
a
m+n+2
=4×3=12
a
n
?
a
m
=
a
3
a
n
=
×
=3a
3
a
m
a
n
a
2
=
×
×
a
2
=
4×3×
a
2
=12
am+n=am ?an
点拨:同底数幂乘法公式的逆用也很重要.
练习:
同底数幂相乘,底数不变,指数相加.
同底数幂的乘法:
( 都是正整数)
( 都是正整数)
今天,我们学到了什么?
课堂小结
再见
知识回顾
乘方的结果.
个
回忆:幂(上学期)
底数
指数
的 次幂.
求几个相同因数的积的运算.
2.乘方:
10 × 10 等于多少呢?
5
7
问题:光在真空中的速度大约是3×105 千米/秒,太阳系以外距离地球最近的恒星是比邻星,它发出的光到达地球大约需要4.22年。
一年以3×107 秒计算,比邻星与地球的距离约为多少千米?
3×105
×3×107
× 4.22
= 37.98
×(105 ×107 )
个
个
讲授新课
1.同底数幂:就是指底数相同的幂.
2. 两个同底数幂相乘:
指数不同,底数相同
同底数幂的概念
观察它们的指数和底数
讲授新课
1. 两个同底数幂相乘:
(乘方的意义)
(乘法结合律)
(乘方的意义)
探索:同底数幂的乘法法则
解:
继续探索:
将上题中的底数10改为任意底数 ,则有
个
个
个
如果我把上题中的指数 3,2改成一般的任意正整数并分别用字母 来表示.
同底数幂的乘法法则:
( 都是正整数)
即:同底数幂相乘,底数_____,指数______.
不变
相加
幂的底数必须相同,
相乘时指数才能相加。
开始的例题计算结果
3×105
×3×107
× 4.22
= 37.98
×(105 ×107 )
计算:
解
计算:
解
(3)(x+y) ( x+y)=
3
(x+y)
3+1
=(x+y)
4
(x+y) ( x+y)
3
(3)
下面的计算结果对不对?如果不对,怎样改正?
1、b5 · b5= 2b5 ( ) 2、b5 + b5 = b10 ( )
b5 · b5= b10
b5 + b5 = 2b5
×
×
抢答练习
计算:
(1011 )
( a10 )
( x10 )
( b6 )
(2) a7 ·a3
(3) x5 ·x5
(4) b5 · b
(1) 105×106
(5)10×102×104
(107)
(6) y4·y3·y2·y
(y10)
公式推广:一
当三个或三个以上的同底数幂相乘时,法则可以推广为:
( 都是正整数)
即:当幂与幂之间相乘时,只要是底数相同,就可以直接利用同底数幂的乘法法则:底数不变,指数相加.
计算:
解
注意:y的指数是“1”,而不是“0”
小组练习(展示) 计算:
原式=
原式=
原式=
注意:
计算时要先观察底数是否相同,不同底的要先化为同底的才可以运用法则.
公式推广:二
am+n= am · an (m,n都是正整数)
公式逆用:
已知 =4, =3,求下列各式的值。
a
m
a
n
(1)
a
m+n
(2)
a
3+n
(3)
a
m+n+2
解:
(1)
a
m+n
(2)
a
3+n
(3)
a
m+n+2
=4×3=12
a
n
?
a
m
=
a
3
a
n
=
×
=3a
3
a
m
a
n
a
2
=
×
×
a
2
=
4×3×
a
2
=12
am+n=am ?an
点拨:同底数幂乘法公式的逆用也很重要.
练习:
同底数幂相乘,底数不变,指数相加.
同底数幂的乘法:
( 都是正整数)
( 都是正整数)
今天,我们学到了什么?
课堂小结
再见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
