北师大版数学七年级下册第1章3 同底数幂的除法(共17张PPT)
文档属性
| 名称 | 北师大版数学七年级下册第1章3 同底数幂的除法(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 596.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 21:11:31 | ||
图片预览




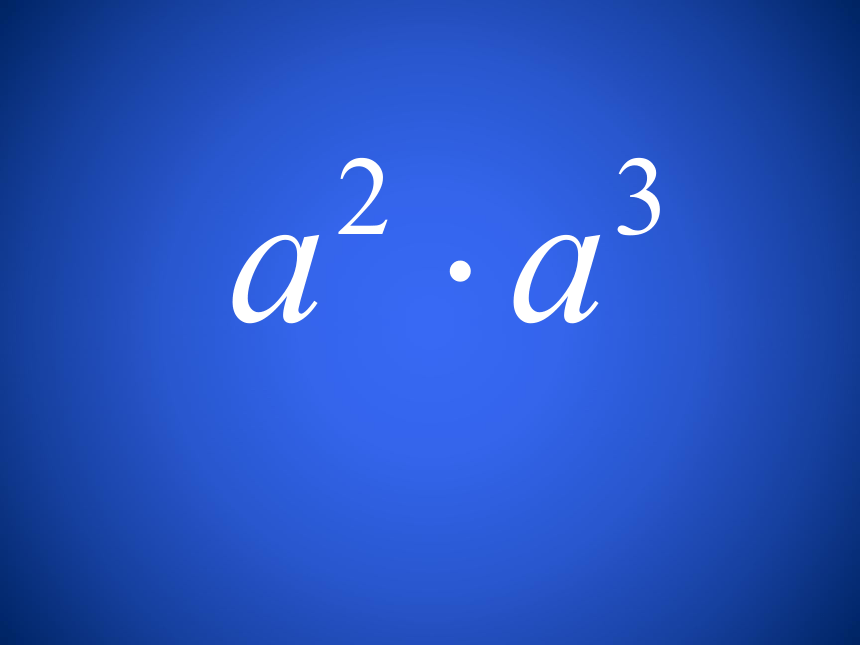

文档简介
第一章 整式的乘除
同底数幂的乘法
3 同底数幂的除法
探究活动:下面有四个整式,判断它们分别是单项式还是多项式?
(2)试着将写出来的算式分类,你认为整式的乘法可以分为哪几种类型?(用序号分类)
(1)并从中任选两个构造乘法
运算。你能写出哪些算式?
单
单
多
多
单项式乘以单项式:
单项式乘以多项式:
多项式乘以多项式:
a
n
指数
幂
= a·a· … ·a
n个a
底数
探究新知
1.根据乘方的意义计算下列各式:
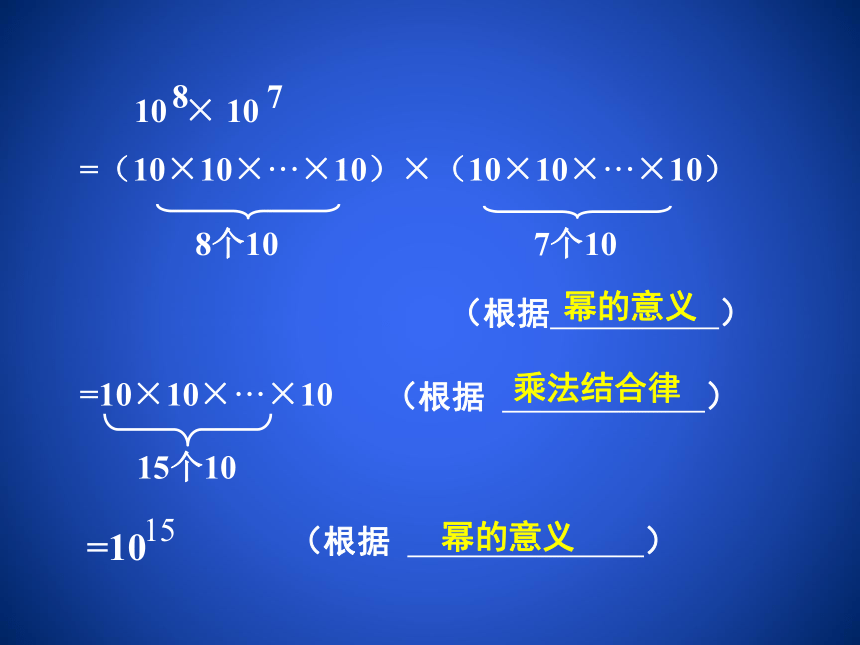
(1)108×107;
(2)25×26;
(3)a5×a2;
(4)
10 × 10
8
7
=(10×10×···×10)×(10×10×···×10)
8个10
7个10
=10×10×···×10
15个10
=10
15
幂的意义
幂的意义
(根据 )
(根据 )
(根据 )
乘法结合律
探究新知
1.根据乘方的意义计算下列各式:
(1)108×107;
(2)25×26;
(3)a5×a2;
(4)
通过以上的计算,你能发现什么规律吗?
探究新知
am · an (m,n都是正整数)
=am+n
不变
相加
=am+n
探究新知
同底数幂相乘,底数 ,指数 .
即
底数不变
指数相加
不变
相加
条件
结论
(1.同底;2.乘法)
(底不变、指相加)
应用法则 巩固落实
1.辨一辩:下列各式,哪些是同底数幂的乘法?并说出计算结果。
(1) x4·x6= ( )
(2)(-2)3×(-2)5= ( )
(3) x4+x4= ( )
(4) x3·y5= ( )
(5)
( )
am· an· ap = am+n+p
am· an· ap = am+n+p
想一想:把(1)给成x4·x6·x5,如何计算呢?
是
是
是
不是
不是
2x4
x10
28
(a+b)5
依据:负数的奇次
幂是负数,
负数的偶次幂是正数。
① x3·x4=x12 ②
③ x2·x2=2x4 ④
⑤23×(-2)6 =29 ⑥
2.判一判:下面计算对吗?如果不对,怎么改正?
应用法则 巩固落实
x3·x2·x=x5
26
依据:负数的奇次幂是负数,
负数的偶次幂是正数。
m2
m4
x7
x6
x4
3.算一算:计算下列各式,结果用幂的形式表示。
应用法则 巩固落实
4.用一用
一个长方体的长为4×103厘米,宽为2×102厘米,高为2.5×103厘米,求它的体积是多少?(结果用科学记数法表示).
应用法则 巩固落实
如果改为 ,该怎么计算这个式子?
想一想:如果将上式中的部分数字改为字母,比如: ,该怎么计算这个式子?
回顾一下:
(1)发现了一个什么新法则?
(2)我们是怎么发现的?
(3)运用这个法则要注意什么问题?
小结
小结
加减运算
乘法运算
……
请为同底数幂的乘法安个“家”
单项式乘单项式
单项式乘多项式
多项式乘多项式
整式的运算
作业
完成课本习题1.1中所有习题
拓展作业:
你能尝试运用今天所学的同底数幂的乘法解决下面的问题吗
同底数幂的乘法
3 同底数幂的除法
探究活动:下面有四个整式,判断它们分别是单项式还是多项式?
(2)试着将写出来的算式分类,你认为整式的乘法可以分为哪几种类型?(用序号分类)
(1)并从中任选两个构造乘法
运算。你能写出哪些算式?
单
单
多
多
单项式乘以单项式:
单项式乘以多项式:
多项式乘以多项式:
a
n
指数
幂
= a·a· … ·a
n个a
底数
探究新知
1.根据乘方的意义计算下列各式:
(1)108×107;
(2)25×26;
(3)a5×a2;
(4)
10 × 10
8
7
=(10×10×···×10)×(10×10×···×10)
8个10
7个10
=10×10×···×10
15个10
=10
15
幂的意义
幂的意义
(根据 )
(根据 )
(根据 )
乘法结合律
探究新知
1.根据乘方的意义计算下列各式:
(1)108×107;
(2)25×26;
(3)a5×a2;
(4)
通过以上的计算,你能发现什么规律吗?
探究新知
am · an (m,n都是正整数)
=am+n
不变
相加
=am+n
探究新知
同底数幂相乘,底数 ,指数 .
即
底数不变
指数相加
不变
相加
条件
结论
(1.同底;2.乘法)
(底不变、指相加)
应用法则 巩固落实
1.辨一辩:下列各式,哪些是同底数幂的乘法?并说出计算结果。
(1) x4·x6= ( )
(2)(-2)3×(-2)5= ( )
(3) x4+x4= ( )
(4) x3·y5= ( )
(5)
( )
am· an· ap = am+n+p
am· an· ap = am+n+p
想一想:把(1)给成x4·x6·x5,如何计算呢?
是
是
是
不是
不是
2x4
x10
28
(a+b)5
依据:负数的奇次
幂是负数,
负数的偶次幂是正数。
① x3·x4=x12 ②
③ x2·x2=2x4 ④
⑤23×(-2)6 =29 ⑥
2.判一判:下面计算对吗?如果不对,怎么改正?
应用法则 巩固落实
x3·x2·x=x5
26
依据:负数的奇次幂是负数,
负数的偶次幂是正数。
m2
m4
x7
x6
x4
3.算一算:计算下列各式,结果用幂的形式表示。
应用法则 巩固落实
4.用一用
一个长方体的长为4×103厘米,宽为2×102厘米,高为2.5×103厘米,求它的体积是多少?(结果用科学记数法表示).
应用法则 巩固落实
如果改为 ,该怎么计算这个式子?
想一想:如果将上式中的部分数字改为字母,比如: ,该怎么计算这个式子?
回顾一下:
(1)发现了一个什么新法则?
(2)我们是怎么发现的?
(3)运用这个法则要注意什么问题?
小结
小结
加减运算
乘法运算
……
请为同底数幂的乘法安个“家”
单项式乘单项式
单项式乘多项式
多项式乘多项式
整式的运算
作业
完成课本习题1.1中所有习题
拓展作业:
你能尝试运用今天所学的同底数幂的乘法解决下面的问题吗
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
