沪教版(上海)初中数学七年级第一学期 9.1 用字母表示数 课件(共31张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 9.1 用字母表示数 课件(共31张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 07:07:22 | ||
图片预览










文档简介
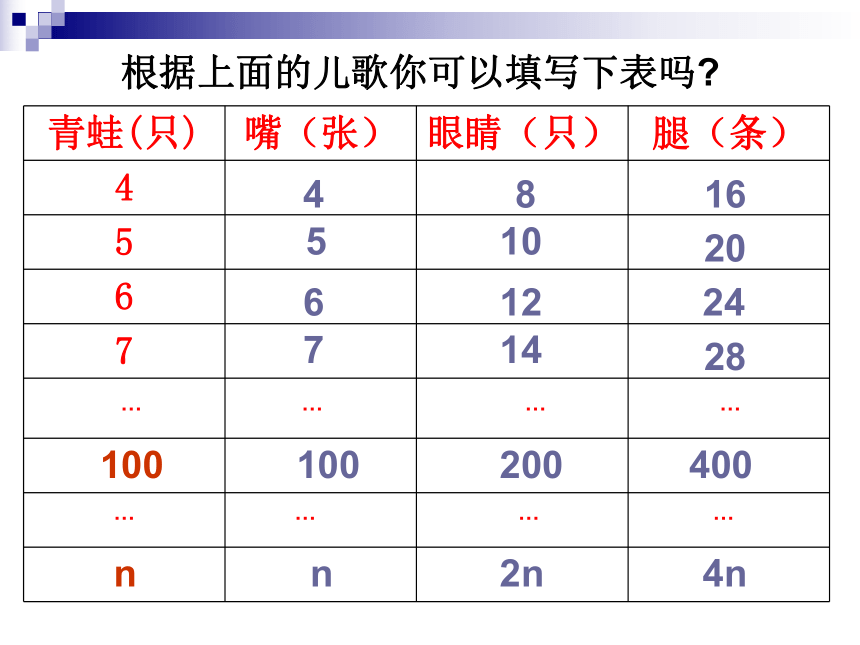
根据上面的儿歌你可以填写下表吗?
青蛙(只)
嘴(张)
眼睛(只)
腿(条)
4
5
6
7
4
… … … …
8
16
5
24
20
6
10
12
2n
n
400
200
100
28
14
7
4n
100
n
… … … …
3.1用字母表示数
字母和字母相乘时,乘号可以省略不写 。
(1)练习簿的单价为a元,100本练习簿的总价是______元。
(2)练习簿的单价为a元,b本练习簿的总价是_____元。
100a
ab
数和字母相乘,省略乘号,并把数写在字母的前面 。
后面接单位的相加(减)的式子要用括号括起来。
(3)练习簿的单价为a元,圆珠笔的单价是b元,买10本练习簿和5支圆珠笔的总价是 _______ 元。
10a+5b
( )
(4)小明的家离学校s千米,小明骑车上学.若每小时行10千米,则需______小时。
除法运算写成分数形式
s
10
(5)买 1 千克苹果,每千克m元,则共花了 _______元。
3
1
带分数与字母相乘时,带分数要写成假分数的形式。
1
1
3
m
(6)气温每小时上升1 度,则m小时后温度上升______度.
气温每小时上升-1度,则n小时后温度上升______度。
1和-1同字母相乘时,1省略不写。
1m
-1n
m
-n
1、表示数与字母相乘,或字母和字母相乘时,乘号可以省略不写,数和字母相乘,在省略乘号时,要把数字写在字母的前面,如n×2应写成2n,不能写成n2;
2、带分数与字母相乘时,带分数要写成假分数的形式。
3、 1和-1同字母相乘时,1省略不写。
4、除法运算要写成分数形式。
5、后面有单位的相加(减)的式子要用括号括起来。
你能归纳用字母表示数的书写要领吗?
“数”前“母”后
、乘号省略
逢“带”化“假”
练一练
(1)长方形的长是a米,宽是3米,则面积是_____平方米.
(2)小明每小时走v千米, 小时走_______千米.
1
1
2
3
2
v
3a
(4)设奶粉每袋p元,桔子每袋q元,则买10袋奶粉、6袋桔子共需_______ 元。
(3) 小明的家离学校s千米,小明骑车上学. 若每小时行v千米,则需_____时;
s
v
(10p+6q )
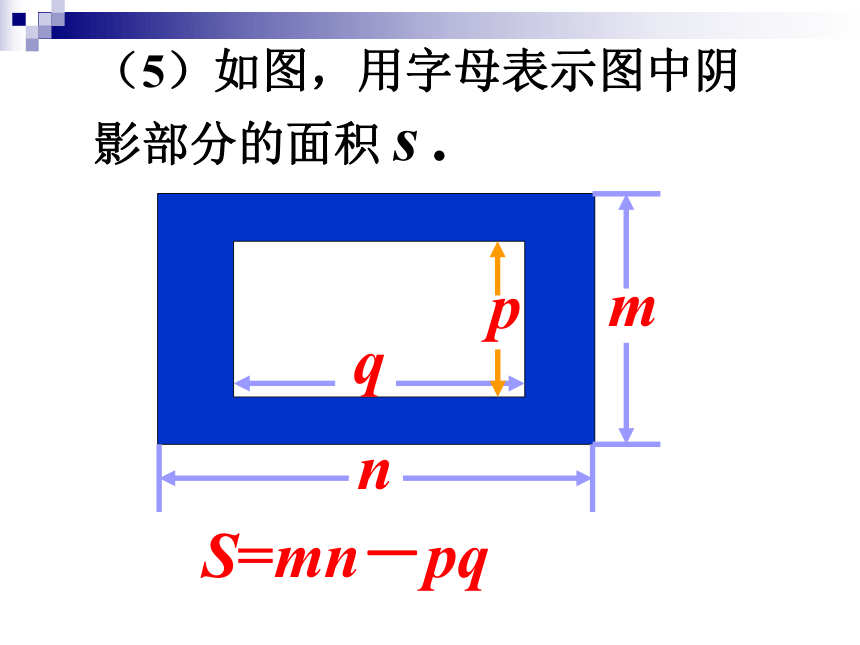
(5)如图,用字母表示图中阴影部分的面积 s .
p
q
m
n
S=mn-pq
1、m的 倍可以用 表示。
2、-a一定是负数。
4、a+1一定大于1。
判断题
×
×
×
3、m的绝对值大于或等于m。
√
我们在以前的学习中在哪些地方曾用到字母表示数?
这些字母表示的是什么数?
2+3=3+2,
0+(-7)=(-7)+0,
-6+2=2+(-6),
……
你能用文字语言表示下面各式的规律吗?
两个数相加,交换加数的位置,它们的和不变。
加法交换律
2+3=3+2,
0+(-7)=(-7)+0,
-6+2=2+(-6),
……
你能用含字母的式子表示下面各式的规律吗?
a+b=b+a
加法交换律
1、用a,b,c表示三个数,那么数的运算律可表示为
加法的交换律
加法的结合律
乘法的交换律
乘法的结合律
乘法的分配律
a+b=b+a
(a+b)+c=a+(b+c)
ab=ba
(ab)c=a(bc)
(a+b)c=ac+bc
字母可以用来表示数的运算定律。
2.周长公式:
a
b
r
c
b
a
c
b
d
a
2a+2b
2πr
a+b+c+d
a+b+c
a
a
4a
3.面积公式:
a
b
r
a
a
a
h
b
a
h
h
a
4.行程问题公式:
S=vt
t=
s
—
v
v=
s
—
t
字母可以用来表示图形的周长、面积等公式或其他确定的数量关系。
3.面积公式:
a
b
r
a
a
a
h
b
a
h
h
a
4.行程问题公式:
S=vt
t=
s
—
v
v=
s
—
t
字母可以用来表示图形的周长、面积等公式或其他确定的数量关系。
……
正方形的个数
所用火柴棒的根数
1
2
3
……
20
……
n
4
7
10
61
……
……
按照如图所示的方式用火柴棒撘正方形。
……
搭n个这样的正方形需要多少这样的火柴棒?你是怎么想的?
探索规律
4+3(n-1)
(用火柴棒拼n个正方形)
……
(n-1)个
探索规律
n+n+(n+1)
(用火柴棒拼n个正方形)
……
n根
n根
探索规律
探索规律
(用火柴棒拼n个正方形)
1+3n
……
n个
4n-(n-1)
(用火柴棒拼n个正方形)
探索规律
……
n个
(n-1)个
根据你们的方法,搭200个这样的正方形需要多少根火柴棒?
4+3(n-1)
n+n+(n+1)
1+3n
4n-(n-1)
601根
……
……
……
……
……
(1)请你观察月历中涂色框中的3个数有什么关系?
如果我们用字母a表示方框中的一个数,那么其余的2个数怎样用a来表示?
a
a
a
(2)如果涂色框中是如图的4个数呢?你会用用字母把它们的关系表示出来吗?
(1)、用字母表示数能简明、具有普遍意义地表示数量关系;
(2)、在用字母表示数时要注意书写格式。
(3)、用字母表示数能为我们探索规律提供方便。
1、小明今年14岁, a年前小明 岁。
(14-a)
n+1
2、有两个连续的自然数,较小的一个是n,
则较大的一个是 。
2n
3、偶数用 表示,奇数用 表示。
4、已知实数a(a≠0),则a的倒数是__,
a的相反数是__ ,a的绝对值是 ,
a与-4的差是 。
-a
2n+1
a-(-4)
5、一个两位数,各位数字是a,十位数字是b,
则这个数是 。
10b+a
青蛙(只)
嘴(张)
眼睛(只)
腿(条)
4
5
6
7
4
… … … …
8
16
5
24
20
6
10
12
2n
n
400
200
100
28
14
7
4n
100
n
… … … …
3.1用字母表示数
字母和字母相乘时,乘号可以省略不写 。
(1)练习簿的单价为a元,100本练习簿的总价是______元。
(2)练习簿的单价为a元,b本练习簿的总价是_____元。
100a
ab
数和字母相乘,省略乘号,并把数写在字母的前面 。
后面接单位的相加(减)的式子要用括号括起来。
(3)练习簿的单价为a元,圆珠笔的单价是b元,买10本练习簿和5支圆珠笔的总价是 _______ 元。
10a+5b
( )
(4)小明的家离学校s千米,小明骑车上学.若每小时行10千米,则需______小时。
除法运算写成分数形式
s
10
(5)买 1 千克苹果,每千克m元,则共花了 _______元。
3
1
带分数与字母相乘时,带分数要写成假分数的形式。
1
1
3
m
(6)气温每小时上升1 度,则m小时后温度上升______度.
气温每小时上升-1度,则n小时后温度上升______度。
1和-1同字母相乘时,1省略不写。
1m
-1n
m
-n
1、表示数与字母相乘,或字母和字母相乘时,乘号可以省略不写,数和字母相乘,在省略乘号时,要把数字写在字母的前面,如n×2应写成2n,不能写成n2;
2、带分数与字母相乘时,带分数要写成假分数的形式。
3、 1和-1同字母相乘时,1省略不写。
4、除法运算要写成分数形式。
5、后面有单位的相加(减)的式子要用括号括起来。
你能归纳用字母表示数的书写要领吗?
“数”前“母”后
、乘号省略
逢“带”化“假”
练一练
(1)长方形的长是a米,宽是3米,则面积是_____平方米.
(2)小明每小时走v千米, 小时走_______千米.
1
1
2
3
2
v
3a
(4)设奶粉每袋p元,桔子每袋q元,则买10袋奶粉、6袋桔子共需_______ 元。
(3) 小明的家离学校s千米,小明骑车上学. 若每小时行v千米,则需_____时;
s
v
(10p+6q )
(5)如图,用字母表示图中阴影部分的面积 s .
p
q
m
n
S=mn-pq
1、m的 倍可以用 表示。
2、-a一定是负数。
4、a+1一定大于1。
判断题
×
×
×
3、m的绝对值大于或等于m。
√
我们在以前的学习中在哪些地方曾用到字母表示数?
这些字母表示的是什么数?
2+3=3+2,
0+(-7)=(-7)+0,
-6+2=2+(-6),
……
你能用文字语言表示下面各式的规律吗?
两个数相加,交换加数的位置,它们的和不变。
加法交换律
2+3=3+2,
0+(-7)=(-7)+0,
-6+2=2+(-6),
……
你能用含字母的式子表示下面各式的规律吗?
a+b=b+a
加法交换律
1、用a,b,c表示三个数,那么数的运算律可表示为
加法的交换律
加法的结合律
乘法的交换律
乘法的结合律
乘法的分配律
a+b=b+a
(a+b)+c=a+(b+c)
ab=ba
(ab)c=a(bc)
(a+b)c=ac+bc
字母可以用来表示数的运算定律。
2.周长公式:
a
b
r
c
b
a
c
b
d
a
2a+2b
2πr
a+b+c+d
a+b+c
a
a
4a
3.面积公式:
a
b
r
a
a
a
h
b
a
h
h
a
4.行程问题公式:
S=vt
t=
s
—
v
v=
s
—
t
字母可以用来表示图形的周长、面积等公式或其他确定的数量关系。
3.面积公式:
a
b
r
a
a
a
h
b
a
h
h
a
4.行程问题公式:
S=vt
t=
s
—
v
v=
s
—
t
字母可以用来表示图形的周长、面积等公式或其他确定的数量关系。
……
正方形的个数
所用火柴棒的根数
1
2
3
……
20
……
n
4
7
10
61
……
……
按照如图所示的方式用火柴棒撘正方形。
……
搭n个这样的正方形需要多少这样的火柴棒?你是怎么想的?
探索规律
4+3(n-1)
(用火柴棒拼n个正方形)
……
(n-1)个
探索规律
n+n+(n+1)
(用火柴棒拼n个正方形)
……
n根
n根
探索规律
探索规律
(用火柴棒拼n个正方形)
1+3n
……
n个
4n-(n-1)
(用火柴棒拼n个正方形)
探索规律
……
n个
(n-1)个
根据你们的方法,搭200个这样的正方形需要多少根火柴棒?
4+3(n-1)
n+n+(n+1)
1+3n
4n-(n-1)
601根
……
……
……
……
……
(1)请你观察月历中涂色框中的3个数有什么关系?
如果我们用字母a表示方框中的一个数,那么其余的2个数怎样用a来表示?
a
a
a
(2)如果涂色框中是如图的4个数呢?你会用用字母把它们的关系表示出来吗?
(1)、用字母表示数能简明、具有普遍意义地表示数量关系;
(2)、在用字母表示数时要注意书写格式。
(3)、用字母表示数能为我们探索规律提供方便。
1、小明今年14岁, a年前小明 岁。
(14-a)
n+1
2、有两个连续的自然数,较小的一个是n,
则较大的一个是 。
2n
3、偶数用 表示,奇数用 表示。
4、已知实数a(a≠0),则a的倒数是__,
a的相反数是__ ,a的绝对值是 ,
a与-4的差是 。
-a
2n+1
a-(-4)
5、一个两位数,各位数字是a,十位数字是b,
则这个数是 。
10b+a
