沪教版(上海)数学八年级第二学期-22.3 特殊的平行四边形(1) 课件(共21张PPT)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.3 特殊的平行四边形(1) 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 21:19:46 | ||
图片预览





文档简介
三角形
有一个角是直角
有两条边相等
直角三角形
等腰三角形
特殊的三角形是从任意三角形的边或角所具有的特征来定义的.
有一个角是直角
有一组邻边相等
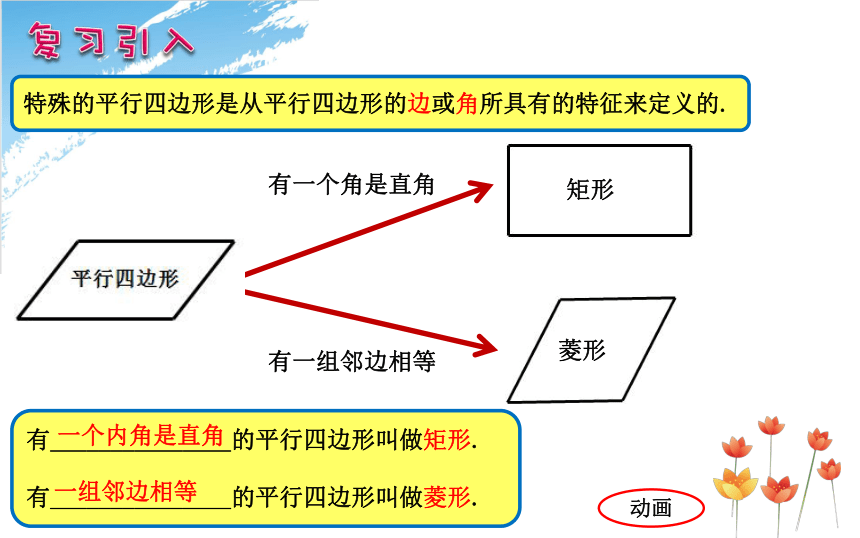
特殊的平行四边形是从平行四边形的边或角所具有的特征来定义的.
矩形
菱形
有_______________的平行四边形叫做矩形.
有_______________的平行四边形叫做菱形.
一个内角是直角
一组邻边相等
动画
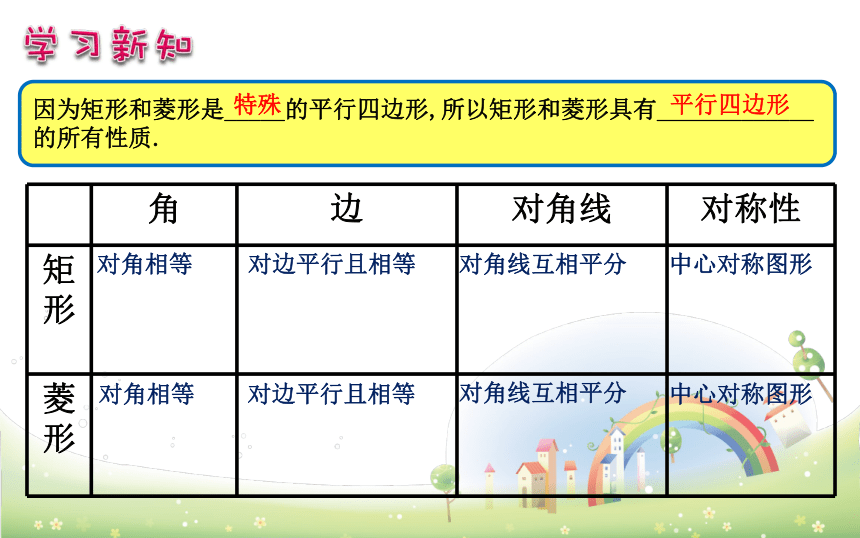
因为矩形和菱形是_____的平行四边形,所以矩形和菱形具有_____________的所有性质.
特殊
平行四边形
角
边
对角线
对称性
矩形
菱形
对边平行且相等
对边平行且相等
对角相等
对角线互相平分
对角线互相平分
中心对称图形
中心对称图形
对角相等
根据矩形的定义想一想矩形的角有什么特殊的性质?
∵四边形ABCD是矩形,设∠A=90°.
另外三
个角呢?
∵矩形ABCD是平行四边形,
∴AD∥BC(平行四边形的对边平行),
∴∠A+∠B=180°,
∴∠B=90°.
同理,∠C=∠D=90°.
矩形的性质定理1:矩形的四个角都是直角..
符号语言:
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°
(矩形的四个角都是直角).
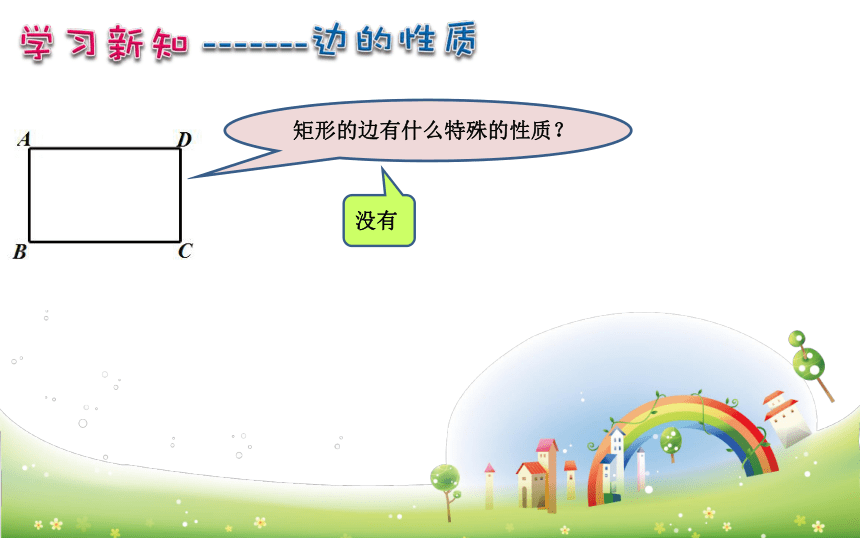
没有
菱形的角有什么特殊的性质?
矩形的边有什么特殊的性质?
没有
∵四边形ABCD是菱形,设AB=BC.
另外两条边呢?
∵菱形ABCD是平行四边形,
∴AD=BC,AB=DC(平行四边形的对边相等),
∴AD=AB=BC=DC.
菱形的性质定理1:菱形的四条边都相等..
符号语言:
∵四边形ABCD是菱形,
∴AD=AB=BC=DC
(菱形的四条边都相等).
根据菱形的定义想一想菱形的边有什么特殊的性质?
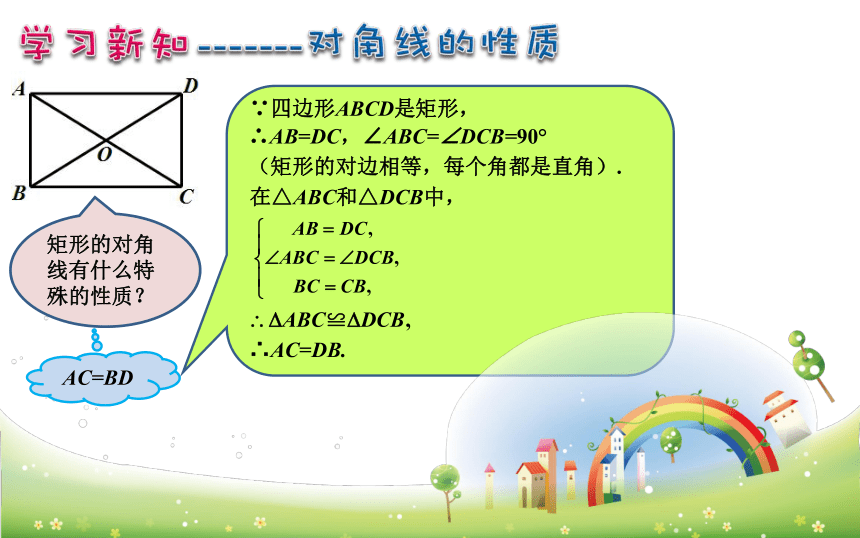
矩形的对角线有什么特殊的性质?
AC=BD
∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°
(矩形的对边相等,每个角都是直角).
在△ABC和△DCB中,
∴AC=DB.
∵四边形ABCD是矩形,
(矩形的对角线相等).
∴AC=DB
矩形的性质定理2:矩形的对角线相等..
符号语言:
AC⊥BD
∵四边形ABCD是菱形,
∴AB=AD,BO=DO
(菱形的四条边都相等,对角线互相平分).
∴AC⊥BD,AC平分∠BAD.
菱形的对角线有什么特殊的性质?
AC平分∠BAD、∠BCD
BD平分∠ABC、∠ADC
同理,AC平分∠BCD
BD平分∠ABC、∠ADC.
∵四边形ABCD是菱形
(菱形的对角线互相垂直,并且每一条对角线平分一组对角).
∴AC⊥DB
菱形的性质定理2:菱形的对角线互相垂直,并且每一条对角线平分
一组对角..
符号语言:
∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8
矩形、菱形是轴对称图形吗?
矩形是轴对称图形,有2条对称轴,是经过任意一组对边中点的直线.
菱形是轴对称图形,有2条对称轴,是任意一条对角线所在的直线.
角
边
对角线
对称性
矩形
菱形
对边平行且相等
对边平行
对角相等
对角线互相平分
对角线互相平分
中心对称图形
中心对称图形
对角相等
矩形、菱形的性质:
每个角都
是直角
且相等.
轴对称图形
且相等
四条边都相等
且互相垂直,每一条对角线平分一组对角.
轴对称图形
例题1 如图,矩形ABCD的对角线AC与BD相交于点O,已知∠AOD=120°,AB=4cm,求AC、BD的长.
解:∵四边形ABCD是矩形,
(平行四边形的对角线互相平分),
∴AC=BD(矩形的对角线相等).
∴AO=BO.
∵∠1=120°,
∴∠2=60°.
∴△ABO是等边三角形.
∵AB=4cm,
∴OA=OB=4cm.
矩形的对角线有什么特征?
还能知道哪个角的度数?
那么△AOB是什么三角形?
等边
三角形
∴AC=BD=8cm.
AC=BD,
OA=OC,OB=OD.
矩形的两条对角线把矩形分成四个______的三角形.
等腰
如果两条对角线的夹角为60°,那么60°角所在的两个等腰三角形是_______三角形.
等边
1、根据图形求出相应的x、y的值(第1、3个图是矩形,第2个图是菱形;第3个图中的2x、2y+4、x+3y分别表示矩形对角线一半的长):
以上3题都是将几何问题转化为代数问题来解决的.
2、下列命题中假命题是( )
(A)矩形的对角线互相平分且相等;
(B)菱形的对角线互相平分且垂直;
(C)矩形的两条对角线把矩形分成四个直角三角形;
(D)菱形的两条对角线把菱形分成四个直角三角形;
C
3、利用矩形的性质,证明:直角三角形斜边上的中线等于斜边的一半.
已知:在Rt△ABC中,∠ACB=90°点D是斜边AB的中点.
求证:
E
证明:延长CD到点E,使得DE=CD,联结AE、BE.
∵点D是斜边AB的中点,
∴四边形ACBE是平行四边形
(对角线互相平分的四边形是平行四边形).
又∵ ∠ACB=90°,
∴四边形ACBE是矩形(有一个角是直角的平行四边形是矩形).
∴AB=CE(矩形的对角线相等).
∴
1、矩形、菱形的定义
有一个角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
2、矩形、菱形的性质
角
边
对角线
对称性
矩形
菱形
对边平行且相等
对角相等
对角线互相平分且相等.
对角线互相平分且互相垂直,每一条对角线平分一组对角.
中心对称图形
中心对称图形
每个角都
是直角
轴对称图形
四条边都相等
轴对称图形
对边平行
有一个角是直角
有两条边相等
直角三角形
等腰三角形
特殊的三角形是从任意三角形的边或角所具有的特征来定义的.
有一个角是直角
有一组邻边相等
特殊的平行四边形是从平行四边形的边或角所具有的特征来定义的.
矩形
菱形
有_______________的平行四边形叫做矩形.
有_______________的平行四边形叫做菱形.
一个内角是直角
一组邻边相等
动画
因为矩形和菱形是_____的平行四边形,所以矩形和菱形具有_____________的所有性质.
特殊
平行四边形
角
边
对角线
对称性
矩形
菱形
对边平行且相等
对边平行且相等
对角相等
对角线互相平分
对角线互相平分
中心对称图形
中心对称图形
对角相等
根据矩形的定义想一想矩形的角有什么特殊的性质?
∵四边形ABCD是矩形,设∠A=90°.
另外三
个角呢?
∵矩形ABCD是平行四边形,
∴AD∥BC(平行四边形的对边平行),
∴∠A+∠B=180°,
∴∠B=90°.
同理,∠C=∠D=90°.
矩形的性质定理1:矩形的四个角都是直角..
符号语言:
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°
(矩形的四个角都是直角).
没有
菱形的角有什么特殊的性质?
矩形的边有什么特殊的性质?
没有
∵四边形ABCD是菱形,设AB=BC.
另外两条边呢?
∵菱形ABCD是平行四边形,
∴AD=BC,AB=DC(平行四边形的对边相等),
∴AD=AB=BC=DC.
菱形的性质定理1:菱形的四条边都相等..
符号语言:
∵四边形ABCD是菱形,
∴AD=AB=BC=DC
(菱形的四条边都相等).
根据菱形的定义想一想菱形的边有什么特殊的性质?
矩形的对角线有什么特殊的性质?
AC=BD
∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°
(矩形的对边相等,每个角都是直角).
在△ABC和△DCB中,
∴AC=DB.
∵四边形ABCD是矩形,
(矩形的对角线相等).
∴AC=DB
矩形的性质定理2:矩形的对角线相等..
符号语言:
AC⊥BD
∵四边形ABCD是菱形,
∴AB=AD,BO=DO
(菱形的四条边都相等,对角线互相平分).
∴AC⊥BD,AC平分∠BAD.
菱形的对角线有什么特殊的性质?
AC平分∠BAD、∠BCD
BD平分∠ABC、∠ADC
同理,AC平分∠BCD
BD平分∠ABC、∠ADC.
∵四边形ABCD是菱形
(菱形的对角线互相垂直,并且每一条对角线平分一组对角).
∴AC⊥DB
菱形的性质定理2:菱形的对角线互相垂直,并且每一条对角线平分
一组对角..
符号语言:
∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8
矩形、菱形是轴对称图形吗?
矩形是轴对称图形,有2条对称轴,是经过任意一组对边中点的直线.
菱形是轴对称图形,有2条对称轴,是任意一条对角线所在的直线.
角
边
对角线
对称性
矩形
菱形
对边平行且相等
对边平行
对角相等
对角线互相平分
对角线互相平分
中心对称图形
中心对称图形
对角相等
矩形、菱形的性质:
每个角都
是直角
且相等.
轴对称图形
且相等
四条边都相等
且互相垂直,每一条对角线平分一组对角.
轴对称图形
例题1 如图,矩形ABCD的对角线AC与BD相交于点O,已知∠AOD=120°,AB=4cm,求AC、BD的长.
解:∵四边形ABCD是矩形,
(平行四边形的对角线互相平分),
∴AC=BD(矩形的对角线相等).
∴AO=BO.
∵∠1=120°,
∴∠2=60°.
∴△ABO是等边三角形.
∵AB=4cm,
∴OA=OB=4cm.
矩形的对角线有什么特征?
还能知道哪个角的度数?
那么△AOB是什么三角形?
等边
三角形
∴AC=BD=8cm.
AC=BD,
OA=OC,OB=OD.
矩形的两条对角线把矩形分成四个______的三角形.
等腰
如果两条对角线的夹角为60°,那么60°角所在的两个等腰三角形是_______三角形.
等边
1、根据图形求出相应的x、y的值(第1、3个图是矩形,第2个图是菱形;第3个图中的2x、2y+4、x+3y分别表示矩形对角线一半的长):
以上3题都是将几何问题转化为代数问题来解决的.
2、下列命题中假命题是( )
(A)矩形的对角线互相平分且相等;
(B)菱形的对角线互相平分且垂直;
(C)矩形的两条对角线把矩形分成四个直角三角形;
(D)菱形的两条对角线把菱形分成四个直角三角形;
C
3、利用矩形的性质,证明:直角三角形斜边上的中线等于斜边的一半.
已知:在Rt△ABC中,∠ACB=90°点D是斜边AB的中点.
求证:
E
证明:延长CD到点E,使得DE=CD,联结AE、BE.
∵点D是斜边AB的中点,
∴四边形ACBE是平行四边形
(对角线互相平分的四边形是平行四边形).
又∵ ∠ACB=90°,
∴四边形ACBE是矩形(有一个角是直角的平行四边形是矩形).
∴AB=CE(矩形的对角线相等).
∴
1、矩形、菱形的定义
有一个角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
2、矩形、菱形的性质
角
边
对角线
对称性
矩形
菱形
对边平行且相等
对角相等
对角线互相平分且相等.
对角线互相平分且互相垂直,每一条对角线平分一组对角.
中心对称图形
中心对称图形
每个角都
是直角
轴对称图形
四条边都相等
轴对称图形
对边平行
