沪教版(上海)数学七年级第二学期-14.5 等腰三角形复习 课件(共16张ppt)
文档属性
| 名称 | 沪教版(上海)数学七年级第二学期-14.5 等腰三角形复习 课件(共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 430.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 00:00:00 | ||
图片预览






文档简介
等腰三角形复习
一、顶角与底角的不确定
1.若等腰三角形的顶角是50°,则其它两个角的度数是 .
2.若等腰三角形的底角是50°,则其它两个角的度数是 .
3.若等腰三角形的一个内角是50°,则其它两个角的度数是 .
4.若等腰三角形的一个内角是130°,则其它两个角的度数是 .
变式: 在等腰△ABC中,∠B=50°,则
∠C= .
65°,65°
50°,80°
65°,65°或50°,80°
25°, 25°
50°或65°或80°
一、顶角与底角的不确定
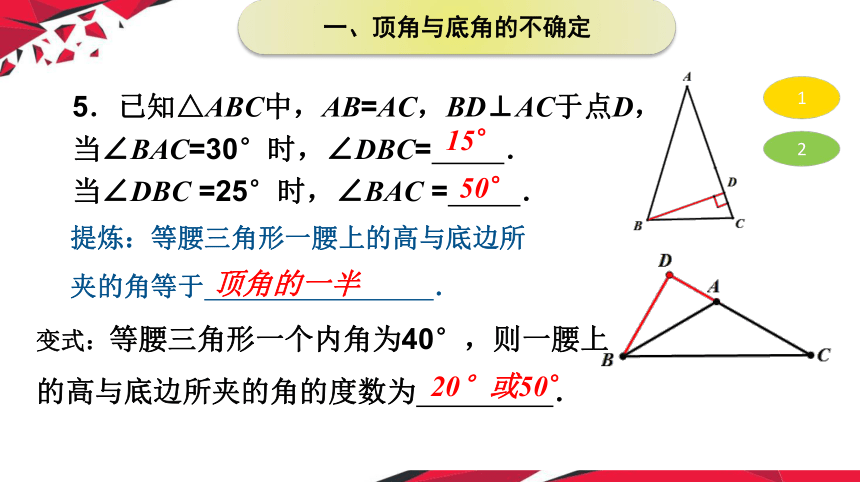
5.已知△ABC中,AB=AC,BD⊥AC于点D,
当∠BAC=30°时,∠DBC= .
当∠DBC =25°时,∠BAC = .
提炼:等腰三角形一腰上的高与底边所夹的角等于 .
1
2
15°
50°
顶角的一半
变式:等腰三角形一个内角为40°,则一腰上的高与底边所夹的角的度数为 .
20°或50°
一、顶角与底角的不确定
6.等腰三角形一腰上的高与另一腰的夹角为50°,则顶角为 .
提炼:等腰三角形一腰上的高与另一腰的夹角为 a,则顶角度数为 .
变式:等腰三角形一腰上的高与另一边的夹角为50°,则顶角为 .
40°或140°
90°- a或90°+ a
40°或100°或140°
一、顶角与底角的不确定
7.等腰三角形底边上的高与腰的夹角为50°,则底角为 .
提炼:等腰三角形底边上的高只能在三角形内.
等腰三角形一腰上的高可能在三角形内,可能在三角形外.(除等腰直角三角形)
40°
二、腰和底边的不确定
1.若等腰三角形的两边长为2和5,则这个等腰三角形的周长为 .
2.若等腰三角形的两边长为3和4,则这个等腰三角形的周长为 .
变式:若等腰三角形的周长为16,其中一边长为4,则底边长为 .
12
10或11
4
二、腰和底边的不确定
3.若等腰三角形的腰长是6,则底边长x的取值范围是 .
4.若等腰三角形的底边是6,则腰长y的取值范围是 .
5.若等腰三角形的周长是6,则腰长a的取值范围是 .
6.若等腰三角形的周长是6,则底边长b的取值范围是 .
变式:若等腰三角形周长12,边长都为整数,则等腰三角形
有 个.
0y>3
2
1.50三、方程思想在等腰三角形中的运用
1.如图,在△ABC中, 点D在边AC上,点E在边AB上,且AB=AC,BC=BD,AD=DE=EB,则∠A= .
2.如图,在△ABC中,AB=AC,BC=BD=ED=EA,则∠A= .
3.如图,在△ABC中,CA=CB,DF=DB,AE=AD,则∠A= .
45°
36°
三、方程思想在等腰三角形中的运用
4.如图,在△ABC中,点D在边BC上,且AB=DB,DA=DC,则∠BAC= .
5.如图,在△ABC中,点D在边BC上,且AD=DB=DC,则∠BAC= .
6.如图,在△ABC中,点D在边AC上,且AD=DB=DC,则∠BAC= .
108°
36°
90°
三、方程思想在等腰三角形中的运用
7.如图7,在△ABC中,点D在边AC上,且AD=DB,BC=DC,则∠BAC= .
提炼: 如果过等腰三角形的顶点画一条直线,将它分成两个等腰三角形,那么这个等腰三角形的顶角为 .
36°或90°或108°或
四、图形运动中的等腰三角形
1. 如图,将一块含有30°角的三角板△ABC绕着点A顺时针旋转90°后得到△AB′C′,则∠CC′B′的度数为 度.
2. 如图,将△ABC绕点C顺时针旋转40°得到△A′B′C,且AC⊥A′B′,则∠BAC= .
105
50°
四、图形运动中的等腰三角形
3. 如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转得△A′B′C,使点B′落在线段AB上,如果∠B=65°,则∠ACA′= .
4.如图:△ABC中,AB=AC,∠A=80°,将△ABC绕着点B顺时针旋转,使点A落在BC边上的点A′处,点C落在点C处,那么∠BCC′的度数是______.
50°
65°
四、图形运动中的等腰三角形
5. 如图5,在平面内将△ABC绕点A逆时针旋转至△AB′C′,使CC′∥AB,如果∠BAC=70°,那么旋转角a= 度.
6. 如图6,D是AB边上的中点,将沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则 ∠BDF= 度.
40
80
五、课堂小结
1、等腰三角形中的分类
2、图形运动中:对应边相等、对应角相等
3、等腰三角形一腰上的高与底边所夹的角等于顶角的一半
六、拓展思考
如图所示,已知Rt△ABC中,∠BCA=90°,∠BAC=30°,在直线BC或AC上取一点使△PAB是等腰三角形,则P点个数为 个.
6
7.如图,∠A=15°,AB=BC=CD=DE=EF,则∠FEM= .
典型问题选讲
7
8
8. 如图,AOB是一钢架,且∠AOB=10°,为加固钢架,需要在其内部添加一些钢管EF、FG、GH、…,添加的钢管长度都与OE相等,那么最多能添加这样钢管的根数为 .
一、顶角与底角的不确定
1.若等腰三角形的顶角是50°,则其它两个角的度数是 .
2.若等腰三角形的底角是50°,则其它两个角的度数是 .
3.若等腰三角形的一个内角是50°,则其它两个角的度数是 .
4.若等腰三角形的一个内角是130°,则其它两个角的度数是 .
变式: 在等腰△ABC中,∠B=50°,则
∠C= .
65°,65°
50°,80°
65°,65°或50°,80°
25°, 25°
50°或65°或80°
一、顶角与底角的不确定
5.已知△ABC中,AB=AC,BD⊥AC于点D,
当∠BAC=30°时,∠DBC= .
当∠DBC =25°时,∠BAC = .
提炼:等腰三角形一腰上的高与底边所夹的角等于 .
1
2
15°
50°
顶角的一半
变式:等腰三角形一个内角为40°,则一腰上的高与底边所夹的角的度数为 .
20°或50°
一、顶角与底角的不确定
6.等腰三角形一腰上的高与另一腰的夹角为50°,则顶角为 .
提炼:等腰三角形一腰上的高与另一腰的夹角为 a,则顶角度数为 .
变式:等腰三角形一腰上的高与另一边的夹角为50°,则顶角为 .
40°或140°
90°- a或90°+ a
40°或100°或140°
一、顶角与底角的不确定
7.等腰三角形底边上的高与腰的夹角为50°,则底角为 .
提炼:等腰三角形底边上的高只能在三角形内.
等腰三角形一腰上的高可能在三角形内,可能在三角形外.(除等腰直角三角形)
40°
二、腰和底边的不确定
1.若等腰三角形的两边长为2和5,则这个等腰三角形的周长为 .
2.若等腰三角形的两边长为3和4,则这个等腰三角形的周长为 .
变式:若等腰三角形的周长为16,其中一边长为4,则底边长为 .
12
10或11
4
二、腰和底边的不确定
3.若等腰三角形的腰长是6,则底边长x的取值范围是 .
4.若等腰三角形的底边是6,则腰长y的取值范围是 .
5.若等腰三角形的周长是6,则腰长a的取值范围是 .
6.若等腰三角形的周长是6,则底边长b的取值范围是 .
变式:若等腰三角形周长12,边长都为整数,则等腰三角形
有 个.
0
2
1.5
1.如图,在△ABC中, 点D在边AC上,点E在边AB上,且AB=AC,BC=BD,AD=DE=EB,则∠A= .
2.如图,在△ABC中,AB=AC,BC=BD=ED=EA,则∠A= .
3.如图,在△ABC中,CA=CB,DF=DB,AE=AD,则∠A= .
45°
36°
三、方程思想在等腰三角形中的运用
4.如图,在△ABC中,点D在边BC上,且AB=DB,DA=DC,则∠BAC= .
5.如图,在△ABC中,点D在边BC上,且AD=DB=DC,则∠BAC= .
6.如图,在△ABC中,点D在边AC上,且AD=DB=DC,则∠BAC= .
108°
36°
90°
三、方程思想在等腰三角形中的运用
7.如图7,在△ABC中,点D在边AC上,且AD=DB,BC=DC,则∠BAC= .
提炼: 如果过等腰三角形的顶点画一条直线,将它分成两个等腰三角形,那么这个等腰三角形的顶角为 .
36°或90°或108°或
四、图形运动中的等腰三角形
1. 如图,将一块含有30°角的三角板△ABC绕着点A顺时针旋转90°后得到△AB′C′,则∠CC′B′的度数为 度.
2. 如图,将△ABC绕点C顺时针旋转40°得到△A′B′C,且AC⊥A′B′,则∠BAC= .
105
50°
四、图形运动中的等腰三角形
3. 如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转得△A′B′C,使点B′落在线段AB上,如果∠B=65°,则∠ACA′= .
4.如图:△ABC中,AB=AC,∠A=80°,将△ABC绕着点B顺时针旋转,使点A落在BC边上的点A′处,点C落在点C处,那么∠BCC′的度数是______.
50°
65°
四、图形运动中的等腰三角形
5. 如图5,在平面内将△ABC绕点A逆时针旋转至△AB′C′,使CC′∥AB,如果∠BAC=70°,那么旋转角a= 度.
6. 如图6,D是AB边上的中点,将沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则 ∠BDF= 度.
40
80
五、课堂小结
1、等腰三角形中的分类
2、图形运动中:对应边相等、对应角相等
3、等腰三角形一腰上的高与底边所夹的角等于顶角的一半
六、拓展思考
如图所示,已知Rt△ABC中,∠BCA=90°,∠BAC=30°,在直线BC或AC上取一点使△PAB是等腰三角形,则P点个数为 个.
6
7.如图,∠A=15°,AB=BC=CD=DE=EF,则∠FEM= .
典型问题选讲
7
8
8. 如图,AOB是一钢架,且∠AOB=10°,为加固钢架,需要在其内部添加一些钢管EF、FG、GH、…,添加的钢管长度都与OE相等,那么最多能添加这样钢管的根数为 .
