沪教版(上海)数学七年级下册-12.1 实数的概念 课件(共29张ppt)
文档属性
| 名称 | 沪教版(上海)数学七年级下册-12.1 实数的概念 课件(共29张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 467.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 07:16:26 | ||
图片预览







文档简介
新学期!!
新气象!!
撸起袖子加油干!天上不会掉馅饼,实干才是硬道理!
§12.1实数的概念
复习引入
活动1
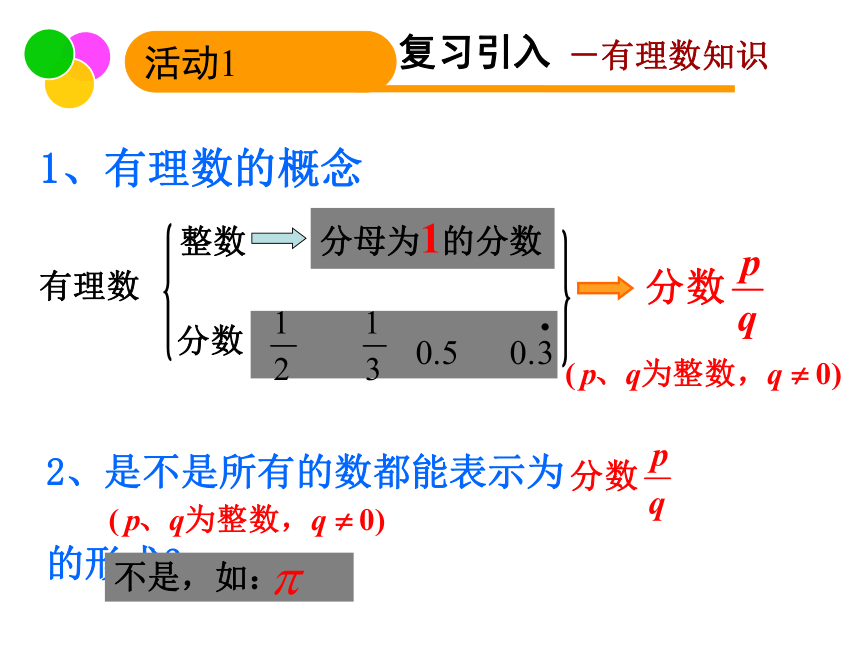
整数
分数
分母为1的分数
2、是不是所有的数都能表示为
的形式?
不是,如:
-有理数知识
有理数
1、有理数的概念
以生命为代价de发现
毕达哥拉斯(Pythagoras)学派
“万物皆为数”(指有理数)
希帕斯(Hippasus)
发现了一种实际存在的量,
却不能表示为两个整数的比
这意味着什么?
问题1 :面积为2的正方形存在吗?
探索新知
面积为1的正方形
面积为2的正方形
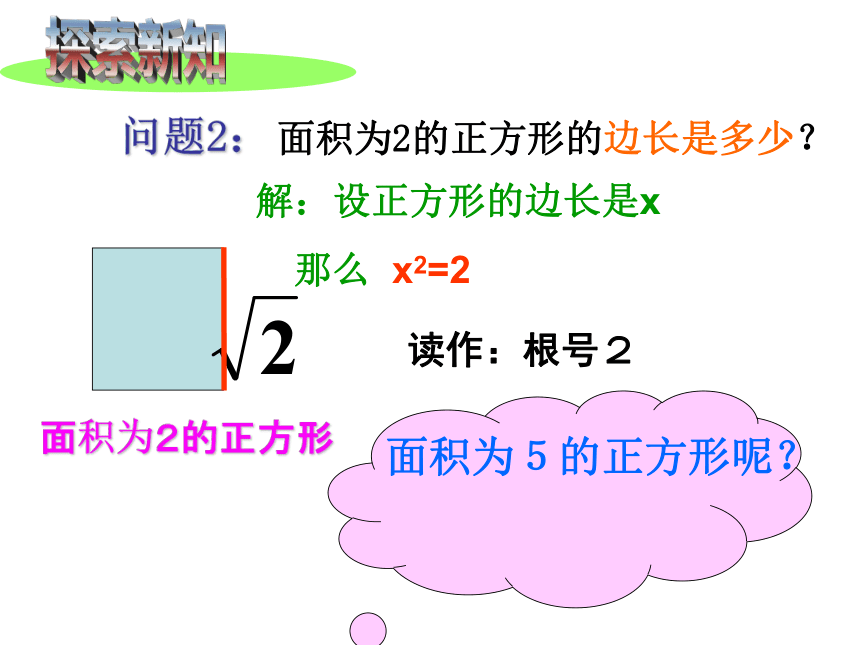
问题2: 面积为2的正方形的边长是多少?
探索新知
解:设正方形的边长是x
那么 x2=2
面积为2的正方形
读作:根号2
面积为5的正方形呢?
问题3 : 是个什么数?
探索新知
有理数
有限小数
无限循环小数
无限不循环小数
不是有理数
无限不循环小数称为无理数
无理数广泛存在着,一般有三种情况:
例如:
圆周率 及一些含有 的数都是无理数
第一种:
像 的数是无理数.
带根号的数都是无理数,这种说法对吗?
第二种:
有一定的规律,但不循环的无限小数都是无理数.
例如:
0.1010010001…〔两个1之间依次多1个0〕
234.232232223…〔两个3之间依次多1个2〕
0.12345678910111213 …〔小数部分有相继的正整数组成〕
第三种:
探究新知
1.无理数:无限不循环小数叫做无理数.
-无理数概念
正无理数
负无理数
无理数
2.无理数也有正负之分
3.只有符号不同的两个无理数互为相反数
有理数和无理数统称实数
实数范围内绝对值、相反数的意义和有理数范围内一样.
正有理数
有理数 零 ——有限小数或无限循环小数
实数 负有理数
正无理数
无理数 ——无限不循环小数
负无理数
实数的分类:
有理数和无理数统称为实数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
有限小数
无限循环小数
无理数
负无理数
正无理数
无限不循环小数
实数
实数范围内绝对值、相反数的意义和有理数范围内一样.
课堂练习
活动4
-及时巩固
(每相邻两个8之间, 1的个数从左到右依次递增且是无限小数)中,
无理数有 ,
正有理数有 ,
非负数有 ,
整数有 .
0
巩固练习:
1.将下列各数填入适当的括号内:
0、-3、 、6、3.14159、 、 、 、
π、0.3737737773….
有理数:﹛ ﹜;无理数:﹛ ﹜;
正实数:﹛ ﹜;负实数:﹛ ﹜;
非负数:﹛ ﹜;整 数:﹛ ﹜.
0.23、 、 、
例:将下列各数放入图中适当的位置:
0.101001000100001 、
、 4、 3.14、
有理数
无理数
整数
正整数
0.373373337……
4
0、
-2
0.101001000100001、
3.14、
0.373373337…
(它的位数无限
0、
-2、
、0.23
. .
. .
且相邻的两个3之间7的个数依次加1)
例题2 判断下列说法是否正确,并说明理由.
(1) 无限小数都是无理数;( )
×
无限循环小数
无限不循环小数
(分数)
(无理数)
(2) 无理数都是无限小数;( )
√
无限不循环小数
(3) 正实数包括正有理数和正无理数;( )
√
(4) 实数可以分为正实数和负实数两类.( )
×
还有0
例题2 判断下列说法是否正确,并说明理由.
×
×
(5) 实数a的倒数是
(6) 0是最小的实数,没有最大的实数.
(7) 两个无理数的和必是无理数.
×
(3) 正实数包括正有理数和正无理数;( )
√
(4) 实数可以分为正实数和负实数两类.( )
×
还有0
正无理数
正有理数
正实数
负无理数
负有理数
负实数
零
实数
练一练
1、试一试:把下面实数的分类图填写完整:
实数
整数
无理数
有理数
(无限不循环小数)
(q=1)
(q≠1)
分数
自然数
负整数
(p≥0)
(p<0)
(可表示成 的形式且p、q互素,q≠0)
练一练
2、你能写出在4和5之间的一个无理数吗?
你能写多少个?
练习
写出在2和3之间的一个无理数
课堂小结
1.无理数:无限不循环小数叫做无理数.
2.实数:有理数和无理数统称为实数.
正无理数
正有理数
正实数
负无理数
负有理数
负实数
零
实数
3.实数的分类.
有限小数
或无限循环小数
负有理数
有理数
负无理数
正无理数
无理数
无限不循环小数
零
实数
正有理数
如图所示,为16个边长为1的正方形拼成的面积为16的大正方形,请你在图中画出边长为根号8的正方形ABCD
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
正方形ABCD的边长为4,在AB,BC,CD,DA边上分别取点E、F、G、H,使得AE=BF=CG=DH=1,分别联结EF、FG、GH、HE.
(1)观察图形,四边形EFGH是怎样的四边形?
(2)求出四边形EFGH的边长.
1
1
1
1
3
3
3
3
小结
通过这节课的学习你有什么收获?
再见!
新气象!!
撸起袖子加油干!天上不会掉馅饼,实干才是硬道理!
§12.1实数的概念
复习引入
活动1
整数
分数
分母为1的分数
2、是不是所有的数都能表示为
的形式?
不是,如:
-有理数知识
有理数
1、有理数的概念
以生命为代价de发现
毕达哥拉斯(Pythagoras)学派
“万物皆为数”(指有理数)
希帕斯(Hippasus)
发现了一种实际存在的量,
却不能表示为两个整数的比
这意味着什么?
问题1 :面积为2的正方形存在吗?
探索新知
面积为1的正方形
面积为2的正方形
问题2: 面积为2的正方形的边长是多少?
探索新知
解:设正方形的边长是x
那么 x2=2
面积为2的正方形
读作:根号2
面积为5的正方形呢?
问题3 : 是个什么数?
探索新知
有理数
有限小数
无限循环小数
无限不循环小数
不是有理数
无限不循环小数称为无理数
无理数广泛存在着,一般有三种情况:
例如:
圆周率 及一些含有 的数都是无理数
第一种:
像 的数是无理数.
带根号的数都是无理数,这种说法对吗?
第二种:
有一定的规律,但不循环的无限小数都是无理数.
例如:
0.1010010001…〔两个1之间依次多1个0〕
234.232232223…〔两个3之间依次多1个2〕
0.12345678910111213 …〔小数部分有相继的正整数组成〕
第三种:
探究新知
1.无理数:无限不循环小数叫做无理数.
-无理数概念
正无理数
负无理数
无理数
2.无理数也有正负之分
3.只有符号不同的两个无理数互为相反数
有理数和无理数统称实数
实数范围内绝对值、相反数的意义和有理数范围内一样.
正有理数
有理数 零 ——有限小数或无限循环小数
实数 负有理数
正无理数
无理数 ——无限不循环小数
负无理数
实数的分类:
有理数和无理数统称为实数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
有限小数
无限循环小数
无理数
负无理数
正无理数
无限不循环小数
实数
实数范围内绝对值、相反数的意义和有理数范围内一样.
课堂练习
活动4
-及时巩固
(每相邻两个8之间, 1的个数从左到右依次递增且是无限小数)中,
无理数有 ,
正有理数有 ,
非负数有 ,
整数有 .
0
巩固练习:
1.将下列各数填入适当的括号内:
0、-3、 、6、3.14159、 、 、 、
π、0.3737737773….
有理数:﹛ ﹜;无理数:﹛ ﹜;
正实数:﹛ ﹜;负实数:﹛ ﹜;
非负数:﹛ ﹜;整 数:﹛ ﹜.
0.23、 、 、
例:将下列各数放入图中适当的位置:
0.101001000100001 、
、 4、 3.14、
有理数
无理数
整数
正整数
0.373373337……
4
0、
-2
0.101001000100001、
3.14、
0.373373337…
(它的位数无限
0、
-2、
、0.23
. .
. .
且相邻的两个3之间7的个数依次加1)
例题2 判断下列说法是否正确,并说明理由.
(1) 无限小数都是无理数;( )
×
无限循环小数
无限不循环小数
(分数)
(无理数)
(2) 无理数都是无限小数;( )
√
无限不循环小数
(3) 正实数包括正有理数和正无理数;( )
√
(4) 实数可以分为正实数和负实数两类.( )
×
还有0
例题2 判断下列说法是否正确,并说明理由.
×
×
(5) 实数a的倒数是
(6) 0是最小的实数,没有最大的实数.
(7) 两个无理数的和必是无理数.
×
(3) 正实数包括正有理数和正无理数;( )
√
(4) 实数可以分为正实数和负实数两类.( )
×
还有0
正无理数
正有理数
正实数
负无理数
负有理数
负实数
零
实数
练一练
1、试一试:把下面实数的分类图填写完整:
实数
整数
无理数
有理数
(无限不循环小数)
(q=1)
(q≠1)
分数
自然数
负整数
(p≥0)
(p<0)
(可表示成 的形式且p、q互素,q≠0)
练一练
2、你能写出在4和5之间的一个无理数吗?
你能写多少个?
练习
写出在2和3之间的一个无理数
课堂小结
1.无理数:无限不循环小数叫做无理数.
2.实数:有理数和无理数统称为实数.
正无理数
正有理数
正实数
负无理数
负有理数
负实数
零
实数
3.实数的分类.
有限小数
或无限循环小数
负有理数
有理数
负无理数
正无理数
无理数
无限不循环小数
零
实数
正有理数
如图所示,为16个边长为1的正方形拼成的面积为16的大正方形,请你在图中画出边长为根号8的正方形ABCD
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
正方形ABCD的边长为4,在AB,BC,CD,DA边上分别取点E、F、G、H,使得AE=BF=CG=DH=1,分别联结EF、FG、GH、HE.
(1)观察图形,四边形EFGH是怎样的四边形?
(2)求出四边形EFGH的边长.
1
1
1
1
3
3
3
3
小结
通过这节课的学习你有什么收获?
再见!
