沪教版(上海)数学七年级下册-13.5 (1)平行线的性质 课件(17张PPT)
文档属性
| 名称 | 沪教版(上海)数学七年级下册-13.5 (1)平行线的性质 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1009.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 20:35:19 | ||
图片预览





文档简介
13.5(1)平行线的性质
1
2
3
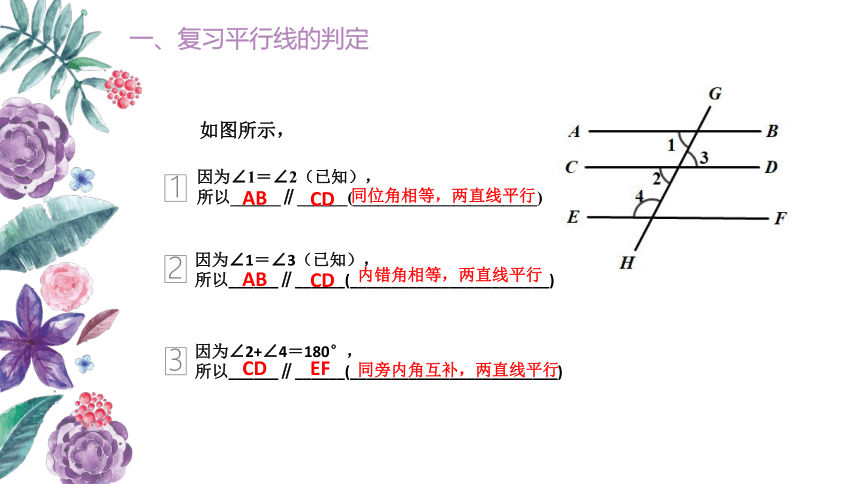
一、复习平行线的判定
如图所示,
因为∠1=∠2(已知),
所以______∥______(______________________)
因为∠1=∠3(已知),
所以______∥______(________________________)
因为∠2+∠4=180°,
所以______∥______(_________________________)
AB
CD
同位角相等,两直线平行
AB
CD
内错角相等,两直线平行
CD
EF
同旁内角互补,两直线平行
?
平行线的判定1:同位角相等, 两直线平行。
平行线的判定2:内错角相等, 两直线平行。
平行线的判定3:同旁内角互补,两直线平行。
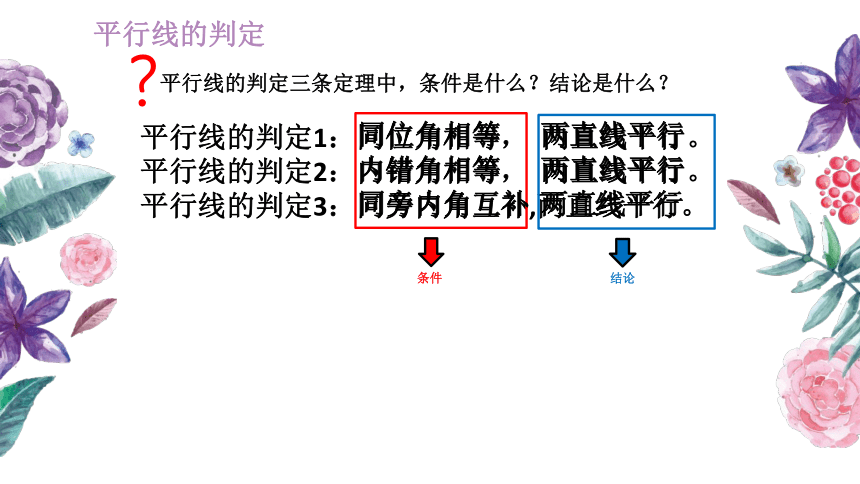
平行线的判定
平行线的判定三条定理中,条件是什么?结论是什么?
条件
两直线平行
两直线平行
两直线平行
同位角相等
内错角相等
同旁内角互补
结论
WHAT MAKES US
DIFFERENT?
85%
如图所示,已知直线a//b,且被直线c所截,请你说出图中各角的位置关系。
二、学习平行线的性质
∠1和∠3
∠1和∠2
∠1和∠4
∠3和∠4
∠2和∠3
∠2和∠4
对顶角
邻补角
邻补角
同位角
内错角
同旁内角
位置关系
数量关系
∠1=∠3
∠1+∠4=180°
∠3+∠4=180°
?
WHAT MAKES US
DIFFERENT?
85%
二、学习平行线的性质
在学习单上,画两条平行线a//b,一条截线c与这两条直线相交,得到同位角∠1与∠2,请利用身边的工具,探究它们的数量关系。
改变截线c的位置,再画一条截线c,探究∠1与∠2的数量关系是否任然相等,并和旁边同学交流下自己的结论。
如何用符号语言表示这个性质?
平行线性质1
两条平行线被第三条直线所截,同位角相等.
简单的说就是:两直线平行,同位角相等.
如果a//b,那么∠1=∠2
WHAT MAKES US
DIFFERENT?
85%
二、学习平行线的性质
如图,已知直线a//b,c为截线,能推出∠2与∠3的关系吗?为什么?
证明:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
∵ ∠1=∠3(对顶角相等)
∴∠2=∠3(等量代换)
平行线性质2
两条平行线被第三条直线所截,内错角相等.
简单的说就是:两直线平行,内错角相等.
如何用符号语言表示这个性质?
如果a//b,那么∠2=∠3
WHAT MAKES US
DIFFERENT?
85%
二、学习平行线的性质
如图:直线a、b被直线c所截,a∥b,∠4与∠2这对同旁内角有何数量关系?
证明:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
∵∠1+∠4=1800(邻补角的意义) ∠2+∠4=1800(等量代换)
证明:
∵a∥b(已知)
∴∠2=∠3(两直线平行,内错角相等)
∵∠3+∠4=1800(邻补角的意义) ∴∠4+∠2=1800(等量代换)
平行线性质3
两条平行线被第三条直线所截,同旁内角互补.
简单的说就是:两直线平行,同旁内角互补.
如何用符号语言表示这个性质?
如果a//b,那么∠2+∠4=180°
2
3
1
2
3
1
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。.
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
三、比较平行线判定和性质的区别
判定
性质
角之间的关系
平行
判定
性质
例1. 如图,已知直线AB、CD被直线AE所截,且AB∥CD
四、平行线性质的运用
(1)从∠1=115°,可以得到∠3是多少度?为什么?
解(1)
∵AB//CD(已知)
∴∠1=∠3(两直线平行,同位角相等)
∵∠1=115°(已知)
∴∠3=115°(等量代换)
例1. 如图,已知直线AB、CD被直线AE所截,且AB∥CD
四、平行线性质的运用
(1)从∠1=115°,可以得到∠3是多少度?为什么?
(2)从∠1=115°,可以得到∠2是多少度?为什么?
解(2)
∵AB//CD(已知)
∴∠1=∠2(两直线平行,内错角相等)
∵∠1=115°(已知)
∴∠2=115°(等量代换)
例1. 如图,已知直线AB、CD被直线AE所截,且AB∥CD
四、平行线性质的运用
(1)从∠1=115°,可以得到∠3是多少度?为什么?
(2)从∠1=115°,可以得到∠2是多少度?为什么?
(3)从∠1=115°,可以得到∠4是多少度?为什么?
解(3)
∵AB//CD(已知)
∴∠1+∠4=180°(两直线平行,同旁内角互补)
∵∠1=115°(已知)
∴∠4=180°-115°=65°(等量代换)
四、平行线性质的运用
例2.如图,已知直线AB//CD,AE//CM,∠A=39°,求∠C的度数。
变式:已知∠A=∠C,AB//CD,那么AE与CM平行吗?为什么?
3、平行线性质与判定的区别:
知道平行用性质;要证平行用判定。
4、要灵活运用平行线的性质与判定
1、平行线的性质定理:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补。
2、平行线性质的推导方法
用测量法和叠合法证明了平行线的性质1;
再利用性质1推导了性质2和3。
课堂小结
请同学谈谈自己收获与感想.
平行
角之间的关系
性质
判定
课后作业:
1、练习册、堂堂练13.5(1)、(2)
2、整理笔记
1
2
3
一、复习平行线的判定
如图所示,
因为∠1=∠2(已知),
所以______∥______(______________________)
因为∠1=∠3(已知),
所以______∥______(________________________)
因为∠2+∠4=180°,
所以______∥______(_________________________)
AB
CD
同位角相等,两直线平行
AB
CD
内错角相等,两直线平行
CD
EF
同旁内角互补,两直线平行
?
平行线的判定1:同位角相等, 两直线平行。
平行线的判定2:内错角相等, 两直线平行。
平行线的判定3:同旁内角互补,两直线平行。
平行线的判定
平行线的判定三条定理中,条件是什么?结论是什么?
条件
两直线平行
两直线平行
两直线平行
同位角相等
内错角相等
同旁内角互补
结论
WHAT MAKES US
DIFFERENT?
85%
如图所示,已知直线a//b,且被直线c所截,请你说出图中各角的位置关系。
二、学习平行线的性质
∠1和∠3
∠1和∠2
∠1和∠4
∠3和∠4
∠2和∠3
∠2和∠4
对顶角
邻补角
邻补角
同位角
内错角
同旁内角
位置关系
数量关系
∠1=∠3
∠1+∠4=180°
∠3+∠4=180°
?
WHAT MAKES US
DIFFERENT?
85%
二、学习平行线的性质
在学习单上,画两条平行线a//b,一条截线c与这两条直线相交,得到同位角∠1与∠2,请利用身边的工具,探究它们的数量关系。
改变截线c的位置,再画一条截线c,探究∠1与∠2的数量关系是否任然相等,并和旁边同学交流下自己的结论。
如何用符号语言表示这个性质?
平行线性质1
两条平行线被第三条直线所截,同位角相等.
简单的说就是:两直线平行,同位角相等.
如果a//b,那么∠1=∠2
WHAT MAKES US
DIFFERENT?
85%
二、学习平行线的性质
如图,已知直线a//b,c为截线,能推出∠2与∠3的关系吗?为什么?
证明:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
∵ ∠1=∠3(对顶角相等)
∴∠2=∠3(等量代换)
平行线性质2
两条平行线被第三条直线所截,内错角相等.
简单的说就是:两直线平行,内错角相等.
如何用符号语言表示这个性质?
如果a//b,那么∠2=∠3
WHAT MAKES US
DIFFERENT?
85%
二、学习平行线的性质
如图:直线a、b被直线c所截,a∥b,∠4与∠2这对同旁内角有何数量关系?
证明:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
∵∠1+∠4=1800(邻补角的意义) ∠2+∠4=1800(等量代换)
证明:
∵a∥b(已知)
∴∠2=∠3(两直线平行,内错角相等)
∵∠3+∠4=1800(邻补角的意义) ∴∠4+∠2=1800(等量代换)
平行线性质3
两条平行线被第三条直线所截,同旁内角互补.
简单的说就是:两直线平行,同旁内角互补.
如何用符号语言表示这个性质?
如果a//b,那么∠2+∠4=180°
2
3
1
2
3
1
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。.
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
三、比较平行线判定和性质的区别
判定
性质
角之间的关系
平行
判定
性质
例1. 如图,已知直线AB、CD被直线AE所截,且AB∥CD
四、平行线性质的运用
(1)从∠1=115°,可以得到∠3是多少度?为什么?
解(1)
∵AB//CD(已知)
∴∠1=∠3(两直线平行,同位角相等)
∵∠1=115°(已知)
∴∠3=115°(等量代换)
例1. 如图,已知直线AB、CD被直线AE所截,且AB∥CD
四、平行线性质的运用
(1)从∠1=115°,可以得到∠3是多少度?为什么?
(2)从∠1=115°,可以得到∠2是多少度?为什么?
解(2)
∵AB//CD(已知)
∴∠1=∠2(两直线平行,内错角相等)
∵∠1=115°(已知)
∴∠2=115°(等量代换)
例1. 如图,已知直线AB、CD被直线AE所截,且AB∥CD
四、平行线性质的运用
(1)从∠1=115°,可以得到∠3是多少度?为什么?
(2)从∠1=115°,可以得到∠2是多少度?为什么?
(3)从∠1=115°,可以得到∠4是多少度?为什么?
解(3)
∵AB//CD(已知)
∴∠1+∠4=180°(两直线平行,同旁内角互补)
∵∠1=115°(已知)
∴∠4=180°-115°=65°(等量代换)
四、平行线性质的运用
例2.如图,已知直线AB//CD,AE//CM,∠A=39°,求∠C的度数。
变式:已知∠A=∠C,AB//CD,那么AE与CM平行吗?为什么?
3、平行线性质与判定的区别:
知道平行用性质;要证平行用判定。
4、要灵活运用平行线的性质与判定
1、平行线的性质定理:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补。
2、平行线性质的推导方法
用测量法和叠合法证明了平行线的性质1;
再利用性质1推导了性质2和3。
课堂小结
请同学谈谈自己收获与感想.
平行
角之间的关系
性质
判定
课后作业:
1、练习册、堂堂练13.5(1)、(2)
2、整理笔记
