华东师大版2020年数学七年级上册第5章《5.2.2 平行线的判定》课件(共26张PPT)
文档属性
| 名称 | 华东师大版2020年数学七年级上册第5章《5.2.2 平行线的判定》课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 691.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 21:23:10 | ||
图片预览




文档简介
第5章 相交线与平行线
5.2 平行线
5.2.2 平行线的判定
华师版数学七年级上册
1.让学生理解并掌握平行线的四种判定方法;
2.让学生学会利用平行线的判定方法进行简单的推理;
3.培养学生严密的逻辑思维能力和推理能力.
学习目标
1.(1)如图,∠EDC与_______是同位角,它们是由直线DC和直线_____被直线______所截而成的;
(2)∠CDB与_______是内错角,它们是由直线____和直线____被直线____所截而成的;
(3)∠BCD与_______是同旁内角,它们是由直线____和直线____被直线_____所截而成的.
∠DAB
AB
AE
∠DBA
CD
AB
DB
∠ABC
CD
AB
CB
导入新知
2.要判定两条直线是否互相平行,我们无法依据它的定义来判断,要看这两条直线在无限延长的过程中是否永远不相交.那么从前面画平行线的过程中,我们可以得到什么启示吗?
知识模块一 平行线的判定方法1
阅读教材P171,完成下面的内容.
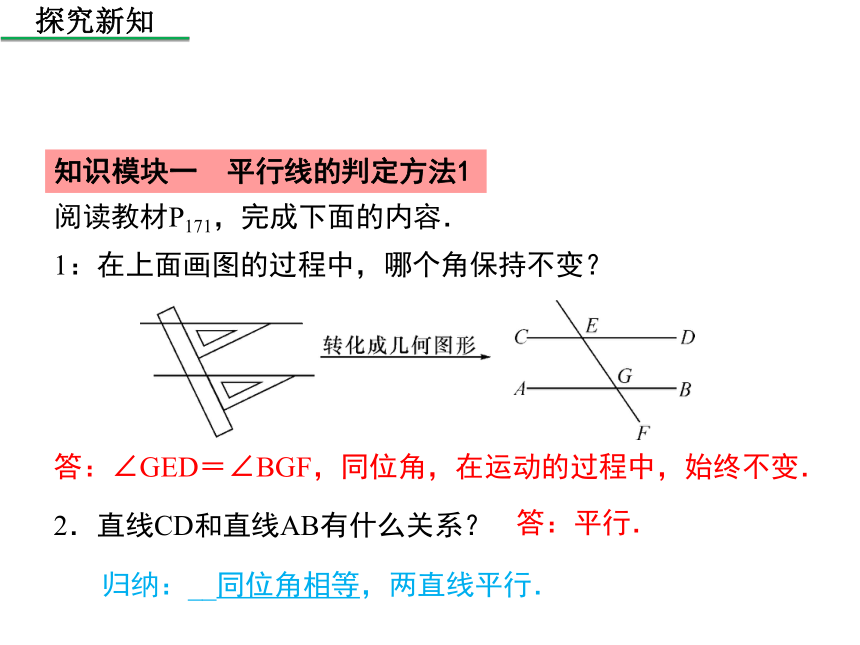
1:在上面画图的过程中,哪个角保持不变?
答:∠GED=∠BGF,同位角,在运动的过程中,始终不变.
2.直线CD和直线AB有什么关系?
答:平行.
归纳:__同位角相等,两直线平行.
探究新知
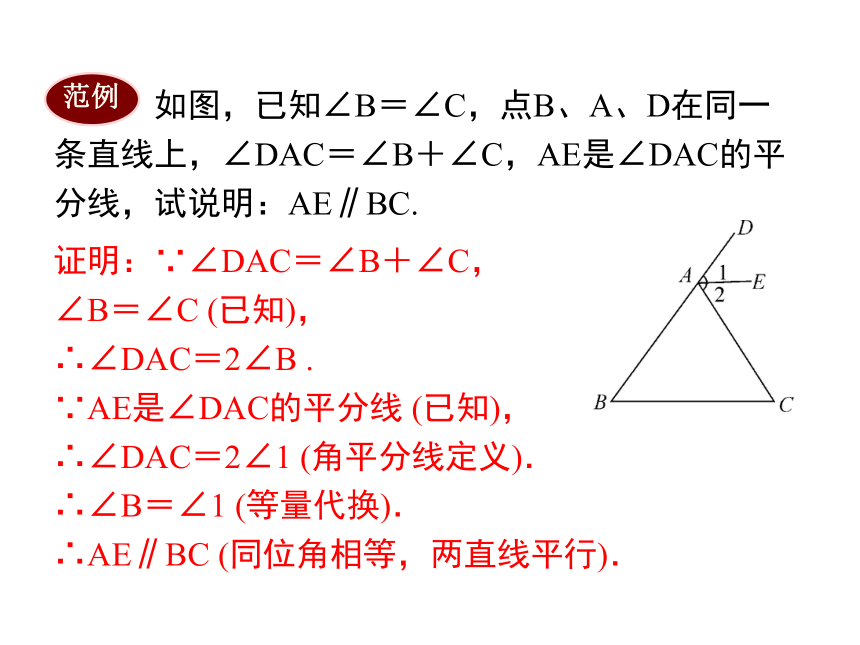
如图,已知∠B=∠C,点B、A、D在同一条直线上,∠DAC=∠B+∠C,AE是∠DAC的平分线,试说明:AE∥BC.
范例
证明:∵∠DAC=∠B+∠C,
∠B=∠C (已知),
∴∠DAC=2∠B .
∵AE是∠DAC的平分线 (已知),
∴∠DAC=2∠1 (角平分线定义).
∴∠B=∠1 (等量代换).
∴AE∥BC (同位角相等,两直线平行).
知识模块二 平行线的判定方法2
阅读教材P171例1,完成下面的内容.
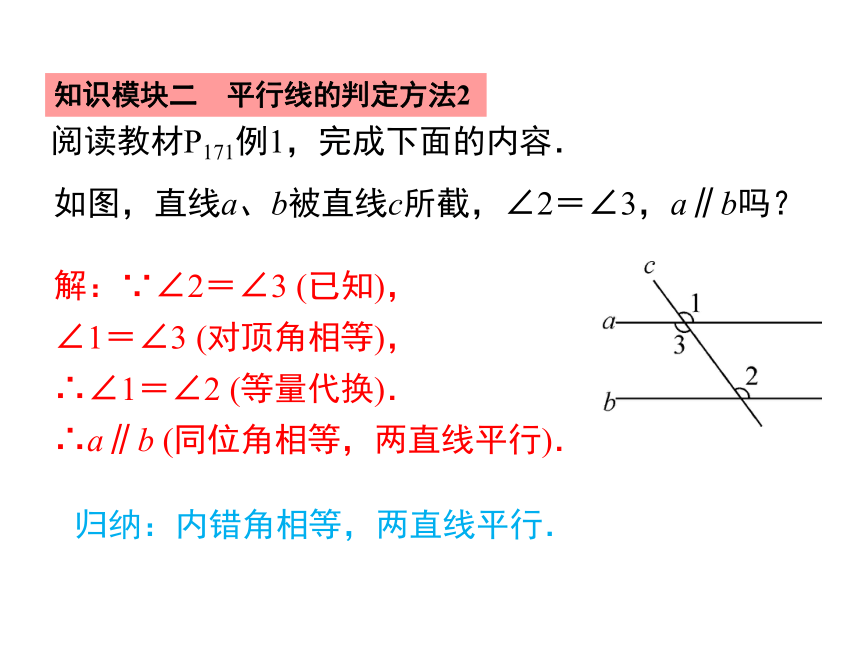
如图,直线a、b被直线c所截,∠2=∠3,a∥b吗?
解:∵∠2=∠3 (已知),
∠1=∠3 (对顶角相等),
∴∠1=∠2 (等量代换).
∴a∥b (同位角相等,两直线平行).
归纳:内错角相等,两直线平行.
知识模块三 平行线的判定方法3
阅读教材P173例2,完成下面的内容.
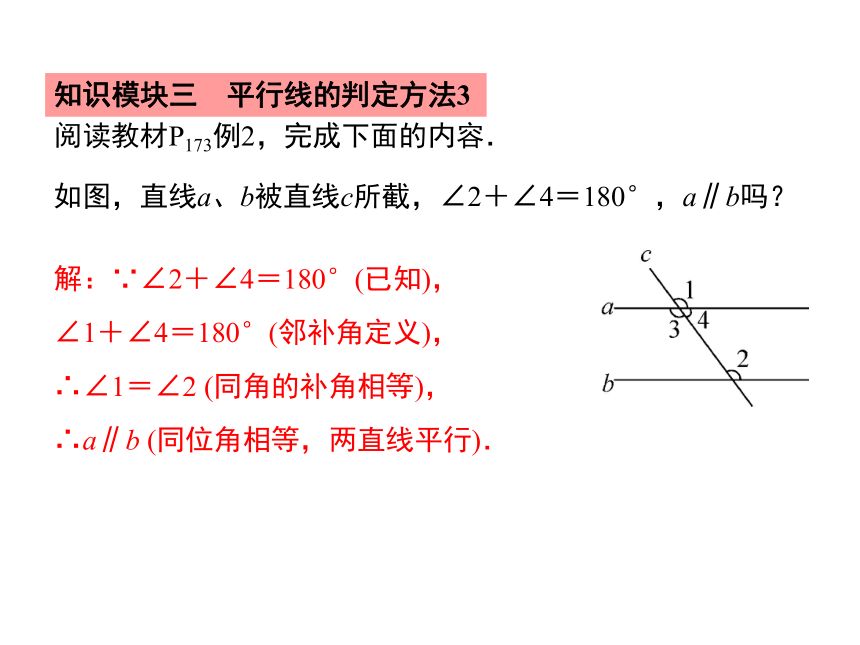
如图,直线a、b被直线c所截,∠2+∠4=180°,a∥b吗?
解:∵∠2+∠4=180°(已知),
∠1+∠4=180°(邻补角定义),
∴∠1=∠2 (同角的补角相等),
∴a∥b (同位角相等,两直线平行).
范例
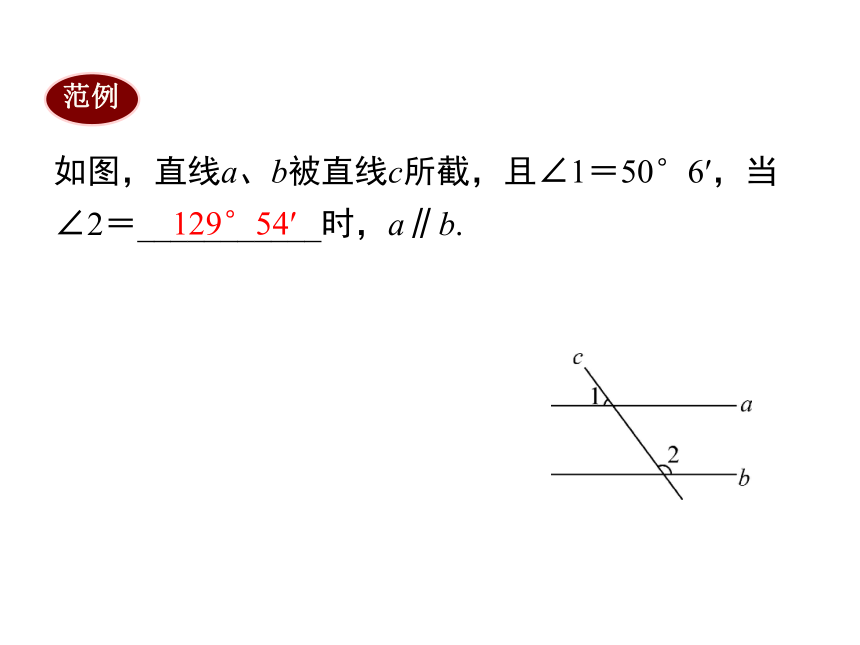
如图,直线a、b被直线c所截,且∠1=50°6′,当∠2=___________时,a∥b.
129°54′
知识模块四 平行线的判定方法4
阅读教材P173例3,完成下面的内容.
如图,在同一平面内,a⊥b,a⊥c,试说明b∥c.
证明:∵a⊥b,a⊥c (已知),
∴∠1=90°,∠2=90° (垂直定义).
∴∠1=∠2 (等量代换).
∴b∥c (内错角相等,两直线平行).
归纳:_________________________直线的两条直线平行.
在同一平面内,垂直于同一
范例
如图,CD⊥AB,请添加一个条件:_________,使得CD∥EF.
EF⊥AB
课堂练习
1.如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )
A.∠2=70° B.∠2=100°
C.∠2=110° D.∠3=110°
C
2.如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB∥BC B.BC∥CD
C.AB∥DC D.AB与CD相交
C
3.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,则a∥c
C
4.如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA
B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC
D.∠BAC=∠ACD
A
5.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是 ,
.
同位角相等
两直线平行
6.如图,∠1=60°,∠2=60°,则直线a与b的位置关系是 .
平行
7.如图,用几何语言表示下列句子.
(1)因为∠1和∠B相等,根据“同位角相等,两直线平行”,所以DE和BC平行;
(2)因为∠1和∠2相等,根据“内错角相等,两直线平行”,所以AB和EF平行;
(3)因为∠BDE和∠B互补,根据“同旁内角互补,两直线平行”,所以DE和BC平行.
解:(1)∵∠1=∠B(已知),
∴DE∥BC(同位角相等,两直线平行).
(2)∵∠1=∠2(已知),
∴EF∥AB(内错角相等,两直线平行).
(3)∵∠BDE+∠B=180°(已知),
∴DE∥BC(同旁内角互补,两直线平行).
8.如图,∠A+∠B+∠C+∠D=360°,且∠A=∠C,∠B=∠D,那么AB∥CD,AD∥BC.请说明理由.
解:∵∠A=∠C,∠B=∠D,
∴∠B+∠C=∠D+∠A
=360°÷2=180°.
∴AB∥CD.
∵∠A=∠C,∠B=∠D,
∴∠A+∠B=∠C+∠D=360°÷2=180°.
∴AD∥BC.
9.如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分∠APQ,QH平分∠DQP,并且∠1=∠2,说出图中哪些直线平行,并说明理由.
解:PG∥QH,AB∥CD.
∵PG平分∠APQ,QH平分∠DQP,
∴∠1=∠GPQ= ∠APQ,
∠PQH=∠2= ∠PQD.
又∵∠1=∠2,
∴∠GPQ=∠PQH,∠APQ=∠PQD.
∴PG∥QH,AB∥CD.
10.如图所示,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么?
解:CD∥EF.理由如下:
∵AB⊥BD,CD⊥BD,
∴AB∥CD.
∵∠1+∠2=180°,
∴AB∥EF.
∴CD∥EF.?
再 见
5.2 平行线
5.2.2 平行线的判定
华师版数学七年级上册
1.让学生理解并掌握平行线的四种判定方法;
2.让学生学会利用平行线的判定方法进行简单的推理;
3.培养学生严密的逻辑思维能力和推理能力.
学习目标
1.(1)如图,∠EDC与_______是同位角,它们是由直线DC和直线_____被直线______所截而成的;
(2)∠CDB与_______是内错角,它们是由直线____和直线____被直线____所截而成的;
(3)∠BCD与_______是同旁内角,它们是由直线____和直线____被直线_____所截而成的.
∠DAB
AB
AE
∠DBA
CD
AB
DB
∠ABC
CD
AB
CB
导入新知
2.要判定两条直线是否互相平行,我们无法依据它的定义来判断,要看这两条直线在无限延长的过程中是否永远不相交.那么从前面画平行线的过程中,我们可以得到什么启示吗?
知识模块一 平行线的判定方法1
阅读教材P171,完成下面的内容.
1:在上面画图的过程中,哪个角保持不变?
答:∠GED=∠BGF,同位角,在运动的过程中,始终不变.
2.直线CD和直线AB有什么关系?
答:平行.
归纳:__同位角相等,两直线平行.
探究新知
如图,已知∠B=∠C,点B、A、D在同一条直线上,∠DAC=∠B+∠C,AE是∠DAC的平分线,试说明:AE∥BC.
范例
证明:∵∠DAC=∠B+∠C,
∠B=∠C (已知),
∴∠DAC=2∠B .
∵AE是∠DAC的平分线 (已知),
∴∠DAC=2∠1 (角平分线定义).
∴∠B=∠1 (等量代换).
∴AE∥BC (同位角相等,两直线平行).
知识模块二 平行线的判定方法2
阅读教材P171例1,完成下面的内容.
如图,直线a、b被直线c所截,∠2=∠3,a∥b吗?
解:∵∠2=∠3 (已知),
∠1=∠3 (对顶角相等),
∴∠1=∠2 (等量代换).
∴a∥b (同位角相等,两直线平行).
归纳:内错角相等,两直线平行.
知识模块三 平行线的判定方法3
阅读教材P173例2,完成下面的内容.
如图,直线a、b被直线c所截,∠2+∠4=180°,a∥b吗?
解:∵∠2+∠4=180°(已知),
∠1+∠4=180°(邻补角定义),
∴∠1=∠2 (同角的补角相等),
∴a∥b (同位角相等,两直线平行).
范例
如图,直线a、b被直线c所截,且∠1=50°6′,当∠2=___________时,a∥b.
129°54′
知识模块四 平行线的判定方法4
阅读教材P173例3,完成下面的内容.
如图,在同一平面内,a⊥b,a⊥c,试说明b∥c.
证明:∵a⊥b,a⊥c (已知),
∴∠1=90°,∠2=90° (垂直定义).
∴∠1=∠2 (等量代换).
∴b∥c (内错角相等,两直线平行).
归纳:_________________________直线的两条直线平行.
在同一平面内,垂直于同一
范例
如图,CD⊥AB,请添加一个条件:_________,使得CD∥EF.
EF⊥AB
课堂练习
1.如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )
A.∠2=70° B.∠2=100°
C.∠2=110° D.∠3=110°
C
2.如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB∥BC B.BC∥CD
C.AB∥DC D.AB与CD相交
C
3.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,则a∥c
C
4.如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA
B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC
D.∠BAC=∠ACD
A
5.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是 ,
.
同位角相等
两直线平行
6.如图,∠1=60°,∠2=60°,则直线a与b的位置关系是 .
平行
7.如图,用几何语言表示下列句子.
(1)因为∠1和∠B相等,根据“同位角相等,两直线平行”,所以DE和BC平行;
(2)因为∠1和∠2相等,根据“内错角相等,两直线平行”,所以AB和EF平行;
(3)因为∠BDE和∠B互补,根据“同旁内角互补,两直线平行”,所以DE和BC平行.
解:(1)∵∠1=∠B(已知),
∴DE∥BC(同位角相等,两直线平行).
(2)∵∠1=∠2(已知),
∴EF∥AB(内错角相等,两直线平行).
(3)∵∠BDE+∠B=180°(已知),
∴DE∥BC(同旁内角互补,两直线平行).
8.如图,∠A+∠B+∠C+∠D=360°,且∠A=∠C,∠B=∠D,那么AB∥CD,AD∥BC.请说明理由.
解:∵∠A=∠C,∠B=∠D,
∴∠B+∠C=∠D+∠A
=360°÷2=180°.
∴AB∥CD.
∵∠A=∠C,∠B=∠D,
∴∠A+∠B=∠C+∠D=360°÷2=180°.
∴AD∥BC.
9.如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分∠APQ,QH平分∠DQP,并且∠1=∠2,说出图中哪些直线平行,并说明理由.
解:PG∥QH,AB∥CD.
∵PG平分∠APQ,QH平分∠DQP,
∴∠1=∠GPQ= ∠APQ,
∠PQH=∠2= ∠PQD.
又∵∠1=∠2,
∴∠GPQ=∠PQH,∠APQ=∠PQD.
∴PG∥QH,AB∥CD.
10.如图所示,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么?
解:CD∥EF.理由如下:
∵AB⊥BD,CD⊥BD,
∴AB∥CD.
∵∠1+∠2=180°,
∴AB∥EF.
∴CD∥EF.?
再 见
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
