人教版九年级数学下册课件-28.1 锐角三角函数3(18张)
文档属性
| 名称 | 人教版九年级数学下册课件-28.1 锐角三角函数3(18张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 273.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 01:09:51 | ||
图片预览





文档简介
课题:28.1 锐角三角函数
难点名称:特殊锐角的三角函数值及其运算
九年级-下册-第28章
目录
CONTENTS
导入
锐角三角函数的定义
在 中,
∠A的正弦:
∠A的余弦 :
探究学习
用数学视觉观察世界
用数学思维思考世界
?
思
考
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30°
60°
45°
45°
∴
30°
60°
探究学习
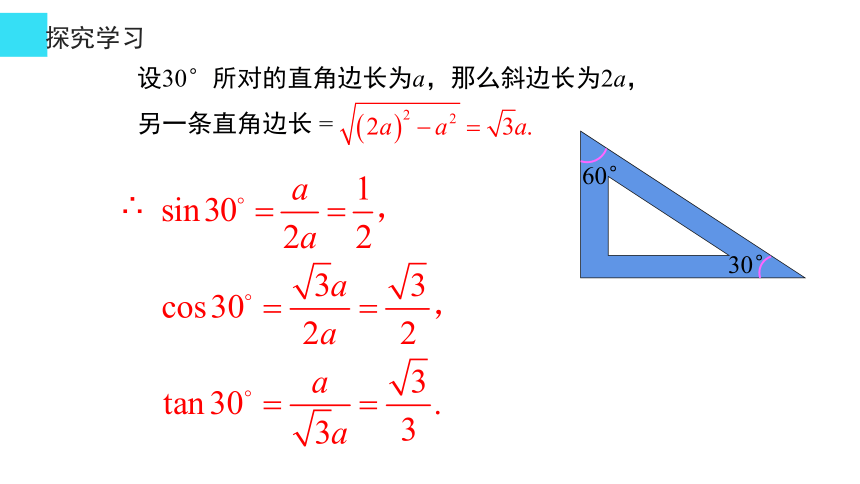
设30°所对的直角边长为a,那么斜边长为2a,
另一条直角边长 =
∴
30°
60°
探究学习
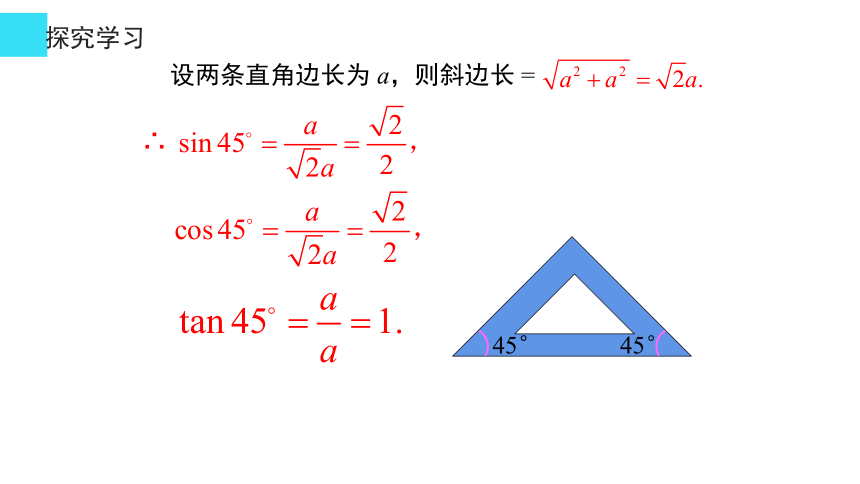
设两条直角边长为 a,则斜边长 =
∴
45°
45°
探究学习
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角
函数
30°
45°
60°
sin a
cos a
tan a
归纳:
1
仔细观察,说说你发现这张表有哪些规律?
1. 对于sinα与tanα,角度越大,函数值越 ;
对于cosα,角度越大,函数值越 .
2. 互余的两角之间的三角函数关系:
若∠A+∠B=90°,则sinA cosB,cosA sinB,
tanA · tanB = .
大
小
=
=
1
新发现
例1 求下列各式的值:
提示:cos260°表示(cos60°)2,即
(cos60°)×(cos60°).
解:cos260°+sin260°
典例精析
(1) cos260°+sin260°;
把60°改成30°再试试,你有什么猜想吗?
猜想:
可以尝试证明呦!
(2)
解:
典例精析
计算:
(1) sin30°+ cos45°;
解:原式 =
(2) sin230°+ cos230°-tan45°.
解:原式 =
课堂练习
课堂练习
求下列各式的值:
(3) 1-2 sin30°cos30°;
(4) 3tan30°-tan45°+2sin60°;
(5) ;
答案:(3)
(4)
(5) 2
再试试:
锐角度数与三角函数值间的转化:
三角函数值
锐角度数
转化
求适合下列各式的锐角α
再提升
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数
30°
45°
60°
sin a
cos a
tan a
对于sinα与tanα,角度越大,函数值也越大;
对于cosα,角度越大,函数值越小。
小结
谢谢!再见!
难点名称:特殊锐角的三角函数值及其运算
九年级-下册-第28章
目录
CONTENTS
导入
锐角三角函数的定义
在 中,
∠A的正弦:
∠A的余弦 :
探究学习
用数学视觉观察世界
用数学思维思考世界
?
思
考
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30°
60°
45°
45°
∴
30°
60°
探究学习
设30°所对的直角边长为a,那么斜边长为2a,
另一条直角边长 =
∴
30°
60°
探究学习
设两条直角边长为 a,则斜边长 =
∴
45°
45°
探究学习
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角
函数
30°
45°
60°
sin a
cos a
tan a
归纳:
1
仔细观察,说说你发现这张表有哪些规律?
1. 对于sinα与tanα,角度越大,函数值越 ;
对于cosα,角度越大,函数值越 .
2. 互余的两角之间的三角函数关系:
若∠A+∠B=90°,则sinA cosB,cosA sinB,
tanA · tanB = .
大
小
=
=
1
新发现
例1 求下列各式的值:
提示:cos260°表示(cos60°)2,即
(cos60°)×(cos60°).
解:cos260°+sin260°
典例精析
(1) cos260°+sin260°;
把60°改成30°再试试,你有什么猜想吗?
猜想:
可以尝试证明呦!
(2)
解:
典例精析
计算:
(1) sin30°+ cos45°;
解:原式 =
(2) sin230°+ cos230°-tan45°.
解:原式 =
课堂练习
课堂练习
求下列各式的值:
(3) 1-2 sin30°cos30°;
(4) 3tan30°-tan45°+2sin60°;
(5) ;
答案:(3)
(4)
(5) 2
再试试:
锐角度数与三角函数值间的转化:
三角函数值
锐角度数
转化
求适合下列各式的锐角α
再提升
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数
30°
45°
60°
sin a
cos a
tan a
对于sinα与tanα,角度越大,函数值也越大;
对于cosα,角度越大,函数值越小。
小结
谢谢!再见!
