人教版数学九年级上册22.1.2二次函数 课件(16张)
文档属性
| 名称 | 人教版数学九年级上册22.1.2二次函数 课件(16张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 01:10:16 | ||
图片预览






文档简介
22.1.2 二次函数y=ax2 的图象和性质
创设情境,导入新课
(2)你们知道:投篮时,篮球运动的路线是什么曲线?怎样计算篮球达到最高点时的高度?
(1)你们喜欢打篮球吗?
问题:
3(1)正比例函数y=kx(k≠0)的图像是______
(2)一次函数y=kx+b(k≠0)的图像是________
回顾:
1、画函数图像的一般步骤是什么?
2、二次函数的一般形式是怎样的?特殊形式呢?
思考:二次函数的图像是________
1.列表:
2.描点:
3.连线:
x
y=2x2
-2
0
1
-1
2
y=x2
y= x2
1
2
…
…
顶点坐标
1.画出函数y=x2、y=2x2、y= x2的图象:
1
2
y=x2
y=2x2
y= x2
1
2
a>0,开口都向上;
对称轴都是y轴;
增减性相同
只是开口
大小不同
顶点都是原点(0,0)
探究
1.列表:
2.描点:
3.连线:
x
y=-2x2
-2
0
1
-1
2
y=-x2
y=- x2
1
2
…
…
顶点坐标
2.画出函数y=-x2、y=-2x2、y=- x2的图象:
1
2
y=-x2
y=-2x2
y=- x2
1
2
y=x2
y=2x2
y= x2
1
2
a < 0,开口都向下;
对称轴都是y轴;
增减性相同.
只是开口
大小不同
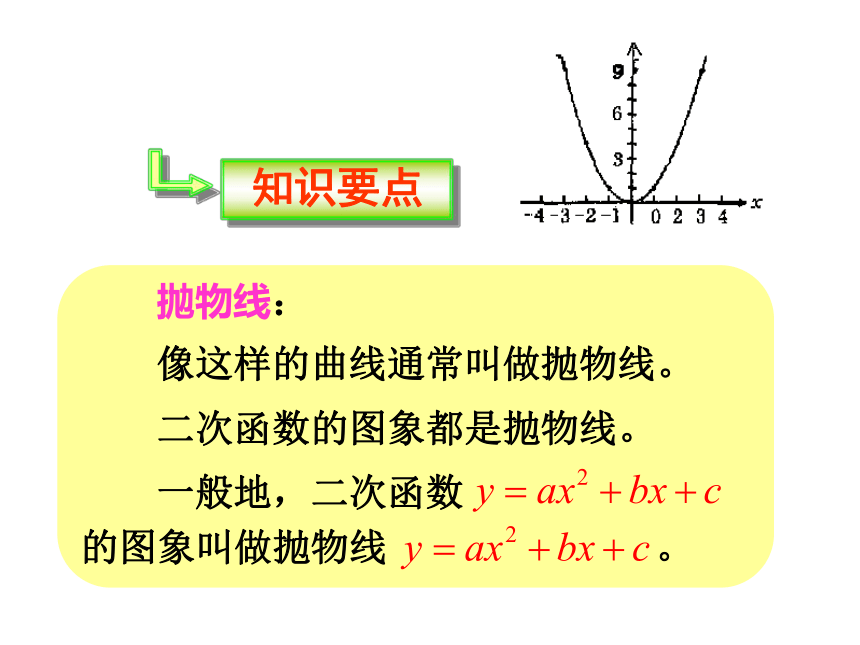
抛物线:
像这样的曲线通常叫做抛物线。
二次函数的图象都是抛物线。
一般地,二次函数 的图象叫做抛物线 。
知识要点
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y = x2
y = - x2
(0,0)
(0,0)
y轴
y轴
在x轴上方(除顶点外)
在x轴下方( 除顶点外)
向上
向下
当x=0时,y最小值=0
当x=0时,y最大值=0
当x<0时, y随着x的增大而减小.
当x>0时, y随着x的增大而增大.
当x<0时, y随着x的增大而增大.
当x>0时, y随着x的增大而减小.
y = x2、y= - x2
归纳:
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2 (a>0)
y= ax2 (a<0)
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,y最小值=0.
当x=0时,y最大值=0.
当x<0时,y随着x的增大而减小.
当x>o时, y随着x的增大而增大.
当x<0时,y随着x的增大而增大.
当x>0时, y随着x的增大而减小.
越小,开口越大.
越大,开口越小.
y = ax2
开口大小
归纳:
1、(1)抛物线 的开口方向_____,顶点____对称轴为____,当x___时,y随x的增大而减小;当x___时,y随x的增大而增大;当x___时,有最__值且为____
巩固练习
(2)类似方法,探讨抛物线 图像的性质
(3)二次函数 的图像共同点是________
2(1)函数 的图像如图所示,请指出三条抛物线的名称
(2)在同一坐标系中 这三个函数的图
像开口最大的是______最小的是_____开口向下的是______
题组一
3(1)函数 的图像之间有何关系?_____
(2)二次函数 开口大小,形状一样,开口方向相反,则a=______
巩固练习
(3)已知函数 经过点(1,2)①求a的值,
②当x<0时,y随x的变化情况
(4)已知抛物线的顶点在原点,对称轴是y轴,且经过点(-3,2)
求抛物线的解析式并指出x>0时,y随x的变化情况
题组一
1(1)在平面直角坐标系中,抛物线 与x轴的交点为___ 与y轴的交点为_____
巩固练习
题组二
(2)直线 与抛物线 的交点是______
2(1)二次函数 当 时,
(2)已知点(-2, ),(-1, ),(3, )都在函数
的图像上,则 之间大小关系为________
巩固练习
题组二
3(1)二次函数 与直线 图像交于点
P(1,m)
①求a,m的值. ②写出二次函数的表达式,并指出x取何值时,该表达式y随x的增大而增大?
(2)已知一次函数 的图像上有两点A, B ,它们
的横坐标分别是3,-1 若二次函数 的图像经过A,B 两点
①请求出一次函数的表达式 ②设二次函数的顶点为C,求?ABC的面积
课堂小结
形如 ________________(a、b、c是常数,a≠0)的函数叫做 x 的________,a叫做________________,b叫做_____________,c叫作________。
1. 二次函数:
2、抛物线:
二次函数的图象都是_________
抛物线
二次函数
二次项的系数
一次项的系数
常数项
一般地,抛物线 y=ax2 的对称轴是____轴,顶点是_______. 当a > 0时,抛物线的开口向__,顶点是抛物线的________,a 越大,抛物线的开口越___;当a < 0时,抛物线的开口向____,顶点是抛物线的最____点,a 越大,抛物线的开口越____.
y
原点
最低点
上
小
下
高
大
3、抛物线 y=ax2 的图象 :
4、抛物线 y=ax2 的图象 中 a 决定开口方向和形状。
a相同开口方向相同、形状相同,|a|越大,开口越小。
1、 T3,4 题
布置作业:
(2)把函数 的图像绕其顶点旋转180?,得到图像的解析式为______
2(1)若二次函数 的图像开口向下,则m=________
(3)已知函数 是关于x的二次函数
①求m的值
②当m为何值时,抛物线有最低点?最低点是什么?此时,当x在哪个范围内变化时,y随x的增大而增大?
③当m为何值时,函数有最大值?最大值是什么?此时,当x在哪个范围内变化时,y随x的增大而增大?
创设情境,导入新课
(2)你们知道:投篮时,篮球运动的路线是什么曲线?怎样计算篮球达到最高点时的高度?
(1)你们喜欢打篮球吗?
问题:
3(1)正比例函数y=kx(k≠0)的图像是______
(2)一次函数y=kx+b(k≠0)的图像是________
回顾:
1、画函数图像的一般步骤是什么?
2、二次函数的一般形式是怎样的?特殊形式呢?
思考:二次函数的图像是________
1.列表:
2.描点:
3.连线:
x
y=2x2
-2
0
1
-1
2
y=x2
y= x2
1
2
…
…
顶点坐标
1.画出函数y=x2、y=2x2、y= x2的图象:
1
2
y=x2
y=2x2
y= x2
1
2
a>0,开口都向上;
对称轴都是y轴;
增减性相同
只是开口
大小不同
顶点都是原点(0,0)
探究
1.列表:
2.描点:
3.连线:
x
y=-2x2
-2
0
1
-1
2
y=-x2
y=- x2
1
2
…
…
顶点坐标
2.画出函数y=-x2、y=-2x2、y=- x2的图象:
1
2
y=-x2
y=-2x2
y=- x2
1
2
y=x2
y=2x2
y= x2
1
2
a < 0,开口都向下;
对称轴都是y轴;
增减性相同.
只是开口
大小不同
抛物线:
像这样的曲线通常叫做抛物线。
二次函数的图象都是抛物线。
一般地,二次函数 的图象叫做抛物线 。
知识要点
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y = x2
y = - x2
(0,0)
(0,0)
y轴
y轴
在x轴上方(除顶点外)
在x轴下方( 除顶点外)
向上
向下
当x=0时,y最小值=0
当x=0时,y最大值=0
当x<0时, y随着x的增大而减小.
当x>0时, y随着x的增大而增大.
当x<0时, y随着x的增大而增大.
当x>0时, y随着x的增大而减小.
y = x2、y= - x2
归纳:
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2 (a>0)
y= ax2 (a<0)
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,y最小值=0.
当x=0时,y最大值=0.
当x<0时,y随着x的增大而减小.
当x>o时, y随着x的增大而增大.
当x<0时,y随着x的增大而增大.
当x>0时, y随着x的增大而减小.
越小,开口越大.
越大,开口越小.
y = ax2
开口大小
归纳:
1、(1)抛物线 的开口方向_____,顶点____对称轴为____,当x___时,y随x的增大而减小;当x___时,y随x的增大而增大;当x___时,有最__值且为____
巩固练习
(2)类似方法,探讨抛物线 图像的性质
(3)二次函数 的图像共同点是________
2(1)函数 的图像如图所示,请指出三条抛物线的名称
(2)在同一坐标系中 这三个函数的图
像开口最大的是______最小的是_____开口向下的是______
题组一
3(1)函数 的图像之间有何关系?_____
(2)二次函数 开口大小,形状一样,开口方向相反,则a=______
巩固练习
(3)已知函数 经过点(1,2)①求a的值,
②当x<0时,y随x的变化情况
(4)已知抛物线的顶点在原点,对称轴是y轴,且经过点(-3,2)
求抛物线的解析式并指出x>0时,y随x的变化情况
题组一
1(1)在平面直角坐标系中,抛物线 与x轴的交点为___ 与y轴的交点为_____
巩固练习
题组二
(2)直线 与抛物线 的交点是______
2(1)二次函数 当 时,
(2)已知点(-2, ),(-1, ),(3, )都在函数
的图像上,则 之间大小关系为________
巩固练习
题组二
3(1)二次函数 与直线 图像交于点
P(1,m)
①求a,m的值. ②写出二次函数的表达式,并指出x取何值时,该表达式y随x的增大而增大?
(2)已知一次函数 的图像上有两点A, B ,它们
的横坐标分别是3,-1 若二次函数 的图像经过A,B 两点
①请求出一次函数的表达式 ②设二次函数的顶点为C,求?ABC的面积
课堂小结
形如 ________________(a、b、c是常数,a≠0)的函数叫做 x 的________,a叫做________________,b叫做_____________,c叫作________。
1. 二次函数:
2、抛物线:
二次函数的图象都是_________
抛物线
二次函数
二次项的系数
一次项的系数
常数项
一般地,抛物线 y=ax2 的对称轴是____轴,顶点是_______. 当a > 0时,抛物线的开口向__,顶点是抛物线的________,a 越大,抛物线的开口越___;当a < 0时,抛物线的开口向____,顶点是抛物线的最____点,a 越大,抛物线的开口越____.
y
原点
最低点
上
小
下
高
大
3、抛物线 y=ax2 的图象 :
4、抛物线 y=ax2 的图象 中 a 决定开口方向和形状。
a相同开口方向相同、形状相同,|a|越大,开口越小。
1、 T3,4 题
布置作业:
(2)把函数 的图像绕其顶点旋转180?,得到图像的解析式为______
2(1)若二次函数 的图像开口向下,则m=________
(3)已知函数 是关于x的二次函数
①求m的值
②当m为何值时,抛物线有最低点?最低点是什么?此时,当x在哪个范围内变化时,y随x的增大而增大?
③当m为何值时,函数有最大值?最大值是什么?此时,当x在哪个范围内变化时,y随x的增大而增大?
同课章节目录
