人教版数学九年级上册22.1二次函数 课件(共29张ppt)
文档属性
| 名称 | 人教版数学九年级上册22.1二次函数 课件(共29张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 983.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 00:00:00 | ||
图片预览






文档简介
-2
2
2
4
6
4
-4
8
22.1 二次函数 (1)
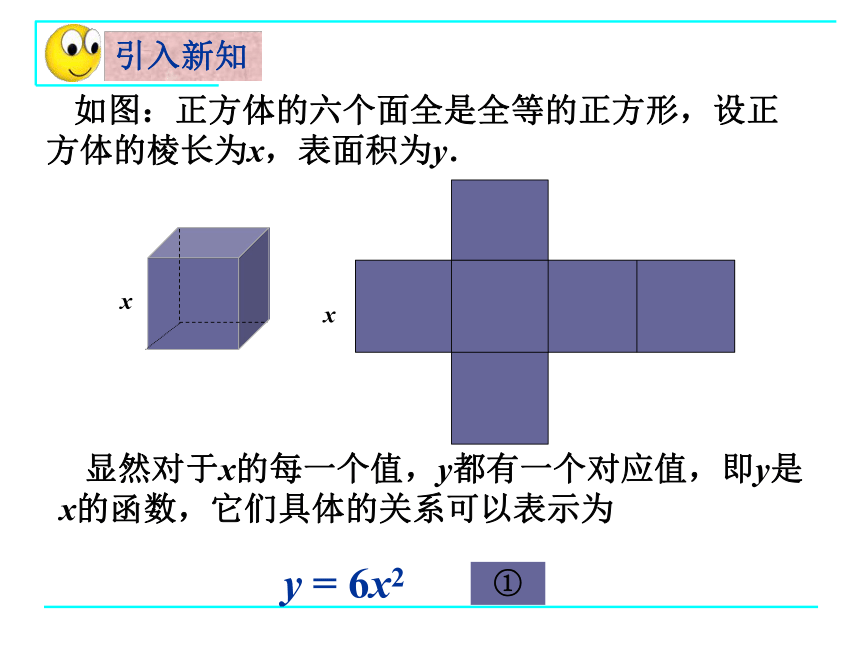
如图:正方体的六个面全是全等的正方形,设正方体的棱长为x,表面积为y.
y = 6x2
①
显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们具体的关系可以表示为
引入新知
x
x
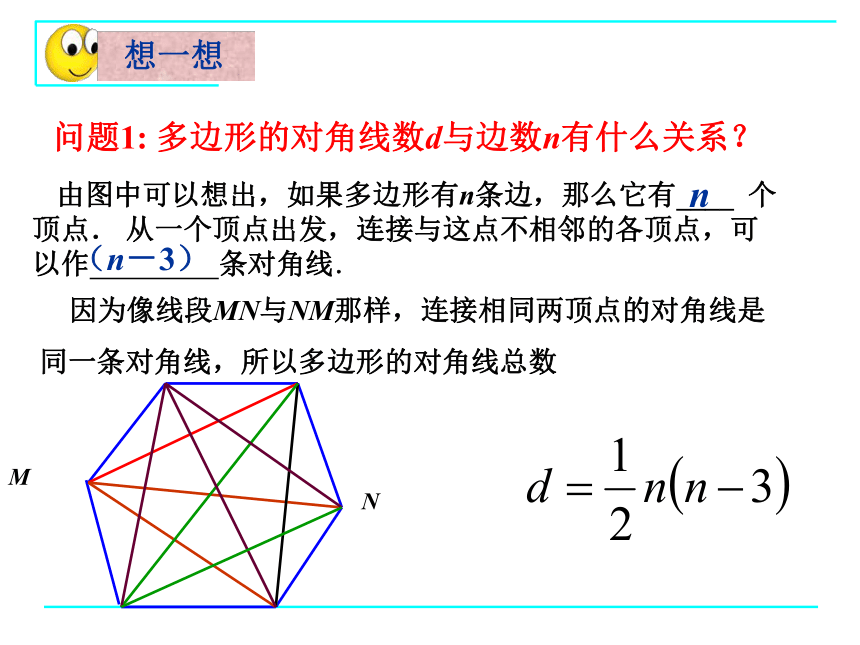
问题1: 多边形的对角线数d与边数n有什么关系?
由图中可以想出,如果多边形有n条边,那么它有____ 个顶点. 从一个顶点出发,连接与这点不相邻的各顶点,可以作 条对角线.
因为像线段MN与NM那样,连接相同两顶点的对角线是
同一条对角线,所以多边形的对角线总数
n
(n-3)
M
N
想一想
上式表示了多边形的对角线数d与边数n之间的关系,对于n的每一个值,d都有一个对应值,即d是n的函数.
即
②
想一想
问题2 :某工厂一种产品现在的年产量是20件,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
这种产品的原产量是20件,一年后的产量是 件,再经过一年后的产量是 件,即两年后的产量为
(20+20x)
(20+20x)+x(20+20x)
想一想
③式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
③
想一想
y = 6x2
①
③
②
有什么共同点?
函 数
在上面的问题中,函数都是用自变量的二次式表示的.
一般地,形如
的函数,叫做二次函数.其中,x是自变量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
细心观察
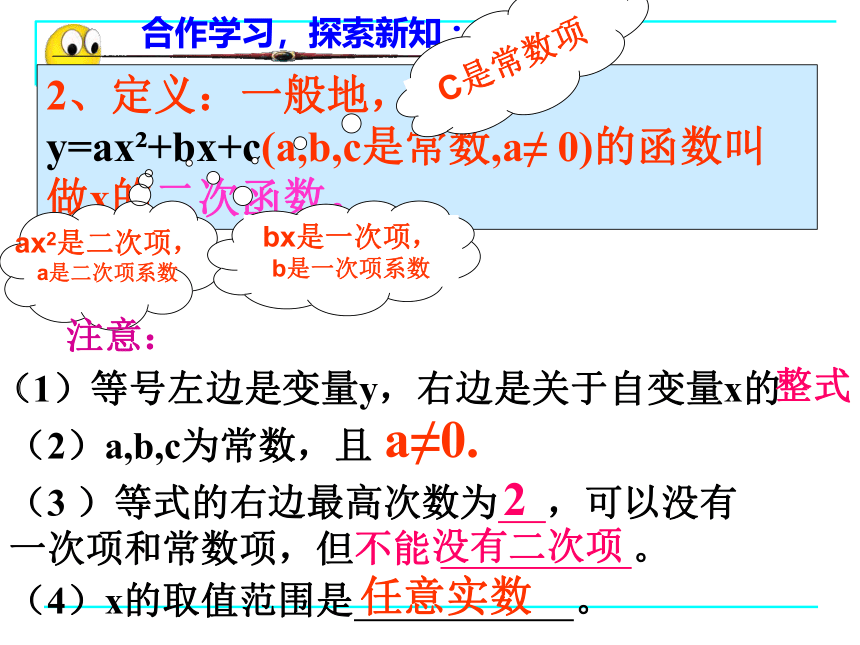
2、定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠ 0)的函数叫做x的二次函数。
(1)等号左边是变量y,右边是关于自变量x的
(3 )等式的右边最高次数为 ,可以没有一次项和常数项,但不能 。
(2)a,b,c为常数,且
(4)x的取值范围是 。
整式
a≠0.
2
任意实数
合作学习,探索新知 :
ax2是二次项,a是二次项系数
bx是一次项,
b是一次项系数
C是常数项
注意:
没有二次项
二次函数的一般形式:
y=ax2+bx+c (其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时, y=
当c=0时, y=
当b=0,c=0时, y=
ax2+c
ax2+bx
ax2
合作学习,探索新知 :
下列函数中,哪些是二次函数?
抓住机遇 展示自我
是
不是
是
不是
先化简后判断
下列函数 :
(1)y=3-2x2; (2)y= ;
(3)y=3x(2x-1) ; (4)y=-2 x2;
(5)y=x2-(3+x)2 ; (6)y=mx2+nx+p(其中m、n、p为常数)
其中是二次函数的是 (填序号).
(1)(3)(4)(6)
例1、下列函数中,哪些是二次函数?若是,分别指出二次项系数,一次项系数,常数项.
(1) y=3(x-1)?+1 (2) y=x+
(3) s=3-2t? (4) y=(x+3)?-x?
(5)y= -x (6) v=10π r?
1
x
__
x?
1
__
填空:
当a=0时,y= ,是 函数。
当a≠0,b=0时, y= ,是 函数。
当a≠0,b=0,c=0时,y= ,是 函数。
所以,当 时,
是二次函数。
bx+c
一次
ax2
二次
ax2+c
二次
a≠0
例1:已知 是关于x二次函数,
求 的取值范围。
练习:
①已知 是关于x的二次函数,求 的取值范围。
解:m-1≠0 所以 m ≠1
解:2m+1≠0 所以 m ≠-0.5
例2:已知 是关于x的二次函数,试
求 的值。
练习:
① 函数是关于x的二次函
数,求m的值.
m=±2
m2-7=2,m=±3,因为m≠3,所以m=-3
2
解: 由题意可得
注意:二次函数的二次项系数不能为零
1、下列函数中,(x是自变量),是二次函数的为( )
A y=ax2+bx+c B y2=x2-4x+1
C y=x2 D y=2+
2.函数 y=(m-n)x2+ mx+n 是二次函数的条件是( )
A m,n是常数,且m≠0 B m,n是常数,且n≠0
C m,n是常数,且m≠n D m,n为任何实数
B
C
——牛刀小试
例4:已知二次函数y=ax2,当x=3时,y= -5,当x= -5时,求y的值
练习:
(1)已知二次函数 y=ax2 +c ,当时x=2,y=4,当时x=-1,y=-3,求a,c 的值
(2)已知二次函数y=ax2+bx,当时x=1,y=-1,当时x=-1,y=7,求点(a,b)关于原点对称的点。
4. 已知二次函数y=x?+px+q,当x=1时,函数值为4,当x=2时,函数值为- 5, 求这个二次函数的解析式.
{
变量之间的关系
函数
一次函数
反比例函数
y=kx+b (k≠0)
正比例函数y=kx (k≠0)
y=k/x (k≠0)
二次函数
y=ax?+bx+c(a,b,c是常数,a≠ 0)
一元二次方程ax?+bx+c=0(a,b,c是常数,a≠ 0)
1.一个圆柱的高等于底面半径,写出它的表面积S与半径r之间的关系式.
2.n支球队参加比赛,每两队之间进行一场比赛.写出比赛的场次数m与球队数n之间的关系式.
r
r
每个球队都要跟(n-1)支球队进行比赛,因此要进行n(n-1)场比赛,由于甲队与乙队的比赛应是同一场比赛所以总比赛数目
课内练习
例3.写出下列各函数关系,写出自变量的取值范围,并判断它们是什么类型的函数.
(1)写出正方体的表面积S(cm2)与正方体棱长a(cm)之间的函数关系;
(2)写出圆的面积y(cm2)与它的周长x(cm)之间的函数关系;
(3)某种储蓄的年利率是1.98%,存入10000元本金,若不计利息,求本息和y(元)与所存年数x之间的函数关系;
(4)菱形的两条对角线的和为26cm,求菱形的面积S(cm2)与一对角线长x(cm)之间的函数关系.
例5:正方形铁片边长为15cm,在四个角上各剪去一个边长为x(cm)的小正方形,用余下的部分做成一个无盖的盒子.
(1)求盒子的表面积S(cm2)与小正方形边长x(cm)之间的函数关系式;
(2)当小正方形边长为3cm时,求盒子的表面积.
15
x
练习:
(1)在半径为5cm的圆面上从中挖去一个半径为xcm的圆面,剩下一个圆环的面积为ycm2,求y与x的函数关系式
(2)巳知矩形的周长为80cm,设它的一边为xcm,那么矩形的面积Scm2与x之间的函数关系式是什么?
3)如图26.1.2,一块草地是长为100m,宽为80m的矩形. 欲在中间修筑互相垂直且宽为xm的小路,若草坪面积为ym2,求y与x之间的函数关系式.
小
路
小 路
(4)某广告公司设计一幅周长为12m的矩形广告牌,广告设计费为每平方米1000元,设矩形一边长为xm,面积为Sm2.
① 求出S与x之间的函数关系式,并确定x的取值范围;
② 请你设计一个方案,使获得的设计费最多,并求出这个费用.
(5)某商场销售一批衬衫,平均每天可售出20件,每件赢利40元.,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施.经过市场调查发现,如果每件衬衫每降1元,商场平均每天可多售出2件.设每件衬衫降价x元,每天的利润为y元,
① 试写出y与x之间的函数关系式;
② 若商场平均每天赢利1200元,每件衬衫应降价多少元?
x
用20米的篱笆围一个矩形的花圃(如图),设连墙的一边为x,矩形的面积为y, 求:
(1)写出y关于x的函数关系式和
自变量的取值范围.
(2)当x=3时,矩形的面积为多少?
作业:
通过本节课的学习,你有哪些收获?
1、二次函数的定义;
2、表示简单变量之间的二次函数关系。
y=ax?+bx+c(a,b,c是常数,a≠ 0)
2
2
4
6
4
-4
8
22.1 二次函数 (1)
如图:正方体的六个面全是全等的正方形,设正方体的棱长为x,表面积为y.
y = 6x2
①
显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们具体的关系可以表示为
引入新知
x
x
问题1: 多边形的对角线数d与边数n有什么关系?
由图中可以想出,如果多边形有n条边,那么它有____ 个顶点. 从一个顶点出发,连接与这点不相邻的各顶点,可以作 条对角线.
因为像线段MN与NM那样,连接相同两顶点的对角线是
同一条对角线,所以多边形的对角线总数
n
(n-3)
M
N
想一想
上式表示了多边形的对角线数d与边数n之间的关系,对于n的每一个值,d都有一个对应值,即d是n的函数.
即
②
想一想
问题2 :某工厂一种产品现在的年产量是20件,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
这种产品的原产量是20件,一年后的产量是 件,再经过一年后的产量是 件,即两年后的产量为
(20+20x)
(20+20x)+x(20+20x)
想一想
③式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
③
想一想
y = 6x2
①
③
②
有什么共同点?
函 数
在上面的问题中,函数都是用自变量的二次式表示的.
一般地,形如
的函数,叫做二次函数.其中,x是自变量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
细心观察
2、定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠ 0)的函数叫做x的二次函数。
(1)等号左边是变量y,右边是关于自变量x的
(3 )等式的右边最高次数为 ,可以没有一次项和常数项,但不能 。
(2)a,b,c为常数,且
(4)x的取值范围是 。
整式
a≠0.
2
任意实数
合作学习,探索新知 :
ax2是二次项,a是二次项系数
bx是一次项,
b是一次项系数
C是常数项
注意:
没有二次项
二次函数的一般形式:
y=ax2+bx+c (其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时, y=
当c=0时, y=
当b=0,c=0时, y=
ax2+c
ax2+bx
ax2
合作学习,探索新知 :
下列函数中,哪些是二次函数?
抓住机遇 展示自我
是
不是
是
不是
先化简后判断
下列函数 :
(1)y=3-2x2; (2)y= ;
(3)y=3x(2x-1) ; (4)y=-2 x2;
(5)y=x2-(3+x)2 ; (6)y=mx2+nx+p(其中m、n、p为常数)
其中是二次函数的是 (填序号).
(1)(3)(4)(6)
例1、下列函数中,哪些是二次函数?若是,分别指出二次项系数,一次项系数,常数项.
(1) y=3(x-1)?+1 (2) y=x+
(3) s=3-2t? (4) y=(x+3)?-x?
(5)y= -x (6) v=10π r?
1
x
__
x?
1
__
填空:
当a=0时,y= ,是 函数。
当a≠0,b=0时, y= ,是 函数。
当a≠0,b=0,c=0时,y= ,是 函数。
所以,当 时,
是二次函数。
bx+c
一次
ax2
二次
ax2+c
二次
a≠0
例1:已知 是关于x二次函数,
求 的取值范围。
练习:
①已知 是关于x的二次函数,求 的取值范围。
解:m-1≠0 所以 m ≠1
解:2m+1≠0 所以 m ≠-0.5
例2:已知 是关于x的二次函数,试
求 的值。
练习:
① 函数是关于x的二次函
数,求m的值.
m=±2
m2-7=2,m=±3,因为m≠3,所以m=-3
2
解: 由题意可得
注意:二次函数的二次项系数不能为零
1、下列函数中,(x是自变量),是二次函数的为( )
A y=ax2+bx+c B y2=x2-4x+1
C y=x2 D y=2+
2.函数 y=(m-n)x2+ mx+n 是二次函数的条件是( )
A m,n是常数,且m≠0 B m,n是常数,且n≠0
C m,n是常数,且m≠n D m,n为任何实数
B
C
——牛刀小试
例4:已知二次函数y=ax2,当x=3时,y= -5,当x= -5时,求y的值
练习:
(1)已知二次函数 y=ax2 +c ,当时x=2,y=4,当时x=-1,y=-3,求a,c 的值
(2)已知二次函数y=ax2+bx,当时x=1,y=-1,当时x=-1,y=7,求点(a,b)关于原点对称的点。
4. 已知二次函数y=x?+px+q,当x=1时,函数值为4,当x=2时,函数值为- 5, 求这个二次函数的解析式.
{
变量之间的关系
函数
一次函数
反比例函数
y=kx+b (k≠0)
正比例函数y=kx (k≠0)
y=k/x (k≠0)
二次函数
y=ax?+bx+c(a,b,c是常数,a≠ 0)
一元二次方程ax?+bx+c=0(a,b,c是常数,a≠ 0)
1.一个圆柱的高等于底面半径,写出它的表面积S与半径r之间的关系式.
2.n支球队参加比赛,每两队之间进行一场比赛.写出比赛的场次数m与球队数n之间的关系式.
r
r
每个球队都要跟(n-1)支球队进行比赛,因此要进行n(n-1)场比赛,由于甲队与乙队的比赛应是同一场比赛所以总比赛数目
课内练习
例3.写出下列各函数关系,写出自变量的取值范围,并判断它们是什么类型的函数.
(1)写出正方体的表面积S(cm2)与正方体棱长a(cm)之间的函数关系;
(2)写出圆的面积y(cm2)与它的周长x(cm)之间的函数关系;
(3)某种储蓄的年利率是1.98%,存入10000元本金,若不计利息,求本息和y(元)与所存年数x之间的函数关系;
(4)菱形的两条对角线的和为26cm,求菱形的面积S(cm2)与一对角线长x(cm)之间的函数关系.
例5:正方形铁片边长为15cm,在四个角上各剪去一个边长为x(cm)的小正方形,用余下的部分做成一个无盖的盒子.
(1)求盒子的表面积S(cm2)与小正方形边长x(cm)之间的函数关系式;
(2)当小正方形边长为3cm时,求盒子的表面积.
15
x
练习:
(1)在半径为5cm的圆面上从中挖去一个半径为xcm的圆面,剩下一个圆环的面积为ycm2,求y与x的函数关系式
(2)巳知矩形的周长为80cm,设它的一边为xcm,那么矩形的面积Scm2与x之间的函数关系式是什么?
3)如图26.1.2,一块草地是长为100m,宽为80m的矩形. 欲在中间修筑互相垂直且宽为xm的小路,若草坪面积为ym2,求y与x之间的函数关系式.
小
路
小 路
(4)某广告公司设计一幅周长为12m的矩形广告牌,广告设计费为每平方米1000元,设矩形一边长为xm,面积为Sm2.
① 求出S与x之间的函数关系式,并确定x的取值范围;
② 请你设计一个方案,使获得的设计费最多,并求出这个费用.
(5)某商场销售一批衬衫,平均每天可售出20件,每件赢利40元.,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施.经过市场调查发现,如果每件衬衫每降1元,商场平均每天可多售出2件.设每件衬衫降价x元,每天的利润为y元,
① 试写出y与x之间的函数关系式;
② 若商场平均每天赢利1200元,每件衬衫应降价多少元?
x
用20米的篱笆围一个矩形的花圃(如图),设连墙的一边为x,矩形的面积为y, 求:
(1)写出y关于x的函数关系式和
自变量的取值范围.
(2)当x=3时,矩形的面积为多少?
作业:
通过本节课的学习,你有哪些收获?
1、二次函数的定义;
2、表示简单变量之间的二次函数关系。
y=ax?+bx+c(a,b,c是常数,a≠ 0)
同课章节目录
