人教版数学九年级上册第二十一章《21.1一元二次方程》课件(共19张PPT)
文档属性
| 名称 | 人教版数学九年级上册第二十一章《21.1一元二次方程》课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 21:18:27 | ||
图片预览






文档简介
人教版数学九年级上册
第二十一章 二元一次方程
21.1 一元二次方程
21.1 一元二次方程
一元二次方程
人教版-数学-九年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
1.探索一元二次方程及其相关概念,能够辨别各项系数;能够从实际问题中抽象出方程知识。
2.在探索问题的过程中感受方程是刻画现实世界的一个模型,体会方程与实际生活的联系。
3.培养良好的研究问题的习惯,逐步提高自己的数学素养。
4.通过用一元二次方程解决身边的问题,体会数学知识应用的价值,了解数学对促进社会进步和发展人类理性精神的作用。
学习目标
古算趣题:“笨人执竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭.有个邻居聪明者,教他斜竿对两角,笨伯依言试一试,不多不少刚抵足.借问竿长多少数,谁人算出我佩服.”若设竿长为x尺,则可列方程为________________.
?
导入新知
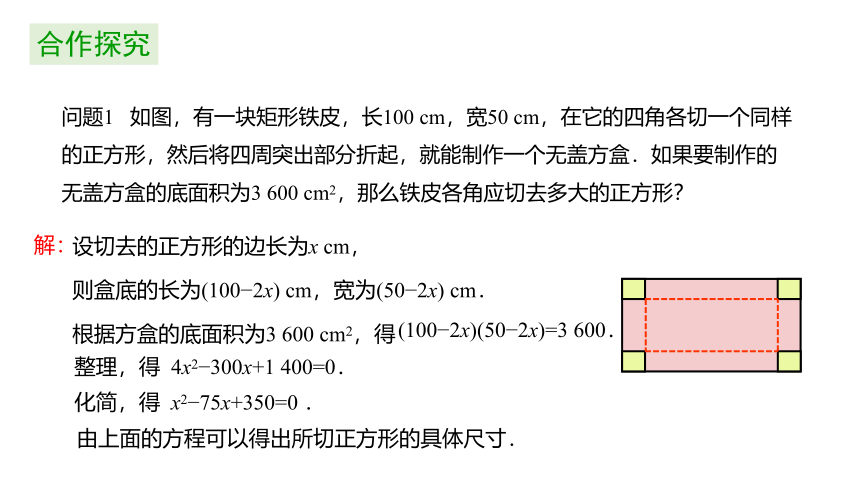
问题1 如图,有一块矩形铁皮,长100 cm,宽50 cm,在它的四角各切一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒.如果要制作的无盖方盒的底面积为3 600 cm2,那么铁皮各角应切去多大的正方形?
设切去的正方形的边长为x cm,
则盒底的长为(100?2x) cm,宽为(50?2x) cm.
根据方盒的底面积为3 600 cm2,得
(100?2x)(50?2x)=3 600.
整理,得 4x2?300x+1 400=0.
化简,得 x2?75x+350=0 .
由上面的方程可以得出所切正方形的具体尺寸.
解:
合作探究
问题2 要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛?
由上面的方程可以得出参赛队数.
全部比赛的场数为4×7=28.
?
?
化简,得x?? x=56 .
?
解:
1. 这些方程的两边都是整式;
2. 方程中只含有一个未知数,未知数的最高次数是2.
x2?x=56
x2?75x+350=0
x2+2x?4=0
观察由上面的问题得到的方程有什么特点?
等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程.
2.若方程 (m+2)x|m|?3mx+1=0 是关于x 的一元二次方程,则 ( )
A.m≠±2 B.m=2
C.m=?2 D.m=±2
?
B
B
典型例题
一般地,任何一个关于x的一元二次方程,经过整理,都能化成如下形式:ax?+bx+c=0 (a≠0)
这种形式叫做一元二次方程的一般形式 .
其中ax2是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项.
指出方程各项的系数时要带上前面的符号.
一元二次方程 ax2+bx+c=0(a≠0)中,为什么规定 a≠0? b,c可以为0吗?
合作探究
把下列方程化成一元二次方程的一般形式,并写出它们的二次项系数、一次项系数和常数项.
(1) ;
(2) ;
(3) .
1 -4 0
1 2 -14
2 -3 -9
典型例题
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根.
判断一个数值是不是一元二次方程的根的方法:
将这个值代入一元二次方程,看方程的左右两边是否相等,若相等,则是方程的根;若不相等,就不是方程的根.
合作探究
1. 下列哪些数是一元二次方程 x2-4x+3=0 的解?
-1, 0, 1, 3.
2. 方程 x2+x-12=0 的两个根为( )
A.x1=-2,x2=6 B.x1=-6,x2=2
C.x1=-3,x2=4 D.x1=-4,x2=3
D
典型例题
A.
B.5x2+y=0
C.ax2+bx+c=0
D.(x-1)(x+2)=1
D
1.下列选项中是一元二次方程的是( )
课堂练习
2.根据下列问题列方程,并将所列方程化成一元二次方程的一般形式:
(1)一个圆的面积是 6.28 cm2,求半径;
(2)一个直角三角形的两条直角边相差 3 cm,面积是 9 cm2,求较长的直角边.
?
3.如果 2 是方程 x2-c=0 的一个根,那么常数 c 是多少?求出这个方程的其他根.
解:因为 2 是方程 x2-c=0 的一个根,
所以 22-c=0,
解得 c=4,
则原方程为 x2-4=0,即x2=4,
因为 4 的平方根为±2,
所以方程 x2-4=0 的另一个根为-2.
解: 因为 a 为方程 x2-3x+1=0 的一根,
所以 a2-3a+1=0,
则a3-4a2+4a-1=a(a2-3a+1)-(a2-3a+1)=a×0-0=0.
4.已知 a 为方程 x2-3x+1=0 的一根,求 a3-4a2+4a-1 的值.
5.若 2n(n≠0) 是关于 x 的方程 x2-2mx+2n=0 的根,则 m-n 的值为 .
?
?
6.a是方程2x?=x+4的一个根,则代数式4a?-2a的值是 .
解:∵a是方程2x?=x+4的一个根,
∴2a?-a=4,
∴4a?-2a=2(2a?-a)=2×4=8.
8
7.如图,有一张矩形纸片,长10 cm,宽 6 cm,在它的四角各剪去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面面积是 32 cm2,求剪去的小正方形的边长.设剪去的小正方形的边长是 x cm,根据题意可列方程为( )
A.10×6-4×6x=32
B.(10-2x)(6-2x)=32
C.(10-x)(6-x)=32
D.10×6-4x2=32
B
再 见
第二十一章 二元一次方程
21.1 一元二次方程
21.1 一元二次方程
一元二次方程
人教版-数学-九年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
1.探索一元二次方程及其相关概念,能够辨别各项系数;能够从实际问题中抽象出方程知识。
2.在探索问题的过程中感受方程是刻画现实世界的一个模型,体会方程与实际生活的联系。
3.培养良好的研究问题的习惯,逐步提高自己的数学素养。
4.通过用一元二次方程解决身边的问题,体会数学知识应用的价值,了解数学对促进社会进步和发展人类理性精神的作用。
学习目标
古算趣题:“笨人执竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭.有个邻居聪明者,教他斜竿对两角,笨伯依言试一试,不多不少刚抵足.借问竿长多少数,谁人算出我佩服.”若设竿长为x尺,则可列方程为________________.
?
导入新知
问题1 如图,有一块矩形铁皮,长100 cm,宽50 cm,在它的四角各切一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒.如果要制作的无盖方盒的底面积为3 600 cm2,那么铁皮各角应切去多大的正方形?
设切去的正方形的边长为x cm,
则盒底的长为(100?2x) cm,宽为(50?2x) cm.
根据方盒的底面积为3 600 cm2,得
(100?2x)(50?2x)=3 600.
整理,得 4x2?300x+1 400=0.
化简,得 x2?75x+350=0 .
由上面的方程可以得出所切正方形的具体尺寸.
解:
合作探究
问题2 要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛?
由上面的方程可以得出参赛队数.
全部比赛的场数为4×7=28.
?
?
化简,得x?? x=56 .
?
解:
1. 这些方程的两边都是整式;
2. 方程中只含有一个未知数,未知数的最高次数是2.
x2?x=56
x2?75x+350=0
x2+2x?4=0
观察由上面的问题得到的方程有什么特点?
等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程.
2.若方程 (m+2)x|m|?3mx+1=0 是关于x 的一元二次方程,则 ( )
A.m≠±2 B.m=2
C.m=?2 D.m=±2
?
B
B
典型例题
一般地,任何一个关于x的一元二次方程,经过整理,都能化成如下形式:ax?+bx+c=0 (a≠0)
这种形式叫做一元二次方程的一般形式 .
其中ax2是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项.
指出方程各项的系数时要带上前面的符号.
一元二次方程 ax2+bx+c=0(a≠0)中,为什么规定 a≠0? b,c可以为0吗?
合作探究
把下列方程化成一元二次方程的一般形式,并写出它们的二次项系数、一次项系数和常数项.
(1) ;
(2) ;
(3) .
1 -4 0
1 2 -14
2 -3 -9
典型例题
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根.
判断一个数值是不是一元二次方程的根的方法:
将这个值代入一元二次方程,看方程的左右两边是否相等,若相等,则是方程的根;若不相等,就不是方程的根.
合作探究
1. 下列哪些数是一元二次方程 x2-4x+3=0 的解?
-1, 0, 1, 3.
2. 方程 x2+x-12=0 的两个根为( )
A.x1=-2,x2=6 B.x1=-6,x2=2
C.x1=-3,x2=4 D.x1=-4,x2=3
D
典型例题
A.
B.5x2+y=0
C.ax2+bx+c=0
D.(x-1)(x+2)=1
D
1.下列选项中是一元二次方程的是( )
课堂练习
2.根据下列问题列方程,并将所列方程化成一元二次方程的一般形式:
(1)一个圆的面积是 6.28 cm2,求半径;
(2)一个直角三角形的两条直角边相差 3 cm,面积是 9 cm2,求较长的直角边.
?
3.如果 2 是方程 x2-c=0 的一个根,那么常数 c 是多少?求出这个方程的其他根.
解:因为 2 是方程 x2-c=0 的一个根,
所以 22-c=0,
解得 c=4,
则原方程为 x2-4=0,即x2=4,
因为 4 的平方根为±2,
所以方程 x2-4=0 的另一个根为-2.
解: 因为 a 为方程 x2-3x+1=0 的一根,
所以 a2-3a+1=0,
则a3-4a2+4a-1=a(a2-3a+1)-(a2-3a+1)=a×0-0=0.
4.已知 a 为方程 x2-3x+1=0 的一根,求 a3-4a2+4a-1 的值.
5.若 2n(n≠0) 是关于 x 的方程 x2-2mx+2n=0 的根,则 m-n 的值为 .
?
?
6.a是方程2x?=x+4的一个根,则代数式4a?-2a的值是 .
解:∵a是方程2x?=x+4的一个根,
∴2a?-a=4,
∴4a?-2a=2(2a?-a)=2×4=8.
8
7.如图,有一张矩形纸片,长10 cm,宽 6 cm,在它的四角各剪去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面面积是 32 cm2,求剪去的小正方形的边长.设剪去的小正方形的边长是 x cm,根据题意可列方程为( )
A.10×6-4×6x=32
B.(10-2x)(6-2x)=32
C.(10-x)(6-x)=32
D.10×6-4x2=32
B
再 见
同课章节目录
