人教版数学九年级上册课件:24.2.2.5 三角形的内切圆(共17张ppt)
文档属性
| 名称 | 人教版数学九年级上册课件:24.2.2.5 三角形的内切圆(共17张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 645.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 21:19:30 | ||
图片预览



文档简介
三角形的内切圆
学习目标
理解三角形内切圆概念,并会作一个三角形的内切圆,并能利用内切圆或内心进行有关的计算或证明.
学习重点
与三角形内切圆有关的计算和证明.
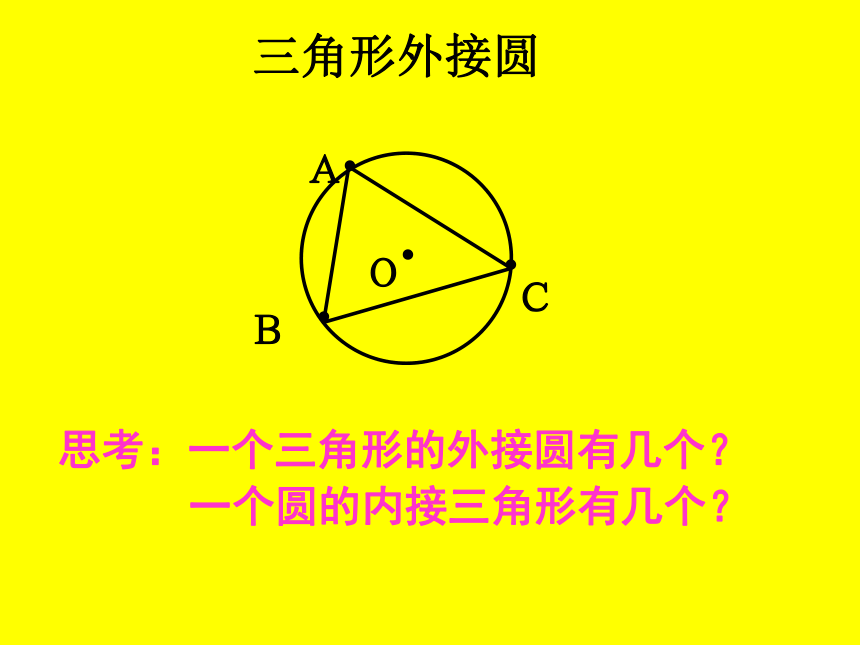
思考:一个三角形的外接圆有几个?
一个圆的内接三角形有几个?
.
.
.
A
B
C
.
O
三角形外接圆
.
o
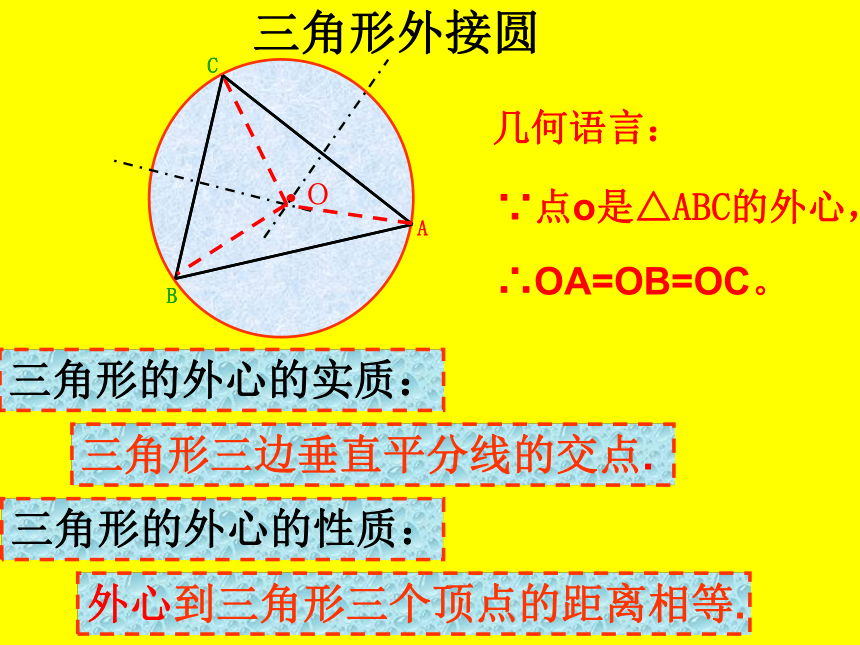
三角形的外心的实质:
三角形外接圆
A
B
C
三角形的外心的性质:
三角形三边垂直平分线的交点.
外心到三角形三个顶点的距离相等.
∵点o是△ABC的外心,
几何语言:
∴OA=OB=OC。
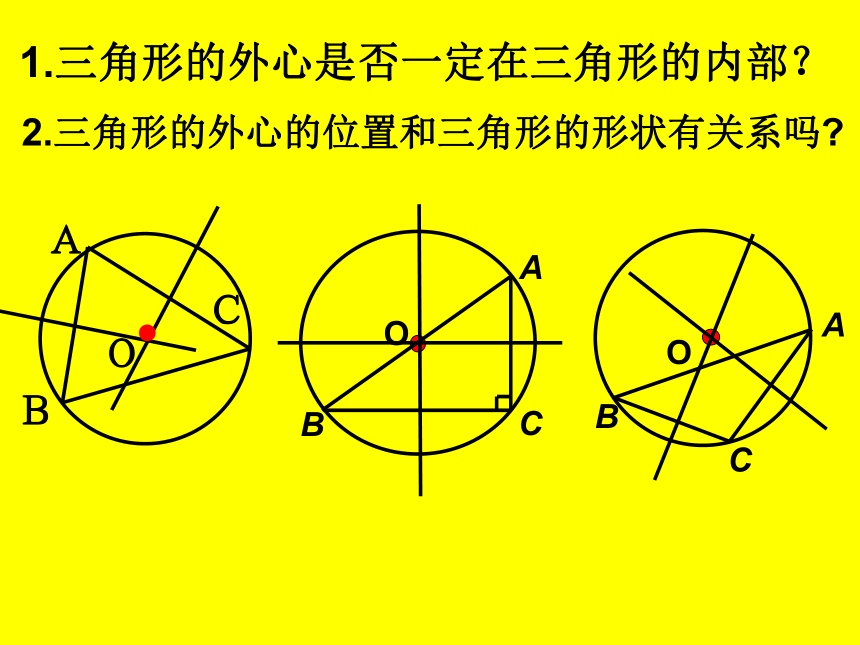
1.三角形的外心是否一定在三角形的内部?
2.三角形的外心的位置和三角形的形状有关系吗?
A
B
C
.
O
O
A
B
C
A
B
C
O
3.作一个角的平分线的方法,把步骤说出来.
回忆:
2.角平分线的判定:
1.角平分线的性质.
A
B
C
创设情境,引入新课
下面是一块三角形的铁皮,如何在它上面截下一块圆形的用料,并且使截下来的圆与三角形的三边都相切?
A
B
C
怎么作圆与三角形的三边都相切?
思考:已知△ABC,求作:⊙O,使⊙O与△ABC的三条边相切(尺规作图,请你在下图中按要求作图)
作法:
1、作∠B、∠C的角平分线,
两线交于点O;
2、过点O作BC的垂线交BC于E;
3、以点O为圆心,OE为半径作圆.
∴⊙O是与△ABC的三条边相切的圆.
知识点一 三角形的内切圆
1、与三角形各边 ,叫做三角形的内切圆,这个三角形叫做圆的 ;
2、内切圆的圆心叫做三角形的 .
都相切的圆
内心
归纳
注意:任何一个三角形有且只有 个内切圆,而任一个圆都有 外切三角形.
外切三角形
三角形内切圆
.
I
A
B
C
三角形的内心的实质:
三角形的内心的性质:
三角形三个内角平分线的交点.
内心到三角形三边的距离相等.
D
E
F
∵点I是△ABC的内心,
几何语言:
∴ ID=IE=IF;
AI平分∠BAC,
CI平分∠ACB
三角形的内心
是否一定在三
角形的内部?
解决问题,加深理解
例、△ABC 的内切圆 ⊙I 与 BC,CA,AB 分别相切于点 D,E,F,且 AB=9,BC=14,CA=13.求 AF,BD,CE 的长.
A
B
C
D
E
F
I
·
B
D
E
F
O
C
A
1、如图,△ABC的内切圆的半径为r, △ABC的周长为l,求△ABC的面积S.
设△ABC的三边为a、b、c,面积为S,
则△ABC的内切圆的半径 r=
2S
a+b+c
知识点二 三角形的内切圆的有关计算
2、如图,Rt△ABC中,∠C=90°,BC=3,AC=4, ⊙I为Rt△ABC的内切圆. 求Rt△ABC的内切圆的半径 .
·
A
B
C
E
D
F
I
·
A
B
C
E
D
F
I
拓展:如图,Rt△ABC中,∠C=90°,BC=a,AC=b, AB=c,⊙I为Rt△ABC的内切圆. 求:Rt△ABC的内切圆的半径 r.
设Rt△ABC的直角边为a、b,斜边为c,则Rt△ABC的
内切圆的半径 r= 或r=
a+b-c
2
ab
a+b+c
练一练
1、如图,△ABC中,∠ABC=50?,∠ACB=76?,点O是△ABC的内心,求∠BOC的度数.
2.直角三角形的外接圆半径为5cm,内切圆半径为1cm,
则此三角形的周长是_______.
3.⊙O是边长为2cm的正方形ABCD的内切圆,EF切⊙O
于P点,交AB、BC于E、F,求△BEF的周长.
E
F
H
G
22cm
学习目标
理解三角形内切圆概念,并会作一个三角形的内切圆,并能利用内切圆或内心进行有关的计算或证明.
学习重点
与三角形内切圆有关的计算和证明.
思考:一个三角形的外接圆有几个?
一个圆的内接三角形有几个?
.
.
.
A
B
C
.
O
三角形外接圆
.
o
三角形的外心的实质:
三角形外接圆
A
B
C
三角形的外心的性质:
三角形三边垂直平分线的交点.
外心到三角形三个顶点的距离相等.
∵点o是△ABC的外心,
几何语言:
∴OA=OB=OC。
1.三角形的外心是否一定在三角形的内部?
2.三角形的外心的位置和三角形的形状有关系吗?
A
B
C
.
O
O
A
B
C
A
B
C
O
3.作一个角的平分线的方法,把步骤说出来.
回忆:
2.角平分线的判定:
1.角平分线的性质.
A
B
C
创设情境,引入新课
下面是一块三角形的铁皮,如何在它上面截下一块圆形的用料,并且使截下来的圆与三角形的三边都相切?
A
B
C
怎么作圆与三角形的三边都相切?
思考:已知△ABC,求作:⊙O,使⊙O与△ABC的三条边相切(尺规作图,请你在下图中按要求作图)
作法:
1、作∠B、∠C的角平分线,
两线交于点O;
2、过点O作BC的垂线交BC于E;
3、以点O为圆心,OE为半径作圆.
∴⊙O是与△ABC的三条边相切的圆.
知识点一 三角形的内切圆
1、与三角形各边 ,叫做三角形的内切圆,这个三角形叫做圆的 ;
2、内切圆的圆心叫做三角形的 .
都相切的圆
内心
归纳
注意:任何一个三角形有且只有 个内切圆,而任一个圆都有 外切三角形.
外切三角形
三角形内切圆
.
I
A
B
C
三角形的内心的实质:
三角形的内心的性质:
三角形三个内角平分线的交点.
内心到三角形三边的距离相等.
D
E
F
∵点I是△ABC的内心,
几何语言:
∴ ID=IE=IF;
AI平分∠BAC,
CI平分∠ACB
三角形的内心
是否一定在三
角形的内部?
解决问题,加深理解
例、△ABC 的内切圆 ⊙I 与 BC,CA,AB 分别相切于点 D,E,F,且 AB=9,BC=14,CA=13.求 AF,BD,CE 的长.
A
B
C
D
E
F
I
·
B
D
E
F
O
C
A
1、如图,△ABC的内切圆的半径为r, △ABC的周长为l,求△ABC的面积S.
设△ABC的三边为a、b、c,面积为S,
则△ABC的内切圆的半径 r=
2S
a+b+c
知识点二 三角形的内切圆的有关计算
2、如图,Rt△ABC中,∠C=90°,BC=3,AC=4, ⊙I为Rt△ABC的内切圆. 求Rt△ABC的内切圆的半径 .
·
A
B
C
E
D
F
I
·
A
B
C
E
D
F
I
拓展:如图,Rt△ABC中,∠C=90°,BC=a,AC=b, AB=c,⊙I为Rt△ABC的内切圆. 求:Rt△ABC的内切圆的半径 r.
设Rt△ABC的直角边为a、b,斜边为c,则Rt△ABC的
内切圆的半径 r= 或r=
a+b-c
2
ab
a+b+c
练一练
1、如图,△ABC中,∠ABC=50?,∠ACB=76?,点O是△ABC的内心,求∠BOC的度数.
2.直角三角形的外接圆半径为5cm,内切圆半径为1cm,
则此三角形的周长是_______.
3.⊙O是边长为2cm的正方形ABCD的内切圆,EF切⊙O
于P点,交AB、BC于E、F,求△BEF的周长.
E
F
H
G
22cm
同课章节目录
