六年级数学下册教案-★ 自行车里的数学-人教版(表格式)
文档属性
| 名称 | 六年级数学下册教案-★ 自行车里的数学-人教版(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 23.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 21:28:13 | ||
图片预览


文档简介
自行车里的数学教案
教学
内容
大 课 题
自行车里的数学
所教年级
六年级
本节内容
自行车里的数学
课程
标准
重要概念
前齿轮齿数X前齿轮转数= 后齿轮的齿数X后齿轮转数
蹬一圈自行车前进的距离=车轮的周长X( 前齿轮齿数÷后齿轮的齿数
内容标准
研究自行车里的数学:前齿轮齿数X前齿轮转数= 后齿轮的齿数X后齿轮转数
蹬一圈自行车前进的距离=车轮的周长X(前齿轮齿数÷后齿轮的齿数)以及变速自行车能变出多少种速度。
课程
目标
三维目标
1、学生通过探究,理解并掌握自行车“蹬一圈能走多远”的计算方法,探索变速自行车的速度与其内部结构的关系,能变化出多少种速度。
2、引领学生经历“提出问题——分析问题——建立数学模型——求解——解释并应用”基本过程,获得应用数学解决实际问题的思考方法。
3、使学生体会数学与生活的紧密联系,增强学生学好数学、用好数学的意识。
重点
难点
重 点
普通自行车的速度与其内在结构的联系。变速自行车能变出多少种速度。
难 点
蹬一圈自行车所走的路程。
学情
分析
自行车里的数学”是在学生刚好学习了正反比例的知识之后安排的一个“综合与实践”活动。本活动是让学生运用所学的圆、比例、排列组合等数学知识来解决实际问题,利用旧知解决新知,学生学起来不是太难,但也有一定的难度。
教学
策略
教法列举
讨论法、讲授法、实验法、练习法
学法列举
合作学习法、探究学习法、自主学习法
教学
准备
自行车里的数学教学ppt
教学过程与教法学法设计
教学
过程
教师活动
(教法)
多媒体
(课件)
学生活动
(学法)
备注
一、谈话引入新课:
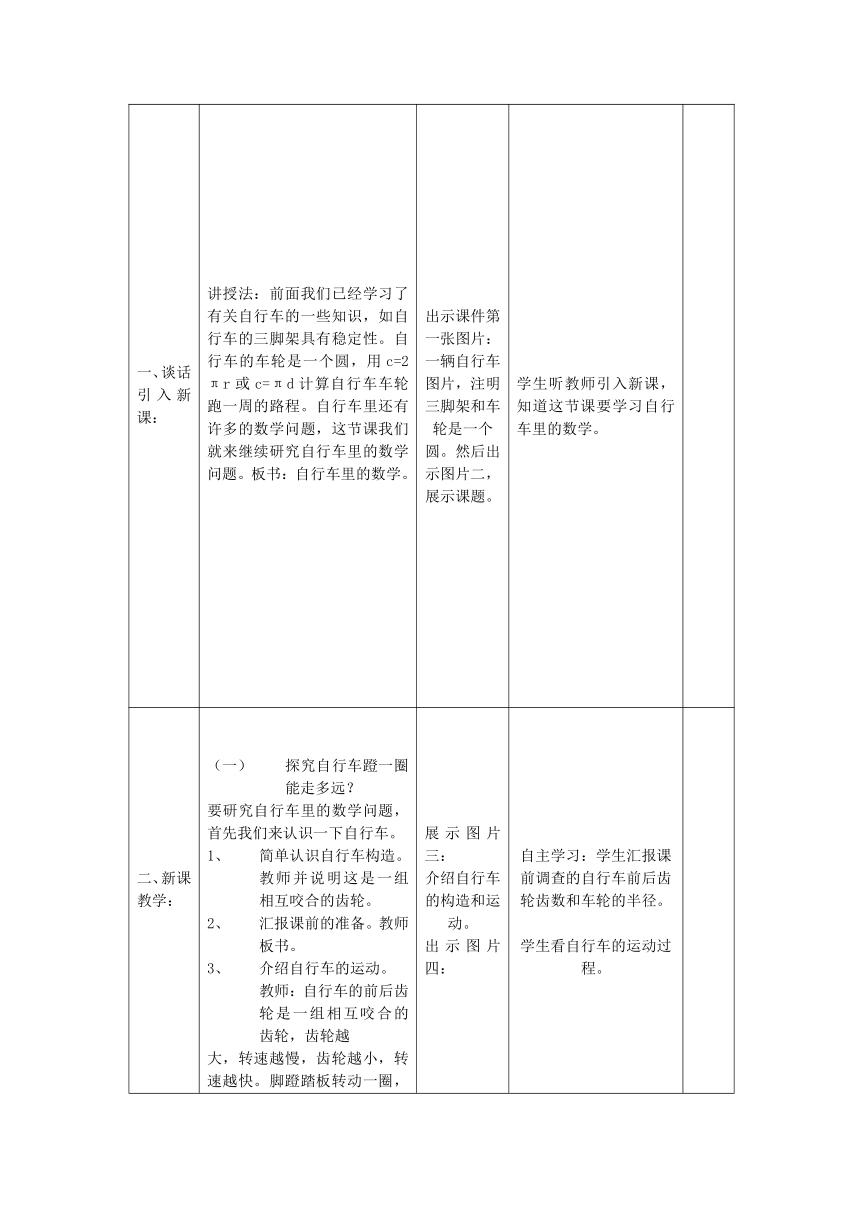
讲授法:前面我们已经学习了有关自行车的一些知识,如自行车的三脚架具有稳定性。自行车的车轮是一个圆,用c=2πr或c=πd计算自行车车轮跑一周的路程。自行车里还有许多的数学问题,这节课我们就来继续研究自行车里的数学问题。板书:自行车里的数学。
出示课件第一张图片:一辆自行车图片,注明三脚架和车轮是一个圆。然后出示图片二,展示课题。
学生听教师引入新课,知道这节课要学习自行车里的数学。
二、新课教学:
探究自行车蹬一圈能走多远?
要研究自行车里的数学问题,首先我们来认识一下自行车。
简单认识自行车构造。
教师并说明这是一组相互咬合的齿轮。
汇报课前的准备。教师板书。
介绍自行车的运动。
教师:自行车的前后齿轮是一组相互咬合的齿轮,齿轮越
大,转速越慢,齿轮越小,转速越快。脚蹬踏板转动一圈,前齿轮转动一圈,通过链条带动后齿轮转动,由于后齿轮是装在车轴上,后齿轮转动带动后轮转动,后轮转动推动前轮转动。
4、了解了自行车的构造和运动,你想提出哪些数学问题?教师板书。
(1)、自行车蹬一圈,能走多远?
(2)、前后齿轮的齿数和转数有怎样的关系?
(3)、自行车有哪些种类?等等。
5、自行车蹬一圈,能走多远?怎样解决这个问题呢?
学生交流讨论,提出方案。
方案一:通过测量来解决。
方案二:用车轮的周长乘(?)轮转的圈数来计算蹬一圈车子走的距离。
用车轮的周长乘(?)轮转的圈数来计算蹬一圈车子走的距离。请同学们研究
学生讨论:
(1)蹬一圈,是什么转动了一圈?
(2)前齿轮转动一圈,后齿轮怎样运动?
(3)车轮转动的圈数实际上是谁转动的圈数?
怎样才能知道前齿轮转动一圈时后齿轮转动的圈数呢?
(4)自行车的前后齿轮是一组相互咬合的齿轮,前齿轮转动2个齿、5个齿、9个齿,后齿轮分别怎么转动?
(5)前齿轮走过的齿数与后齿轮走过的齿数有怎样的关系?
(6) 前齿轮走过的路程与后齿轮走过的齿路程有怎样的关系?
你们发现了什么规律?
前齿轮转动一圈的长度就是链条走过的长度,后轮也要转动同样的长度。所以前齿轮的齿数与转数的乘积等于后齿轮的齿数与转数的乘积。教师板书:前齿轮齿数×前齿轮转数=后齿轮齿数×后齿轮转数。
前齿轮齿数有48个齿,后齿轮齿数24个,前齿轮转动2圈,后齿轮转动几圈?
前齿轮齿数有48个齿,后齿轮齿数16个,后齿轮转动2圈,前齿轮转动几圈?
前齿轮转动1圈,后齿轮的圈数怎样表示?教师板书:后齿轮转数=前齿轮齿数÷后齿轮齿数。
教师总结:自行车蹬一圈走的路程=前齿轮齿数÷后齿轮齿数×车轮的周长。
学生记一记,读一读。
自行车蹬一圈走的路程与哪些因素有关呢?
6、蹬同样的圈数,哪种组合使自行车走得最远?
(1)、学生动手算一算:
前齿轮48个齿,后齿轮24个齿,车轮的直径71厘米。自行车蹬一圈走多少米?
48÷24×3.14×71=445.88厘米
前齿轮48个齿,后齿轮12个齿,车轮的直径71厘米。自行车蹬一圈走多少米?
48÷12×3.14×71=891.76厘米
(2)组织学生讨论:蹬同样的圈数,哪种组合使自行车走得最远?
(3)学生汇报。
(4)教师小结:前后齿轮齿数的比值越大,蹬同样的圈数自行车走得越远。但比较费力,适合跑顺风路(平路和下坡路)。前后齿轮齿数的比值越小,蹬同样的圈数自行车走得越近。但比较省力,适合跑上坡路。
展示图片三:
介绍自行车的构造和运动。
出示图片四:
思考自行车中存在哪些数学问题?和一辆自行车。并出示图片五:展示三个问题。
出示图片六:解决自行车蹬一圈,能走多远?
出示图片七:得出用车轮的周长乘(?)轮转的圈数来计算蹬一圈车子走的距离。
出示图片八:学生讨论三个问题。得出乘后齿轮的转数。
出示图片九:小组合作研究:
前齿轮的齿数与转动的圈数同后齿轮的齿数与转动的圈数之间具有什么关系?
出示图片十:四个问题
出示图片十一:前齿轮齿数×前齿轮转数=后齿轮齿数×后齿轮转数。
出示图片十二得出:自行车蹬一圈走的路程=前齿轮齿数÷后齿轮齿数×车轮的周长。
出示图片十三、十四、十五:计算题。
出示图片十六:比较蹬同样的圈数,哪种组合使自行车走得最远?
自主学习:学生汇报课前调查的自行车前后齿轮齿数和车轮的半径。
学生看自行车的运动过程。
合作学习:学生提出问题。
(1)、自行车蹬一圈,能走多远?
(2)、前后齿轮的齿数和转数有怎样的关系?
(3)、自行车有哪些种类?等等。
学生交流讨论,提出方案。
方案一:通过测量来解决。
方案二:用车轮的周长乘(?)轮转的圈数来计算蹬一圈车子走的距离。
学生交流讨论,提出方案。
方案一:通过测量来解决。
方案二:用车轮的周长乘(?)轮转的圈数来计算蹬一圈车子走的距离。
学生讨论:
(1)蹬一圈,是什么转动了一圈?
(2)前齿轮转动一圈,后齿轮怎样运动?
(3)车轮转动的圈数实际上是谁转动的圈数?
(4)自行车的前后齿轮是一组相互咬合的齿轮,前齿轮转动2个齿、5个齿、9个齿,后齿轮分别怎么转动?
(5)前齿轮走过的齿数与后齿轮走过的齿数有怎样的关系?
(6) 前齿轮走过的路程与后齿轮走过的齿路程有怎样的关系?
学生讨论得出:前齿轮齿数×前齿轮转数=后齿轮齿数×后齿轮转数。
学生得出:自行车蹬一圈走的路程=前齿轮齿数÷后齿轮齿数×车轮的周长。学生记一记,读一读。
1)、学生动手算一算:
前齿轮48个齿,后齿轮24个齿,车轮的直径71厘米。自行车蹬一圈走多少米?
48÷24×3.14×71=445.88厘米
前齿轮48个齿,后齿轮12个齿,车轮的直径71厘米。自行车蹬一圈走多少米?
48÷12×3.14×71=891.76厘米
(2)组织学生讨论:蹬同样的圈数,哪种组合使自行车走得最远?
(3)学生汇报:
前后齿轮齿数的比值越大,蹬同样的圈数自行车走得越远。但比较费力,适合跑顺风路(平路和下坡路)。前后齿轮齿数的比值越小,蹬同样的圈数自行车走得越近。但比较省力,适合跑上坡路。
三、课堂小结。
(三)研究研究变速自行车能组合出多少种速度?
人类很聪明,把几种自行车组合在一起,就造出了变速自行车。
介绍几种变速自行车。提出问题:变速自行车能组合出多少种速度?
了解变速自行车的结构。(有2个前齿轮,6个后齿轮。)
根据这个结构,可以组合出多少种速度?
学生填表格。
蹬同样的圈数,哪种组合走得最远?
学生制造出一种比赛型自行车。
课堂小结
自行车里的学问可真大,这节课我们学习了什么内容?你学到了哪些知识?
出示图片十七、十八:变速自行车能组合出多少种速度?
蹬同样的圈数,哪种组合走得最远?
出示图片十九:制造出一种比赛型自行车。
学生得出变速自行车能组合出12种速度。
学生讨论:蹬同样的圈数,哪种组合走得最远?
学生讨论得出:前后齿轮齿数的比值越大,蹬同样的圈数自行车走得越远。但比较费力,适合跑顺风路(平路和下坡路)。前后齿轮齿数的比值越小,蹬同样的圈数自行车走得越近。但比较省力,适合跑上坡路。
学生制造出一种比赛型自行车。
板书
设计
自行车里的数学
前齿轮走过的齿数=后齿轮走过的齿数
前齿轮走过的路程=后齿轮走过的路程
前齿轮齿数×前齿轮转数=后齿轮齿数×后齿轮转数。
自行车蹬一圈走的路程=前齿轮齿数÷后齿轮齿数×车轮的周长。
课后
反思
“自行车里的数学”是在学生刚好学习了正反比例的知识之后安排的一个“综合与实践”活动。本活动是让学生运用所学的圆、比例、排列组合等数学知识来解决实际问题。“自行车的数学”主要研究两个问题,普通自行车的速度与自行车内在结构的关系;变速自行车能变化出多少种速度。通过这次对自行车里的数学进行研究,学生了解了自行车里的许多数学知识:前后齿轮齿数与它的转数成反比例,前齿轮齿数X前齿轮转数= 后齿轮的齿数X后齿轮转数;蹬一圈自行车前进的距离=车轮的周长X后齿轮转动的圈数
=车轮的周长X( 前齿轮齿数 ÷ 后齿轮的齿数 )等等。
自行车里的数学这部分知识逻辑性特别强,环环相扣。培养了学生的逻辑思维能力。
最后我还给学生出了个难题,制造一辆比赛型自行车。学生还真能说出来,让我非常高兴。能够把所学知识应用到生活实际,让数学生活化。这就是学习自行车里的数学的好处。
自行车的运动就是一种机械运动,现在就是机械的美好时代,各种机器人:无人驾驶的飞机、无人驾驶的汽车等等。希望学生努力学习以后造出高端机械,为人类服务。
在教学时教师既要注重活动的实践性,又要注重学生对问题探究能力的培养。既要充分体现知识的综合应用,又要培养学生综合运用知识的能力。
教学
内容
大 课 题
自行车里的数学
所教年级
六年级
本节内容
自行车里的数学
课程
标准
重要概念
前齿轮齿数X前齿轮转数= 后齿轮的齿数X后齿轮转数
蹬一圈自行车前进的距离=车轮的周长X( 前齿轮齿数÷后齿轮的齿数
内容标准
研究自行车里的数学:前齿轮齿数X前齿轮转数= 后齿轮的齿数X后齿轮转数
蹬一圈自行车前进的距离=车轮的周长X(前齿轮齿数÷后齿轮的齿数)以及变速自行车能变出多少种速度。
课程
目标
三维目标
1、学生通过探究,理解并掌握自行车“蹬一圈能走多远”的计算方法,探索变速自行车的速度与其内部结构的关系,能变化出多少种速度。
2、引领学生经历“提出问题——分析问题——建立数学模型——求解——解释并应用”基本过程,获得应用数学解决实际问题的思考方法。
3、使学生体会数学与生活的紧密联系,增强学生学好数学、用好数学的意识。
重点
难点
重 点
普通自行车的速度与其内在结构的联系。变速自行车能变出多少种速度。
难 点
蹬一圈自行车所走的路程。
学情
分析
自行车里的数学”是在学生刚好学习了正反比例的知识之后安排的一个“综合与实践”活动。本活动是让学生运用所学的圆、比例、排列组合等数学知识来解决实际问题,利用旧知解决新知,学生学起来不是太难,但也有一定的难度。
教学
策略
教法列举
讨论法、讲授法、实验法、练习法
学法列举
合作学习法、探究学习法、自主学习法
教学
准备
自行车里的数学教学ppt
教学过程与教法学法设计
教学
过程
教师活动
(教法)
多媒体
(课件)
学生活动
(学法)
备注
一、谈话引入新课:
讲授法:前面我们已经学习了有关自行车的一些知识,如自行车的三脚架具有稳定性。自行车的车轮是一个圆,用c=2πr或c=πd计算自行车车轮跑一周的路程。自行车里还有许多的数学问题,这节课我们就来继续研究自行车里的数学问题。板书:自行车里的数学。
出示课件第一张图片:一辆自行车图片,注明三脚架和车轮是一个圆。然后出示图片二,展示课题。
学生听教师引入新课,知道这节课要学习自行车里的数学。
二、新课教学:
探究自行车蹬一圈能走多远?
要研究自行车里的数学问题,首先我们来认识一下自行车。
简单认识自行车构造。
教师并说明这是一组相互咬合的齿轮。
汇报课前的准备。教师板书。
介绍自行车的运动。
教师:自行车的前后齿轮是一组相互咬合的齿轮,齿轮越
大,转速越慢,齿轮越小,转速越快。脚蹬踏板转动一圈,前齿轮转动一圈,通过链条带动后齿轮转动,由于后齿轮是装在车轴上,后齿轮转动带动后轮转动,后轮转动推动前轮转动。
4、了解了自行车的构造和运动,你想提出哪些数学问题?教师板书。
(1)、自行车蹬一圈,能走多远?
(2)、前后齿轮的齿数和转数有怎样的关系?
(3)、自行车有哪些种类?等等。
5、自行车蹬一圈,能走多远?怎样解决这个问题呢?
学生交流讨论,提出方案。
方案一:通过测量来解决。
方案二:用车轮的周长乘(?)轮转的圈数来计算蹬一圈车子走的距离。
用车轮的周长乘(?)轮转的圈数来计算蹬一圈车子走的距离。请同学们研究
学生讨论:
(1)蹬一圈,是什么转动了一圈?
(2)前齿轮转动一圈,后齿轮怎样运动?
(3)车轮转动的圈数实际上是谁转动的圈数?
怎样才能知道前齿轮转动一圈时后齿轮转动的圈数呢?
(4)自行车的前后齿轮是一组相互咬合的齿轮,前齿轮转动2个齿、5个齿、9个齿,后齿轮分别怎么转动?
(5)前齿轮走过的齿数与后齿轮走过的齿数有怎样的关系?
(6) 前齿轮走过的路程与后齿轮走过的齿路程有怎样的关系?
你们发现了什么规律?
前齿轮转动一圈的长度就是链条走过的长度,后轮也要转动同样的长度。所以前齿轮的齿数与转数的乘积等于后齿轮的齿数与转数的乘积。教师板书:前齿轮齿数×前齿轮转数=后齿轮齿数×后齿轮转数。
前齿轮齿数有48个齿,后齿轮齿数24个,前齿轮转动2圈,后齿轮转动几圈?
前齿轮齿数有48个齿,后齿轮齿数16个,后齿轮转动2圈,前齿轮转动几圈?
前齿轮转动1圈,后齿轮的圈数怎样表示?教师板书:后齿轮转数=前齿轮齿数÷后齿轮齿数。
教师总结:自行车蹬一圈走的路程=前齿轮齿数÷后齿轮齿数×车轮的周长。
学生记一记,读一读。
自行车蹬一圈走的路程与哪些因素有关呢?
6、蹬同样的圈数,哪种组合使自行车走得最远?
(1)、学生动手算一算:
前齿轮48个齿,后齿轮24个齿,车轮的直径71厘米。自行车蹬一圈走多少米?
48÷24×3.14×71=445.88厘米
前齿轮48个齿,后齿轮12个齿,车轮的直径71厘米。自行车蹬一圈走多少米?
48÷12×3.14×71=891.76厘米
(2)组织学生讨论:蹬同样的圈数,哪种组合使自行车走得最远?
(3)学生汇报。
(4)教师小结:前后齿轮齿数的比值越大,蹬同样的圈数自行车走得越远。但比较费力,适合跑顺风路(平路和下坡路)。前后齿轮齿数的比值越小,蹬同样的圈数自行车走得越近。但比较省力,适合跑上坡路。
展示图片三:
介绍自行车的构造和运动。
出示图片四:
思考自行车中存在哪些数学问题?和一辆自行车。并出示图片五:展示三个问题。
出示图片六:解决自行车蹬一圈,能走多远?
出示图片七:得出用车轮的周长乘(?)轮转的圈数来计算蹬一圈车子走的距离。
出示图片八:学生讨论三个问题。得出乘后齿轮的转数。
出示图片九:小组合作研究:
前齿轮的齿数与转动的圈数同后齿轮的齿数与转动的圈数之间具有什么关系?
出示图片十:四个问题
出示图片十一:前齿轮齿数×前齿轮转数=后齿轮齿数×后齿轮转数。
出示图片十二得出:自行车蹬一圈走的路程=前齿轮齿数÷后齿轮齿数×车轮的周长。
出示图片十三、十四、十五:计算题。
出示图片十六:比较蹬同样的圈数,哪种组合使自行车走得最远?
自主学习:学生汇报课前调查的自行车前后齿轮齿数和车轮的半径。
学生看自行车的运动过程。
合作学习:学生提出问题。
(1)、自行车蹬一圈,能走多远?
(2)、前后齿轮的齿数和转数有怎样的关系?
(3)、自行车有哪些种类?等等。
学生交流讨论,提出方案。
方案一:通过测量来解决。
方案二:用车轮的周长乘(?)轮转的圈数来计算蹬一圈车子走的距离。
学生交流讨论,提出方案。
方案一:通过测量来解决。
方案二:用车轮的周长乘(?)轮转的圈数来计算蹬一圈车子走的距离。
学生讨论:
(1)蹬一圈,是什么转动了一圈?
(2)前齿轮转动一圈,后齿轮怎样运动?
(3)车轮转动的圈数实际上是谁转动的圈数?
(4)自行车的前后齿轮是一组相互咬合的齿轮,前齿轮转动2个齿、5个齿、9个齿,后齿轮分别怎么转动?
(5)前齿轮走过的齿数与后齿轮走过的齿数有怎样的关系?
(6) 前齿轮走过的路程与后齿轮走过的齿路程有怎样的关系?
学生讨论得出:前齿轮齿数×前齿轮转数=后齿轮齿数×后齿轮转数。
学生得出:自行车蹬一圈走的路程=前齿轮齿数÷后齿轮齿数×车轮的周长。学生记一记,读一读。
1)、学生动手算一算:
前齿轮48个齿,后齿轮24个齿,车轮的直径71厘米。自行车蹬一圈走多少米?
48÷24×3.14×71=445.88厘米
前齿轮48个齿,后齿轮12个齿,车轮的直径71厘米。自行车蹬一圈走多少米?
48÷12×3.14×71=891.76厘米
(2)组织学生讨论:蹬同样的圈数,哪种组合使自行车走得最远?
(3)学生汇报:
前后齿轮齿数的比值越大,蹬同样的圈数自行车走得越远。但比较费力,适合跑顺风路(平路和下坡路)。前后齿轮齿数的比值越小,蹬同样的圈数自行车走得越近。但比较省力,适合跑上坡路。
三、课堂小结。
(三)研究研究变速自行车能组合出多少种速度?
人类很聪明,把几种自行车组合在一起,就造出了变速自行车。
介绍几种变速自行车。提出问题:变速自行车能组合出多少种速度?
了解变速自行车的结构。(有2个前齿轮,6个后齿轮。)
根据这个结构,可以组合出多少种速度?
学生填表格。
蹬同样的圈数,哪种组合走得最远?
学生制造出一种比赛型自行车。
课堂小结
自行车里的学问可真大,这节课我们学习了什么内容?你学到了哪些知识?
出示图片十七、十八:变速自行车能组合出多少种速度?
蹬同样的圈数,哪种组合走得最远?
出示图片十九:制造出一种比赛型自行车。
学生得出变速自行车能组合出12种速度。
学生讨论:蹬同样的圈数,哪种组合走得最远?
学生讨论得出:前后齿轮齿数的比值越大,蹬同样的圈数自行车走得越远。但比较费力,适合跑顺风路(平路和下坡路)。前后齿轮齿数的比值越小,蹬同样的圈数自行车走得越近。但比较省力,适合跑上坡路。
学生制造出一种比赛型自行车。
板书
设计
自行车里的数学
前齿轮走过的齿数=后齿轮走过的齿数
前齿轮走过的路程=后齿轮走过的路程
前齿轮齿数×前齿轮转数=后齿轮齿数×后齿轮转数。
自行车蹬一圈走的路程=前齿轮齿数÷后齿轮齿数×车轮的周长。
课后
反思
“自行车里的数学”是在学生刚好学习了正反比例的知识之后安排的一个“综合与实践”活动。本活动是让学生运用所学的圆、比例、排列组合等数学知识来解决实际问题。“自行车的数学”主要研究两个问题,普通自行车的速度与自行车内在结构的关系;变速自行车能变化出多少种速度。通过这次对自行车里的数学进行研究,学生了解了自行车里的许多数学知识:前后齿轮齿数与它的转数成反比例,前齿轮齿数X前齿轮转数= 后齿轮的齿数X后齿轮转数;蹬一圈自行车前进的距离=车轮的周长X后齿轮转动的圈数
=车轮的周长X( 前齿轮齿数 ÷ 后齿轮的齿数 )等等。
自行车里的数学这部分知识逻辑性特别强,环环相扣。培养了学生的逻辑思维能力。
最后我还给学生出了个难题,制造一辆比赛型自行车。学生还真能说出来,让我非常高兴。能够把所学知识应用到生活实际,让数学生活化。这就是学习自行车里的数学的好处。
自行车的运动就是一种机械运动,现在就是机械的美好时代,各种机器人:无人驾驶的飞机、无人驾驶的汽车等等。希望学生努力学习以后造出高端机械,为人类服务。
在教学时教师既要注重活动的实践性,又要注重学生对问题探究能力的培养。既要充分体现知识的综合应用,又要培养学生综合运用知识的能力。
