2020-2021学年沪科版八年级数学下册第19章四边形达标测试卷(含答案)
文档属性
| 名称 | 2020-2021学年沪科版八年级数学下册第19章四边形达标测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 176.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 08:15:16 | ||
图片预览



文档简介
第19章《四边形》达标测试卷
一、选择题(每题3分,共30分)
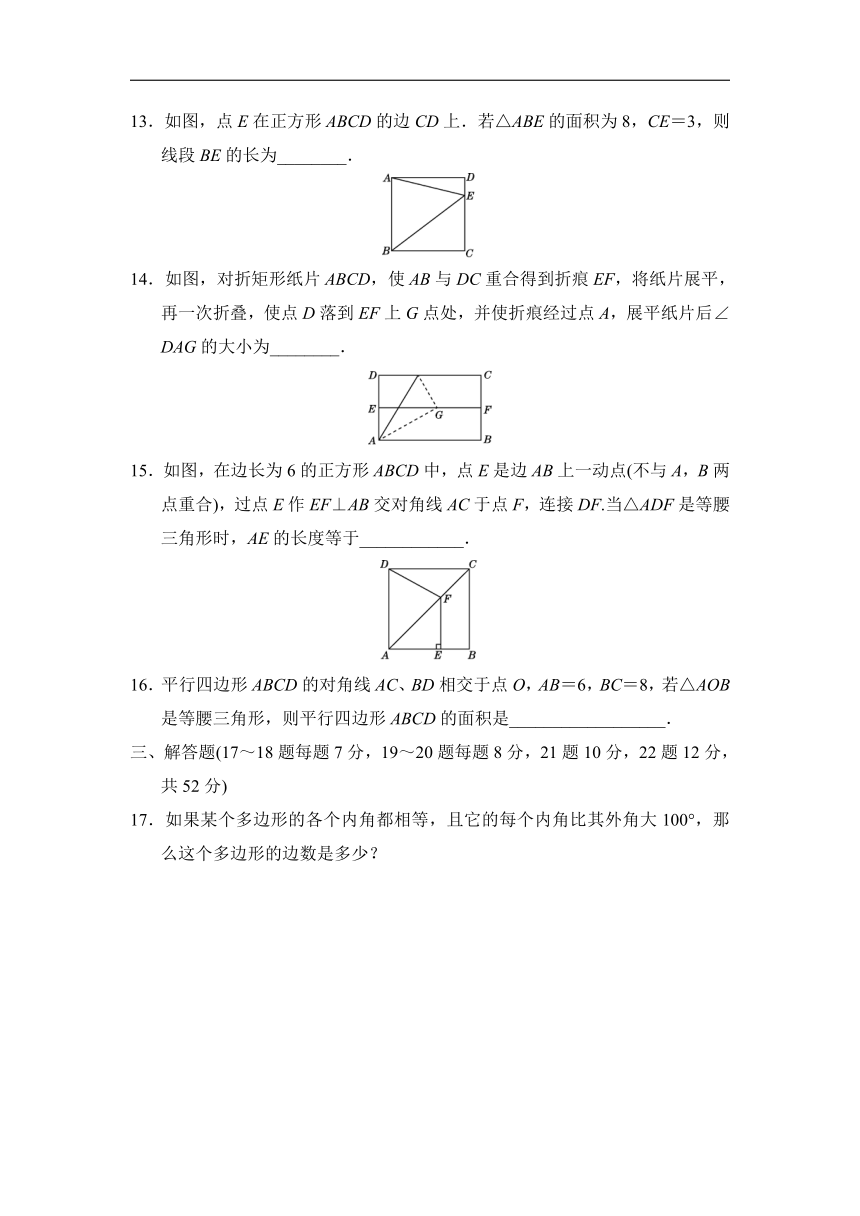
1.下列图形中不是凸多边形的是( )
2.一个多边形的内角和与外角和的和为540°,则它是( )
A.五边形
B.四边形
C.三角形
D.无法确定
3.如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )
A.40
B.24
C.20
D.15
4.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.AB∥CD,AB=CD
C.AB∥CD,AD∥BC
D.AB=CD,AD∥BC
5.如图,在Rt△ABC中,
∠A=90°,AB=3,AC=4,P是BC边上的一点,作PE⊥AB于点E,PF⊥AC于点F,则EF的最小值是( )
A.2
B.2.2
C.2.4
D.2.5
6.设四边形的内角和等于a,六边形的外角和等于b,则a-b等于( )
A.180°
B.-180°
C.0°
D.360°
7.如图,已知凸五边形ABCDE的边长均相等,且∠DBE=∠ABE+∠CBD,AC=1,则BD必定满足( )
A.BD<2
B.BD=2
C.BD>2
D.BD=3
8.如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )
A.∠ECD=112.5°
B.DE平分∠FDC
C.∠DEC=30°
D.AB=CD
9.如图,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD的度数是( )
A.
7°
B.21°
C.23°
D.24°
10.如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为点G,连接CG,下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值为-1.其中正确的说法有( )
A.4个
B.3个
C.2个
D.1个
二、填空题(每题3分,共18分)
11.用正多边形镶嵌一个平面,若每个顶点周围有m个正方形,n个正八边形,则m+n=________.
12.如图,在?ABCD中,对角线AC,BD相交于点O,点E是AB的中点,OE=5
cm,则AD的长为________cm.
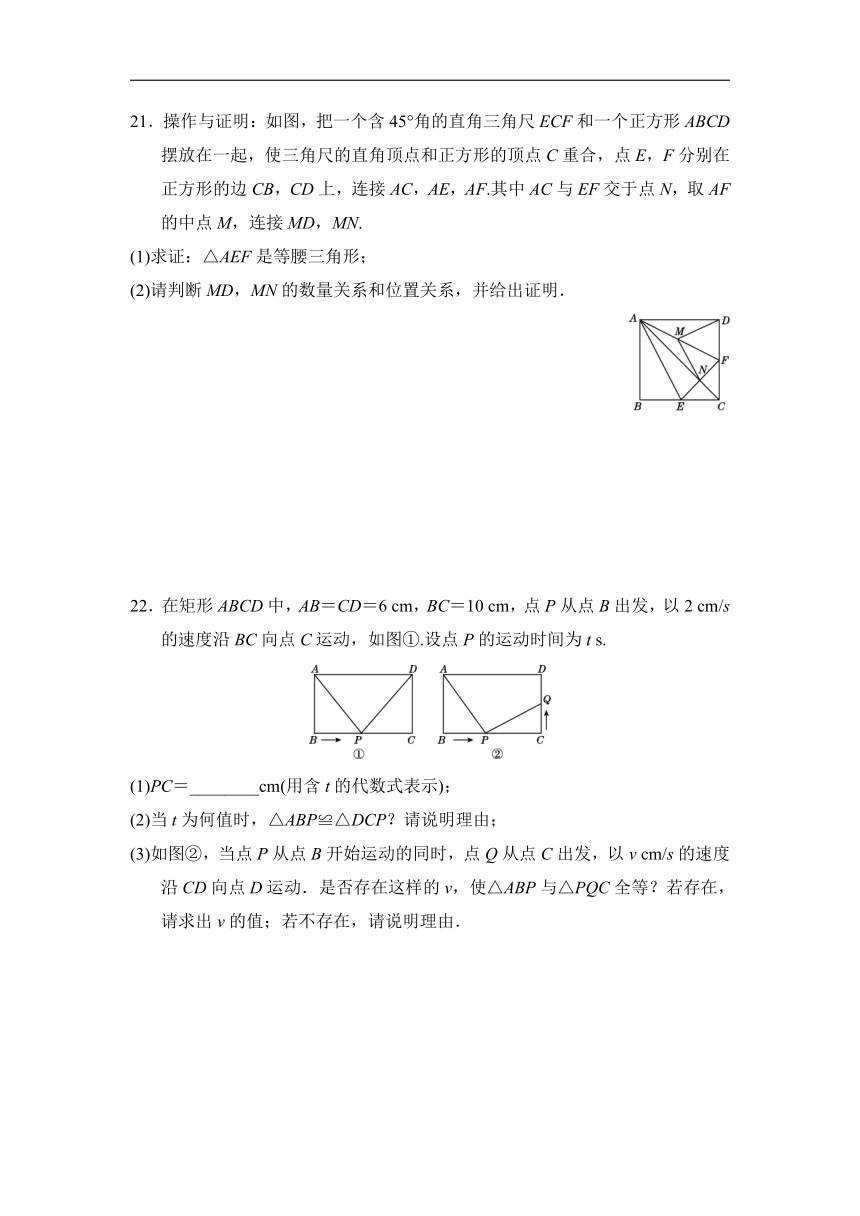
13.如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为________.
14.如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平,再一次折叠,使点D落到EF上G点处,并使折痕经过点A,展平纸片后∠DAG的大小为________.
15.如图,在边长为6的正方形ABCD中,点E是边AB上一动点(不与A,B两点重合),过点E作EF⊥AB交对角线AC于点F,连接DF.当△ADF是等腰三角形时,AE的长度等于____________.
16.平行四边形ABCD的对角线AC、BD相交于点O,AB=6,BC=8,若△AOB是等腰三角形,则平行四边形ABCD的面积是__________________.
三、解答题(17~18题每题7分,19~20题每题8分,21题10分,22题12分,共52分)
17.如果某个多边形的各个内角都相等,且它的每个内角比其外角大100°,那么这个多边形的边数是多少?
18.如图,在?ABCD中,AC,BD相交于点O,点E在AB上,点F在CD上,EF经过点O.求证:四边形BEDF是平行四边形.
19.如图,在四边形ABCD中,AD∥BC,AB=BC,对角线AC,BD交于点O,BD平分∠ABC,过点D作DE⊥BC,交BC的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若DC=,AC=2,求OE的长.
20.如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC的外角∠CAM的平分线,CE⊥AN,垂足为点E.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
21.操作与证明:如图,把一个含45°角的直角三角尺ECF和一个正方形ABCD摆放在一起,使三角尺的直角顶点和正方形的顶点C重合,点E,F分别在正方形的边CB,CD上,连接AC,AE,AF.其中AC与EF交于点N,取AF的中点M,连接MD,MN.
(1)求证:△AEF是等腰三角形;
(2)请判断MD,MN的数量关系和位置关系,并给出证明.
22.在矩形ABCD中,AB=CD=6
cm,BC=10
cm,点P从点B出发,以2
cm/s的速度沿BC向点C运动,如图①.设点P的运动时间为t
s.
(1)PC=________cm(用含t的代数式表示);
(2)当t为何值时,△ABP≌△DCP?请说明理由;
(3)如图②,当点P从点B开始运动的同时,点Q从点C出发,以v
cm/s的速度沿CD向点D运动.是否存在这样的v,使△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
答案
一、1.A 2.C 3.B 4.D 5.C 6.C
7.A 点拨:∵AE=AB,
∴∠ABE=∠AEB,
同理∠CBD=∠CDB.
∵∠DBE=∠ABE+∠CBD,
∴∠DBE=∠AEB+∠CDB,
∴∠AED+∠CDE=180°,
∴AE∥CD.∵AE=CD,
∴四边形AEDC为平行四边形.
∴BC=CD=DE=AC=1.
在△BCD中,∵BD<BC+CD,
∴BD<2.故选A.
8.C 点拨:∵AB=AC,∠CAB=45°,
∴∠B=∠ACB=67.5°.∵∠CAD=45°,∠ADC=90°,∴∠ACD=45°,
∴AD=DC,∠ECD=∠ACB+∠ACD=112.5°,故A正确;∵E,F分别是BC,AC的中点,∴FE=AB,FE∥AB,∴∠EFC=∠BAC=45°,∠FEC=∠B=67.5°.由F是AC的中点,∠ADC=90°,AD=DC,易知FD=AC,DF⊥AC,∠FDC=45°.∵AB=AC,∴FE=FD,∴∠FDE=∠FED=(180°-∠EFD)=(180°-90°-45°)=22.5°,∴∠FDE=∠FDC,∴DE平分∠FDC,故B正确;∵∠FEC=67.5°,∠FED=22.5°,∴∠DEC=∠FEC-∠FED=45°,故C错误;∵∠ADC=90°,AD=DC,∴AC=CD.又∵AB=AC,∴AB=CD,故D正确.故选C.
9.C 点拨:在矩形ABCD中,AB∥CD,∠BCD=90°,所以∠FEA=∠ECD,∠ACD=90°-∠ACB=69°.因为∠ACF=∠AFC,∠FAE=∠FEA,∠AFC=∠FAE+∠FEA,所以∠ACF=2∠FEA,所以∠ACD=∠ACF+∠ECD=3∠ECD=69°,所以∠ECD=23°.故选C.
10.C 点拨:当点E与点C重合时,AG=GE,故①错误;∵四边形ABCD为正方形,∴AB=BC,∠ABE=∠BCF=90°.∵BF⊥AE,∴∠BAG+∠ABG=90°.又∵∠ABG+∠GBE=90°,∴∠GBE=∠BAG.在△ABE和△BCF中,
∵
∴△ABE≌△BCF,∴AE=BF,故②正确;
由题意知点G运动的轨迹是以AB为直径的圆弧.
∵AB=2,∴圆弧的长为×2×π=π.故③错误.
当直线CG过AB的中点时,CG取得最小值.
此时CG=-1,故④正确.
二、11.3 12.10 13.5
14.60° 点拨:如图所示:
由题意易得∠1=∠2,AN=MN,∠MGA=90°,
∴NG=AM,∴AN=NG,∴∠2=∠4.
∵EF∥AB,∴∠4=∠3,
∴∠1=∠2=∠3=×90°=30°,∴∠DAG=60°.
15.3
或3 点拨:①当AF=AD=6时,易知AF=AE,∴AE=3
;②当AF=DF时,△ADF是等腰直角三角形,∴AD=AF=6,∴AF=3
.在等腰直角三角形AEF中,AF=AE,∴AE=3;③当AD=DF时,∠AFD=45°,此时点F与点C重合,点E与点B重合,不符合题意.综上所述,当△ADF是等腰三角形时,AE的长度等于3
或3.
16.48或2
点拨:①当OA=OB时,如图①.
∵OA=OB,∴AC=BD,
∴四边形ABCD是矩形,
∴四边形ABCD的面积是48;
②当AB=AO=OC=6时,作AH⊥CB交CB的延长线于H,如图②.
设HC=x.
∵AH2=AB2-BH2=AC2-CH2,
∴62-(x-8)2=122-x2,∴x=,∴AH=,
∴四边形ABCD的面积为8×=2;
③当AB=OB时,与②的解题过程类似,可得四边形ABCD的面积为2.
综上所述,四边形ABCD的面积是48或2.
三、17.解:设每个内角的度数为x,边数为n,则x-(180°-x)=100°,
解得x=140°.
∴(n-2)·180°=140°·n,解得n=9.即这个多边形的边数是9.
18.证明:在?ABCD中,DC∥AB,OD=OB,
∴∠FDO=∠EBO,∠DFO=∠BEO.
∴△ODF≌△OBE,∴OF=OE,∴四边形BEDF是平行四边形.
19.(1)证明:∵AD∥BC,∴∠ADB=∠CBD.
∵BD平分∠ABC,∴∠ABD=∠CBD,
∴∠ADB=∠ABD,∴AD=AB.
∵AB=BC,∴AD=BC.
又∵AD∥BC,∴四边形ABCD是平行四边形.
又∵AB=BC,∴四边形ABCD是菱形.
(2)解:∵四边形ABCD是菱形,∴AC⊥BD,OB=OD,OA=OC=AC=1.
在Rt△OCD中,由勾股定理得OD==2,∴BD=2OD=4.
∵DE⊥BC,∴∠DEB=90°.
∵OB=OD,∴OE=BD=2.
20.(1)证明:∵在△ABC中,AB=AC,AD⊥BC,∴∠BAD=∠DAC.
∵AN是△ABC的外角∠CAM的平分线,∴∠MAE=∠CAE,
∴∠DAE=∠DAC+∠CAE=×180°=90°.
又∵AD⊥BC,CE⊥AN,∴∠ADC=∠CEA=90°,∴四边形ADCE为矩形.
(2)解:当△ABC满足∠BAC=90°时,四边形ADCE是正方形.证明如下:
由(1)知∠BAD=∠DAC,四边形ADCE是矩形.
∵∠BAC=90°,∴∠DAC=45°,∴∠DCA=45°,
∴DC=AD.
∴四边形ADCE是正方形.
21.(1)证明:∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠ABE=∠ADF=90°.
∵△EFC是等腰直角三角形,∴CE=CF,∴BE=DF,
∴△ABE≌△ADF,∴AE=AF,∴△AEF是等腰三角形.
(2)解:MD=MN,且MD⊥MN.
证明:在Rt△ADF中,
∵M是AF的中点,∴DM=AF.
∵EC=FC,CA平分∠ECF,∴AC⊥EF,EN=FN,∴∠ANF=90°,
∴MN=AF,∴MD=MN.
由(1)知△ABE≌△ADF,∴∠BAE=∠FAD.
∵DM=AF=AM,∴∠FAD=∠ADM,
∴∠FMD=∠FAD+∠ADM=2∠FAD.
∵AM=FM,EN=FN,∴MN∥AE,∴∠FMN=∠EAF.
∵∠BAD=∠EAF+∠BAE+∠FAD=∠EAF+2∠FAD=90°,
∴∠DMN=∠FMN+∠FMD=∠EAF+2∠FAD=90°,
∴MD⊥MN.
22.解:(1)(10-2t)
(2)当t=2.5时,△ABP≌△DCP.
理由如下:
当t=2.5时,BP=2×2.5=5(cm),∴PC=10-5=5(cm).∴BP=PC.
在△ABP和△DCP中,
∴△ABP≌△DCP(SAS).
(3)存在.
①当△ABP≌△PCQ时,AB=PC,BP=CQ.
即10-2t=6,2t=vt.解得t=2,v=2.
②当△ABP≌△QCP时,AB=QC,BP=CP.
即vt=6,2t=10-2t.解得t=2.5,v=2.4.
综上所述,v=2或2.4.
一、选择题(每题3分,共30分)
1.下列图形中不是凸多边形的是( )
2.一个多边形的内角和与外角和的和为540°,则它是( )
A.五边形
B.四边形
C.三角形
D.无法确定
3.如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )
A.40
B.24
C.20
D.15
4.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.AB∥CD,AB=CD
C.AB∥CD,AD∥BC
D.AB=CD,AD∥BC
5.如图,在Rt△ABC中,
∠A=90°,AB=3,AC=4,P是BC边上的一点,作PE⊥AB于点E,PF⊥AC于点F,则EF的最小值是( )
A.2
B.2.2
C.2.4
D.2.5
6.设四边形的内角和等于a,六边形的外角和等于b,则a-b等于( )
A.180°
B.-180°
C.0°
D.360°
7.如图,已知凸五边形ABCDE的边长均相等,且∠DBE=∠ABE+∠CBD,AC=1,则BD必定满足( )
A.BD<2
B.BD=2
C.BD>2
D.BD=3
8.如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )
A.∠ECD=112.5°
B.DE平分∠FDC
C.∠DEC=30°
D.AB=CD
9.如图,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD的度数是( )
A.
7°
B.21°
C.23°
D.24°
10.如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为点G,连接CG,下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值为-1.其中正确的说法有( )
A.4个
B.3个
C.2个
D.1个
二、填空题(每题3分,共18分)
11.用正多边形镶嵌一个平面,若每个顶点周围有m个正方形,n个正八边形,则m+n=________.
12.如图,在?ABCD中,对角线AC,BD相交于点O,点E是AB的中点,OE=5
cm,则AD的长为________cm.
13.如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为________.
14.如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平,再一次折叠,使点D落到EF上G点处,并使折痕经过点A,展平纸片后∠DAG的大小为________.
15.如图,在边长为6的正方形ABCD中,点E是边AB上一动点(不与A,B两点重合),过点E作EF⊥AB交对角线AC于点F,连接DF.当△ADF是等腰三角形时,AE的长度等于____________.
16.平行四边形ABCD的对角线AC、BD相交于点O,AB=6,BC=8,若△AOB是等腰三角形,则平行四边形ABCD的面积是__________________.
三、解答题(17~18题每题7分,19~20题每题8分,21题10分,22题12分,共52分)
17.如果某个多边形的各个内角都相等,且它的每个内角比其外角大100°,那么这个多边形的边数是多少?
18.如图,在?ABCD中,AC,BD相交于点O,点E在AB上,点F在CD上,EF经过点O.求证:四边形BEDF是平行四边形.
19.如图,在四边形ABCD中,AD∥BC,AB=BC,对角线AC,BD交于点O,BD平分∠ABC,过点D作DE⊥BC,交BC的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若DC=,AC=2,求OE的长.
20.如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC的外角∠CAM的平分线,CE⊥AN,垂足为点E.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
21.操作与证明:如图,把一个含45°角的直角三角尺ECF和一个正方形ABCD摆放在一起,使三角尺的直角顶点和正方形的顶点C重合,点E,F分别在正方形的边CB,CD上,连接AC,AE,AF.其中AC与EF交于点N,取AF的中点M,连接MD,MN.
(1)求证:△AEF是等腰三角形;
(2)请判断MD,MN的数量关系和位置关系,并给出证明.
22.在矩形ABCD中,AB=CD=6
cm,BC=10
cm,点P从点B出发,以2
cm/s的速度沿BC向点C运动,如图①.设点P的运动时间为t
s.
(1)PC=________cm(用含t的代数式表示);
(2)当t为何值时,△ABP≌△DCP?请说明理由;
(3)如图②,当点P从点B开始运动的同时,点Q从点C出发,以v
cm/s的速度沿CD向点D运动.是否存在这样的v,使△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
答案
一、1.A 2.C 3.B 4.D 5.C 6.C
7.A 点拨:∵AE=AB,
∴∠ABE=∠AEB,
同理∠CBD=∠CDB.
∵∠DBE=∠ABE+∠CBD,
∴∠DBE=∠AEB+∠CDB,
∴∠AED+∠CDE=180°,
∴AE∥CD.∵AE=CD,
∴四边形AEDC为平行四边形.
∴BC=CD=DE=AC=1.
在△BCD中,∵BD<BC+CD,
∴BD<2.故选A.
8.C 点拨:∵AB=AC,∠CAB=45°,
∴∠B=∠ACB=67.5°.∵∠CAD=45°,∠ADC=90°,∴∠ACD=45°,
∴AD=DC,∠ECD=∠ACB+∠ACD=112.5°,故A正确;∵E,F分别是BC,AC的中点,∴FE=AB,FE∥AB,∴∠EFC=∠BAC=45°,∠FEC=∠B=67.5°.由F是AC的中点,∠ADC=90°,AD=DC,易知FD=AC,DF⊥AC,∠FDC=45°.∵AB=AC,∴FE=FD,∴∠FDE=∠FED=(180°-∠EFD)=(180°-90°-45°)=22.5°,∴∠FDE=∠FDC,∴DE平分∠FDC,故B正确;∵∠FEC=67.5°,∠FED=22.5°,∴∠DEC=∠FEC-∠FED=45°,故C错误;∵∠ADC=90°,AD=DC,∴AC=CD.又∵AB=AC,∴AB=CD,故D正确.故选C.
9.C 点拨:在矩形ABCD中,AB∥CD,∠BCD=90°,所以∠FEA=∠ECD,∠ACD=90°-∠ACB=69°.因为∠ACF=∠AFC,∠FAE=∠FEA,∠AFC=∠FAE+∠FEA,所以∠ACF=2∠FEA,所以∠ACD=∠ACF+∠ECD=3∠ECD=69°,所以∠ECD=23°.故选C.
10.C 点拨:当点E与点C重合时,AG=GE,故①错误;∵四边形ABCD为正方形,∴AB=BC,∠ABE=∠BCF=90°.∵BF⊥AE,∴∠BAG+∠ABG=90°.又∵∠ABG+∠GBE=90°,∴∠GBE=∠BAG.在△ABE和△BCF中,
∵
∴△ABE≌△BCF,∴AE=BF,故②正确;
由题意知点G运动的轨迹是以AB为直径的圆弧.
∵AB=2,∴圆弧的长为×2×π=π.故③错误.
当直线CG过AB的中点时,CG取得最小值.
此时CG=-1,故④正确.
二、11.3 12.10 13.5
14.60° 点拨:如图所示:
由题意易得∠1=∠2,AN=MN,∠MGA=90°,
∴NG=AM,∴AN=NG,∴∠2=∠4.
∵EF∥AB,∴∠4=∠3,
∴∠1=∠2=∠3=×90°=30°,∴∠DAG=60°.
15.3
或3 点拨:①当AF=AD=6时,易知AF=AE,∴AE=3
;②当AF=DF时,△ADF是等腰直角三角形,∴AD=AF=6,∴AF=3
.在等腰直角三角形AEF中,AF=AE,∴AE=3;③当AD=DF时,∠AFD=45°,此时点F与点C重合,点E与点B重合,不符合题意.综上所述,当△ADF是等腰三角形时,AE的长度等于3
或3.
16.48或2
点拨:①当OA=OB时,如图①.
∵OA=OB,∴AC=BD,
∴四边形ABCD是矩形,
∴四边形ABCD的面积是48;
②当AB=AO=OC=6时,作AH⊥CB交CB的延长线于H,如图②.
设HC=x.
∵AH2=AB2-BH2=AC2-CH2,
∴62-(x-8)2=122-x2,∴x=,∴AH=,
∴四边形ABCD的面积为8×=2;
③当AB=OB时,与②的解题过程类似,可得四边形ABCD的面积为2.
综上所述,四边形ABCD的面积是48或2.
三、17.解:设每个内角的度数为x,边数为n,则x-(180°-x)=100°,
解得x=140°.
∴(n-2)·180°=140°·n,解得n=9.即这个多边形的边数是9.
18.证明:在?ABCD中,DC∥AB,OD=OB,
∴∠FDO=∠EBO,∠DFO=∠BEO.
∴△ODF≌△OBE,∴OF=OE,∴四边形BEDF是平行四边形.
19.(1)证明:∵AD∥BC,∴∠ADB=∠CBD.
∵BD平分∠ABC,∴∠ABD=∠CBD,
∴∠ADB=∠ABD,∴AD=AB.
∵AB=BC,∴AD=BC.
又∵AD∥BC,∴四边形ABCD是平行四边形.
又∵AB=BC,∴四边形ABCD是菱形.
(2)解:∵四边形ABCD是菱形,∴AC⊥BD,OB=OD,OA=OC=AC=1.
在Rt△OCD中,由勾股定理得OD==2,∴BD=2OD=4.
∵DE⊥BC,∴∠DEB=90°.
∵OB=OD,∴OE=BD=2.
20.(1)证明:∵在△ABC中,AB=AC,AD⊥BC,∴∠BAD=∠DAC.
∵AN是△ABC的外角∠CAM的平分线,∴∠MAE=∠CAE,
∴∠DAE=∠DAC+∠CAE=×180°=90°.
又∵AD⊥BC,CE⊥AN,∴∠ADC=∠CEA=90°,∴四边形ADCE为矩形.
(2)解:当△ABC满足∠BAC=90°时,四边形ADCE是正方形.证明如下:
由(1)知∠BAD=∠DAC,四边形ADCE是矩形.
∵∠BAC=90°,∴∠DAC=45°,∴∠DCA=45°,
∴DC=AD.
∴四边形ADCE是正方形.
21.(1)证明:∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠ABE=∠ADF=90°.
∵△EFC是等腰直角三角形,∴CE=CF,∴BE=DF,
∴△ABE≌△ADF,∴AE=AF,∴△AEF是等腰三角形.
(2)解:MD=MN,且MD⊥MN.
证明:在Rt△ADF中,
∵M是AF的中点,∴DM=AF.
∵EC=FC,CA平分∠ECF,∴AC⊥EF,EN=FN,∴∠ANF=90°,
∴MN=AF,∴MD=MN.
由(1)知△ABE≌△ADF,∴∠BAE=∠FAD.
∵DM=AF=AM,∴∠FAD=∠ADM,
∴∠FMD=∠FAD+∠ADM=2∠FAD.
∵AM=FM,EN=FN,∴MN∥AE,∴∠FMN=∠EAF.
∵∠BAD=∠EAF+∠BAE+∠FAD=∠EAF+2∠FAD=90°,
∴∠DMN=∠FMN+∠FMD=∠EAF+2∠FAD=90°,
∴MD⊥MN.
22.解:(1)(10-2t)
(2)当t=2.5时,△ABP≌△DCP.
理由如下:
当t=2.5时,BP=2×2.5=5(cm),∴PC=10-5=5(cm).∴BP=PC.
在△ABP和△DCP中,
∴△ABP≌△DCP(SAS).
(3)存在.
①当△ABP≌△PCQ时,AB=PC,BP=CQ.
即10-2t=6,2t=vt.解得t=2,v=2.
②当△ABP≌△QCP时,AB=QC,BP=CP.
即vt=6,2t=10-2t.解得t=2.5,v=2.4.
综上所述,v=2或2.4.
