人教版八年级上册课件 13.1.2 线段的垂直平分线性质(1)(共15张ppt)
文档属性
| 名称 | 人教版八年级上册课件 13.1.2 线段的垂直平分线性质(1)(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 303.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 07:19:48 | ||
图片预览



文档简介
(共15张PPT)
13.1.2线段的垂直平分线的性质(1)
授课人:林爱弟
学习目标:
1、探究线段垂直平分线的性质定理
2、经历探索线段垂直平分线的性质的过程,培养认真探究、积极思考的能力
重难点:线段垂直平分线的性质定理的应用
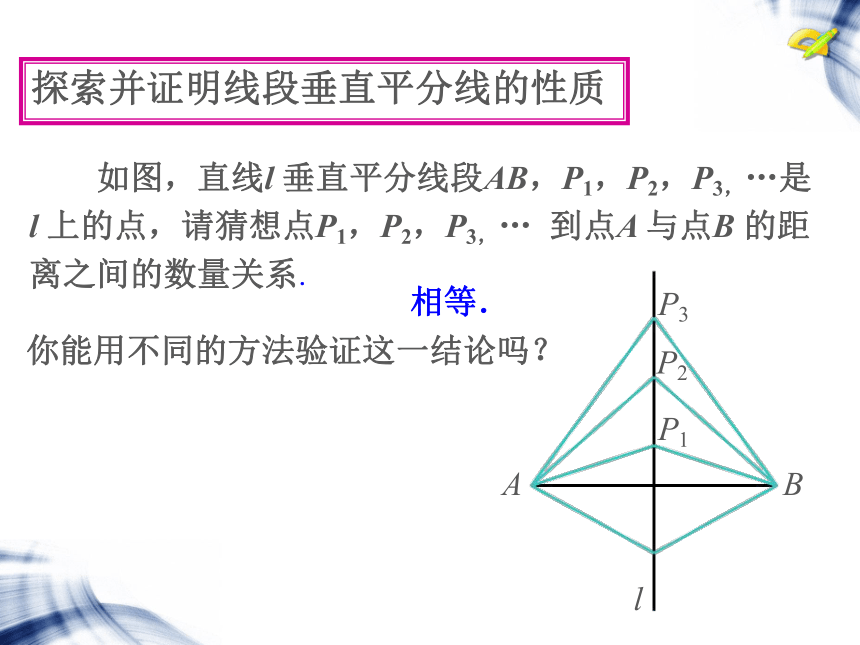
你能用不同的方法验证这一结论吗?
探索并证明线段垂直平分线的性质
如图,直线l
垂直平分线段AB,P1,P2,P3,…是
l
上的点,请猜想点P1,P2,P3,…
到点A
与点B
的距
离之间的数量关系.
相等.
A
B
l
P1
P2
P3
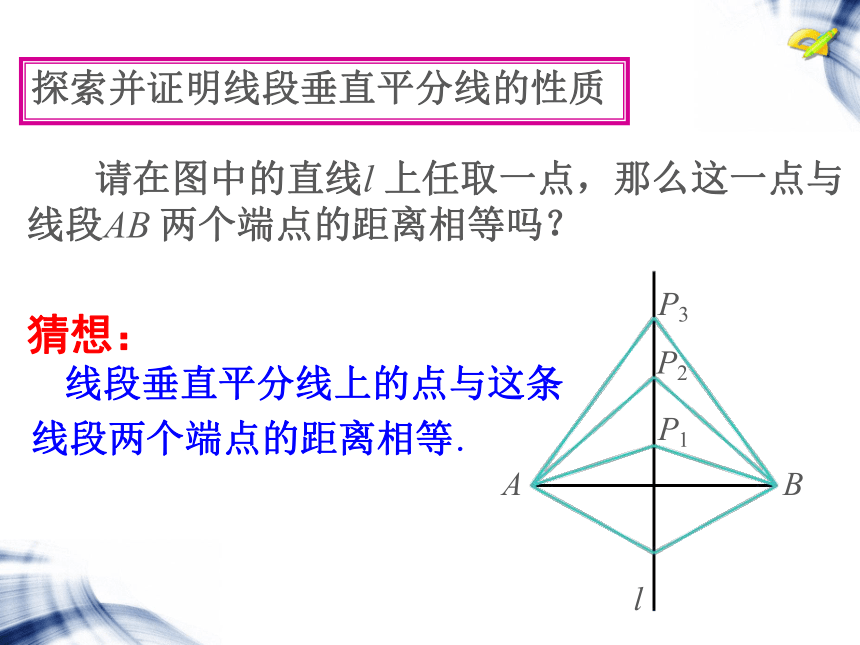
探索并证明线段垂直平分线的性质
请在图中的直线l
上任取一点,那么这一点与线段AB
两个端点的距离相等吗?
线段垂直平分线上的点与这条
线段两个端点的距离相等.
A
B
l
P1
P2
P3
猜想:
已知:如图,直线l⊥AB,垂足为C,AC
=CB,
点P
在l
上.
求证:PA
=PB.
探索并证明线段垂直平分线的性质
证明:“线段垂直平分线上的点到线段两端点的距
离相等.”
A
B
P
C
l
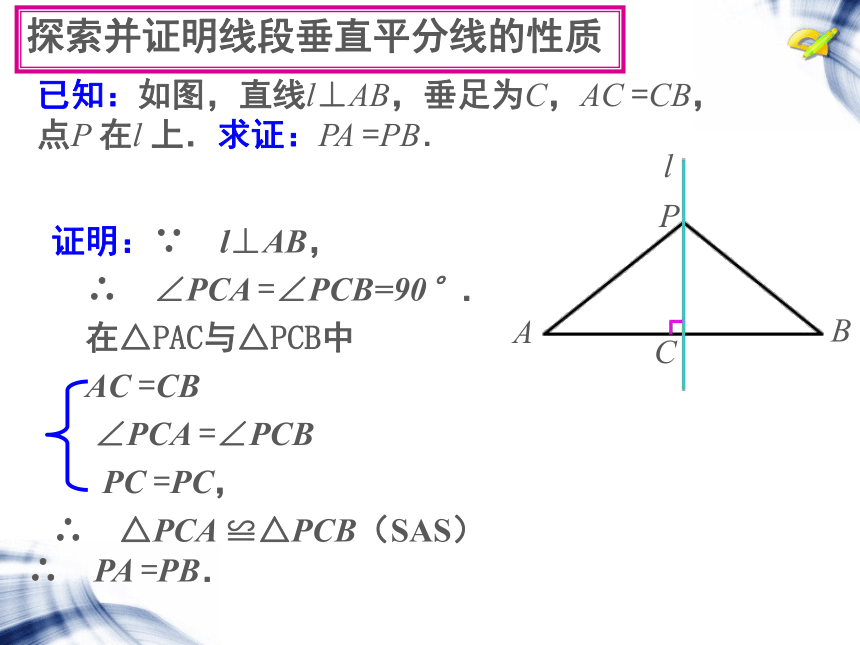
探索并证明线段垂直平分线的性质
证明:∵ l⊥AB,
∴
∠PCA
=∠PCB=90°.
在△PAC与△PCB中
AC
=CB
∠PCA
=∠PCB
PC
=PC,
∴
△PCA
≌△PCB(SAS)
∴
PA
=PB.
A
B
P
C
l
已知:如图,直线l⊥AB,垂足为C,AC
=CB,点P
在l
上.求证:PA
=PB.
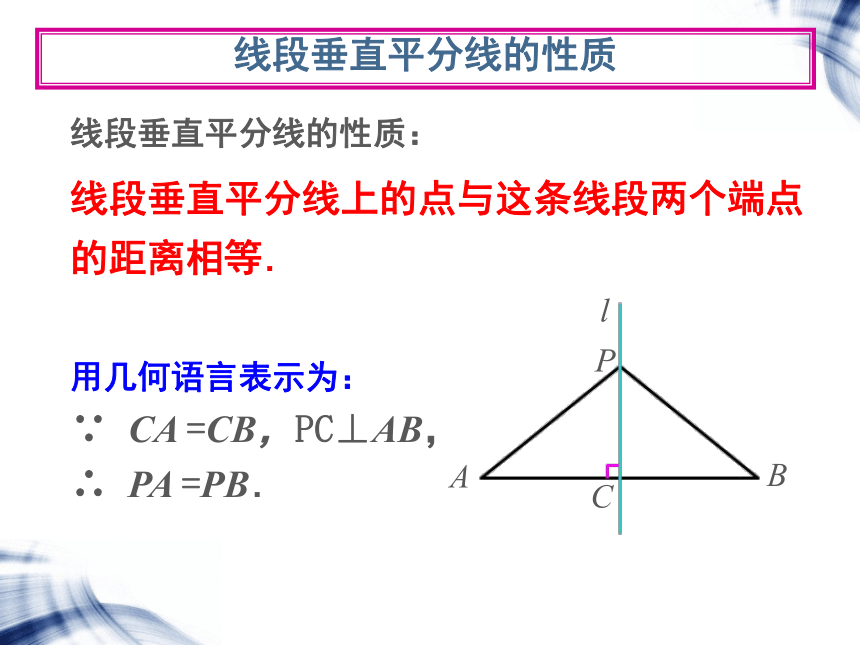
线段垂直平分线的性质
线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
A
B
P
C
l
用几何语言表示为:
∵
CA
=CB,PC⊥AB,
∴
PA
=PB.
例题讲解
1、
等腰△ABC中,AB=AC=20cm,DE垂直平分AB,
∠A
=50°
①已知AD=12.5cm,那么BD=
;
②已知△DBC的周长为35cm,则BC=
;
③若BC=13cm,则△DBC的周长为
;
④图中△
≌△
;
⑤∠EBD
=
°;
12.5cm
15cm
33cm
AED
BED
50
2、如图,AB=AC=8
cm,AB的垂直平分线交AC于D,若△ADB的周长为18,求DC的长.
◆[考点精练]
1、如图,在△ABC中,EF是AC的垂直平分线,
AF=12,BF=3,则BC为多少?
2、中考链接:如图,已知:△ABC中,BC<AC,AB边上的垂直平分线DE交AB于D,交AC于E,AC=9
cm,△BCE的周长为15
cm,求BC的长?
3.如图,直线AD是线段BC的垂直平分线.求证:∠ABD=∠ACD.
(1)本节课学习了哪些内容?
(2)线段垂直平分线的性质是什么?
(3)你是否能运用垂直平分线的性质进行解题?
课堂小结
布置作业
书本练习第1题.
导学案第45页
再见!
13.1.2线段的垂直平分线的性质(1)
授课人:林爱弟
学习目标:
1、探究线段垂直平分线的性质定理
2、经历探索线段垂直平分线的性质的过程,培养认真探究、积极思考的能力
重难点:线段垂直平分线的性质定理的应用
你能用不同的方法验证这一结论吗?
探索并证明线段垂直平分线的性质
如图,直线l
垂直平分线段AB,P1,P2,P3,…是
l
上的点,请猜想点P1,P2,P3,…
到点A
与点B
的距
离之间的数量关系.
相等.
A
B
l
P1
P2
P3
探索并证明线段垂直平分线的性质
请在图中的直线l
上任取一点,那么这一点与线段AB
两个端点的距离相等吗?
线段垂直平分线上的点与这条
线段两个端点的距离相等.
A
B
l
P1
P2
P3
猜想:
已知:如图,直线l⊥AB,垂足为C,AC
=CB,
点P
在l
上.
求证:PA
=PB.
探索并证明线段垂直平分线的性质
证明:“线段垂直平分线上的点到线段两端点的距
离相等.”
A
B
P
C
l
探索并证明线段垂直平分线的性质
证明:∵ l⊥AB,
∴
∠PCA
=∠PCB=90°.
在△PAC与△PCB中
AC
=CB
∠PCA
=∠PCB
PC
=PC,
∴
△PCA
≌△PCB(SAS)
∴
PA
=PB.
A
B
P
C
l
已知:如图,直线l⊥AB,垂足为C,AC
=CB,点P
在l
上.求证:PA
=PB.
线段垂直平分线的性质
线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
A
B
P
C
l
用几何语言表示为:
∵
CA
=CB,PC⊥AB,
∴
PA
=PB.
例题讲解
1、
等腰△ABC中,AB=AC=20cm,DE垂直平分AB,
∠A
=50°
①已知AD=12.5cm,那么BD=
;
②已知△DBC的周长为35cm,则BC=
;
③若BC=13cm,则△DBC的周长为
;
④图中△
≌△
;
⑤∠EBD
=
°;
12.5cm
15cm
33cm
AED
BED
50
2、如图,AB=AC=8
cm,AB的垂直平分线交AC于D,若△ADB的周长为18,求DC的长.
◆[考点精练]
1、如图,在△ABC中,EF是AC的垂直平分线,
AF=12,BF=3,则BC为多少?
2、中考链接:如图,已知:△ABC中,BC<AC,AB边上的垂直平分线DE交AB于D,交AC于E,AC=9
cm,△BCE的周长为15
cm,求BC的长?
3.如图,直线AD是线段BC的垂直平分线.求证:∠ABD=∠ACD.
(1)本节课学习了哪些内容?
(2)线段垂直平分线的性质是什么?
(3)你是否能运用垂直平分线的性质进行解题?
课堂小结
布置作业
书本练习第1题.
导学案第45页
再见!
