2020-2021学年北师大新版九年级下册数学《第3章 圆》单元测试卷(word版,有答案)
文档属性
| 名称 | 2020-2021学年北师大新版九年级下册数学《第3章 圆》单元测试卷(word版,有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 298.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 22:39:50 | ||
图片预览



文档简介
2020-2021学年北师大新版九年级下册数学《第3章
圆》单元测试卷
一.选择题
1.以已知点O为圆心,已知线段a为半径作圆,可以作( )
A.1个
B.2个
C.3个
D.无数个
2.半圆的圆心角( )
A.大于180°
B.等于180°
C.在90°~180°之间
D.等于90°
3.若P为半径长是6cm的⊙O内一点,OP=2cm,则过P点的最短的弦长为( )
A.12cm
B.
cm
C.
cm
D.
cm
4.如图,AB是⊙O的直径,AC是弦,若∠ACO=30°,则sin∠COB的等于( )
A.
B.
C.
D.
5.已知⊙O的半径为1,点P到O的距离为R,且方程x2﹣2x+R=0有实数根,则P( )
A.在⊙O的内部
B.在⊙O上
C.在⊙O外部
D.在⊙O的内部或圆上
6.已知△ABC面积为18cm2,BC=12cm,以A为圆心,BC边上的高为半径的圆与BC( )
A.相离
B.相切
C.相交
D.位置关系无法确定
7.如图,在等腰梯形ABCD中,AB∥DC,AB=21cm,CD=9cm,DA=10cm.⊙O1与OO2分别为△ABD和△BCD的内切圆,它们的半径分别为r1,r2,则的值是( )
A.
B.
C.
D.
8.下列命题中,真命题的个数为( )
①任意三点确定一个圆;②平分弦的直径垂直于弦;③90°的圆周角所对的弦是直径;④同弧或等弧所对的圆周角相等.
A.1个
B.2个
C.3个
D.4个
9.圆内接正方形的面积为a,则圆的面积为( )
A.2πa
B.
C.
D.以上都不对
10.已知,如图,在△ABC中,BC=2,AC=2,AB=4,以A为圆心,AC为半径画弧交AB于E,以B为圆心,BC为半径画弧交AB于F,则图中的阴影部分的面积是( )
A.
B.
C.
D.
二.填空题
11.如图所示,点M,N分别是正八边形相邻两边AB,BC上的点,且AM=BN,则∠MON=
度.
12.点A在以O为圆心,3cm为半径的⊙O内,则点A到圆心O的距离d的范围是
.
13.如图在⊙O中,直径AB⊥弦CD,垂足为P,∠BAD=30°,则∠AOC的度数是
度.
14.如图,A,B,C是⊙O上三点,当BC平分∠ABO时,能得出结论:
(任写一个).
15.为检测一种铁球的大小是否符合要求,设计一种工件槽,槽的两个底角均为90°,尺寸如图(单位:cm)若图中的铁球是合格的,请根据图中的数据求这个铁球的直径
cm.
16.现用总长为80m的建筑材料,围成一个扇形花坛,当扇形半径为
时,可使花坛的面积最大.
17.若一个直角三角形的斜边长为10,其内切圆半径为2,则这个三角形的周长是
.
18.在Rt△ABC,斜边AB=13cm,BC=12cm,以AB的中点O为圆心,2.5cm为半径画圆,则直线BC和⊙O的位置关系是
.
19.如图,△ABC内接于⊙O,∠C=30°,AB=4,连结OA,OB,则扇形OAB的面积为
.
20.如图,以点P为圆心的圆弧与x轴交于A,B两点,点P的坐标为(10,5),点A的坐标为(6,0),则点B的坐标为
.
三.解答题
21.如何在操场上画出一个很大的圆?说一说你的方法.作图说明:已知点AB=4cm,到点A的距离小于2cm,到点B的距离小于3cm的所有点组成的图形.
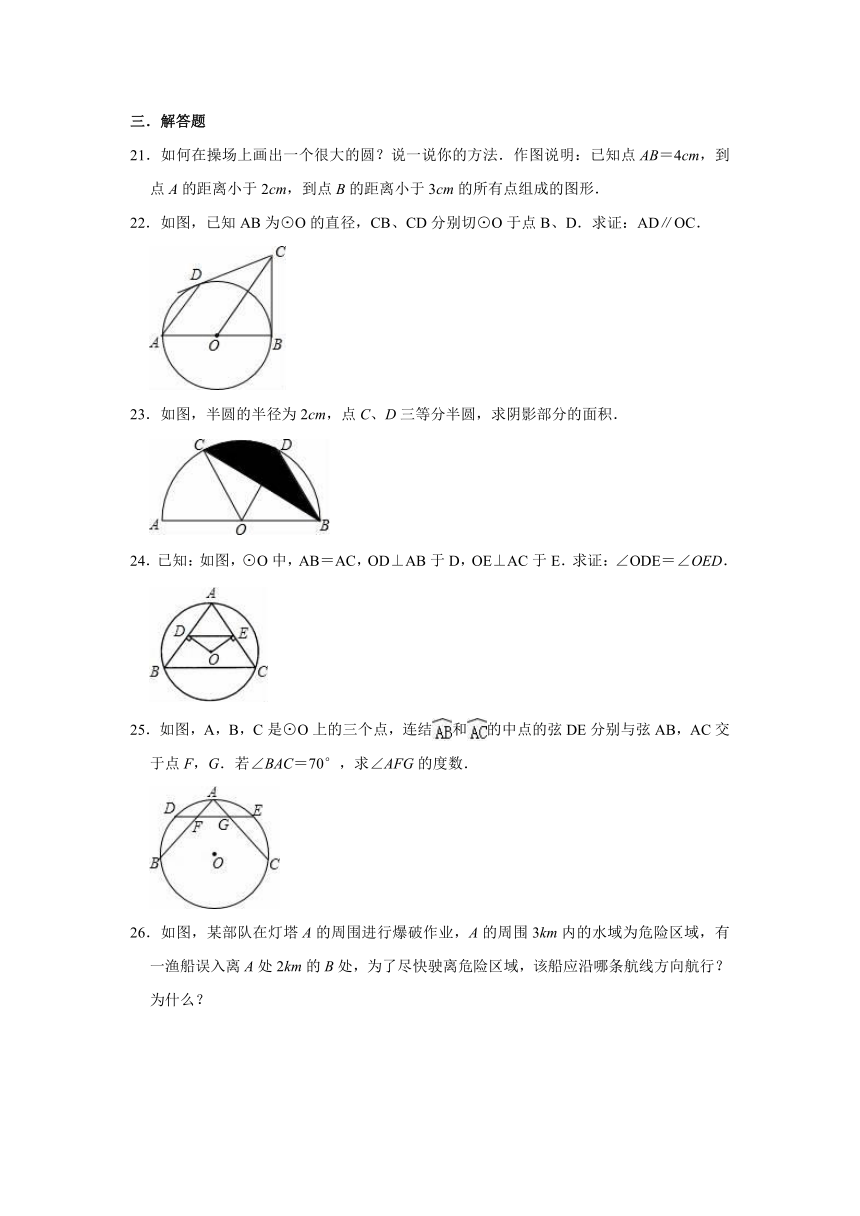
22.如图,已知AB为⊙O的直径,CB、CD分别切⊙O于点B、D.求证:AD∥OC.
23.如图,半圆的半径为2cm,点C、D三等分半圆,求阴影部分的面积.
24.已知:如图,⊙O中,AB=AC,OD⊥AB于D,OE⊥AC于E.求证:∠ODE=∠OED.
25.如图,A,B,C是⊙O上的三个点,连结和的中点的弦DE分别与弦AB,AC交于点F,G.若∠BAC=70°,求∠AFG的度数.
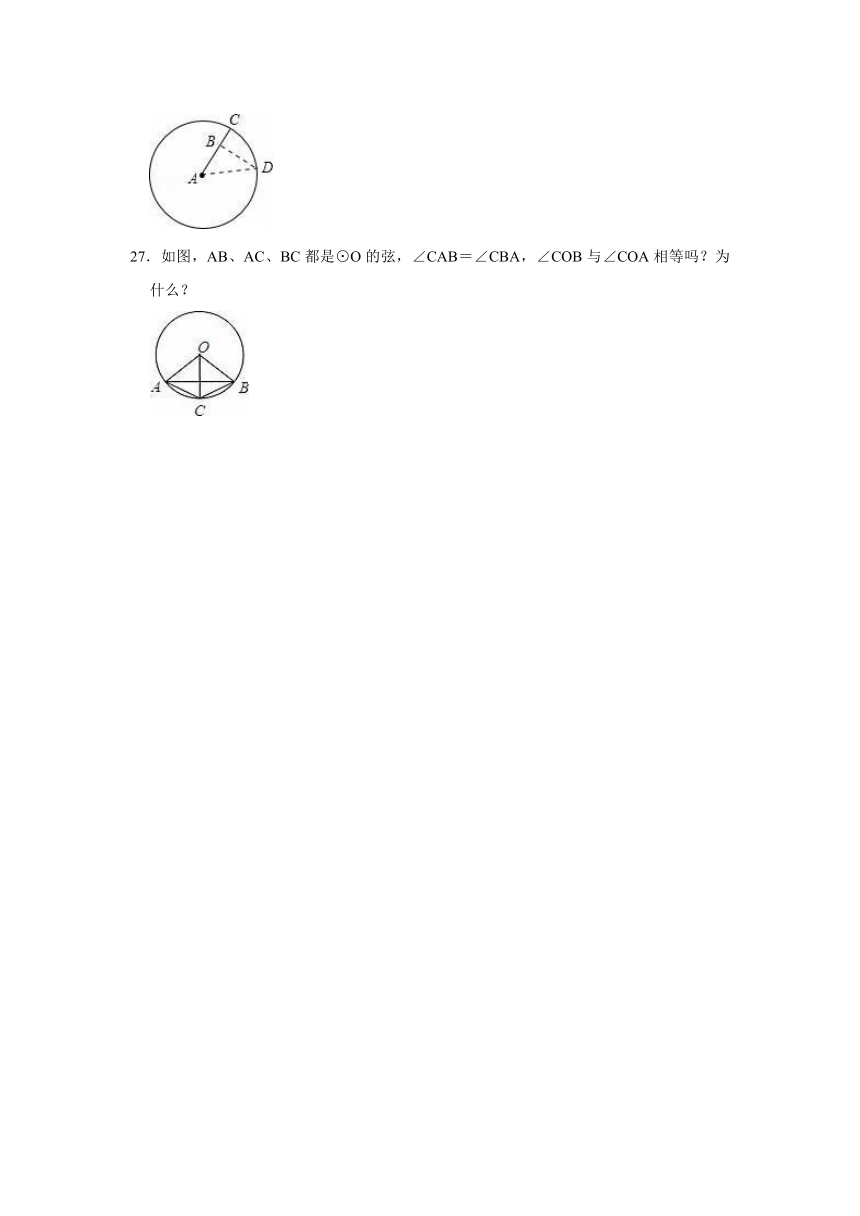
26.如图,某部队在灯塔A的周围进行爆破作业,A的周围3km内的水域为危险区域,有一渔船误入离A处2km的B处,为了尽快驶离危险区域,该船应沿哪条航线方向航行?为什么?
27.如图,AB、AC、BC都是⊙O的弦,∠CAB=∠CBA,∠COB与∠COA相等吗?为什么?
参考答案与试题解析
一.选择题
1.解:到定点距离等于定长的点只有一个,即以定点为圆心,定长为半径的圆.
故选:A.
2.解:∵半圆所对的弦是直径
∴半圆所对的圆心角是180度.
故选:B.
3.解:如图,∵OA=6cm,OP=2cm,
∴AP===4cm,
∴AB=8cm,
∴过P的最短的弦长等于8cm,
故选:D.
4.解:∵OA=OC,∠ACO=30°,
∴∠OAC=∠ACO=30°,
∵∠COB是△AOC的外角,
∴∠COB=∠ACO+∠OAC=60°,
∴sin∠COB=sin60°=.
故选:C.
5.解:因为方程有实数根,所以△=4﹣4R≥0,得到R≤1,
而圆的半径为1,说明点P到圆心的距离小于或等于半径,所以点P在圆内或圆上.
故选:D.
6.解:根据题意画出图形,如图所示:
以A为圆心,BC边上的高为半径,
则说明BC边上的高等于圆的半径,
∴该圆与BC相切.
故选:B.
7.解:过D作DE⊥AB于E,过C作CF⊥AB于F,则DE∥CF,
∵DC∥AB,
∴四边形DEFC是矩形,
∴DC=EF=9,DE=CF,
∵AD=BC.
在Rt△ADE和Rt△BCF中,AD=BC,DE=CF,
由勾股定理得:AE=BF=×(21﹣9)=6,
∴DE=CF==8,
在Rt△DEB中,由勾股定理得:BD==17,
在△DAB中,由三角形面积公式得:S△DAB=AB×DE=(AD+DB+AB)×r1,
∴×21×8=×(10+21+17)×r1,
解得r1=,
同理r2=2,
∴=,
故选:A.
8.解:①假命题,当三点在同一条直线上时,就不能确定一个圆了;
②假命题,当弦为直径时就不一定垂直了;
③真命题;
④真命题,同弧或等弧所对的圆周角相等.
故选:B.
9.解:∵圆内接正方形的面积为a,
则正方形的边长为,正方形的外接圆的半径为,
∴圆的面积为.
故选:B.
10.解:∵BC=2,AC=2,AB=4,
∴AB2=BC2+AC2,
∴△ABC为直角三角形,且∠C=90°,∠B=60°,∠A=30°,
S阴影部分=S扇形ACE+S扇形BCF﹣S△ABC,
∵S扇形ACE==π,
S扇形BCF==,
S△ABC=×2×2=2,
∴S阴影部分=π+﹣2=﹣2.
故选:C.
二.填空题
11.解:根据正八边形是中心对称图形可知:
∠MON=360°÷8=45°.
12.解:∵点A在以O为圆心,3cm为半径的⊙O内,
∴点A到圆心O的距离d的范围是:0≤d<3cm.
故答案为:0≤d<3cm.
13.解:∵∠BAD=30°,直径AB⊥弦CD,
∴∠D=90°﹣∠BAD=60°,
∴∠AOC=2∠D=120°.
故答案为:120.
14.解:∵A,B,C是⊙O上三点,当BC平分∠ABO时,
∴∠CBO=∠CBA.
∵OB=OC,
∴∠OCB=∠OBC.
∴∠CBA=∠OCB.
∴AB∥OC.
15.解:如图作辅助线;
由题意可设圆的半径为x厘米,OB=x﹣4,
∵△OAB为直角三角形
∴x2=82+(x﹣4)2
解得x=10厘米
所以这个铁球的直径为20厘米.
16.解:设扇形的半径为xm,则弧长为(80﹣2x)m,
根据题意有,S=?x?(80﹣2x)=﹣x2+40x,
∵a=﹣1<0,
∴S有最大值.
当x=﹣=20,S有最大值.
所以扇形半径为20m时,可使花坛的面积最大.
故答案为20m.
17.解:如图,
设AD=x,则BD=10﹣x,
∵⊙O是△ABC内切圆,
∴AD=AF=x,BD=BE=10﹣x,
∵∠C=∠OFC=∠OEC=90°,OE=OF,
∴四边形OECF为正方形,
∴CE=CF=2,
∴这个三角形周长:2x+2(10﹣x)+4=24.
故答案为:24.
18.解:过点O作OD⊥BC于点D,
∵∠C=90°,
∴OD∥AC,
∵O是AB的中点,
∴OD=AC,
如图,在Rt△ABC,斜边AB=13cm,BC=12cm,
∴AC==5(cm),
∴OD=2.5(cm),
∵以AB的中点O为圆心,2.5cm为半径画圆,
∴直线BC和⊙O的位置关系是:相切.
故答案为:相切.
19.解:∵∠AOB=2∠C=60°,OA=OB,
∴△OAB的等边三角形,
∴OA=OB=AB=4,
∴S扇形O﹣AB==π.
故答案为π.
20.解:过点P作PM⊥AB于M,则M的坐标是(10,0).
又∵A的坐标为(6,0),
∴OA=6,AM=OM﹣OA=10﹣6=4,
∵A,B两点一定关于PM对称.
∴MB=AM=4,
∴OB=OM+MB=10+4=14,
∴点B的坐标是(14,0).
故答案为:(14,0).
三.解答题
21.解:在操场上用一根很长的绳子,固定一头,拉紧后另一头旋转一周即可得到一个很大的圆.
阴影部分就是到点A的距离小于2cm,到点B的距离小于3cm的所有点组成的图形
22.证明:连接OD,
∵CB、CD分别切⊙O于点B、D,
∴CD=CB.
在△OBC与△ODC中,
∵
∴△OBC≌△ODC(SSS),
∴∠BOC=∠DOC,
∴=,
∴∠BOC=∠A,
∴AD∥OC.
23.解:如图,连接CD.
∵AB为半圆的直径,点C、D三等分半圆
∴∠AOC=∠COD=∠BOD=×180°=60°,
而OC=OD,
∴△OCD为等边三角形,
∴∠OCD=60°,
∴CD∥AB,
∴S△BCD=S△OCD,
∴S阴影=S扇形OCD==π(cm)2.
24.解:连接OA并延长交BC于点F,
∵⊙O是△ABC的外接圆,
∴点O是△ABC的外心,
∵AB=AC,
∴AF是BC的垂直平分线,
∴∠BAF=∠CAF,
∵OD⊥AB,OE⊥AC,
∴OD、OE分别是AB、AC的垂直平分线,
∵AB=AC,
∴AD=AE,
在Rt△AOD与Rt△AOE中,
,
∴Rt△AOD≌Rt△AOE,
∴OD=OE,
∴△ODE是等腰三角形,
∴∠ODE=∠OED.
25.解:连接OB、OC、OA、AD、OE、OF.
∵∠BOC=2∠BAC=140°,
∴∠AOB+∠AOC=360°﹣140°=220°,
又∵D、E是结和的中点,
∴∠BOD=∠AOB,∠AOE=∠AOC,
∴∠BOD+∠AOE=(∠AOB+∠AOC)=110°,
又∵∠DAB=∠BOD,∠ADF=∠AOE,
∴∠DAB+∠ADF=55°,
∴∠AFG=∠DAB+∠ADF=55°.
26.解:该船应沿航线AB方向航行离开危险区域.
理由如下:
如图,设航线AB交⊙A于点C,在⊙A上任取一点D(不包括C关于A的对称点)
连接AD、BD;
在△ABD中,
∵AB+BD>AD,AD=AC=AB+BC,
∴AB+BD>AB+BC,
∴BD>BC.
答:应沿AB的方向航行.
27.解:∠COB=∠COA,
理由是:∵∠CAB=∠CBA,∴AC=BC,
∴弧AC=弧BC,∴∠COB=∠COA.
圆》单元测试卷
一.选择题
1.以已知点O为圆心,已知线段a为半径作圆,可以作( )
A.1个
B.2个
C.3个
D.无数个
2.半圆的圆心角( )
A.大于180°
B.等于180°
C.在90°~180°之间
D.等于90°
3.若P为半径长是6cm的⊙O内一点,OP=2cm,则过P点的最短的弦长为( )
A.12cm
B.
cm
C.
cm
D.
cm
4.如图,AB是⊙O的直径,AC是弦,若∠ACO=30°,则sin∠COB的等于( )
A.
B.
C.
D.
5.已知⊙O的半径为1,点P到O的距离为R,且方程x2﹣2x+R=0有实数根,则P( )
A.在⊙O的内部
B.在⊙O上
C.在⊙O外部
D.在⊙O的内部或圆上
6.已知△ABC面积为18cm2,BC=12cm,以A为圆心,BC边上的高为半径的圆与BC( )
A.相离
B.相切
C.相交
D.位置关系无法确定
7.如图,在等腰梯形ABCD中,AB∥DC,AB=21cm,CD=9cm,DA=10cm.⊙O1与OO2分别为△ABD和△BCD的内切圆,它们的半径分别为r1,r2,则的值是( )
A.
B.
C.
D.
8.下列命题中,真命题的个数为( )
①任意三点确定一个圆;②平分弦的直径垂直于弦;③90°的圆周角所对的弦是直径;④同弧或等弧所对的圆周角相等.
A.1个
B.2个
C.3个
D.4个
9.圆内接正方形的面积为a,则圆的面积为( )
A.2πa
B.
C.
D.以上都不对
10.已知,如图,在△ABC中,BC=2,AC=2,AB=4,以A为圆心,AC为半径画弧交AB于E,以B为圆心,BC为半径画弧交AB于F,则图中的阴影部分的面积是( )
A.
B.
C.
D.
二.填空题
11.如图所示,点M,N分别是正八边形相邻两边AB,BC上的点,且AM=BN,则∠MON=
度.
12.点A在以O为圆心,3cm为半径的⊙O内,则点A到圆心O的距离d的范围是
.
13.如图在⊙O中,直径AB⊥弦CD,垂足为P,∠BAD=30°,则∠AOC的度数是
度.
14.如图,A,B,C是⊙O上三点,当BC平分∠ABO时,能得出结论:
(任写一个).
15.为检测一种铁球的大小是否符合要求,设计一种工件槽,槽的两个底角均为90°,尺寸如图(单位:cm)若图中的铁球是合格的,请根据图中的数据求这个铁球的直径
cm.
16.现用总长为80m的建筑材料,围成一个扇形花坛,当扇形半径为
时,可使花坛的面积最大.
17.若一个直角三角形的斜边长为10,其内切圆半径为2,则这个三角形的周长是
.
18.在Rt△ABC,斜边AB=13cm,BC=12cm,以AB的中点O为圆心,2.5cm为半径画圆,则直线BC和⊙O的位置关系是
.
19.如图,△ABC内接于⊙O,∠C=30°,AB=4,连结OA,OB,则扇形OAB的面积为
.
20.如图,以点P为圆心的圆弧与x轴交于A,B两点,点P的坐标为(10,5),点A的坐标为(6,0),则点B的坐标为
.
三.解答题
21.如何在操场上画出一个很大的圆?说一说你的方法.作图说明:已知点AB=4cm,到点A的距离小于2cm,到点B的距离小于3cm的所有点组成的图形.
22.如图,已知AB为⊙O的直径,CB、CD分别切⊙O于点B、D.求证:AD∥OC.
23.如图,半圆的半径为2cm,点C、D三等分半圆,求阴影部分的面积.
24.已知:如图,⊙O中,AB=AC,OD⊥AB于D,OE⊥AC于E.求证:∠ODE=∠OED.
25.如图,A,B,C是⊙O上的三个点,连结和的中点的弦DE分别与弦AB,AC交于点F,G.若∠BAC=70°,求∠AFG的度数.
26.如图,某部队在灯塔A的周围进行爆破作业,A的周围3km内的水域为危险区域,有一渔船误入离A处2km的B处,为了尽快驶离危险区域,该船应沿哪条航线方向航行?为什么?
27.如图,AB、AC、BC都是⊙O的弦,∠CAB=∠CBA,∠COB与∠COA相等吗?为什么?
参考答案与试题解析
一.选择题
1.解:到定点距离等于定长的点只有一个,即以定点为圆心,定长为半径的圆.
故选:A.
2.解:∵半圆所对的弦是直径
∴半圆所对的圆心角是180度.
故选:B.
3.解:如图,∵OA=6cm,OP=2cm,
∴AP===4cm,
∴AB=8cm,
∴过P的最短的弦长等于8cm,
故选:D.
4.解:∵OA=OC,∠ACO=30°,
∴∠OAC=∠ACO=30°,
∵∠COB是△AOC的外角,
∴∠COB=∠ACO+∠OAC=60°,
∴sin∠COB=sin60°=.
故选:C.
5.解:因为方程有实数根,所以△=4﹣4R≥0,得到R≤1,
而圆的半径为1,说明点P到圆心的距离小于或等于半径,所以点P在圆内或圆上.
故选:D.
6.解:根据题意画出图形,如图所示:
以A为圆心,BC边上的高为半径,
则说明BC边上的高等于圆的半径,
∴该圆与BC相切.
故选:B.
7.解:过D作DE⊥AB于E,过C作CF⊥AB于F,则DE∥CF,
∵DC∥AB,
∴四边形DEFC是矩形,
∴DC=EF=9,DE=CF,
∵AD=BC.
在Rt△ADE和Rt△BCF中,AD=BC,DE=CF,
由勾股定理得:AE=BF=×(21﹣9)=6,
∴DE=CF==8,
在Rt△DEB中,由勾股定理得:BD==17,
在△DAB中,由三角形面积公式得:S△DAB=AB×DE=(AD+DB+AB)×r1,
∴×21×8=×(10+21+17)×r1,
解得r1=,
同理r2=2,
∴=,
故选:A.
8.解:①假命题,当三点在同一条直线上时,就不能确定一个圆了;
②假命题,当弦为直径时就不一定垂直了;
③真命题;
④真命题,同弧或等弧所对的圆周角相等.
故选:B.
9.解:∵圆内接正方形的面积为a,
则正方形的边长为,正方形的外接圆的半径为,
∴圆的面积为.
故选:B.
10.解:∵BC=2,AC=2,AB=4,
∴AB2=BC2+AC2,
∴△ABC为直角三角形,且∠C=90°,∠B=60°,∠A=30°,
S阴影部分=S扇形ACE+S扇形BCF﹣S△ABC,
∵S扇形ACE==π,
S扇形BCF==,
S△ABC=×2×2=2,
∴S阴影部分=π+﹣2=﹣2.
故选:C.
二.填空题
11.解:根据正八边形是中心对称图形可知:
∠MON=360°÷8=45°.
12.解:∵点A在以O为圆心,3cm为半径的⊙O内,
∴点A到圆心O的距离d的范围是:0≤d<3cm.
故答案为:0≤d<3cm.
13.解:∵∠BAD=30°,直径AB⊥弦CD,
∴∠D=90°﹣∠BAD=60°,
∴∠AOC=2∠D=120°.
故答案为:120.
14.解:∵A,B,C是⊙O上三点,当BC平分∠ABO时,
∴∠CBO=∠CBA.
∵OB=OC,
∴∠OCB=∠OBC.
∴∠CBA=∠OCB.
∴AB∥OC.
15.解:如图作辅助线;
由题意可设圆的半径为x厘米,OB=x﹣4,
∵△OAB为直角三角形
∴x2=82+(x﹣4)2
解得x=10厘米
所以这个铁球的直径为20厘米.
16.解:设扇形的半径为xm,则弧长为(80﹣2x)m,
根据题意有,S=?x?(80﹣2x)=﹣x2+40x,
∵a=﹣1<0,
∴S有最大值.
当x=﹣=20,S有最大值.
所以扇形半径为20m时,可使花坛的面积最大.
故答案为20m.
17.解:如图,
设AD=x,则BD=10﹣x,
∵⊙O是△ABC内切圆,
∴AD=AF=x,BD=BE=10﹣x,
∵∠C=∠OFC=∠OEC=90°,OE=OF,
∴四边形OECF为正方形,
∴CE=CF=2,
∴这个三角形周长:2x+2(10﹣x)+4=24.
故答案为:24.
18.解:过点O作OD⊥BC于点D,
∵∠C=90°,
∴OD∥AC,
∵O是AB的中点,
∴OD=AC,
如图,在Rt△ABC,斜边AB=13cm,BC=12cm,
∴AC==5(cm),
∴OD=2.5(cm),
∵以AB的中点O为圆心,2.5cm为半径画圆,
∴直线BC和⊙O的位置关系是:相切.
故答案为:相切.
19.解:∵∠AOB=2∠C=60°,OA=OB,
∴△OAB的等边三角形,
∴OA=OB=AB=4,
∴S扇形O﹣AB==π.
故答案为π.
20.解:过点P作PM⊥AB于M,则M的坐标是(10,0).
又∵A的坐标为(6,0),
∴OA=6,AM=OM﹣OA=10﹣6=4,
∵A,B两点一定关于PM对称.
∴MB=AM=4,
∴OB=OM+MB=10+4=14,
∴点B的坐标是(14,0).
故答案为:(14,0).
三.解答题
21.解:在操场上用一根很长的绳子,固定一头,拉紧后另一头旋转一周即可得到一个很大的圆.
阴影部分就是到点A的距离小于2cm,到点B的距离小于3cm的所有点组成的图形
22.证明:连接OD,
∵CB、CD分别切⊙O于点B、D,
∴CD=CB.
在△OBC与△ODC中,
∵
∴△OBC≌△ODC(SSS),
∴∠BOC=∠DOC,
∴=,
∴∠BOC=∠A,
∴AD∥OC.
23.解:如图,连接CD.
∵AB为半圆的直径,点C、D三等分半圆
∴∠AOC=∠COD=∠BOD=×180°=60°,
而OC=OD,
∴△OCD为等边三角形,
∴∠OCD=60°,
∴CD∥AB,
∴S△BCD=S△OCD,
∴S阴影=S扇形OCD==π(cm)2.
24.解:连接OA并延长交BC于点F,
∵⊙O是△ABC的外接圆,
∴点O是△ABC的外心,
∵AB=AC,
∴AF是BC的垂直平分线,
∴∠BAF=∠CAF,
∵OD⊥AB,OE⊥AC,
∴OD、OE分别是AB、AC的垂直平分线,
∵AB=AC,
∴AD=AE,
在Rt△AOD与Rt△AOE中,
,
∴Rt△AOD≌Rt△AOE,
∴OD=OE,
∴△ODE是等腰三角形,
∴∠ODE=∠OED.
25.解:连接OB、OC、OA、AD、OE、OF.
∵∠BOC=2∠BAC=140°,
∴∠AOB+∠AOC=360°﹣140°=220°,
又∵D、E是结和的中点,
∴∠BOD=∠AOB,∠AOE=∠AOC,
∴∠BOD+∠AOE=(∠AOB+∠AOC)=110°,
又∵∠DAB=∠BOD,∠ADF=∠AOE,
∴∠DAB+∠ADF=55°,
∴∠AFG=∠DAB+∠ADF=55°.
26.解:该船应沿航线AB方向航行离开危险区域.
理由如下:
如图,设航线AB交⊙A于点C,在⊙A上任取一点D(不包括C关于A的对称点)
连接AD、BD;
在△ABD中,
∵AB+BD>AD,AD=AC=AB+BC,
∴AB+BD>AB+BC,
∴BD>BC.
答:应沿AB的方向航行.
27.解:∠COB=∠COA,
理由是:∵∠CAB=∠CBA,∴AC=BC,
∴弧AC=弧BC,∴∠COB=∠COA.
