青岛版八年级上第1章轴对称与轴对称图形复习学案
文档属性
| 名称 | 青岛版八年级上第1章轴对称与轴对称图形复习学案 |  | |
| 格式 | zip | ||
| 文件大小 | 30.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-14 18:48:28 | ||
图片预览

文档简介
八年级数学复习提纲(上)
第一章 轴对称和轴对称图形
[经验介绍]在学习中要养成练后反思的习惯,怎样做好反思呢?
(1)怎样做出来的?想解题所使用的方法
(2)为什么这样做?想解题所依据的原理
(3)为什么用这种方法?想解题的思路
(4)有无其他解法?哪种方法更好?一题多解
(5)能否变通一下而变成另一道习题?一题多变
(6)错解根源是什么?应注意哪些事项?如何克服?
[本章重点] 线段垂直平分线的性质,角平分线的性质,等腰三角形的性质,轴对称图形的性质。
[知识要点]1、轴对称图形的定义 。
2、我们学过的轴对称图形有 (有 条对称轴)、 (有 条对称轴)、
(有 条对称轴)、 (有 条对称轴)、 (有 条对称轴)、
(有 条对称轴)、 (有 条对称轴)、 (有 条对称轴)、
(有 条对称轴)、 (有 条对称轴)、 (有 条对称轴)、
(有 条对称轴)、 (有 条对称轴)、 (有 条对称轴)、
(有 条对称轴)、 (有 条对称轴)、 (有 条对称轴)。
3、轴对称的定义: ;
性质是: 。
4、轴对称图形与轴对称的主要区别是: ;
它们的联系是 。
5、垂直平分线的定义是: ;
其性质是 ;
如图1,作出线段AB的垂直平分线MN
6、角平分线的定义是
其性质是 。
如图2,作出∠AOB的角平分线OC
7、等腰三角形的性质有:
(1) ;
(2) ;
(3) ;
(4) 。
8、镜面对称分两种情况:其特点分别是 和 ,说出各自的解决方法。
[典型题目]
1.角是 图形,它的对称轴是 ;
2.等腰三角形是 图形,它的对称轴是 ;
3.正n边形有 条对称轴。
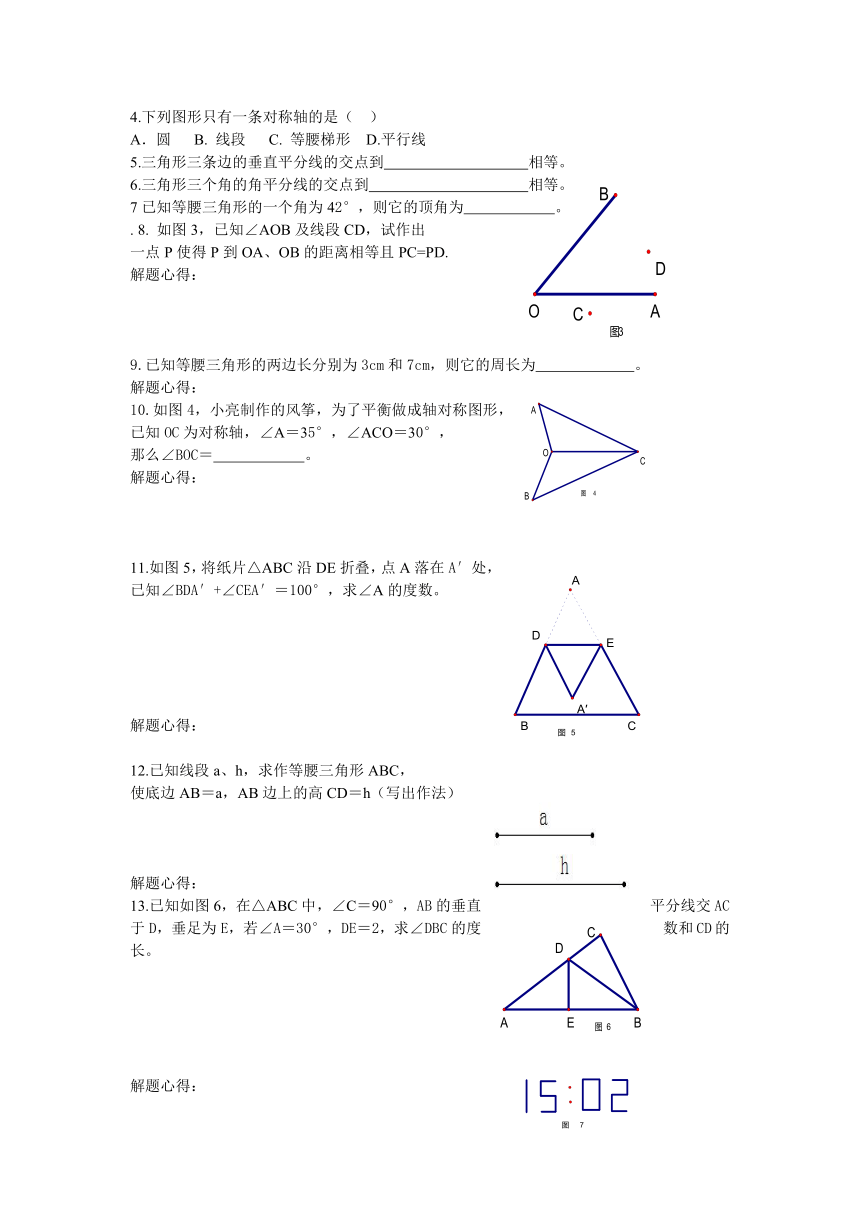
4.下列图形只有一条对称轴的是( )
A.圆 B. 线段 C. 等腰梯形 D.平行线
5.三角形三条边的垂直平分线的交点到 相等。
6.三角形三个角的角平分线的交点到 相等。
7已知等腰三角形的一个角为42°,则它的顶角为 。
. 8. 如图3,已知∠AOB及线段CD,试作出
一点P使得P到OA、OB的距离相等且PC=PD.
解题心得:
9.已知等腰三角形的两边长分别为3cm和7cm,则它的周长为 。
解题心得:
10.如图4,小亮制作的风筝,为了平衡做成轴对称图形,
已知OC为对称轴,∠A=35°,∠ACO=30°,
那么∠BOC= 。
解题心得:
11.如图5,将纸片△ABC沿DE折叠,点A落在A′处,
已知∠BDA′+∠CEA′=100°,求∠A的度数。
解题心得:
12.已知线段a、h,求作等腰三角形ABC,
使底边AB=a,AB边上的高CD=h(写出作法)
解题心得:
13.已知如图6,在△ABC中,∠C=90°,AB的垂直平分线交AC于D,垂足为E,若∠A=30°,DE=2,求∠DBC的度数和CD的长。
解题心得:
14.如图7,是小颖在平面镜里看到的对面墙壁上的电子
时钟的示数,这时的时间应该是 。
15.如图8,一辆汽车前面有一片积水,从水中看到的车牌号为
则实际是 。
解题心得:
16.如图9,点D是线段AB的中点,
CD⊥AB,DE⊥AC,DF⊥BC,求证:CE=CF。
解题心得:
[趣味数学]
假设一个池塘里面有无穷多的水,现有2 个空水壶容积分别是5升和6升,问题是如何只用这两个水壶从池塘里取得3升的水?
[挑战极限]
在△ABC中,AB>BC,BC的垂直平分线DE交△ABC的
外角平分线AD于D,DF⊥AB于F,
试说明BF-AC=AF
[学法总结]
1、把握数学概念的本质:(1)“轴对称图形”和“轴对称”的区别与联系是什么?
2、灵活运用图形的性质:
(1)当问题中出现中点、垂直的条件或要求线段相等时,要联想到线段垂直平分线的性质,
(2)当问题中出现角平分线的条件时或要求线段相等时,可以构造出到角两边的垂线段。
(3)当问题中要证明角相等、线段相等或两直线垂直时,要等腰三角形的“三线合一”。
(4)当问题中出现轴对称的图形时,要想想它的对应点、对应线段、对应角之间的关系。
3、数形结合的数学思想:数与形之间的相互转换,是数学的一种重要的数学思想方法。
4、尺规作图———基本作图:①作线段的垂直平分线 ②作角的平分线
组合作图:①作三角形 ②作轴对称图形
[错题分析] 在学习本章的过程中,我经常做错的题目和原因是
1、
2、
3、
[难点质疑]
我感到比较难的题有:
我不明白的问题还有:
第一章 轴对称和轴对称图形
[经验介绍]在学习中要养成练后反思的习惯,怎样做好反思呢?
(1)怎样做出来的?想解题所使用的方法
(2)为什么这样做?想解题所依据的原理
(3)为什么用这种方法?想解题的思路
(4)有无其他解法?哪种方法更好?一题多解
(5)能否变通一下而变成另一道习题?一题多变
(6)错解根源是什么?应注意哪些事项?如何克服?
[本章重点] 线段垂直平分线的性质,角平分线的性质,等腰三角形的性质,轴对称图形的性质。
[知识要点]1、轴对称图形的定义 。
2、我们学过的轴对称图形有 (有 条对称轴)、 (有 条对称轴)、
(有 条对称轴)、 (有 条对称轴)、 (有 条对称轴)、
(有 条对称轴)、 (有 条对称轴)、 (有 条对称轴)、
(有 条对称轴)、 (有 条对称轴)、 (有 条对称轴)、
(有 条对称轴)、 (有 条对称轴)、 (有 条对称轴)、
(有 条对称轴)、 (有 条对称轴)、 (有 条对称轴)。
3、轴对称的定义: ;
性质是: 。
4、轴对称图形与轴对称的主要区别是: ;
它们的联系是 。
5、垂直平分线的定义是: ;
其性质是 ;
如图1,作出线段AB的垂直平分线MN
6、角平分线的定义是
其性质是 。
如图2,作出∠AOB的角平分线OC
7、等腰三角形的性质有:
(1) ;
(2) ;
(3) ;
(4) 。
8、镜面对称分两种情况:其特点分别是 和 ,说出各自的解决方法。
[典型题目]
1.角是 图形,它的对称轴是 ;
2.等腰三角形是 图形,它的对称轴是 ;
3.正n边形有 条对称轴。
4.下列图形只有一条对称轴的是( )
A.圆 B. 线段 C. 等腰梯形 D.平行线
5.三角形三条边的垂直平分线的交点到 相等。
6.三角形三个角的角平分线的交点到 相等。
7已知等腰三角形的一个角为42°,则它的顶角为 。
. 8. 如图3,已知∠AOB及线段CD,试作出
一点P使得P到OA、OB的距离相等且PC=PD.
解题心得:
9.已知等腰三角形的两边长分别为3cm和7cm,则它的周长为 。
解题心得:
10.如图4,小亮制作的风筝,为了平衡做成轴对称图形,
已知OC为对称轴,∠A=35°,∠ACO=30°,
那么∠BOC= 。
解题心得:
11.如图5,将纸片△ABC沿DE折叠,点A落在A′处,
已知∠BDA′+∠CEA′=100°,求∠A的度数。
解题心得:
12.已知线段a、h,求作等腰三角形ABC,
使底边AB=a,AB边上的高CD=h(写出作法)
解题心得:
13.已知如图6,在△ABC中,∠C=90°,AB的垂直平分线交AC于D,垂足为E,若∠A=30°,DE=2,求∠DBC的度数和CD的长。
解题心得:
14.如图7,是小颖在平面镜里看到的对面墙壁上的电子
时钟的示数,这时的时间应该是 。
15.如图8,一辆汽车前面有一片积水,从水中看到的车牌号为
则实际是 。
解题心得:
16.如图9,点D是线段AB的中点,
CD⊥AB,DE⊥AC,DF⊥BC,求证:CE=CF。
解题心得:
[趣味数学]
假设一个池塘里面有无穷多的水,现有2 个空水壶容积分别是5升和6升,问题是如何只用这两个水壶从池塘里取得3升的水?
[挑战极限]
在△ABC中,AB>BC,BC的垂直平分线DE交△ABC的
外角平分线AD于D,DF⊥AB于F,
试说明BF-AC=AF
[学法总结]
1、把握数学概念的本质:(1)“轴对称图形”和“轴对称”的区别与联系是什么?
2、灵活运用图形的性质:
(1)当问题中出现中点、垂直的条件或要求线段相等时,要联想到线段垂直平分线的性质,
(2)当问题中出现角平分线的条件时或要求线段相等时,可以构造出到角两边的垂线段。
(3)当问题中要证明角相等、线段相等或两直线垂直时,要等腰三角形的“三线合一”。
(4)当问题中出现轴对称的图形时,要想想它的对应点、对应线段、对应角之间的关系。
3、数形结合的数学思想:数与形之间的相互转换,是数学的一种重要的数学思想方法。
4、尺规作图———基本作图:①作线段的垂直平分线 ②作角的平分线
组合作图:①作三角形 ②作轴对称图形
[错题分析] 在学习本章的过程中,我经常做错的题目和原因是
1、
2、
3、
[难点质疑]
我感到比较难的题有:
我不明白的问题还有:
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
