北师大版九年级数学下册 3.3 垂径定理 同步测试题(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学下册 3.3 垂径定理 同步测试题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 227.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 00:55:30 | ||
图片预览



文档简介
10617200107442001231900003.3 垂径定理 同步测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
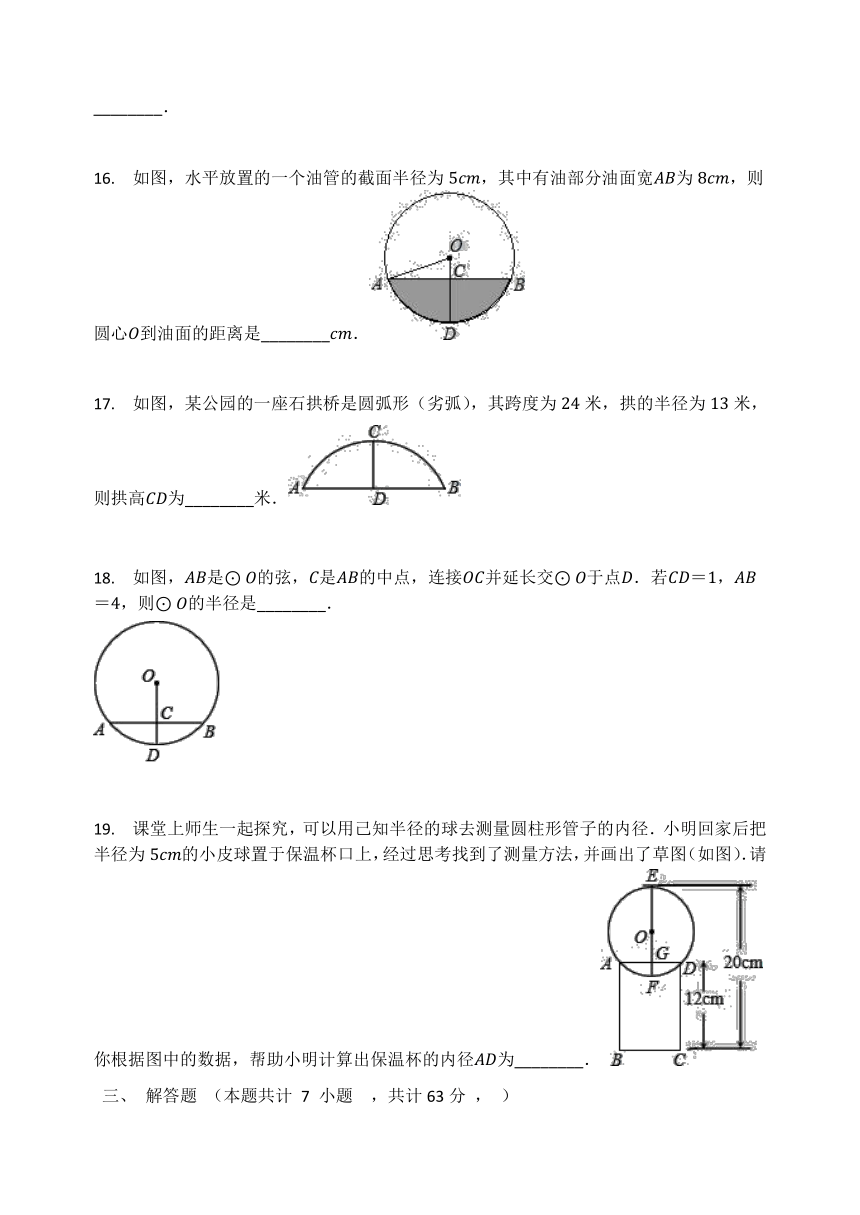
?1. 如图,在⊙O中,弦AB与直径CD垂直,垂足为E,则下列结论中错误的是( )
A.AE=BE B.CE=DE C.弧AC=弧BC D.弧AD=弧BD
?
2. 如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=73,则线段DN的长为( )
A.34 B.43 C.1 D.2
?
3. ⊙O的半径为10cm,两平行弦AC,BD的长分别为12cm,16cm,则两弦间的距离是( )
A.2cm B.14cm C.6cm或8cm D.2cm或14cm
?
4. AB是⊙O直径,弦CD⊥AB于点E.若CD=6,OE=4,则⊙O的直径为( )
A.5 B.6 C.8 D.10
?
5. 如图是某石圆弧形(劣弧)拱桥,其中跨度AB=24米,拱高CD=8米,则该圆弧的半径r=( )
A.8?米 B.12?米 C.13米 D.15?米
?
6. 若小唐同学掷出的铅球在场地上砸出一个直径约为10?cm、深约为2?cm的小坑,则该铅球的直径约为
( )
A.10cm B.14.5cm C.19.5cm D.20cm
?
7. 如图,已知AB为⊙O的直径,点B为CD的中点,则下列结论中一定正确的是( )
A.BM=OM B.AB⊥CD C.OM=12OC D.∠BOC=60?
?
8. 如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.∠C=12∠BOD B.AC=AB C.∠C=∠B D.∠A=∠BOD
?
9. 已知⊙O的半径为2,点P是⊙O内一点,且OP=3,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4 B.5 C.6 D.7
?
10. 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=12米,净高CD=9米,则此圆的半径OA=( )
A.122米 B.132米 C.142米 D.152米
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
11. 如图是某风景区的一个圆拱形门,路面AB宽为2m,净高CD为5m,则圆拱形门所在圆的半径为________m.
?
12. 如图,P是⊙O内一定点,请你在⊙O内作出过P点的最长弦和最短弦,标上字母,并指出最长弦是________,最短弦是________.
?
13. 已知⊙O的半径为6cm,P是⊙O内一点,OP=2cm,那么过P的最短的弦长等于________cm,过P的最长的弦长为________cm.
?
14. 已知:⊙O中的半径为4cm,弦AB所对的劣弧为圆的13,则弦AB的长为________cm,AB的弦心距为________cm.
?
15. 已知圆O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,则圆O的直径是________.
?
16. 如图,水平放置的一个油管的截面半径为5cm,其中有油部分油面宽AB为8cm,则圆心O到油面的距离是________cm.
?
17. 如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高CD为________米.
?
18. 如图,AB是⊙O的弦,C是AB的中点,连接OC并延长交⊙O于点D.若CD=1,AB=4,则⊙O的半径是________.
?
19. 课堂上师生一起探究,可以用己知半径的球去测量圆柱形管子的内径.小明回家后把半径为5cm的小皮球置于保温杯口上,经过思考找到了测量方法,并画出了草图(如图).请你根据图中的数据,帮助小明计算出保温杯的内径AD为________.
三、 解答题 (本题共计 7 小题 ,共计63分 , ) ?
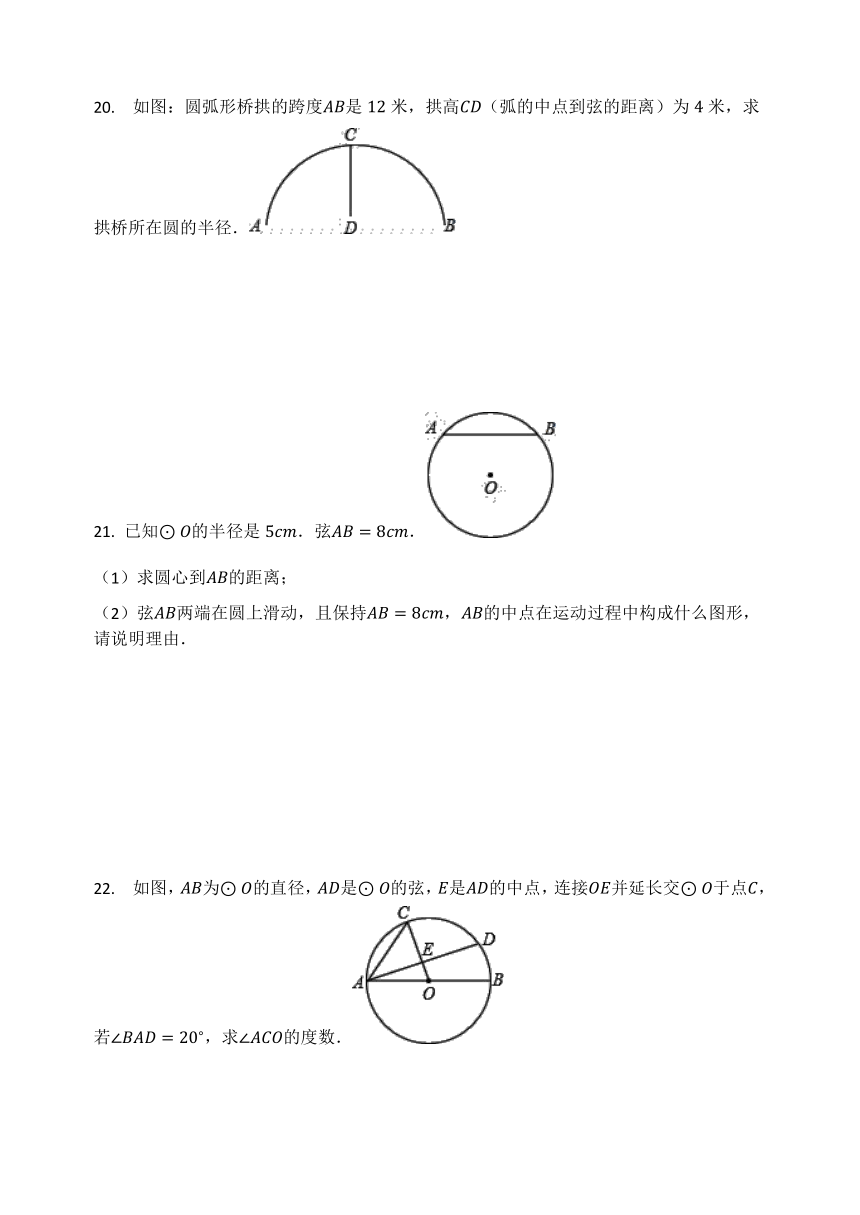
20. 如图:圆弧形桥拱的跨度AB是12米,拱高CD(弧的中点到弦的距离)为4米,求拱桥所在圆的半径.
?
21. 已知⊙O的半径是5cm.弦AB=8cm.
(1)求圆心到AB的距离;
(2)弦AB两端在圆上滑动,且保持AB=8cm,AB的中点在运动过程中构成什么图形,请说明理由.
?
22. 如图,AB为⊙O的直径,AD是⊙O的弦,E是AD的中点,连接OE并延长交⊙O于点C,若∠BAD=20?,求∠ACO的度数.
?
23. 如图,破残的圆形轮片上,弦AB的垂直平分线交AB于C,交弦AB于D,
(1)求作此残片所在的圆的圆心(不写作法,保留作图痕迹);
(2)若AB=8cm,CD=2cm,求(1)中所作圆的半径.
?
24. 已知:如图,在⊙O中,CD为弦,A、B两点在CD的两端延长线上,且AC=BD.
求证:△OAB为等腰三角形.
?
25. 如图,AB、CD是⊙O的弦,M、N分别为AB、CD的中点,且∠AMN=∠CNM.求证:AB=CD.
?
26. 如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.6m,
(1)求排水管内水的深度.
(2)当水面的宽AB为0.8m时,此时水面上升了多少米?
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
【解答】
解:∵ CD⊥AB,CD为直径,
∴ AE=BE,弧AD=弧BD,弧AC=弧BC,
CE>DE,
故选B.
2.
【答案】
B
【解答】
证明:作OH⊥CD于H,
则CH=DH=12CD=52,
∵ BF⊥CD,
∴ OH?//?AM,
而OA=OB,
∴ HM=HN=12MN=76,
∴ DN=DH-NH=52-76=43,
故选B.
3.
【答案】
D
【解答】
解:如图①
作OE⊥AC垂足为E,交BD于点F,
∵ OE⊥AC??AC?//?BD,
∴ OF⊥BD,
∴ AE=12AC=6cm?????BF=12BD=8cm,
在Rt△AOE中
OE=OA2-AE2=102-62=8cm
同理可得:
OF=6cm
∴ EF=OE-OF=8-6=2cm;
如图②
同理可得:EF=OE+OF=8+6=14cm
综上所述两弦之间的距离为2cm或14cm.
故选D.
4.
【答案】
D
【解答】
连接OC;
在Rt△OCE中,由垂径定理知CE=DE=3,
由勾股定理得:
OC2=OE2+CE2=32+42=52,即OC=5,
所以⊙O的直径为10,
5.
【答案】
C
【解答】
解:拱桥的跨度AB=24m,拱高CD=8m,
∴ AD=12m,
利用勾股定理可得:122=AO2-(AO-8)2,
解得AO=13m.
即圆弧半径为13米.
故选C.
6.
【答案】
B
【解答】
解:设该铅球的半径是r.
在由铅球的半径、小坑的半径即半弦和弦心距组成的直角三角形中,
根据勾股定理,得r2=(r-2)2+25,
解得r=7.25,∴ 2r=14.5.
故选B.
7.
【答案】
B
【解答】
解:A、无法判定BM=OM,故本选项错误;
B、∵ AB为⊙O的直径,B为CD的中点,∴ AB⊥CD,故本选项正确;
C、当点M为OC的中点时,OM=12OC,故本选项错误;
D、无法判定∠BOC=60?,故本选项错误.
故选B.
8.
【答案】
A
【解答】
解:连接AO,如图:
由垂径定理,得
AE=BE.
在△AEO和△BEO中,
AE=BE∠AEO=BEOOE=OE,
∴ △AEO?△BEO(SAS),
∴ ∠AOD=∠BOD.
由圆周角定理,得
∠C=12∠AOD.
由等量代换,得
∠C=12∠BOD,故A正确.
故选:A.
9.
【答案】
B
【解答】
解:如图:
连接OA、OD,作OE⊥AC,OF⊥BD,垂足分别为E、F,
∵ AC⊥BD,
∴ 四边形OEPF为矩形,
已知OA=OC=2,OP=3,
设OE为x,则OF=EP=OP2-OE2=3-x2,
∴ AC=2AE=2OA2-OE2=24-x2,
BD=2DF=2OD2-OF2=2x2+1,
如设OF为y,同理可得:
AC=2y2+1,BD=24-y2,
∴ AC2+BD2=20,
由此可知AC与BD两线段的平方和为定值,
又∵ 任意对角线互相垂直的四边形的面积等于对角线乘积的12,
当AC=BD时,即y2+1=4-y2,
y=62,
AC=BD=10,
∴ 四边形ABCD的面积等于5.
故选:B.
10.
【答案】
B
【解答】
解:设此圆的半径为r,则OA=r,OD=9-r,
∵ AB=12米,CD⊥AB,
∴ AD=12AB=12×12=6米,、
在Rt△AOD中,
∵ OA=r,OD=9-r,AD=6米,、
∴ OA2=OD2+AD2,即r2=(9-r)2+62,
解得r=132米.
故选B.
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
11.
【答案】
2.6
【解答】
解:连接OA;
Rt△OAD中,AD=12AB=1米;
设⊙O的半径为R,则OA=OC=R,OD=5-R;
由勾股定理,得:OA2=AD2+OD2,即:
R2=(5-R)2+12,解得R=2.6(米);
故答案为:2.6.
12.
【答案】
AB,CD
【解答】
解:最长的弦:AB
最短的弦:CD
故答案为:AB、CD.
13.
【答案】
82,12
【解答】
解:如图,
∵ OA=6cm,OP=2cm,∴ 由勾股定理得,AP=42cm,
∴ AB=82cm,
∴ 过P的最短的弦长等于82cm,
故答案为82;12.
14.
【答案】
2,43
【解答】
解:如图,
∵ 弦AB所对的劣弧为圆的13,
∴ ∠AOB=13×360?=120?.
∵ OC⊥AB,OA=OB,
∴ AC=CB,∠OAC=30?,
∴ OC=12OA=2,AC=OA?sin60?=4×32=23,
∴ AB=2AC=43.
故答案为:2,43.
15.
【答案】
10cm
【解答】
解:如图,∵ AB=8cm,OC=3cm,且OC⊥AB,
∴ BC=12AB=4cm,
连接OB,则OB=OC2+BC2=5cm.
∴ 圆O的直径是10cm.
故答案为:10cm.
16.
【答案】
3
【解答】
解:∵ OD⊥AB于C,
∴ AC=12AB=4cm.
在直角三角形AOC中,根据勾股定理,得
OC=OA2-AC2=3(cm).
17.
【答案】
8
【解答】
解:因为跨度AB=24m,拱所在圆半径为13m,
延长CD到O,使得OC=OA,则O为圆心,
则AD=12AB=12(米),
则OA=13米,
在Rt△AOD中,DO=OA2-AD2=5,
进而得拱高CD=CO-DO=13-5=8米.
故答案为:8.
18.
【答案】
52
【解答】
连接OA,
∵ C是AB的中点,
∴ AC=12AB=2,OC⊥AB,
∴ OA2=OC2+AC2,即OA2=(OA-1)2+22,
解得,OA=52,
19.
【答案】
8cm
【解答】
解:连OD.
∵ EG=20-12=8,
∴ OG=8-5=3,
∴ GD=4,
∴ AD=2GD=8cm.
故答案为8cm.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
20.
【答案】
解:如图,设圆的半径为R米,
∵ CD平分弧AB,且CD⊥AB,
∴ 圆心O在CD的延长线上,
∴ CD平分AB,
∴ AD=12AB=6,
连OA,
在Rt△OAD中,AD=6,OA=R,OD=R-CD=R-4,
∵ OA2=OD2+AD2,
∴ R2=62+(R-4)2,
解得R=132,
即拱桥所在圆的半径132米.
【解答】
解:如图,设圆的半径为R米,
∵ CD平分弧AB,且CD⊥AB,
∴ 圆心O在CD的延长线上,
∴ CD平分AB,
∴ AD=12AB=6,
连OA,
在Rt△OAD中,AD=6,OA=R,OD=R-CD=R-4,
∵ OA2=OD2+AD2,
∴ R2=62+(R-4)2,
解得R=132,
即拱桥所在圆的半径132米.
21.
【答案】
解:连接OB,作OD⊥AB于D.OD就是圆心O到弦AB的距离.
在⊙O中,∵ OD⊥AB
∴ D是弦AB的中点
在Rt△OBD中,OB=5,DB=12AB=4
OD=OB2-DB2=3
圆心O到弦AB的距离为3.
(2)由(1)知:D是弦AB的中点
AB中点D在运动过程中始终保持OD=3
∴ 据圆的定义,在AB运动过程中,点D运动的轨迹是以O为圆心,3为半径的圆.
【解答】
解:连接OB,作OD⊥AB于D.OD就是圆心O到弦AB的距离.
在⊙O中,∵ OD⊥AB
∴ D是弦AB的中点
在Rt△OBD中,OB=5,DB=12AB=4
OD=OB2-DB2=3
圆心O到弦AB的距离为3.
(2)由(1)知:D是弦AB的中点
AB中点D在运动过程中始终保持OD=3
∴ 据圆的定义,在AB运动过程中,点D运动的轨迹是以O为圆心,3为半径的圆.
22.
【答案】
解:∵ E是AD的中点,
∴ OE⊥AD,
∴ ∠AEO=90?,
∵ ∠BAD=20?,
∴ ∠AOE=70?,
∵ OA=OC,
∴ ∠OAC=∠AOC,
∴ ∠AOC=12(180?-∠AOC)=12(180?-70?)=55?.
【解答】
解:∵ E是AD的中点,
∴ OE⊥AD,
∴ ∠AEO=90?,
∵ ∠BAD=20?,
∴ ∠AOE=70?,
∵ OA=OC,
∴ ∠OAC=∠AOC,
∴ ∠AOC=12(180?-∠AOC)=12(180?-70?)=55?.
23.
【答案】
解:(1)
M就是所求的圆的圆心;
(2)设圆的半径是r.在直角△ADM中,AM=r,AD=4,DM=r-2.
根据勾股定理即可得到:r2=42+(r-2)2解得:r=5.
即圆的半径为5cm.
【解答】
解:(1)
M就是所求的圆的圆心;
(2)设圆的半径是r.在直角△ADM中,AM=r,AD=4,DM=r-2.
根据勾股定理即可得到:r2=42+(r-2)2解得:r=5.
即圆的半径为5cm.
24.
【答案】
证明:过O作OE⊥CD于E,
∵ OE⊥CD,
∴ CE=DE.
∵ AC=BD,
∴ AC+CE=BD+DE.
∴ AE=BE.
∴ OA=OB.
∴ △OAB为等腰三角形.
【解答】
证明:过O作OE⊥CD于E,
∵ OE⊥CD,
∴ CE=DE.
∵ AC=BD,
∴ AC+CE=BD+DE.
∴ AE=BE.
∴ OA=OB.
∴ △OAB为等腰三角形.
25.
【答案】
证明:连接OM,ON,OA,OC,
∵ M、N分别为AB、CD的中点,
∴ OM⊥AB,ON⊥CD,
∴ AM=12AB,CN=12CD,
∵ ∠AMN=∠CNM,
∴ ∠NMO=∠MNO,即OM=ON,
在Rt△AOM与Rt△CON中,
∵ OM=ONOA=OC,
∴ Rt△AOM?Rt△CON(HL),
∴ AM=CN,
∴ AB=CD.
【解答】
证明:连接OM,ON,OA,OC,
∵ M、N分别为AB、CD的中点,
∴ OM⊥AB,ON⊥CD,
∴ AM=12AB,CN=12CD,
∵ ∠AMN=∠CNM,
∴ ∠NMO=∠MNO,即OM=ON,
在Rt△AOM与Rt△CON中,
∵ OM=ONOA=OC,
∴ Rt△AOM?Rt△CON(HL),
∴ AM=CN,
∴ AB=CD.
26.
【答案】
解:(1)作半径OC⊥AB,垂足为点D,连接OA,则CD即为弓形高,
∵ OC⊥AB,
∴ AD=12AB,
∵ AO=0.5,AB=0.6,
∴ AD=12AB=12×0.6=0.3,
∴ OD=AO2-AD2=0.4,
∴ CD=OC-OD=0.5-0.4=0.1米,即此时的水深为0.1米
(2)当水位上升到水面宽MN为0.8米时,直线OC与MN相交于点P
同理可得OP=0.3,
当MN与AB在圆心同侧时,水面上升的高度为0.1米;
当MN与AB在圆心异侧时,水面上升的高度为0.7米.
【解答】
解:(1)作半径OC⊥AB,垂足为点D,连接OA,则CD即为弓形高,
∵ OC⊥AB,
∴ AD=12AB,
∵ AO=0.5,AB=0.6,
∴ AD=12AB=12×0.6=0.3,
∴ OD=AO2-AD2=0.4,
∴ CD=OC-OD=0.5-0.4=0.1米,即此时的水深为0.1米
(2)当水位上升到水面宽MN为0.8米时,直线OC与MN相交于点P
同理可得OP=0.3,
当MN与AB在圆心同侧时,水面上升的高度为0.1米;
当MN与AB在圆心异侧时,水面上升的高度为0.7米.
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 如图,在⊙O中,弦AB与直径CD垂直,垂足为E,则下列结论中错误的是( )
A.AE=BE B.CE=DE C.弧AC=弧BC D.弧AD=弧BD
?
2. 如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=73,则线段DN的长为( )
A.34 B.43 C.1 D.2
?
3. ⊙O的半径为10cm,两平行弦AC,BD的长分别为12cm,16cm,则两弦间的距离是( )
A.2cm B.14cm C.6cm或8cm D.2cm或14cm
?
4. AB是⊙O直径,弦CD⊥AB于点E.若CD=6,OE=4,则⊙O的直径为( )
A.5 B.6 C.8 D.10
?
5. 如图是某石圆弧形(劣弧)拱桥,其中跨度AB=24米,拱高CD=8米,则该圆弧的半径r=( )
A.8?米 B.12?米 C.13米 D.15?米
?
6. 若小唐同学掷出的铅球在场地上砸出一个直径约为10?cm、深约为2?cm的小坑,则该铅球的直径约为
( )
A.10cm B.14.5cm C.19.5cm D.20cm
?
7. 如图,已知AB为⊙O的直径,点B为CD的中点,则下列结论中一定正确的是( )
A.BM=OM B.AB⊥CD C.OM=12OC D.∠BOC=60?
?
8. 如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.∠C=12∠BOD B.AC=AB C.∠C=∠B D.∠A=∠BOD
?
9. 已知⊙O的半径为2,点P是⊙O内一点,且OP=3,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4 B.5 C.6 D.7
?
10. 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=12米,净高CD=9米,则此圆的半径OA=( )
A.122米 B.132米 C.142米 D.152米
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
11. 如图是某风景区的一个圆拱形门,路面AB宽为2m,净高CD为5m,则圆拱形门所在圆的半径为________m.
?
12. 如图,P是⊙O内一定点,请你在⊙O内作出过P点的最长弦和最短弦,标上字母,并指出最长弦是________,最短弦是________.
?
13. 已知⊙O的半径为6cm,P是⊙O内一点,OP=2cm,那么过P的最短的弦长等于________cm,过P的最长的弦长为________cm.
?
14. 已知:⊙O中的半径为4cm,弦AB所对的劣弧为圆的13,则弦AB的长为________cm,AB的弦心距为________cm.
?
15. 已知圆O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,则圆O的直径是________.
?
16. 如图,水平放置的一个油管的截面半径为5cm,其中有油部分油面宽AB为8cm,则圆心O到油面的距离是________cm.
?
17. 如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高CD为________米.
?
18. 如图,AB是⊙O的弦,C是AB的中点,连接OC并延长交⊙O于点D.若CD=1,AB=4,则⊙O的半径是________.
?
19. 课堂上师生一起探究,可以用己知半径的球去测量圆柱形管子的内径.小明回家后把半径为5cm的小皮球置于保温杯口上,经过思考找到了测量方法,并画出了草图(如图).请你根据图中的数据,帮助小明计算出保温杯的内径AD为________.
三、 解答题 (本题共计 7 小题 ,共计63分 , ) ?
20. 如图:圆弧形桥拱的跨度AB是12米,拱高CD(弧的中点到弦的距离)为4米,求拱桥所在圆的半径.
?
21. 已知⊙O的半径是5cm.弦AB=8cm.
(1)求圆心到AB的距离;
(2)弦AB两端在圆上滑动,且保持AB=8cm,AB的中点在运动过程中构成什么图形,请说明理由.
?
22. 如图,AB为⊙O的直径,AD是⊙O的弦,E是AD的中点,连接OE并延长交⊙O于点C,若∠BAD=20?,求∠ACO的度数.
?
23. 如图,破残的圆形轮片上,弦AB的垂直平分线交AB于C,交弦AB于D,
(1)求作此残片所在的圆的圆心(不写作法,保留作图痕迹);
(2)若AB=8cm,CD=2cm,求(1)中所作圆的半径.
?
24. 已知:如图,在⊙O中,CD为弦,A、B两点在CD的两端延长线上,且AC=BD.
求证:△OAB为等腰三角形.
?
25. 如图,AB、CD是⊙O的弦,M、N分别为AB、CD的中点,且∠AMN=∠CNM.求证:AB=CD.
?
26. 如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.6m,
(1)求排水管内水的深度.
(2)当水面的宽AB为0.8m时,此时水面上升了多少米?
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
【解答】
解:∵ CD⊥AB,CD为直径,
∴ AE=BE,弧AD=弧BD,弧AC=弧BC,
CE>DE,
故选B.
2.
【答案】
B
【解答】
证明:作OH⊥CD于H,
则CH=DH=12CD=52,
∵ BF⊥CD,
∴ OH?//?AM,
而OA=OB,
∴ HM=HN=12MN=76,
∴ DN=DH-NH=52-76=43,
故选B.
3.
【答案】
D
【解答】
解:如图①
作OE⊥AC垂足为E,交BD于点F,
∵ OE⊥AC??AC?//?BD,
∴ OF⊥BD,
∴ AE=12AC=6cm?????BF=12BD=8cm,
在Rt△AOE中
OE=OA2-AE2=102-62=8cm
同理可得:
OF=6cm
∴ EF=OE-OF=8-6=2cm;
如图②
同理可得:EF=OE+OF=8+6=14cm
综上所述两弦之间的距离为2cm或14cm.
故选D.
4.
【答案】
D
【解答】
连接OC;
在Rt△OCE中,由垂径定理知CE=DE=3,
由勾股定理得:
OC2=OE2+CE2=32+42=52,即OC=5,
所以⊙O的直径为10,
5.
【答案】
C
【解答】
解:拱桥的跨度AB=24m,拱高CD=8m,
∴ AD=12m,
利用勾股定理可得:122=AO2-(AO-8)2,
解得AO=13m.
即圆弧半径为13米.
故选C.
6.
【答案】
B
【解答】
解:设该铅球的半径是r.
在由铅球的半径、小坑的半径即半弦和弦心距组成的直角三角形中,
根据勾股定理,得r2=(r-2)2+25,
解得r=7.25,∴ 2r=14.5.
故选B.
7.
【答案】
B
【解答】
解:A、无法判定BM=OM,故本选项错误;
B、∵ AB为⊙O的直径,B为CD的中点,∴ AB⊥CD,故本选项正确;
C、当点M为OC的中点时,OM=12OC,故本选项错误;
D、无法判定∠BOC=60?,故本选项错误.
故选B.
8.
【答案】
A
【解答】
解:连接AO,如图:
由垂径定理,得
AE=BE.
在△AEO和△BEO中,
AE=BE∠AEO=BEOOE=OE,
∴ △AEO?△BEO(SAS),
∴ ∠AOD=∠BOD.
由圆周角定理,得
∠C=12∠AOD.
由等量代换,得
∠C=12∠BOD,故A正确.
故选:A.
9.
【答案】
B
【解答】
解:如图:
连接OA、OD,作OE⊥AC,OF⊥BD,垂足分别为E、F,
∵ AC⊥BD,
∴ 四边形OEPF为矩形,
已知OA=OC=2,OP=3,
设OE为x,则OF=EP=OP2-OE2=3-x2,
∴ AC=2AE=2OA2-OE2=24-x2,
BD=2DF=2OD2-OF2=2x2+1,
如设OF为y,同理可得:
AC=2y2+1,BD=24-y2,
∴ AC2+BD2=20,
由此可知AC与BD两线段的平方和为定值,
又∵ 任意对角线互相垂直的四边形的面积等于对角线乘积的12,
当AC=BD时,即y2+1=4-y2,
y=62,
AC=BD=10,
∴ 四边形ABCD的面积等于5.
故选:B.
10.
【答案】
B
【解答】
解:设此圆的半径为r,则OA=r,OD=9-r,
∵ AB=12米,CD⊥AB,
∴ AD=12AB=12×12=6米,、
在Rt△AOD中,
∵ OA=r,OD=9-r,AD=6米,、
∴ OA2=OD2+AD2,即r2=(9-r)2+62,
解得r=132米.
故选B.
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
11.
【答案】
2.6
【解答】
解:连接OA;
Rt△OAD中,AD=12AB=1米;
设⊙O的半径为R,则OA=OC=R,OD=5-R;
由勾股定理,得:OA2=AD2+OD2,即:
R2=(5-R)2+12,解得R=2.6(米);
故答案为:2.6.
12.
【答案】
AB,CD
【解答】
解:最长的弦:AB
最短的弦:CD
故答案为:AB、CD.
13.
【答案】
82,12
【解答】
解:如图,
∵ OA=6cm,OP=2cm,∴ 由勾股定理得,AP=42cm,
∴ AB=82cm,
∴ 过P的最短的弦长等于82cm,
故答案为82;12.
14.
【答案】
2,43
【解答】
解:如图,
∵ 弦AB所对的劣弧为圆的13,
∴ ∠AOB=13×360?=120?.
∵ OC⊥AB,OA=OB,
∴ AC=CB,∠OAC=30?,
∴ OC=12OA=2,AC=OA?sin60?=4×32=23,
∴ AB=2AC=43.
故答案为:2,43.
15.
【答案】
10cm
【解答】
解:如图,∵ AB=8cm,OC=3cm,且OC⊥AB,
∴ BC=12AB=4cm,
连接OB,则OB=OC2+BC2=5cm.
∴ 圆O的直径是10cm.
故答案为:10cm.
16.
【答案】
3
【解答】
解:∵ OD⊥AB于C,
∴ AC=12AB=4cm.
在直角三角形AOC中,根据勾股定理,得
OC=OA2-AC2=3(cm).
17.
【答案】
8
【解答】
解:因为跨度AB=24m,拱所在圆半径为13m,
延长CD到O,使得OC=OA,则O为圆心,
则AD=12AB=12(米),
则OA=13米,
在Rt△AOD中,DO=OA2-AD2=5,
进而得拱高CD=CO-DO=13-5=8米.
故答案为:8.
18.
【答案】
52
【解答】
连接OA,
∵ C是AB的中点,
∴ AC=12AB=2,OC⊥AB,
∴ OA2=OC2+AC2,即OA2=(OA-1)2+22,
解得,OA=52,
19.
【答案】
8cm
【解答】
解:连OD.
∵ EG=20-12=8,
∴ OG=8-5=3,
∴ GD=4,
∴ AD=2GD=8cm.
故答案为8cm.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
20.
【答案】
解:如图,设圆的半径为R米,
∵ CD平分弧AB,且CD⊥AB,
∴ 圆心O在CD的延长线上,
∴ CD平分AB,
∴ AD=12AB=6,
连OA,
在Rt△OAD中,AD=6,OA=R,OD=R-CD=R-4,
∵ OA2=OD2+AD2,
∴ R2=62+(R-4)2,
解得R=132,
即拱桥所在圆的半径132米.
【解答】
解:如图,设圆的半径为R米,
∵ CD平分弧AB,且CD⊥AB,
∴ 圆心O在CD的延长线上,
∴ CD平分AB,
∴ AD=12AB=6,
连OA,
在Rt△OAD中,AD=6,OA=R,OD=R-CD=R-4,
∵ OA2=OD2+AD2,
∴ R2=62+(R-4)2,
解得R=132,
即拱桥所在圆的半径132米.
21.
【答案】
解:连接OB,作OD⊥AB于D.OD就是圆心O到弦AB的距离.
在⊙O中,∵ OD⊥AB
∴ D是弦AB的中点
在Rt△OBD中,OB=5,DB=12AB=4
OD=OB2-DB2=3
圆心O到弦AB的距离为3.
(2)由(1)知:D是弦AB的中点
AB中点D在运动过程中始终保持OD=3
∴ 据圆的定义,在AB运动过程中,点D运动的轨迹是以O为圆心,3为半径的圆.
【解答】
解:连接OB,作OD⊥AB于D.OD就是圆心O到弦AB的距离.
在⊙O中,∵ OD⊥AB
∴ D是弦AB的中点
在Rt△OBD中,OB=5,DB=12AB=4
OD=OB2-DB2=3
圆心O到弦AB的距离为3.
(2)由(1)知:D是弦AB的中点
AB中点D在运动过程中始终保持OD=3
∴ 据圆的定义,在AB运动过程中,点D运动的轨迹是以O为圆心,3为半径的圆.
22.
【答案】
解:∵ E是AD的中点,
∴ OE⊥AD,
∴ ∠AEO=90?,
∵ ∠BAD=20?,
∴ ∠AOE=70?,
∵ OA=OC,
∴ ∠OAC=∠AOC,
∴ ∠AOC=12(180?-∠AOC)=12(180?-70?)=55?.
【解答】
解:∵ E是AD的中点,
∴ OE⊥AD,
∴ ∠AEO=90?,
∵ ∠BAD=20?,
∴ ∠AOE=70?,
∵ OA=OC,
∴ ∠OAC=∠AOC,
∴ ∠AOC=12(180?-∠AOC)=12(180?-70?)=55?.
23.
【答案】
解:(1)
M就是所求的圆的圆心;
(2)设圆的半径是r.在直角△ADM中,AM=r,AD=4,DM=r-2.
根据勾股定理即可得到:r2=42+(r-2)2解得:r=5.
即圆的半径为5cm.
【解答】
解:(1)
M就是所求的圆的圆心;
(2)设圆的半径是r.在直角△ADM中,AM=r,AD=4,DM=r-2.
根据勾股定理即可得到:r2=42+(r-2)2解得:r=5.
即圆的半径为5cm.
24.
【答案】
证明:过O作OE⊥CD于E,
∵ OE⊥CD,
∴ CE=DE.
∵ AC=BD,
∴ AC+CE=BD+DE.
∴ AE=BE.
∴ OA=OB.
∴ △OAB为等腰三角形.
【解答】
证明:过O作OE⊥CD于E,
∵ OE⊥CD,
∴ CE=DE.
∵ AC=BD,
∴ AC+CE=BD+DE.
∴ AE=BE.
∴ OA=OB.
∴ △OAB为等腰三角形.
25.
【答案】
证明:连接OM,ON,OA,OC,
∵ M、N分别为AB、CD的中点,
∴ OM⊥AB,ON⊥CD,
∴ AM=12AB,CN=12CD,
∵ ∠AMN=∠CNM,
∴ ∠NMO=∠MNO,即OM=ON,
在Rt△AOM与Rt△CON中,
∵ OM=ONOA=OC,
∴ Rt△AOM?Rt△CON(HL),
∴ AM=CN,
∴ AB=CD.
【解答】
证明:连接OM,ON,OA,OC,
∵ M、N分别为AB、CD的中点,
∴ OM⊥AB,ON⊥CD,
∴ AM=12AB,CN=12CD,
∵ ∠AMN=∠CNM,
∴ ∠NMO=∠MNO,即OM=ON,
在Rt△AOM与Rt△CON中,
∵ OM=ONOA=OC,
∴ Rt△AOM?Rt△CON(HL),
∴ AM=CN,
∴ AB=CD.
26.
【答案】
解:(1)作半径OC⊥AB,垂足为点D,连接OA,则CD即为弓形高,
∵ OC⊥AB,
∴ AD=12AB,
∵ AO=0.5,AB=0.6,
∴ AD=12AB=12×0.6=0.3,
∴ OD=AO2-AD2=0.4,
∴ CD=OC-OD=0.5-0.4=0.1米,即此时的水深为0.1米
(2)当水位上升到水面宽MN为0.8米时,直线OC与MN相交于点P
同理可得OP=0.3,
当MN与AB在圆心同侧时,水面上升的高度为0.1米;
当MN与AB在圆心异侧时,水面上升的高度为0.7米.
【解答】
解:(1)作半径OC⊥AB,垂足为点D,连接OA,则CD即为弓形高,
∵ OC⊥AB,
∴ AD=12AB,
∵ AO=0.5,AB=0.6,
∴ AD=12AB=12×0.6=0.3,
∴ OD=AO2-AD2=0.4,
∴ CD=OC-OD=0.5-0.4=0.1米,即此时的水深为0.1米
(2)当水位上升到水面宽MN为0.8米时,直线OC与MN相交于点P
同理可得OP=0.3,
当MN与AB在圆心同侧时,水面上升的高度为0.1米;
当MN与AB在圆心异侧时,水面上升的高度为0.7米.
