北师大版九年级数学下册 3.7 切线长定理 同步测试题(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学下册 3.7 切线长定理 同步测试题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 232.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 00:55:54 | ||
图片预览

文档简介
10490200106934001231900003.7 切线长定理 同步测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35?,∠P的度数为( )
A.35? B.45? C.60? D.70?
?
2. 如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70?,则∠BOC的度数为( )
A.130? B.120? C.110? D.100?
?
3. 如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为(? ? ? ? )
A.9 B.7 C.11 D.8
?
4. 如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为( )
A.8 B.9 C.10 D.11
?
5. 如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于D、E、F,则AF的长为( )
A.5 B.10 C.7.5 D.4
?
6. 如图所示,已知PA、PB切⊙O于A、B两点,C是AB上一动点,过C作⊙O的切线交PA于点M,交PB于点N,已知∠P=56?,则∠MON=( )
A.56? B.60? C.62? D.不可求
?
7. 如图,⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,下列结论一定正确的有( )个
①AF=BG??②CG=CH??③AB+CD=AD+BC??④BG A.1 B.2 C.3 D.4
?
8. 如图,△ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A.12cm B.7cm
C.6cm D.随直线MN的变化而变化
?
9. 如图,PA,PB,CD分别切于A,B,E,CD交PA,PB于C,D两点,若∠P=40?,则∠PAE+∠PBE的度数为(? ? ? ? )
A.50? B.62? C.66? D.70?
?
10. 如图所示,PA,PB是⊙O的切线,且∠APB=40?,下列说法不正确的是( )
A.PA=PB B.∠APO=20? C.∠OBP=70? D.∠AOP=70?
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?
11. 如图,PA、PB、DE分别切⊙O于A、B、C,如果△PDE的周长为8,那么PA=________.
?
12. 如图,⊙O与△PDE的边DE相切于点C,与PD、PE的延长线切于A、B两点,已知PA=10,则△PDE的周长为________.
?
13. 如图,已知PA,PB分别切⊙O于A、B,CD切⊙O于E,PO=13,AO=5,则△PCD周长为________.
?
14. 如图,一圆内切于四边形ABCD,且AB=8,CD=5,则AD+BC的长为________.
?
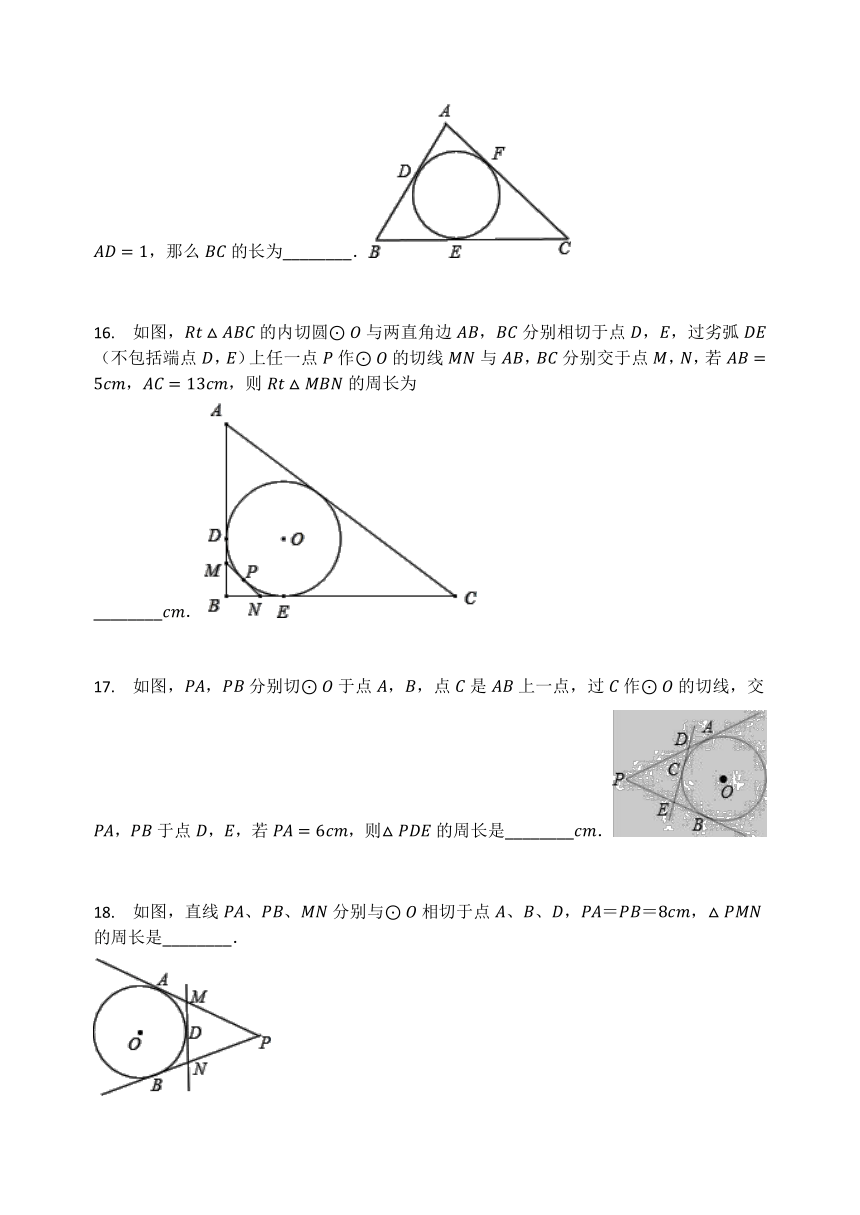
15. 如图,⊙O与△ABC的边AB、AC、BC分别相切于点D、E、F,如果AB=4,AC=5,AD=1,那么BC的长为________.
?
16. 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若AB=5cm,AC=13cm,则Rt△MBN的周长为________cm.
?
17. 如图,PA,PB分别切⊙O于点A,B,点C是AB上一点,过C作⊙O的切线,交PA,PB于点D,E,若PA=6cm,则△PDE的周长是________cm.
?
18. 如图,直线PA、PB、MN分别与⊙O相切于点A、B、D,PA=PB=8cm,△PMN的周长是________.
?
19. 如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,
已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为________.
?
20. 如图,PA、PB分别切⊙O于A、B.PA=5,在劣弧AB上取点C,过C作⊙O的切线,分别交PA,PB于D,E,则△PDE的周长等于________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 如图,圆O是三角形ABC的内切圆,求证:AB+CF=AC+BF.
?
22. 如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60?.求:
(1)PA的长;
(2)∠COD的度数.
?
23. 已知⊙O的外切等腰梯形ABCD的腰长为10,⊙O的半径为3,求等腰梯形ABCD的面积及下底的长.
?
24. 已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=10cm,求△PEF的周长.
?
25. 如图,四边形ABCD的边与圆O分别相切于点E、F、G、H,判断AB、BC、CD、DA之间有怎样的数量关系,并说明理由.
?
26. 如图,PA、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切线,切点为Q,交PA、PB于点E、F,已知PA=12cm,∠P=40?
①求△PEF的周长;
②求∠EOF的度数.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
D
【解答】
根据切线的性质定理得∠PAC=90?,
∴ ∠PAB=90?-∠BAC=90?-35?=55?.
根据切线长定理得PA=PB,
所以∠PBA=∠PAB=55?,
所以∠P=70?.
2.
【答案】
C
【解答】
∵ AB、AC是⊙O的两条切线,B、C是切点,
∴ ∠B=∠C=90?,∠BOC=180?-∠A=110?.
3.
【答案】
C
【解答】
解:如图,
设AB,AC,BC,DE和圆的切点分别是P,N,M,Q,
CM=x,根据切线长定理,得
CN=CM=x,BM=BP=9-x,AN=AP=10-x.
则有9-x+10-x=8,
解得:x=5.5.
所以△CDE的周长=CD+CE+QE+DQ
=CD+DM+CE+NE=2x=11.
故选C.
4.
【答案】
D
【解答】
解:∵ ⊙O内切于四边形ABCD,
∴ AD+BC=AB+CD,
∵ AB=10,BC=7,CD=8,
∴ AD+7=10+8,
解得:AD=11.
故选:D.
5.
【答案】
A
【解答】
解:设AF=x,根据切线长定理得AD=x,BD=BE=9-x,CE=CF=CA-AF=6-x,
则有9-x+6-x=5,解得x=5,即AF的长为5.
故选A.
6.
【答案】
C
【解答】
解:∠PMN+∠PNM=180?-∠P=124?,
∠AMN+∠BNM=360?-124?=236?,
∵ MA、MC是⊙O的切线,
∴ ∠AMO=∠CMO,
∵ NB、NC是⊙O的切线,
∴ ∠BNO=∠CNO,
∴ ∠CMO+∠CNO=12(∠AMN+∠BNM)=118?,
∴ ∠MON=180?-118?=62?,
故选:C.
7.
【答案】
B
【解答】
解:如图,连接OE、OF、OH、OG.
①∵ ⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,
∴ BF=BG、AF=AE,
只有当点F是边AB的中点时,AF=BF=BG,否则,等式AF=BG不成立;
故本选项不一定正确;
②根据题意,知,CG、CH都是⊙O的切线,
∴ CG=CH.
故本选项正确;
③根据题意,知
AF=AE,DH=DE,BF=BG,CG=CH,
则AF+BF+CH+DH=AE+BG+CG+DE,即AB+CD=AD+BC.
故本选项正确;
④当点G是边BC的中点时,BG=CG.
故本选项错误;
综上所述,正确的说法有2个;
故选B.
8.
【答案】
B
【解答】
设E、F分别是⊙O的切点,
∵ △ABC是一张三角形的纸片,AB+BC+AC=17cm,⊙O是它的内切圆,点D是其中的一个切点,BC=5cm,
∴ BD+CE=BC=5cm,则AD+AE=7cm,
故DM=MF,FN=EN,AD=AE,
∴ AM+AN+MN=AD+AE=7(cm).
9.
【答案】
D
【解答】
解:∵ PA,PB,CD分别切⊙O于A,B,E,CD交PA,PB于C,D两点,
∴ CE=CA,DE=DB,
∴ ∠CAE=∠CEA,∠DEB=∠DBE,
∴ ∠PCD=∠CAE+∠CEA=2∠CAE,
∠PDC=∠DEB+∠DBE=2∠DBE,
∴ ∠CAE=12∠PCD,∠DBE=12∠PDC,
即∠PAE=12∠PCD,∠PBE=12∠PDC,
∵ ∠P=40?,
∴ ∠PAE+∠PBE=12∠PCD+12∠PDC
=12(∠PCD+∠PDC)=12(180?-∠P)=70?.
故选D.
10.
【答案】
C
【解答】
解:∵ PA,PB是⊙O的切线,且∠APB=40?,
∴ PA=PB,∠APO=∠BPO,∠A=∠B=90?,
∴ ∠OBP=∠OAP,
∴ C是错误的.
故选C.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
4
【解答】
解:∵ PA、PB、DE分别切⊙O于A、B、C,
∴ PA=PB,DA=DC,EC=EB;
∴ C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=8;
∴ PA=PB=4,
故答案为4.
12.
【答案】
20
【解答】
解:∵ PA、PB、DE分别切⊙O于A、B、C,
∴ PA=PB,DA=DC,EC=EB;
∴ C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=10+10=20.
∴ △PDE的周长为20.
故答案为20.
13.
【答案】
24
【解答】
解:连接OB.
∵ PA是⊙O的切线,点A是切点,
∴ PA⊥OA;
∴ PA=PO2-OA2=12;
∵ PA、PB为圆的两条相交切线,
∴ PA=PB;
同理可得:CA=CE,DE=DB.
∵ △PCD的周长=PC+CE+ED+PD,
∴ △PCD的周长=PC+CA+BD+PD=PA+PB=2PA,
∴ △PCD的周长=24;
故答案是:24.
14.
【答案】
13
【解答】
解:由题意可得圆外切四边形的两组对边和相等,所以AD+BC=AB+CD=5+8=13,故选答案是:13.
15.
【答案】
7
【解答】
解:∵ AB、AC、BC都是⊙O的切线,
∴ AD=AE,BD=BF,CE=CF,
∵ AB=4,AC=5,AD=1,
∴ AE=1,BD=3,CE=CF=4,
∴ BC=BF+CF=3+4=7.
16.
【答案】
4
【解答】
解:如图所示:连接DO,EO,
Rt△ABC中,AB=5cm,AC=13cm,则BC=12cm,
设△ABC内切圆的半径为R,切点分别为D、E、F,
∵ AD=AF,BE=BD,CF=CE,
∵ OD⊥AB,OE⊥BC,
∴ 四边形ODBE是正方形,即BD=BE=R,
∴ AB-BD=AF,CB-BE=FC,
5-R+12-R=13,
解得:R=2,
∵ 切线MN与AB,BC分别交于点M,N,
∴ MP=DM,PN=NE,
∴ Rt△MBN的周长为:BD+BE=2+2=4(cm),
故答案为:4.
17.
【答案】
12
【解答】
解:根据切线长定理得:AD=CD,BE=CE,PA=PB,则△PDE的周长=2PA=12cm.
18.
【答案】
16cm
【解答】
∵ 直线PA、PB、MN分别与⊙O相切于点A、B、D,
∴ MA=MD,ND=NB,
∴ △PMN的周长=PM+PN+MD+ND=PM+MA+PN+NB=PA+PB=8+8=16(cm).
19.
【答案】
20cm
【解答】
解:∵ △ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,AD=10cm,
∴ 设E、F分别是⊙O的切点,
故DM=MF,FN=EN,AD=AE,
∴ AM+AN+MN=AD+AE=10+10=20(cm).
故答案是:20cm.
20.
【答案】
10
【解答】
解:∵ PA、PB、DE分别切⊙O于A、B、C,
∴ PA=PB,DA=DC,EC=EB;
∴ C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=10;
故△PDE的周长为10.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
证明:∵ 圆O是三角形ABC的内切圆,
∴ AD=AE①,BD=BF②,CF=CE③,
∴ ①+②+③得,AD+BD+CF=AE+BF+CE,
∴ AB+CF=AC+BF.
【解答】
证明:∵ 圆O是三角形ABC的内切圆,
∴ AD=AE①,BD=BF②,CF=CE③,
∴ ①+②+③得,AD+BD+CF=AE+BF+CE,
∴ AB+CF=AC+BF.
22.
【答案】
∵ CA,CE都是圆O的切线,
∴ CA=CE,
同理DE=DB,PA=PB,
∴ 三角形PDE的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
∵ ∠P=60?,
∴ ∠PCE+∠PDE=120?,
∴ ∠ACD+∠CDB=360?-120?=240?,
∵ CA,CE是圆O的切线,
∴ ∠OCE=∠OCA=12∠ACD;
同理:∠ODE=12∠CDB,
∴ ∠OCE+∠ODE=12(∠ACD+∠CDB)=120?,
∴ ∠COD=180-120?=60?.
【解答】
∵ CA,CE都是圆O的切线,
∴ CA=CE,
同理DE=DB,PA=PB,
∴ 三角形PDE的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
∵ ∠P=60?,
∴ ∠PCE+∠PDE=120?,
∴ ∠ACD+∠CDB=360?-120?=240?,
∵ CA,CE是圆O的切线,
∴ ∠OCE=∠OCA=12∠ACD;
同理:∠ODE=12∠CDB,
∴ ∠OCE+∠ODE=12(∠ACD+∠CDB)=120?,
∴ ∠COD=180-120?=60?.
23.
【答案】
解:作AB⊥CD于E,BF⊥CD与F,如图,
∵ ⊙O为等腰梯形ABCD的内切圆,
∴ AB+CD=AD+BC=20,
∵ AB?//?CD,
∴ AE=6,
∴ 等腰梯形ABCD的面积=12(AB+CD)?AE=12×20×6=60;
在Rt△ADE中,∵ AD=10,AE=6,
∴ DE=AD2-AE2=8,
∵ 梯形ABCD为等腰梯形,
∴ CF=DE=8,
而AB+CD=20,AB=EF,
∴ 8+8+2EF=20,解得EF=2,
∴ 梯形的下底CD=8+2+8=18.
【解答】
解:作AB⊥CD于E,BF⊥CD与F,如图,
∵ ⊙O为等腰梯形ABCD的内切圆,
∴ AB+CD=AD+BC=20,
∵ AB?//?CD,
∴ AE=6,
∴ 等腰梯形ABCD的面积=12(AB+CD)?AE=12×20×6=60;
在Rt△ADE中,∵ AD=10,AE=6,
∴ DE=AD2-AE2=8,
∵ 梯形ABCD为等腰梯形,
∴ CF=DE=8,
而AB+CD=20,AB=EF,
∴ 8+8+2EF=20,解得EF=2,
∴ 梯形的下底CD=8+2+8=18.
24.
【答案】
△PEF的周长是20cm.
【解答】
解:∵ PA、PB是⊙O的切线,切点分别是A、B,
∴ PA=PB=10cm,
∵ 过Q点作⊙O的切线,交PA、PB于E、F点,
∴ EB=EQ,FQ=FA,
∴ △PEF的周长是:PE+EF+PF=PE+EQ+FQ+PF,
=PE+EB+PF+FA=PB+PA=10+10=20(cm),
25.
【答案】
解:AD+BC=CD+AB,
理由:∵ 四边形ABCD的边与圆O分别相切于点E、F、G、H,
∴ DH=DG,CG=CF,BE=BF,AE=AH,
∴ AH+DH+CF+BF=DG+GC+AE+BE,
即AD+BC=CD+AB.
【解答】
解:AD+BC=CD+AB,
理由:∵ 四边形ABCD的边与圆O分别相切于点E、F、G、H,
∴ DH=DG,CG=CF,BE=BF,AE=AH,
∴ AH+DH+CF+BF=DG+GC+AE+BE,
即AD+BC=CD+AB.
26.
【答案】
解:①∵ PA、PB是⊙O的切线,
∴ PA=PB,
又∵ 直线EF是⊙O的切线,
∴ EB=EQ,FQ=FA,
∴ △PEF的周长=PE+PF+EF=PE+PF+EB+FA=PA+PB=2PA=24cm;
②连接OE,OF,则OE平分∠BEF,OF平分∠AFE,
则∠OEF+∠OFE=12(∠P+∠PFE)+12∠(P+∠PEF)=12(180?+40?)=110?,
∴ ∠EOF=180?-110?=70?.
【解答】
解:①∵ PA、PB是⊙O的切线,
∴ PA=PB,
又∵ 直线EF是⊙O的切线,
∴ EB=EQ,FQ=FA,
∴ △PEF的周长=PE+PF+EF=PE+PF+EB+FA=PA+PB=2PA=24cm;
②连接OE,OF,则OE平分∠BEF,OF平分∠AFE,
则∠OEF+∠OFE=12(∠P+∠PFE)+12∠(P+∠PEF)=12(180?+40?)=110?,
∴ ∠EOF=180?-110?=70?.∴ sin∠DHE=DMDH=32212=217.
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35?,∠P的度数为( )
A.35? B.45? C.60? D.70?
?
2. 如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70?,则∠BOC的度数为( )
A.130? B.120? C.110? D.100?
?
3. 如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为(? ? ? ? )
A.9 B.7 C.11 D.8
?
4. 如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为( )
A.8 B.9 C.10 D.11
?
5. 如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于D、E、F,则AF的长为( )
A.5 B.10 C.7.5 D.4
?
6. 如图所示,已知PA、PB切⊙O于A、B两点,C是AB上一动点,过C作⊙O的切线交PA于点M,交PB于点N,已知∠P=56?,则∠MON=( )
A.56? B.60? C.62? D.不可求
?
7. 如图,⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,下列结论一定正确的有( )个
①AF=BG??②CG=CH??③AB+CD=AD+BC??④BG
?
8. 如图,△ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A.12cm B.7cm
C.6cm D.随直线MN的变化而变化
?
9. 如图,PA,PB,CD分别切于A,B,E,CD交PA,PB于C,D两点,若∠P=40?,则∠PAE+∠PBE的度数为(? ? ? ? )
A.50? B.62? C.66? D.70?
?
10. 如图所示,PA,PB是⊙O的切线,且∠APB=40?,下列说法不正确的是( )
A.PA=PB B.∠APO=20? C.∠OBP=70? D.∠AOP=70?
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?
11. 如图,PA、PB、DE分别切⊙O于A、B、C,如果△PDE的周长为8,那么PA=________.
?
12. 如图,⊙O与△PDE的边DE相切于点C,与PD、PE的延长线切于A、B两点,已知PA=10,则△PDE的周长为________.
?
13. 如图,已知PA,PB分别切⊙O于A、B,CD切⊙O于E,PO=13,AO=5,则△PCD周长为________.
?
14. 如图,一圆内切于四边形ABCD,且AB=8,CD=5,则AD+BC的长为________.
?
15. 如图,⊙O与△ABC的边AB、AC、BC分别相切于点D、E、F,如果AB=4,AC=5,AD=1,那么BC的长为________.
?
16. 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若AB=5cm,AC=13cm,则Rt△MBN的周长为________cm.
?
17. 如图,PA,PB分别切⊙O于点A,B,点C是AB上一点,过C作⊙O的切线,交PA,PB于点D,E,若PA=6cm,则△PDE的周长是________cm.
?
18. 如图,直线PA、PB、MN分别与⊙O相切于点A、B、D,PA=PB=8cm,△PMN的周长是________.
?
19. 如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,
已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为________.
?
20. 如图,PA、PB分别切⊙O于A、B.PA=5,在劣弧AB上取点C,过C作⊙O的切线,分别交PA,PB于D,E,则△PDE的周长等于________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 如图,圆O是三角形ABC的内切圆,求证:AB+CF=AC+BF.
?
22. 如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60?.求:
(1)PA的长;
(2)∠COD的度数.
?
23. 已知⊙O的外切等腰梯形ABCD的腰长为10,⊙O的半径为3,求等腰梯形ABCD的面积及下底的长.
?
24. 已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=10cm,求△PEF的周长.
?
25. 如图,四边形ABCD的边与圆O分别相切于点E、F、G、H,判断AB、BC、CD、DA之间有怎样的数量关系,并说明理由.
?
26. 如图,PA、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切线,切点为Q,交PA、PB于点E、F,已知PA=12cm,∠P=40?
①求△PEF的周长;
②求∠EOF的度数.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
D
【解答】
根据切线的性质定理得∠PAC=90?,
∴ ∠PAB=90?-∠BAC=90?-35?=55?.
根据切线长定理得PA=PB,
所以∠PBA=∠PAB=55?,
所以∠P=70?.
2.
【答案】
C
【解答】
∵ AB、AC是⊙O的两条切线,B、C是切点,
∴ ∠B=∠C=90?,∠BOC=180?-∠A=110?.
3.
【答案】
C
【解答】
解:如图,
设AB,AC,BC,DE和圆的切点分别是P,N,M,Q,
CM=x,根据切线长定理,得
CN=CM=x,BM=BP=9-x,AN=AP=10-x.
则有9-x+10-x=8,
解得:x=5.5.
所以△CDE的周长=CD+CE+QE+DQ
=CD+DM+CE+NE=2x=11.
故选C.
4.
【答案】
D
【解答】
解:∵ ⊙O内切于四边形ABCD,
∴ AD+BC=AB+CD,
∵ AB=10,BC=7,CD=8,
∴ AD+7=10+8,
解得:AD=11.
故选:D.
5.
【答案】
A
【解答】
解:设AF=x,根据切线长定理得AD=x,BD=BE=9-x,CE=CF=CA-AF=6-x,
则有9-x+6-x=5,解得x=5,即AF的长为5.
故选A.
6.
【答案】
C
【解答】
解:∠PMN+∠PNM=180?-∠P=124?,
∠AMN+∠BNM=360?-124?=236?,
∵ MA、MC是⊙O的切线,
∴ ∠AMO=∠CMO,
∵ NB、NC是⊙O的切线,
∴ ∠BNO=∠CNO,
∴ ∠CMO+∠CNO=12(∠AMN+∠BNM)=118?,
∴ ∠MON=180?-118?=62?,
故选:C.
7.
【答案】
B
【解答】
解:如图,连接OE、OF、OH、OG.
①∵ ⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,
∴ BF=BG、AF=AE,
只有当点F是边AB的中点时,AF=BF=BG,否则,等式AF=BG不成立;
故本选项不一定正确;
②根据题意,知,CG、CH都是⊙O的切线,
∴ CG=CH.
故本选项正确;
③根据题意,知
AF=AE,DH=DE,BF=BG,CG=CH,
则AF+BF+CH+DH=AE+BG+CG+DE,即AB+CD=AD+BC.
故本选项正确;
④当点G是边BC的中点时,BG=CG.
故本选项错误;
综上所述,正确的说法有2个;
故选B.
8.
【答案】
B
【解答】
设E、F分别是⊙O的切点,
∵ △ABC是一张三角形的纸片,AB+BC+AC=17cm,⊙O是它的内切圆,点D是其中的一个切点,BC=5cm,
∴ BD+CE=BC=5cm,则AD+AE=7cm,
故DM=MF,FN=EN,AD=AE,
∴ AM+AN+MN=AD+AE=7(cm).
9.
【答案】
D
【解答】
解:∵ PA,PB,CD分别切⊙O于A,B,E,CD交PA,PB于C,D两点,
∴ CE=CA,DE=DB,
∴ ∠CAE=∠CEA,∠DEB=∠DBE,
∴ ∠PCD=∠CAE+∠CEA=2∠CAE,
∠PDC=∠DEB+∠DBE=2∠DBE,
∴ ∠CAE=12∠PCD,∠DBE=12∠PDC,
即∠PAE=12∠PCD,∠PBE=12∠PDC,
∵ ∠P=40?,
∴ ∠PAE+∠PBE=12∠PCD+12∠PDC
=12(∠PCD+∠PDC)=12(180?-∠P)=70?.
故选D.
10.
【答案】
C
【解答】
解:∵ PA,PB是⊙O的切线,且∠APB=40?,
∴ PA=PB,∠APO=∠BPO,∠A=∠B=90?,
∴ ∠OBP=∠OAP,
∴ C是错误的.
故选C.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
4
【解答】
解:∵ PA、PB、DE分别切⊙O于A、B、C,
∴ PA=PB,DA=DC,EC=EB;
∴ C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=8;
∴ PA=PB=4,
故答案为4.
12.
【答案】
20
【解答】
解:∵ PA、PB、DE分别切⊙O于A、B、C,
∴ PA=PB,DA=DC,EC=EB;
∴ C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=10+10=20.
∴ △PDE的周长为20.
故答案为20.
13.
【答案】
24
【解答】
解:连接OB.
∵ PA是⊙O的切线,点A是切点,
∴ PA⊥OA;
∴ PA=PO2-OA2=12;
∵ PA、PB为圆的两条相交切线,
∴ PA=PB;
同理可得:CA=CE,DE=DB.
∵ △PCD的周长=PC+CE+ED+PD,
∴ △PCD的周长=PC+CA+BD+PD=PA+PB=2PA,
∴ △PCD的周长=24;
故答案是:24.
14.
【答案】
13
【解答】
解:由题意可得圆外切四边形的两组对边和相等,所以AD+BC=AB+CD=5+8=13,故选答案是:13.
15.
【答案】
7
【解答】
解:∵ AB、AC、BC都是⊙O的切线,
∴ AD=AE,BD=BF,CE=CF,
∵ AB=4,AC=5,AD=1,
∴ AE=1,BD=3,CE=CF=4,
∴ BC=BF+CF=3+4=7.
16.
【答案】
4
【解答】
解:如图所示:连接DO,EO,
Rt△ABC中,AB=5cm,AC=13cm,则BC=12cm,
设△ABC内切圆的半径为R,切点分别为D、E、F,
∵ AD=AF,BE=BD,CF=CE,
∵ OD⊥AB,OE⊥BC,
∴ 四边形ODBE是正方形,即BD=BE=R,
∴ AB-BD=AF,CB-BE=FC,
5-R+12-R=13,
解得:R=2,
∵ 切线MN与AB,BC分别交于点M,N,
∴ MP=DM,PN=NE,
∴ Rt△MBN的周长为:BD+BE=2+2=4(cm),
故答案为:4.
17.
【答案】
12
【解答】
解:根据切线长定理得:AD=CD,BE=CE,PA=PB,则△PDE的周长=2PA=12cm.
18.
【答案】
16cm
【解答】
∵ 直线PA、PB、MN分别与⊙O相切于点A、B、D,
∴ MA=MD,ND=NB,
∴ △PMN的周长=PM+PN+MD+ND=PM+MA+PN+NB=PA+PB=8+8=16(cm).
19.
【答案】
20cm
【解答】
解:∵ △ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,AD=10cm,
∴ 设E、F分别是⊙O的切点,
故DM=MF,FN=EN,AD=AE,
∴ AM+AN+MN=AD+AE=10+10=20(cm).
故答案是:20cm.
20.
【答案】
10
【解答】
解:∵ PA、PB、DE分别切⊙O于A、B、C,
∴ PA=PB,DA=DC,EC=EB;
∴ C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=10;
故△PDE的周长为10.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
证明:∵ 圆O是三角形ABC的内切圆,
∴ AD=AE①,BD=BF②,CF=CE③,
∴ ①+②+③得,AD+BD+CF=AE+BF+CE,
∴ AB+CF=AC+BF.
【解答】
证明:∵ 圆O是三角形ABC的内切圆,
∴ AD=AE①,BD=BF②,CF=CE③,
∴ ①+②+③得,AD+BD+CF=AE+BF+CE,
∴ AB+CF=AC+BF.
22.
【答案】
∵ CA,CE都是圆O的切线,
∴ CA=CE,
同理DE=DB,PA=PB,
∴ 三角形PDE的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
∵ ∠P=60?,
∴ ∠PCE+∠PDE=120?,
∴ ∠ACD+∠CDB=360?-120?=240?,
∵ CA,CE是圆O的切线,
∴ ∠OCE=∠OCA=12∠ACD;
同理:∠ODE=12∠CDB,
∴ ∠OCE+∠ODE=12(∠ACD+∠CDB)=120?,
∴ ∠COD=180-120?=60?.
【解答】
∵ CA,CE都是圆O的切线,
∴ CA=CE,
同理DE=DB,PA=PB,
∴ 三角形PDE的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
∵ ∠P=60?,
∴ ∠PCE+∠PDE=120?,
∴ ∠ACD+∠CDB=360?-120?=240?,
∵ CA,CE是圆O的切线,
∴ ∠OCE=∠OCA=12∠ACD;
同理:∠ODE=12∠CDB,
∴ ∠OCE+∠ODE=12(∠ACD+∠CDB)=120?,
∴ ∠COD=180-120?=60?.
23.
【答案】
解:作AB⊥CD于E,BF⊥CD与F,如图,
∵ ⊙O为等腰梯形ABCD的内切圆,
∴ AB+CD=AD+BC=20,
∵ AB?//?CD,
∴ AE=6,
∴ 等腰梯形ABCD的面积=12(AB+CD)?AE=12×20×6=60;
在Rt△ADE中,∵ AD=10,AE=6,
∴ DE=AD2-AE2=8,
∵ 梯形ABCD为等腰梯形,
∴ CF=DE=8,
而AB+CD=20,AB=EF,
∴ 8+8+2EF=20,解得EF=2,
∴ 梯形的下底CD=8+2+8=18.
【解答】
解:作AB⊥CD于E,BF⊥CD与F,如图,
∵ ⊙O为等腰梯形ABCD的内切圆,
∴ AB+CD=AD+BC=20,
∵ AB?//?CD,
∴ AE=6,
∴ 等腰梯形ABCD的面积=12(AB+CD)?AE=12×20×6=60;
在Rt△ADE中,∵ AD=10,AE=6,
∴ DE=AD2-AE2=8,
∵ 梯形ABCD为等腰梯形,
∴ CF=DE=8,
而AB+CD=20,AB=EF,
∴ 8+8+2EF=20,解得EF=2,
∴ 梯形的下底CD=8+2+8=18.
24.
【答案】
△PEF的周长是20cm.
【解答】
解:∵ PA、PB是⊙O的切线,切点分别是A、B,
∴ PA=PB=10cm,
∵ 过Q点作⊙O的切线,交PA、PB于E、F点,
∴ EB=EQ,FQ=FA,
∴ △PEF的周长是:PE+EF+PF=PE+EQ+FQ+PF,
=PE+EB+PF+FA=PB+PA=10+10=20(cm),
25.
【答案】
解:AD+BC=CD+AB,
理由:∵ 四边形ABCD的边与圆O分别相切于点E、F、G、H,
∴ DH=DG,CG=CF,BE=BF,AE=AH,
∴ AH+DH+CF+BF=DG+GC+AE+BE,
即AD+BC=CD+AB.
【解答】
解:AD+BC=CD+AB,
理由:∵ 四边形ABCD的边与圆O分别相切于点E、F、G、H,
∴ DH=DG,CG=CF,BE=BF,AE=AH,
∴ AH+DH+CF+BF=DG+GC+AE+BE,
即AD+BC=CD+AB.
26.
【答案】
解:①∵ PA、PB是⊙O的切线,
∴ PA=PB,
又∵ 直线EF是⊙O的切线,
∴ EB=EQ,FQ=FA,
∴ △PEF的周长=PE+PF+EF=PE+PF+EB+FA=PA+PB=2PA=24cm;
②连接OE,OF,则OE平分∠BEF,OF平分∠AFE,
则∠OEF+∠OFE=12(∠P+∠PFE)+12∠(P+∠PEF)=12(180?+40?)=110?,
∴ ∠EOF=180?-110?=70?.
【解答】
解:①∵ PA、PB是⊙O的切线,
∴ PA=PB,
又∵ 直线EF是⊙O的切线,
∴ EB=EQ,FQ=FA,
∴ △PEF的周长=PE+PF+EF=PE+PF+EB+FA=PA+PB=2PA=24cm;
②连接OE,OF,则OE平分∠BEF,OF平分∠AFE,
则∠OEF+∠OFE=12(∠P+∠PFE)+12∠(P+∠PEF)=12(180?+40?)=110?,
∴ ∠EOF=180?-110?=70?.∴ sin∠DHE=DMDH=32212=217.
