六年级数学下册教案式与方程人教版
图片预览


文档简介
《式与方程的整理和复习》教学设计
教学内容:义务教育教科书《小学数学》六年级下册。
教学目标:
1.经历回顾和整理式与方程有关知识的过程。
2.会用方程表示简单的等量关系,会列方程解决简单问题。
3.感受式与方程在解决问题中的价值,培养初步的代数思想。
教学重、难点:
经历回顾和整理式与方程有关知识的过程,感受式与方程在解决问题中的价值,培养初步的代数思想。
教具准备:教学课件
教学过程:
激情导入:
师:同学们,上几节课我们已经整理了数与代数的一部分知识,这节课我们就一起回顾、整理数与代数中的 “式与方程的整理和复习”。(直接揭示课题)
(齐读课题):式与方程
一、明确整理目标,梳理知识网络
师:《式与方程》这部分内容我们都学过哪些知识呢?请同学们快速回忆一下,并你的同桌说一说这些知识。
学生回答,老师整理知识框架。
用字母表示数
认识方程
解方程
运用方程解决实际问题
师:同学们真棒,掌声送给自己!把这些知识点放在一起就是我们本节课要整理的内容(板书)。
二、整理用字母表示数
(一)师:在我们六年的数学学习中,学过很多用字母表示数的知识,下面就请同学们回忆一下,哪些数或者数量关系可以用字母来表示?
生: 1、用字母表示数字
2、用字母表示数量关系
3、用字母表示计算公式
4、用字母表示运算定律
5、还可以用字母表示其它
(二)根据学生的举例回答,并通过多媒体课件,罗列出各种字母表示数的类型。
师:非常棒!
(三)整理用字母表示数各种情况
1、请同学们举例用字母表示具体数量的例子
如:一个班有男生a人,有女生b人,那么a+b表示( ),a-b表示( )。
每包有m颗糖,n包有( )颗糖。
甲衣服x元,乙衣服y元,甲的价钱是乙的( )。
师:谁还能举其它的例子?
2、用字母表示数量关系。
师:如果用s表示路程,v表示速度,t表示时间,他们三者之间有什么关系呢?
生:S=v t;v=s÷t t=s÷v
师:谁能用字母来表示单价、数量和总价的关系?
生回答。
3、用字母计算公式
师课件出示各种已学的平面图形,请同学们用字母表示出它们的周长计算公式和面积计算公式:
C=2(a+b) c=4a s=ah
S=ab s=a.a
c=πd=2πr
S=ah÷2 s=(a+b)h÷2 S=πr2
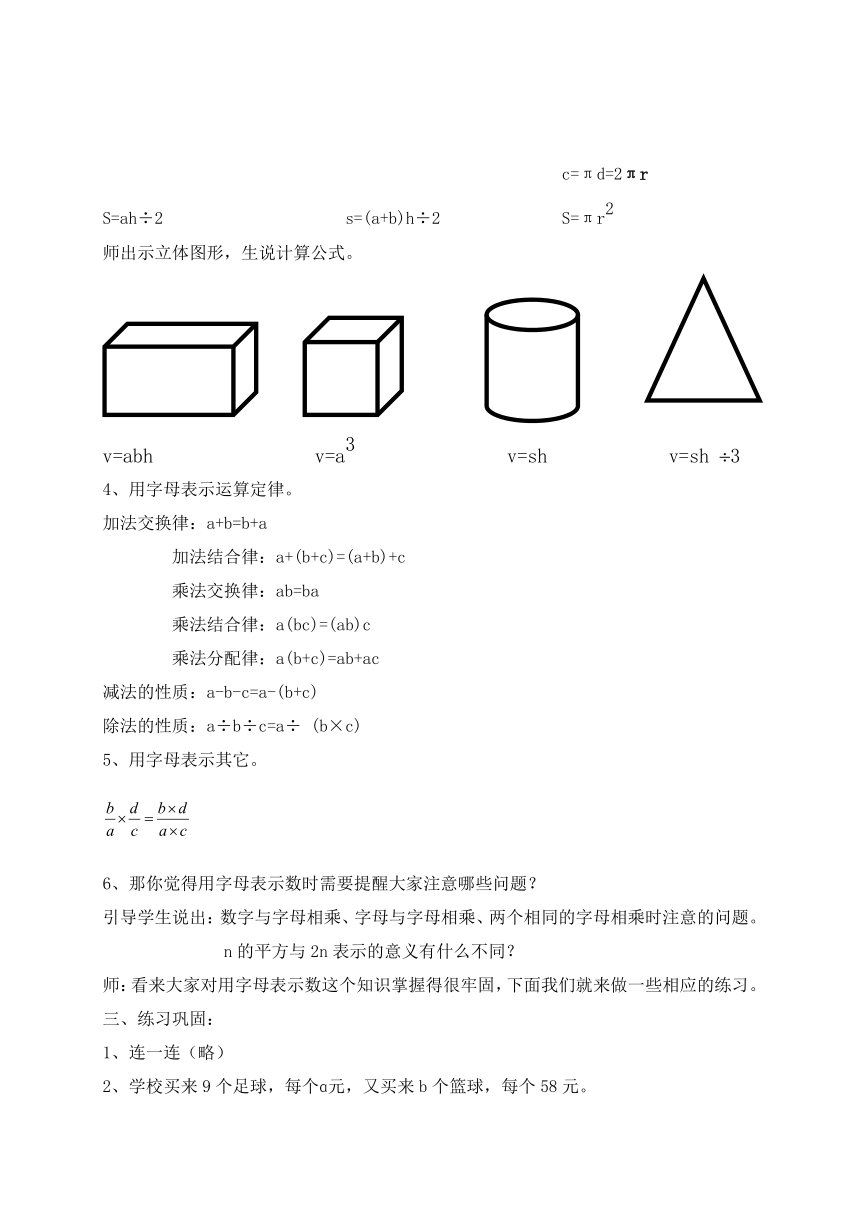
师出示立体图形,生说计算公式。
v=abh v=a3 v=sh v=sh 3
4、用字母表示运算定律。
加法交换律:a+b=b+a
加法结合律:a+(b+c)=(a+b)+c
乘法交换律:ab=ba
乘法结合律:a(bc)=(ab)c
乘法分配律:a(b+c)=ab+ac
减法的性质:a-b-c=a-(b+c)
除法的性质:a÷b÷c=a÷ (b×c)
5、用字母表示其它。
false6、那你觉得用字母表示数时需要提醒大家注意哪些问题?
引导学生说出:数字与字母相乘、字母与字母相乘、两个相同的字母相乘时注意的问题。
n的平方与2n表示的意义有什么不同?
师:看来大家对用字母表示数这个知识掌握得很牢固,下面我们就来做一些相应的练习。
三、练习巩固:
1、连一连(略)
2、学校买来9个足球,每个ɑ元,又买来b个篮球,每个58元。
9 ɑ表示
58 b表示
58- ɑ表示
9 ɑ+ 58 b表示
如果ɑ = 45, b = 6,则9 ɑ+ 58 b=
3、填空练习。
(1)小红今年m 岁,陈老师的岁数比她的3倍少8岁。陈老师的岁数( )岁。如果m=12,陈老师今年是( )岁。
(2)修一条长a千米的路,如果每天修2千米。修了b天后,还剩( )千米。
(3)三个连续的自然数,最大的一个是a,那么最小的一个数是( )。
(4)长方形的宽是m米,长是宽的2倍,长方形的周长是( )米,面积是( )平方米。
(5)一种贺卡的单价是a元,小英买5张这样的贺卡。用去( )元;小明买n张这样的贺卡,付出10元,应找回( )元。
(6)每千瓦时电费0.52元,每立方米水费2元。小明家本月用了a千瓦时电和b立方米水,一共要付水电费( )元。
4、选择。
(1)小涛看一本书,第一天看了全书的20%全书有x页。还剩( )页。
A、20% x B、x -20% C、x - 20%x
(2)小刚今年a 岁,小红今年(a+5)岁,再过x年后,他们相差( )岁。
A、5 B、x C、x +5
(3)在 5+2x>10、 x+x-18、 x = 3 、11+13=4×6、 X- 0.5x = 2 等5个式子中,有( )个方程。
A、3 B、2 C、4
(4)m是奇数,n是偶数,下面结果是奇数的式子是( )。
A、3m +n B、2m+n C、2(m+n)
四、整理方程的知识
(一)师:什么是等式?什么是方程?什么叫解方程?什么叫方程的解?(老师一口气抛出几个问题,学生带着问题思考)
师随学生回答大屏幕出示方程的定义:
生齐读
出示一组式子,生判断是不是方程并说明理由。
?100-35=65??
x-13>72
x+36
4+0.7x=102
32=16×2
结合前两个算式学生用自己喜欢的表达方式来说说方程与等式的关系
我们可以用一句话概括:
生:方程一定是等式,但等式不一定是方程。(图示)
等式
方程
师:请同学们判断
1)0.5x>1是方程。( )
2)含有未知数的式子是方程。( )
3)方程是等式,等式也是方程。( )
(二)解方程。请同学们计算下面两道。
x-3.5+8=16 8x-4.8x=1.6
师总结:希望同学们能够养成做完题后自觉检查的好习惯。
下面我们就用解方程的知识来解决两道生活中的实际问题。
做完和同桌交流做法,说出根据什么等量关系解方程。
学生展示不同的做法,师小结:
等式的基本性质
1 、等式的左边和右边同时加上(或减去)同一个数,左右两边仍然相等。
2 、等式的左边和右边同时乘以(或除以)一个非0的数,左右两边仍然相等。
五、解决实际问题;
1、学生回忆用方程解决实际问题的步骤
读题,弄清题意,设未知数。
分析题意,找出数量关系式。
列方程,并解方程。
检验,写出答案。
2、完成相应的练习
(1)学校组织远足活动。原计划每小时走3.8km,3小时到达目的地。实际2.5小时走完了原定路程,平均每小时走了多少千米?
(2)一种树苗实验成活率是95%,为了保证成活380棵,至少要种多少棵树苗?
(3)小平在踢毽比赛中踢了42下,她踢毽的数量是小云的false。小云踢了多少下?
师:这节课我们一起回顾、整理了很多式与方程的知识,收获知识不是最快乐的,用我们收获的知识去解决无数的数学问题才是我们学习数学的最大乐趣。你们说对不对。那你们愿意把你们收获的知识和老师一起分享吗?
学生谈收获!
六、作业布置:(略)
七、板书设计: 式与方程的整理和复习
1、用字母表示数字
用字母表示数
2、用字母表示数量关系
式与方程
3、用字母表示计算公式
4、用字母表示运算定律
5、还可以用字母表示其它
简易方程
1、解方程
2、用方程解决实际问题
教学内容:义务教育教科书《小学数学》六年级下册。
教学目标:
1.经历回顾和整理式与方程有关知识的过程。
2.会用方程表示简单的等量关系,会列方程解决简单问题。
3.感受式与方程在解决问题中的价值,培养初步的代数思想。
教学重、难点:
经历回顾和整理式与方程有关知识的过程,感受式与方程在解决问题中的价值,培养初步的代数思想。
教具准备:教学课件
教学过程:
激情导入:
师:同学们,上几节课我们已经整理了数与代数的一部分知识,这节课我们就一起回顾、整理数与代数中的 “式与方程的整理和复习”。(直接揭示课题)
(齐读课题):式与方程
一、明确整理目标,梳理知识网络
师:《式与方程》这部分内容我们都学过哪些知识呢?请同学们快速回忆一下,并你的同桌说一说这些知识。
学生回答,老师整理知识框架。
用字母表示数
认识方程
解方程
运用方程解决实际问题
师:同学们真棒,掌声送给自己!把这些知识点放在一起就是我们本节课要整理的内容(板书)。
二、整理用字母表示数
(一)师:在我们六年的数学学习中,学过很多用字母表示数的知识,下面就请同学们回忆一下,哪些数或者数量关系可以用字母来表示?
生: 1、用字母表示数字
2、用字母表示数量关系
3、用字母表示计算公式
4、用字母表示运算定律
5、还可以用字母表示其它
(二)根据学生的举例回答,并通过多媒体课件,罗列出各种字母表示数的类型。
师:非常棒!
(三)整理用字母表示数各种情况
1、请同学们举例用字母表示具体数量的例子
如:一个班有男生a人,有女生b人,那么a+b表示( ),a-b表示( )。
每包有m颗糖,n包有( )颗糖。
甲衣服x元,乙衣服y元,甲的价钱是乙的( )。
师:谁还能举其它的例子?
2、用字母表示数量关系。
师:如果用s表示路程,v表示速度,t表示时间,他们三者之间有什么关系呢?
生:S=v t;v=s÷t t=s÷v
师:谁能用字母来表示单价、数量和总价的关系?
生回答。
3、用字母计算公式
师课件出示各种已学的平面图形,请同学们用字母表示出它们的周长计算公式和面积计算公式:
C=2(a+b) c=4a s=ah
S=ab s=a.a
c=πd=2πr
S=ah÷2 s=(a+b)h÷2 S=πr2
师出示立体图形,生说计算公式。
v=abh v=a3 v=sh v=sh 3
4、用字母表示运算定律。
加法交换律:a+b=b+a
加法结合律:a+(b+c)=(a+b)+c
乘法交换律:ab=ba
乘法结合律:a(bc)=(ab)c
乘法分配律:a(b+c)=ab+ac
减法的性质:a-b-c=a-(b+c)
除法的性质:a÷b÷c=a÷ (b×c)
5、用字母表示其它。
false6、那你觉得用字母表示数时需要提醒大家注意哪些问题?
引导学生说出:数字与字母相乘、字母与字母相乘、两个相同的字母相乘时注意的问题。
n的平方与2n表示的意义有什么不同?
师:看来大家对用字母表示数这个知识掌握得很牢固,下面我们就来做一些相应的练习。
三、练习巩固:
1、连一连(略)
2、学校买来9个足球,每个ɑ元,又买来b个篮球,每个58元。
9 ɑ表示
58 b表示
58- ɑ表示
9 ɑ+ 58 b表示
如果ɑ = 45, b = 6,则9 ɑ+ 58 b=
3、填空练习。
(1)小红今年m 岁,陈老师的岁数比她的3倍少8岁。陈老师的岁数( )岁。如果m=12,陈老师今年是( )岁。
(2)修一条长a千米的路,如果每天修2千米。修了b天后,还剩( )千米。
(3)三个连续的自然数,最大的一个是a,那么最小的一个数是( )。
(4)长方形的宽是m米,长是宽的2倍,长方形的周长是( )米,面积是( )平方米。
(5)一种贺卡的单价是a元,小英买5张这样的贺卡。用去( )元;小明买n张这样的贺卡,付出10元,应找回( )元。
(6)每千瓦时电费0.52元,每立方米水费2元。小明家本月用了a千瓦时电和b立方米水,一共要付水电费( )元。
4、选择。
(1)小涛看一本书,第一天看了全书的20%全书有x页。还剩( )页。
A、20% x B、x -20% C、x - 20%x
(2)小刚今年a 岁,小红今年(a+5)岁,再过x年后,他们相差( )岁。
A、5 B、x C、x +5
(3)在 5+2x>10、 x+x-18、 x = 3 、11+13=4×6、 X- 0.5x = 2 等5个式子中,有( )个方程。
A、3 B、2 C、4
(4)m是奇数,n是偶数,下面结果是奇数的式子是( )。
A、3m +n B、2m+n C、2(m+n)
四、整理方程的知识
(一)师:什么是等式?什么是方程?什么叫解方程?什么叫方程的解?(老师一口气抛出几个问题,学生带着问题思考)
师随学生回答大屏幕出示方程的定义:
生齐读
出示一组式子,生判断是不是方程并说明理由。
?100-35=65??
x-13>72
x+36
4+0.7x=102
32=16×2
结合前两个算式学生用自己喜欢的表达方式来说说方程与等式的关系
我们可以用一句话概括:
生:方程一定是等式,但等式不一定是方程。(图示)
等式
方程
师:请同学们判断
1)0.5x>1是方程。( )
2)含有未知数的式子是方程。( )
3)方程是等式,等式也是方程。( )
(二)解方程。请同学们计算下面两道。
x-3.5+8=16 8x-4.8x=1.6
师总结:希望同学们能够养成做完题后自觉检查的好习惯。
下面我们就用解方程的知识来解决两道生活中的实际问题。
做完和同桌交流做法,说出根据什么等量关系解方程。
学生展示不同的做法,师小结:
等式的基本性质
1 、等式的左边和右边同时加上(或减去)同一个数,左右两边仍然相等。
2 、等式的左边和右边同时乘以(或除以)一个非0的数,左右两边仍然相等。
五、解决实际问题;
1、学生回忆用方程解决实际问题的步骤
读题,弄清题意,设未知数。
分析题意,找出数量关系式。
列方程,并解方程。
检验,写出答案。
2、完成相应的练习
(1)学校组织远足活动。原计划每小时走3.8km,3小时到达目的地。实际2.5小时走完了原定路程,平均每小时走了多少千米?
(2)一种树苗实验成活率是95%,为了保证成活380棵,至少要种多少棵树苗?
(3)小平在踢毽比赛中踢了42下,她踢毽的数量是小云的false。小云踢了多少下?
师:这节课我们一起回顾、整理了很多式与方程的知识,收获知识不是最快乐的,用我们收获的知识去解决无数的数学问题才是我们学习数学的最大乐趣。你们说对不对。那你们愿意把你们收获的知识和老师一起分享吗?
学生谈收获!
六、作业布置:(略)
七、板书设计: 式与方程的整理和复习
1、用字母表示数字
用字母表示数
2、用字母表示数量关系
式与方程
3、用字母表示计算公式
4、用字母表示运算定律
5、还可以用字母表示其它
简易方程
1、解方程
2、用方程解决实际问题
