2020-2021学年河北省石家庄市正定县八年级上学期期中数学试卷 (Word版 含解析)
文档属性
| 名称 | 2020-2021学年河北省石家庄市正定县八年级上学期期中数学试卷 (Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 368.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 00:00:00 | ||
图片预览




文档简介
2020-2021学年河北省石家庄市正定县八年级(上)期中数学试卷
一、选择题(共16个小题)
1.下列式子中是分式的是( )
A. B. C. D.
2.化简:﹣=( )
A.0 B.1 C.x D.
3.在实数,,π﹣2,,0.121 221 222 1…(两个”1”之间依次多一个“2”)中,有理数有( )
A.1个 B.2个 C.3个 D.4个
4.关于的叙述,错误的是( )
A.是有理数
B.面积为10的正方形边长是
C.是无限不循环小数
D.在数轴上可以找到表示的点
5.下列命题中是真命题的是( )
A.相等的角是对顶角
B.数轴上的点与实数一一对应
C.同旁内角互补
D.无理数就是开方开不尽的数
6.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.AB=AC B.BD=CD C.∠B=∠C D.∠BDA=∠CDA
7.分式中,a,b都扩大2倍,那么分式的值( )
A.不变 B.扩大为原来的2倍
C.扩大为原来的4倍 D.缩小为原来的
8.已知+b2+2b+1=0,则ab=( )
A.3 B.﹣3 C. D.﹣
9.如图,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小、形状完全相同的玻璃,那么他可以( )
A.带①去 B.带②去 C.带③去 D.带①和②去
10.下列二次根式计算正确的是( )
A.=±7 B.=4
C.=1﹣ D.()2=
11.若分式的值为0,则x的值为( )
A.﹣1 B.0 C.2 D.﹣1或2
12.如图所示,△ABC≌△AEF,AB=AE,有以下结论:
①AC=AE;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确的个数是( )
A.1 B.2 C.3 D.4
13.A、B两地相距48千米,一般轮胎从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为5千米/时.若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. B.
C. D.
14.若关于x的分式方程=有增根,则m的值是( )
A.﹣3 B.1 C.2 D.3
15.已知:m、n为两个连续的整数,且m<<n,以下判断正确的是( )
A.的整数部分与小数部分的差是4﹣
B.m=3
C.的小数部分是0.236
D.m+n=9
16.如图,AB=BC,AB⊥BC,过点B作直线l,过点A作AE⊥于E,过点C作CF⊥l于F,则下列说法中正确的是( )
A.AC=AE+BE B.EF=AE+EB C.AC=EB+CF D.EF=EB+CF
二、填空题(共4个小题,每小题3分,共12分.)
17.的平方根为 .
18.命题“两直线平行,同位角相等.”的逆命题是 .
19.比较大小:7 .
20.如图,已知四边形ABCD中,AB=10厘米,BC=8厘米,CD=12厘米,∠B=∠C,点E为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,当点Q的运动速度为 厘米/秒时,能够使△BEP与△CPQ全等.
三、简答题(共6个小题,共56分)
21.(1)先化简,再求值:(1﹣)÷,其中x=5.
(2)解分式方程:+2=.
22.如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
23.已知x2﹣25=0,64(y﹣1)3﹣1=0,求|x﹣4y|的值.
24.已知:两边及其夹角,线段a,c,∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.(用尺规作图,保留作图痕迹,不写作法)
请你根据所学的知识,说明尺规作图作出∠ABC=∠α,用到的是三角形全等判定定理中的 ,作出的△ABC是唯一的,依据是三角形全等判定定理中的 .
25.甲、乙两人准备整理一批新到的实验器材,若甲单独整理需要40分钟完工,若甲、乙共同整理20分钟后,乙需再单独整理10分钟才能完工.
(1)问乙单独整理多少分钟完工?
(2)若乙因工作需要,他的整理时间不超过15分钟,则甲至少整理多少分钟才能完工?
26.如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点.连接AD,以AD为一边且在AD的右侧作等腰直角三角形ADE,AD=AE,∠DAE=90°.解答下列问题:
(1)如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图乙,求证:BD=CE,BD⊥CE.
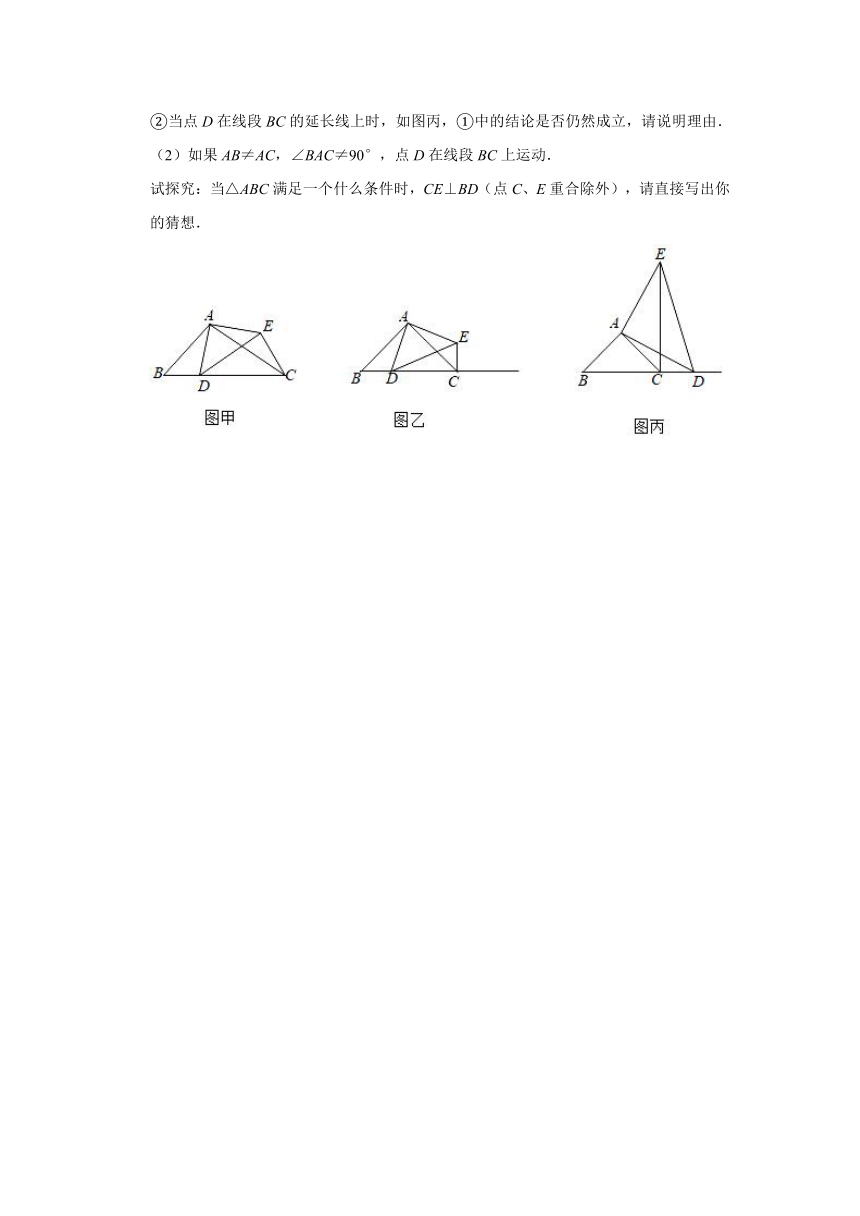
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,请说明理由.
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外),请直接写出你的猜想.
参考答案
一、选择题(共16个小题,每小题2分,共32分)
1.下列式子中是分式的是( )
A. B. C. D.
解:、、的分母中不含有字母,属于整式,的分母中含有字母,属于分式.
故选:C.
2.化简:﹣=( )
A.0 B.1 C.x D.
解:原式==x.
故选:C.
3.在实数,,π﹣2,,0.121 221 222 1…(两个”1”之间依次多一个“2”)中,有理数有( )
A.1个 B.2个 C.3个 D.4个
解:有理数有:、=﹣3,两个,
故选:B.
4.关于的叙述,错误的是( )
A.是有理数
B.面积为10的正方形边长是
C.是无限不循环小数
D.在数轴上可以找到表示的点
解:A、是无理数,原说法错误;
B、面积为10的正方形边长是,原说法正确;
C、是无理数,是无限不循环小数,原说法正确;
D、在数轴上可以找到对应的点,原说法正确;
故选:A.
5.下列命题中是真命题的是( )
A.相等的角是对顶角
B.数轴上的点与实数一一对应
C.同旁内角互补
D.无理数就是开方开不尽的数
解:A、相等的角不一定是对顶角,故此命题是假命题;
B、数轴上的点与实数一一对应,故此命题是真命题;
C、两直线平行,同旁内角互补,故此命题是假命题;
D、π2是无理数,但不是开方开不尽的数,故此命题是假命题;
故选:B.
6.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.AB=AC B.BD=CD C.∠B=∠C D.∠BDA=∠CDA
解:A、∵∠1=∠2,AD为公共边,若AB=AC,则△ABD≌△ACD(SAS);故A不符合题意;
B、∵∠1=∠2,AD为公共边,若BD=CD,不符合全等三角形判定定理,不能判定△ABD≌△ACD;故B符合题意;
C、∵∠1=∠2,AD为公共边,若∠B=∠C,则△ABD≌△ACD(AAS);故C不符合题意;
D、∵∠1=∠2,AD为公共边,若∠BDA=∠CDA,则△ABD≌△ACD(ASA);故D不符合题意.
故选:B.
7.分式中,a,b都扩大2倍,那么分式的值( )
A.不变 B.扩大为原来的2倍
C.扩大为原来的4倍 D.缩小为原来的
解:分式中,a,b都扩大2倍,
则分式的值为:=.
故选:B.
8.已知+b2+2b+1=0,则ab=( )
A.3 B.﹣3 C. D.﹣
解:∵+b2+2b+1=0,
∴+(b+1)2=0,
∴a﹣3=0,b+1=0,
解得:a=3,b=﹣1,
则ab=3﹣1=.
故选:C.
9.如图,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小、形状完全相同的玻璃,那么他可以( )
A.带①去 B.带②去 C.带③去 D.带①和②去
解:第一块,仅保留了原三角形的一个角和部分边,不符合全等三角形的判定方法;
第二块,仅保留了原三角形的一部分边,所以此块玻璃也不行;
第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故选:C.
10.下列二次根式计算正确的是( )
A.=±7 B.=4
C.=1﹣ D.()2=
解:A、原式=7,所以A选项错误;
B、原式=±4,所以B选项错误;
C、原式=﹣1,所以C选项错误;
D、原式=,所以D选项正确.
故选:D.
11.若分式的值为0,则x的值为( )
A.﹣1 B.0 C.2 D.﹣1或2
解:由题意得:x﹣2=0,且x+1≠0,
解得:x=2,
故选:C.
12.如图所示,△ABC≌△AEF,AB=AE,有以下结论:
①AC=AE;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确的个数是( )
A.1 B.2 C.3 D.4
解:∵△ABC≌△AEF,
∴BC=EF,∠BAC=∠EAF,故③正确;
∴∠EAB+∠BAF=∠FAC+∠BAF,
即∠EAB=∠FAC,故④正确;
AC与AE不是对应边,不能求出二者相等,也不能求出∠FAB=∠EAB,
故①、②错误;
故选:B.
13.A、B两地相距48千米,一般轮胎从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为5千米/时.若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. B.
C. D.
解:设该轮船在静水中的速度为x千米/时,由题意得:
+=9,
故选:A.
14.若关于x的分式方程=有增根,则m的值是( )
A.﹣3 B.1 C.2 D.3
解:去分母得:x﹣2=m,
由分式方程有增根,得到x﹣3=0,即x=3,
把x=3代入整式方程得:m=1,
故选:B.
15.已知:m、n为两个连续的整数,且m<<n,以下判断正确的是( )
A.的整数部分与小数部分的差是4﹣
B.m=3
C.的小数部分是0.236
D.m+n=9
解:∵4<5<9,
∴2<<3,
∴m=2,n=3,故选项B不符合题意,
∴m+n=5,故选项D不符合题意,
∵的整数部分为2,
∴的小数部分为﹣2,故选项C不符合题意,
∴的整数部分与小数部分的差=2﹣(﹣2)=4﹣,故选项A符合题意,
故选:A.
16.如图,AB=BC,AB⊥BC,过点B作直线l,过点A作AE⊥于E,过点C作CF⊥l于F,则下列说法中正确的是( )
A.AC=AE+BE B.EF=AE+EB C.AC=EB+CF D.EF=EB+CF
解:∵AE⊥l,CF⊥l,
∴∠AEB=∠CFB=90°.
∴∠EAB+∠EBA=90°.
又∵∠ABC=90°,
∴∠EBA+∠CBF=90°.
∴∠EAB=∠CBF.
在△AEB和△BFC中
∵∠AEB=∠CFB,∠EAB=∠CBF,AB=BC,
∴△AEB≌△BFC(AAS).
∴AE=BF,EB=CF.
∴AE+CF=EB+BF.
即EF=AE+EB.
故选:B.
二、填空题(共4个小题,每小题3分,共12分.请把答案填在题中的横线上)
17.的平方根为 ±3 .
解:∵=9
∴的平方根为±3.
故答案为:±3.
18.命题“两直线平行,同位角相等.”的逆命题是 同位角相等,两直线平行 .
解:∵原命题的条件为:两直线平行,结论为:同位角相等.
∴其逆命题为:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
19.比较大小:7 < .
解:∵7=,而<,
∴7<.
故填空结果为:<.
20.如图,已知四边形ABCD中,AB=10厘米,BC=8厘米,CD=12厘米,∠B=∠C,点E为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,当点Q的运动速度为 2或 厘米/秒时,能够使△BEP与△CPQ全等.
解:设点P运动的时间为t秒,则BP=2t,CP=8﹣2t,
∵∠B=∠C,
∴①当BE=CP=5,BP=CQ时,△BPE与△CQP全等,
此时,5=8﹣2t,
解得t=,
∴BP=CQ=3,
此时,点Q的运动速度为3÷=2(厘米/秒);
②当BE=CQ=5,BP=CP时,△BPE与△CQP全等,
此时,2t=8﹣2t,
解得t=2,
∴点Q的运动速度为5÷2=(厘米/秒);
故答案为:2或.
三、简答题(共6个小题,共56分,请写出必要的文字说明、证明过程或演算步骤)
21.(1)先化简,再求值:(1﹣)÷,其中x=5.
(2)解分式方程:+2=.
解:(1),
当x=5时,原式=;
(2)方程两边同乘(x﹣2),得:1+2(x﹣2)=x﹣1,
解得x=2,
经检验,x=2是增根.
∴原方程无解.
22.如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
【解答】(1)证明:∵BF=CE,
∴BF+FC=FC+CE,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
(2)结论:AB∥DE,AC∥DF.
理由:∵△ABC≌△DEF,
∴∠ABC=∠DEF,∠ACB=∠DFE,
∴AB∥DE,AC∥DF.
23.已知x2﹣25=0,64(y﹣1)3﹣1=0,求|x﹣4y|的值.
解:∵x2﹣25=0,
∴x2=25,
∴x=±5;
∵64(y﹣1)3﹣1=0,
∴(y﹣1)3=,
∴y﹣1=,
∴y=,
当x=5,y=时,|x﹣4y|=5﹣5=0,
当x=﹣5,y=时,|x﹣4y|=|﹣5﹣5|=10.
故|x﹣4y|的值为0或10.
24.已知:两边及其夹角,线段a,c,∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.(用尺规作图,保留作图痕迹,不写作法)
请你根据所学的知识,说明尺规作图作出∠ABC=∠α,用到的是三角形全等判定定理中的 SSS ,作出的△ABC是唯一的,依据是三角形全等判定定理中的 SAS .
解:如图,△ABC为所作;
用到的是三角形全等判定定理中的“SSS”,作出的△ABC是唯一的,依据是三角形全等判定定理中的“SAS”.
故答案为SSS,SAS.
25.甲、乙两人准备整理一批新到的实验器材,若甲单独整理需要40分钟完工,若甲、乙共同整理20分钟后,乙需再单独整理10分钟才能完工.
(1)问乙单独整理多少分钟完工?
(2)若乙因工作需要,他的整理时间不超过15分钟,则甲至少整理多少分钟才能完工?
解:(1)设乙单独整理x分钟完工,
根据题意得:+=1,
解得:x=60,
经检验,x=60是原方程的解,且符合题意.
答:乙单独整理60分钟完工.
(2)设甲整理y分钟完工,
根据题意得:+≥1,
解得:y≥30.
答:甲至少整理30分钟才能完工.
26.如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点.连接AD,以AD为一边且在AD的右侧作等腰直角三角形ADE,AD=AE,∠DAE=90°.解答下列问题:
(1)如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图乙,求证:BD=CE,BD⊥CE.
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,请说明理由.
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外),请直接写出你的猜想.
解:(1)①∵∠BAD=90°﹣∠DAC,∠CAE=90°﹣∠DAC,
∴∠BAD=∠CAE.
又 BA=CA,AD=AE,
∴△ABD≌△ACE (SAS),
∴∠ACE=∠B=45°,CE=BD,
∵∠ACB=∠B=45°,
∴∠ECB=45°+45°=90°,
即 CE⊥BD.
②当点D在BC的延长线上时,①的结论仍成立,
∵∠DAE=90°,∠BAC=90°,
∴∠DAE=∠BAC,
∴∠DAB=∠EAC,
又AB=AC,AD=AE,
∴△DAB≌△EAC(SAS),
∴CE=BD,∠ACE=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACE=45°,
∴∠BCE=∠ACB+∠ACE=90°,
即 CE⊥BD;
(2)如图丁所示,当∠BCA=45°时,CE⊥BD.
理由:过点A作AG⊥AC交BC于点G,
∴AC=AG,∠AGC=45°,
即△ACG是等腰直角三角形,
∵∠GAD+∠DAC=90°=∠CAE+∠DAC,
∴∠GAD=∠CAE,
又∵DA=EA,
∴△GAD≌△CAE(SAS),
∴∠ACE=∠AGD=45°,
∴∠BCE=∠ACB+∠ACE=90°,
即CE⊥BD.
一、选择题(共16个小题)
1.下列式子中是分式的是( )
A. B. C. D.
2.化简:﹣=( )
A.0 B.1 C.x D.
3.在实数,,π﹣2,,0.121 221 222 1…(两个”1”之间依次多一个“2”)中,有理数有( )
A.1个 B.2个 C.3个 D.4个
4.关于的叙述,错误的是( )
A.是有理数
B.面积为10的正方形边长是
C.是无限不循环小数
D.在数轴上可以找到表示的点
5.下列命题中是真命题的是( )
A.相等的角是对顶角
B.数轴上的点与实数一一对应
C.同旁内角互补
D.无理数就是开方开不尽的数
6.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.AB=AC B.BD=CD C.∠B=∠C D.∠BDA=∠CDA
7.分式中,a,b都扩大2倍,那么分式的值( )
A.不变 B.扩大为原来的2倍
C.扩大为原来的4倍 D.缩小为原来的
8.已知+b2+2b+1=0,则ab=( )
A.3 B.﹣3 C. D.﹣
9.如图,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小、形状完全相同的玻璃,那么他可以( )
A.带①去 B.带②去 C.带③去 D.带①和②去
10.下列二次根式计算正确的是( )
A.=±7 B.=4
C.=1﹣ D.()2=
11.若分式的值为0,则x的值为( )
A.﹣1 B.0 C.2 D.﹣1或2
12.如图所示,△ABC≌△AEF,AB=AE,有以下结论:
①AC=AE;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确的个数是( )
A.1 B.2 C.3 D.4
13.A、B两地相距48千米,一般轮胎从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为5千米/时.若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. B.
C. D.
14.若关于x的分式方程=有增根,则m的值是( )
A.﹣3 B.1 C.2 D.3
15.已知:m、n为两个连续的整数,且m<<n,以下判断正确的是( )
A.的整数部分与小数部分的差是4﹣
B.m=3
C.的小数部分是0.236
D.m+n=9
16.如图,AB=BC,AB⊥BC,过点B作直线l,过点A作AE⊥于E,过点C作CF⊥l于F,则下列说法中正确的是( )
A.AC=AE+BE B.EF=AE+EB C.AC=EB+CF D.EF=EB+CF
二、填空题(共4个小题,每小题3分,共12分.)
17.的平方根为 .
18.命题“两直线平行,同位角相等.”的逆命题是 .
19.比较大小:7 .
20.如图,已知四边形ABCD中,AB=10厘米,BC=8厘米,CD=12厘米,∠B=∠C,点E为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,当点Q的运动速度为 厘米/秒时,能够使△BEP与△CPQ全等.
三、简答题(共6个小题,共56分)
21.(1)先化简,再求值:(1﹣)÷,其中x=5.
(2)解分式方程:+2=.
22.如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
23.已知x2﹣25=0,64(y﹣1)3﹣1=0,求|x﹣4y|的值.
24.已知:两边及其夹角,线段a,c,∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.(用尺规作图,保留作图痕迹,不写作法)
请你根据所学的知识,说明尺规作图作出∠ABC=∠α,用到的是三角形全等判定定理中的 ,作出的△ABC是唯一的,依据是三角形全等判定定理中的 .
25.甲、乙两人准备整理一批新到的实验器材,若甲单独整理需要40分钟完工,若甲、乙共同整理20分钟后,乙需再单独整理10分钟才能完工.
(1)问乙单独整理多少分钟完工?
(2)若乙因工作需要,他的整理时间不超过15分钟,则甲至少整理多少分钟才能完工?
26.如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点.连接AD,以AD为一边且在AD的右侧作等腰直角三角形ADE,AD=AE,∠DAE=90°.解答下列问题:
(1)如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图乙,求证:BD=CE,BD⊥CE.
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,请说明理由.
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外),请直接写出你的猜想.
参考答案
一、选择题(共16个小题,每小题2分,共32分)
1.下列式子中是分式的是( )
A. B. C. D.
解:、、的分母中不含有字母,属于整式,的分母中含有字母,属于分式.
故选:C.
2.化简:﹣=( )
A.0 B.1 C.x D.
解:原式==x.
故选:C.
3.在实数,,π﹣2,,0.121 221 222 1…(两个”1”之间依次多一个“2”)中,有理数有( )
A.1个 B.2个 C.3个 D.4个
解:有理数有:、=﹣3,两个,
故选:B.
4.关于的叙述,错误的是( )
A.是有理数
B.面积为10的正方形边长是
C.是无限不循环小数
D.在数轴上可以找到表示的点
解:A、是无理数,原说法错误;
B、面积为10的正方形边长是,原说法正确;
C、是无理数,是无限不循环小数,原说法正确;
D、在数轴上可以找到对应的点,原说法正确;
故选:A.
5.下列命题中是真命题的是( )
A.相等的角是对顶角
B.数轴上的点与实数一一对应
C.同旁内角互补
D.无理数就是开方开不尽的数
解:A、相等的角不一定是对顶角,故此命题是假命题;
B、数轴上的点与实数一一对应,故此命题是真命题;
C、两直线平行,同旁内角互补,故此命题是假命题;
D、π2是无理数,但不是开方开不尽的数,故此命题是假命题;
故选:B.
6.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.AB=AC B.BD=CD C.∠B=∠C D.∠BDA=∠CDA
解:A、∵∠1=∠2,AD为公共边,若AB=AC,则△ABD≌△ACD(SAS);故A不符合题意;
B、∵∠1=∠2,AD为公共边,若BD=CD,不符合全等三角形判定定理,不能判定△ABD≌△ACD;故B符合题意;
C、∵∠1=∠2,AD为公共边,若∠B=∠C,则△ABD≌△ACD(AAS);故C不符合题意;
D、∵∠1=∠2,AD为公共边,若∠BDA=∠CDA,则△ABD≌△ACD(ASA);故D不符合题意.
故选:B.
7.分式中,a,b都扩大2倍,那么分式的值( )
A.不变 B.扩大为原来的2倍
C.扩大为原来的4倍 D.缩小为原来的
解:分式中,a,b都扩大2倍,
则分式的值为:=.
故选:B.
8.已知+b2+2b+1=0,则ab=( )
A.3 B.﹣3 C. D.﹣
解:∵+b2+2b+1=0,
∴+(b+1)2=0,
∴a﹣3=0,b+1=0,
解得:a=3,b=﹣1,
则ab=3﹣1=.
故选:C.
9.如图,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小、形状完全相同的玻璃,那么他可以( )
A.带①去 B.带②去 C.带③去 D.带①和②去
解:第一块,仅保留了原三角形的一个角和部分边,不符合全等三角形的判定方法;
第二块,仅保留了原三角形的一部分边,所以此块玻璃也不行;
第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故选:C.
10.下列二次根式计算正确的是( )
A.=±7 B.=4
C.=1﹣ D.()2=
解:A、原式=7,所以A选项错误;
B、原式=±4,所以B选项错误;
C、原式=﹣1,所以C选项错误;
D、原式=,所以D选项正确.
故选:D.
11.若分式的值为0,则x的值为( )
A.﹣1 B.0 C.2 D.﹣1或2
解:由题意得:x﹣2=0,且x+1≠0,
解得:x=2,
故选:C.
12.如图所示,△ABC≌△AEF,AB=AE,有以下结论:
①AC=AE;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确的个数是( )
A.1 B.2 C.3 D.4
解:∵△ABC≌△AEF,
∴BC=EF,∠BAC=∠EAF,故③正确;
∴∠EAB+∠BAF=∠FAC+∠BAF,
即∠EAB=∠FAC,故④正确;
AC与AE不是对应边,不能求出二者相等,也不能求出∠FAB=∠EAB,
故①、②错误;
故选:B.
13.A、B两地相距48千米,一般轮胎从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为5千米/时.若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. B.
C. D.
解:设该轮船在静水中的速度为x千米/时,由题意得:
+=9,
故选:A.
14.若关于x的分式方程=有增根,则m的值是( )
A.﹣3 B.1 C.2 D.3
解:去分母得:x﹣2=m,
由分式方程有增根,得到x﹣3=0,即x=3,
把x=3代入整式方程得:m=1,
故选:B.
15.已知:m、n为两个连续的整数,且m<<n,以下判断正确的是( )
A.的整数部分与小数部分的差是4﹣
B.m=3
C.的小数部分是0.236
D.m+n=9
解:∵4<5<9,
∴2<<3,
∴m=2,n=3,故选项B不符合题意,
∴m+n=5,故选项D不符合题意,
∵的整数部分为2,
∴的小数部分为﹣2,故选项C不符合题意,
∴的整数部分与小数部分的差=2﹣(﹣2)=4﹣,故选项A符合题意,
故选:A.
16.如图,AB=BC,AB⊥BC,过点B作直线l,过点A作AE⊥于E,过点C作CF⊥l于F,则下列说法中正确的是( )
A.AC=AE+BE B.EF=AE+EB C.AC=EB+CF D.EF=EB+CF
解:∵AE⊥l,CF⊥l,
∴∠AEB=∠CFB=90°.
∴∠EAB+∠EBA=90°.
又∵∠ABC=90°,
∴∠EBA+∠CBF=90°.
∴∠EAB=∠CBF.
在△AEB和△BFC中
∵∠AEB=∠CFB,∠EAB=∠CBF,AB=BC,
∴△AEB≌△BFC(AAS).
∴AE=BF,EB=CF.
∴AE+CF=EB+BF.
即EF=AE+EB.
故选:B.
二、填空题(共4个小题,每小题3分,共12分.请把答案填在题中的横线上)
17.的平方根为 ±3 .
解:∵=9
∴的平方根为±3.
故答案为:±3.
18.命题“两直线平行,同位角相等.”的逆命题是 同位角相等,两直线平行 .
解:∵原命题的条件为:两直线平行,结论为:同位角相等.
∴其逆命题为:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
19.比较大小:7 < .
解:∵7=,而<,
∴7<.
故填空结果为:<.
20.如图,已知四边形ABCD中,AB=10厘米,BC=8厘米,CD=12厘米,∠B=∠C,点E为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,当点Q的运动速度为 2或 厘米/秒时,能够使△BEP与△CPQ全等.
解:设点P运动的时间为t秒,则BP=2t,CP=8﹣2t,
∵∠B=∠C,
∴①当BE=CP=5,BP=CQ时,△BPE与△CQP全等,
此时,5=8﹣2t,
解得t=,
∴BP=CQ=3,
此时,点Q的运动速度为3÷=2(厘米/秒);
②当BE=CQ=5,BP=CP时,△BPE与△CQP全等,
此时,2t=8﹣2t,
解得t=2,
∴点Q的运动速度为5÷2=(厘米/秒);
故答案为:2或.
三、简答题(共6个小题,共56分,请写出必要的文字说明、证明过程或演算步骤)
21.(1)先化简,再求值:(1﹣)÷,其中x=5.
(2)解分式方程:+2=.
解:(1),
当x=5时,原式=;
(2)方程两边同乘(x﹣2),得:1+2(x﹣2)=x﹣1,
解得x=2,
经检验,x=2是增根.
∴原方程无解.
22.如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
【解答】(1)证明:∵BF=CE,
∴BF+FC=FC+CE,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
(2)结论:AB∥DE,AC∥DF.
理由:∵△ABC≌△DEF,
∴∠ABC=∠DEF,∠ACB=∠DFE,
∴AB∥DE,AC∥DF.
23.已知x2﹣25=0,64(y﹣1)3﹣1=0,求|x﹣4y|的值.
解:∵x2﹣25=0,
∴x2=25,
∴x=±5;
∵64(y﹣1)3﹣1=0,
∴(y﹣1)3=,
∴y﹣1=,
∴y=,
当x=5,y=时,|x﹣4y|=5﹣5=0,
当x=﹣5,y=时,|x﹣4y|=|﹣5﹣5|=10.
故|x﹣4y|的值为0或10.
24.已知:两边及其夹角,线段a,c,∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.(用尺规作图,保留作图痕迹,不写作法)
请你根据所学的知识,说明尺规作图作出∠ABC=∠α,用到的是三角形全等判定定理中的 SSS ,作出的△ABC是唯一的,依据是三角形全等判定定理中的 SAS .
解:如图,△ABC为所作;
用到的是三角形全等判定定理中的“SSS”,作出的△ABC是唯一的,依据是三角形全等判定定理中的“SAS”.
故答案为SSS,SAS.
25.甲、乙两人准备整理一批新到的实验器材,若甲单独整理需要40分钟完工,若甲、乙共同整理20分钟后,乙需再单独整理10分钟才能完工.
(1)问乙单独整理多少分钟完工?
(2)若乙因工作需要,他的整理时间不超过15分钟,则甲至少整理多少分钟才能完工?
解:(1)设乙单独整理x分钟完工,
根据题意得:+=1,
解得:x=60,
经检验,x=60是原方程的解,且符合题意.
答:乙单独整理60分钟完工.
(2)设甲整理y分钟完工,
根据题意得:+≥1,
解得:y≥30.
答:甲至少整理30分钟才能完工.
26.如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点.连接AD,以AD为一边且在AD的右侧作等腰直角三角形ADE,AD=AE,∠DAE=90°.解答下列问题:
(1)如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图乙,求证:BD=CE,BD⊥CE.
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,请说明理由.
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外),请直接写出你的猜想.
解:(1)①∵∠BAD=90°﹣∠DAC,∠CAE=90°﹣∠DAC,
∴∠BAD=∠CAE.
又 BA=CA,AD=AE,
∴△ABD≌△ACE (SAS),
∴∠ACE=∠B=45°,CE=BD,
∵∠ACB=∠B=45°,
∴∠ECB=45°+45°=90°,
即 CE⊥BD.
②当点D在BC的延长线上时,①的结论仍成立,
∵∠DAE=90°,∠BAC=90°,
∴∠DAE=∠BAC,
∴∠DAB=∠EAC,
又AB=AC,AD=AE,
∴△DAB≌△EAC(SAS),
∴CE=BD,∠ACE=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACE=45°,
∴∠BCE=∠ACB+∠ACE=90°,
即 CE⊥BD;
(2)如图丁所示,当∠BCA=45°时,CE⊥BD.
理由:过点A作AG⊥AC交BC于点G,
∴AC=AG,∠AGC=45°,
即△ACG是等腰直角三角形,
∵∠GAD+∠DAC=90°=∠CAE+∠DAC,
∴∠GAD=∠CAE,
又∵DA=EA,
∴△GAD≌△CAE(SAS),
∴∠ACE=∠AGD=45°,
∴∠BCE=∠ACB+∠ACE=90°,
即CE⊥BD.
同课章节目录
