2020年人教版七年级数学上册课时训练:4.3.2《角的比较与运算》(Word版 含解析)
文档属性
| 名称 | 2020年人教版七年级数学上册课时训练:4.3.2《角的比较与运算》(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 154.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 17:33:01 | ||
图片预览



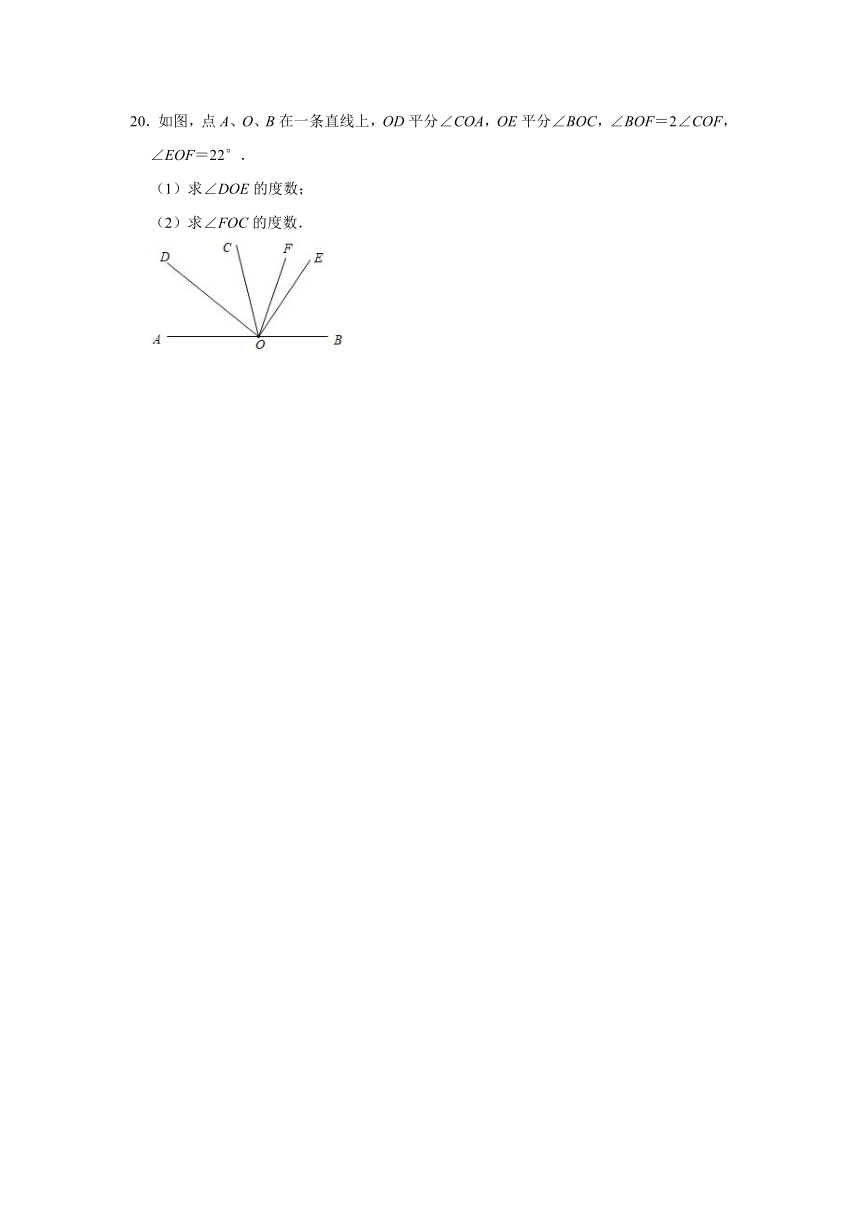
文档简介
2020年人教版七年级数学上册课时训练:4.3.2《角的比较与运算》
一.选择题
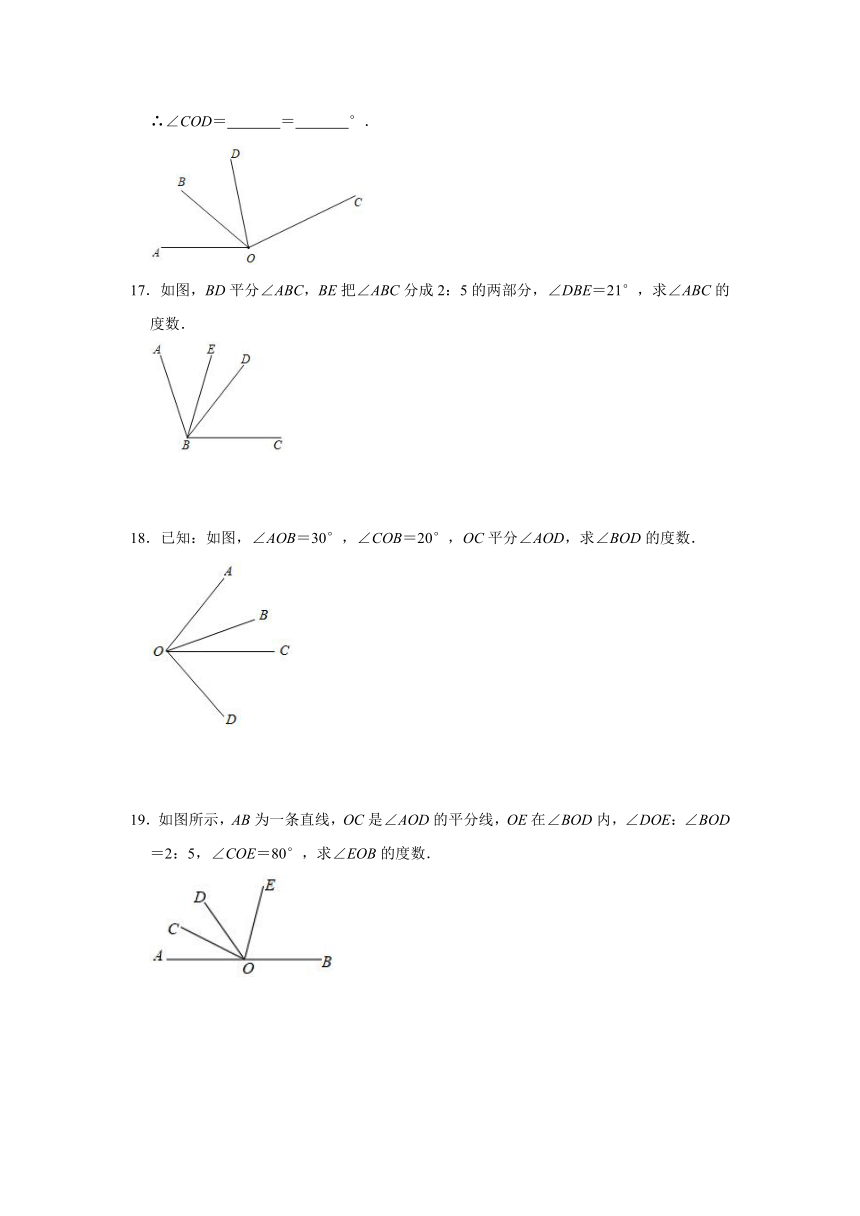
1.如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB=( )
A.40°
B.60°
C.120°
D.135°
2.如图,OC是∠AOB的平分线,∠BOD=∠DOC,∠BOD=18°,则∠AOD的度数为( )
A.72°
B.80°
C.90°
D.108°
3.如图,∠AOD=60°,∠AOB:∠BOC=1:4,OD平分∠BOC,则∠AOC的度数为( )
A.20°
B.80°
C.100°
D.120°
4.如图,已知∠AOB:∠BOC=2:3,∠AOC=75°,那么∠AOB=( )
A.20°
B.30°
C.35°
D.45°
5.如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是( )
A.∠COD=∠AOB
B.∠AOD=∠AOB
C.∠BOD=∠AOD
D.∠BOC=∠AOD
6.如图,点O在直线AE上,OC平分∠AOE,∠DOB是直角.若∠1=25°,那么∠AOB的度数是( )
A.65°
B.25°
C.90°
D.115°
7.如图,∠BOD=118°,∠COD是直角,OC平分∠AOB,则∠AOB的度数是( )
A.48°
B.56°
C.60°
D.32°
8.已知∠AOB=60°,∠AOC=∠AOB,射线OD平分∠BOC,则∠COD的度数为( )
A.20°
B.40°
C.20°或30°
D.20°或40°
二.填空题
9.已知∠AOB=40°,OC是∠AOB的平分线,则∠AOC等于
.
10.已知:如图,点O为直线AB上一点,OC是∠AOB的平分线,OD在∠BOC内看图填空(选填“<”、“>”或“=”):∠AOD
∠BOC
11.如图,点O在直线AB上,OC是∠AOD的平分线.若∠BOD=50°,则∠AOC的度数为
.
12.如图所示,OB是∠AOC的平分线,OC是∠AOD的平分线,若∠COD=76°,那么∠AOD=
,∠BOC=
.
13.以∠AOB的顶点O为端点引射线OP,使∠AOP:∠BOP=3:2,若∠AOB=20°,∠AOP的度数为
.
14.若∠AOB=45°,∠BOC=75°,OD平分∠AOB,OE平分∠BOC,则∠DOE的度数为
.
三.解答题
15.已知:如图,∠AOB=30°,∠COB=20°,OC平分∠AOD.求∠COD的度数.
∵∠AOB=30°,∠COB=20°(已知),
∴∠AOC=∠
+∠
=
°.
∵OC平分∠AOD,
∴∠AOC=∠
(角平分线定义).
∴∠COD=
°.
16.如图,已知∠AOB=40°,∠BOC=3∠AOB,OD平分∠AOC,求∠COD的度数.
解:∵∠BOC=3∠
,∠AOB=40°,
∴∠BOC=
°
∴∠AOC=
+
∴∠AOC=160°
∵OD平分∠AOC
∴∠COD=
=
°.
17.如图,BD平分∠ABC,BE把∠ABC分成2:5的两部分,∠DBE=21°,求∠ABC的度数.
18.已知:如图,∠AOB=30°,∠COB=20°,OC平分∠AOD,求∠BOD的度数.
19.如图所示,AB为一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE:∠BOD=2:5,∠COE=80°,求∠EOB的度数.
20.如图,点A、O、B在一条直线上,OD平分∠COA,OE平分∠BOC,∠BOF=2∠COF,∠EOF=22°.
(1)求∠DOE的度数;
(2)求∠FOC的度数.
参考答案
一.选择题
1.解:设∠AOC=x,则∠BOC=2x,则∠AOD=1.5x.
∵∠AOD﹣∠AOC=∠COD,
∴1.5x﹣x=20°,解得:x=40°.
∴∠AOB=3x=120°.
故选:C.
2.解:设∠DOB=k,
∵∠BOD=∠DOC,
∴∠BOC=2k,
∵OC是∠AOB的平分线,
∴∠COA=∠BOC=2k,
∴∠AOD=∠DOB+∠BOC+∠COA=5k,
∵∠BOD=18°,
∴∠AOD=5×18°=90°,
故选:C.
3.解:∵∠AOB:∠BOC=1:4,
∴设∠AOB为x,∠BOC为4x,
∵OD平分∠BOC,
∴∠BOD=∠BOC=2x,
∵∠AOD=60°,
∴x+2x=60°,
∴x=20°,
4x=80°,
∴∠AOC=∠AOB+∠BOC=20°+80°=100°,
故选:C.
4.解:∵∠AOB:∠BOC=2:3,∠AOC=75°,
∴∠AOB=∠AOC=×75°=30°,
故选:B.
5.解:∵OC是∠AOB的平分线,OD是∠BOC的平分线,
∴∠BOC=∠AOC=∠AOB,∠BOD=∠AOC=∠BOC,
∴∠BOC=∠AOD,
故选:D.
6.解:∵点O在直线AE上,OC平分∠AOE,
∴∠AOC=∠COE=90°,
∵∠DOB是直角,∠1=25°,
∴∠BOC=∠DOB﹣∠1=90°﹣25°=65°,
∵∠AOB+∠BOC=∠AOC=90°
∴∠AOB=90°﹣∠BOC=90°﹣65°=25°.
故选:B.
7.解:∵OC平分∠AOB,
∴∠AOB=2∠AOC=2∠BOC,
∵∠COD是直角,
∴∠COD=90°,
∵∠BOD=118°,
∴∠BOC=∠BOD﹣∠COD=118°﹣90°=28°,
∴∠AOB=2∠BOC=56°.
故选:B.
8.解:当OC在∠AOB内时,如图1,
则∠BOC=∠AOB﹣∠AOC=60°﹣,
∴∠COD=∠BOC=20°;
当OC在∠AOB外时,如图2,
则∠BOC=∠AOB+∠AOC=60°+,
∴∠COD=∠BOC=40°.
综上,∠COD=20°或40°.
故选:D.
二.填空题
9.解:∵OC是∠AOB的平分线,∠AOB=40°,
∴∠AOC=∠AOB=×40°=20°,
故答案为:20°.
10.解:∵点O为直线AB上一点,OC是∠AOB的平分线,
∴∠AOC=∠BOC=90°,
∵∠AOD=∠DOC+∠AOC>90°,
∴∠AOD>∠BOC.
故答案为:>.
11.解:∵点O在直线AB上,
∴∠AOD+∠BOD=180°,
∵∠BOD=50°,
∴∠AOD=180°﹣∠BOD=180°﹣50°=130°,
∵OC是∠AOD的平分线,
∴∠AOC=∠AOD=×130°=65°,
故答案为:65°.
12.解:∵OC是∠AOD的平分线,
∴∠AOC=∠COD=76°,
∠AOD=2∠COD=2×76°=152°,
∵OB是∠AOC的平分线,
∴∠BOC=∠AOC=×76°=38°.
故答案为152°;38°.
13.解:如图1,当射线OP在∠AOB的内部时,设∠AOP=3x,则∠BOP=2x,
∵∠AOB=∠AOP+∠BOP=5x=20°,
解得:x=4°,
则∠AOP=12°;
如图2,当射线OP在∠AOB的外部时,设∠AOP=3x,则∠BOP=2x,
∵∠AOP=∠AOB+∠BOP,
又∵∠AOB=20°,
∴3x=20°+2x,
解得:x=20°,
则∠AOP=60°.
故∠AOP的度数为12°或60°.
故答案为:12°或60°.
14.解:如图1,
∵∠AOB=45°,
∴∠BOD=22.5°,
∵∠BOC=75°,
∴∠BOE=37.5°,
∴∠DOE=22.5°+37.5°=60°;
如图2,∵∠AOB=45°,
∴∠BOD=22.5°,
∵∠BOC=75°,
∴∠BOE=37.5°,
∴∠DOE=37.5°﹣22.5°=15°,
故答案为:60°或15°.
三.解答题
15.证明:∵∠AOB=30°,∠COB=20°(已知),
∴∠AOC=∠AOB+∠COB=50°
∵OC平分∠AOD(已知),
∴∠AOC=∠COD=50°(角平分线定义
)
故答案为:AOB;COB;50;COD;50.
16.解:∵∠BOC=3∠AOB,∠AOB=40°,
∴∠BOC=120°,
∴∠AOC=∠AOB+∠BOC
∴∠AOC=160°
∵OD平分∠AOC
∴∠COD=∠AOC=80°.
故答案为AOB;120;∠AOB,∠BOC;∠AOC,80°.
17.解:设∠ABE=2x°,
得2x+21=5x﹣21,
解得x=14,
∴∠ABC=14°×7=98°.
∴∠ABC的度数是98°.
18.解:∵∠AOB=30°,∠COB=20°,
∴∠AOC=∠AOB+∠BOC=30°+20°=50°,
∵OC平分∠AOD,
∴∠AOC=∠COD=50°,
∴∠BOD=∠BOC+∠COD=20°+50°=70°.
19.解:如图,设∠DOE=2x,
∵∠DOE:∠BOD=2:5,
∴∠BOE=3x,
又∵OC是∠AOD的平分线,∠COE=80°,
∴∠AOC=∠COD=80°﹣2x
2×(80°﹣2x)+5x=180°,
解得x=20°
∴∠BOE=3x=3×20°=60°.
故答案为:60°.
20.解:(1)∵OD平分∠COA,OE平分∠BOC,
∴,,
∴;
(2)设∠FOC=x,
∵OE平分∠BOC,∠BOF=2∠COF,
∴2x﹣22°=x+22°,
解得x=44°.
一.选择题
1.如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB=( )
A.40°
B.60°
C.120°
D.135°
2.如图,OC是∠AOB的平分线,∠BOD=∠DOC,∠BOD=18°,则∠AOD的度数为( )
A.72°
B.80°
C.90°
D.108°
3.如图,∠AOD=60°,∠AOB:∠BOC=1:4,OD平分∠BOC,则∠AOC的度数为( )
A.20°
B.80°
C.100°
D.120°
4.如图,已知∠AOB:∠BOC=2:3,∠AOC=75°,那么∠AOB=( )
A.20°
B.30°
C.35°
D.45°
5.如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是( )
A.∠COD=∠AOB
B.∠AOD=∠AOB
C.∠BOD=∠AOD
D.∠BOC=∠AOD
6.如图,点O在直线AE上,OC平分∠AOE,∠DOB是直角.若∠1=25°,那么∠AOB的度数是( )
A.65°
B.25°
C.90°
D.115°
7.如图,∠BOD=118°,∠COD是直角,OC平分∠AOB,则∠AOB的度数是( )
A.48°
B.56°
C.60°
D.32°
8.已知∠AOB=60°,∠AOC=∠AOB,射线OD平分∠BOC,则∠COD的度数为( )
A.20°
B.40°
C.20°或30°
D.20°或40°
二.填空题
9.已知∠AOB=40°,OC是∠AOB的平分线,则∠AOC等于
.
10.已知:如图,点O为直线AB上一点,OC是∠AOB的平分线,OD在∠BOC内看图填空(选填“<”、“>”或“=”):∠AOD
∠BOC
11.如图,点O在直线AB上,OC是∠AOD的平分线.若∠BOD=50°,则∠AOC的度数为
.
12.如图所示,OB是∠AOC的平分线,OC是∠AOD的平分线,若∠COD=76°,那么∠AOD=
,∠BOC=
.
13.以∠AOB的顶点O为端点引射线OP,使∠AOP:∠BOP=3:2,若∠AOB=20°,∠AOP的度数为
.
14.若∠AOB=45°,∠BOC=75°,OD平分∠AOB,OE平分∠BOC,则∠DOE的度数为
.
三.解答题
15.已知:如图,∠AOB=30°,∠COB=20°,OC平分∠AOD.求∠COD的度数.
∵∠AOB=30°,∠COB=20°(已知),
∴∠AOC=∠
+∠
=
°.
∵OC平分∠AOD,
∴∠AOC=∠
(角平分线定义).
∴∠COD=
°.
16.如图,已知∠AOB=40°,∠BOC=3∠AOB,OD平分∠AOC,求∠COD的度数.
解:∵∠BOC=3∠
,∠AOB=40°,
∴∠BOC=
°
∴∠AOC=
+
∴∠AOC=160°
∵OD平分∠AOC
∴∠COD=
=
°.
17.如图,BD平分∠ABC,BE把∠ABC分成2:5的两部分,∠DBE=21°,求∠ABC的度数.
18.已知:如图,∠AOB=30°,∠COB=20°,OC平分∠AOD,求∠BOD的度数.
19.如图所示,AB为一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE:∠BOD=2:5,∠COE=80°,求∠EOB的度数.
20.如图,点A、O、B在一条直线上,OD平分∠COA,OE平分∠BOC,∠BOF=2∠COF,∠EOF=22°.
(1)求∠DOE的度数;
(2)求∠FOC的度数.
参考答案
一.选择题
1.解:设∠AOC=x,则∠BOC=2x,则∠AOD=1.5x.
∵∠AOD﹣∠AOC=∠COD,
∴1.5x﹣x=20°,解得:x=40°.
∴∠AOB=3x=120°.
故选:C.
2.解:设∠DOB=k,
∵∠BOD=∠DOC,
∴∠BOC=2k,
∵OC是∠AOB的平分线,
∴∠COA=∠BOC=2k,
∴∠AOD=∠DOB+∠BOC+∠COA=5k,
∵∠BOD=18°,
∴∠AOD=5×18°=90°,
故选:C.
3.解:∵∠AOB:∠BOC=1:4,
∴设∠AOB为x,∠BOC为4x,
∵OD平分∠BOC,
∴∠BOD=∠BOC=2x,
∵∠AOD=60°,
∴x+2x=60°,
∴x=20°,
4x=80°,
∴∠AOC=∠AOB+∠BOC=20°+80°=100°,
故选:C.
4.解:∵∠AOB:∠BOC=2:3,∠AOC=75°,
∴∠AOB=∠AOC=×75°=30°,
故选:B.
5.解:∵OC是∠AOB的平分线,OD是∠BOC的平分线,
∴∠BOC=∠AOC=∠AOB,∠BOD=∠AOC=∠BOC,
∴∠BOC=∠AOD,
故选:D.
6.解:∵点O在直线AE上,OC平分∠AOE,
∴∠AOC=∠COE=90°,
∵∠DOB是直角,∠1=25°,
∴∠BOC=∠DOB﹣∠1=90°﹣25°=65°,
∵∠AOB+∠BOC=∠AOC=90°
∴∠AOB=90°﹣∠BOC=90°﹣65°=25°.
故选:B.
7.解:∵OC平分∠AOB,
∴∠AOB=2∠AOC=2∠BOC,
∵∠COD是直角,
∴∠COD=90°,
∵∠BOD=118°,
∴∠BOC=∠BOD﹣∠COD=118°﹣90°=28°,
∴∠AOB=2∠BOC=56°.
故选:B.
8.解:当OC在∠AOB内时,如图1,
则∠BOC=∠AOB﹣∠AOC=60°﹣,
∴∠COD=∠BOC=20°;
当OC在∠AOB外时,如图2,
则∠BOC=∠AOB+∠AOC=60°+,
∴∠COD=∠BOC=40°.
综上,∠COD=20°或40°.
故选:D.
二.填空题
9.解:∵OC是∠AOB的平分线,∠AOB=40°,
∴∠AOC=∠AOB=×40°=20°,
故答案为:20°.
10.解:∵点O为直线AB上一点,OC是∠AOB的平分线,
∴∠AOC=∠BOC=90°,
∵∠AOD=∠DOC+∠AOC>90°,
∴∠AOD>∠BOC.
故答案为:>.
11.解:∵点O在直线AB上,
∴∠AOD+∠BOD=180°,
∵∠BOD=50°,
∴∠AOD=180°﹣∠BOD=180°﹣50°=130°,
∵OC是∠AOD的平分线,
∴∠AOC=∠AOD=×130°=65°,
故答案为:65°.
12.解:∵OC是∠AOD的平分线,
∴∠AOC=∠COD=76°,
∠AOD=2∠COD=2×76°=152°,
∵OB是∠AOC的平分线,
∴∠BOC=∠AOC=×76°=38°.
故答案为152°;38°.
13.解:如图1,当射线OP在∠AOB的内部时,设∠AOP=3x,则∠BOP=2x,
∵∠AOB=∠AOP+∠BOP=5x=20°,
解得:x=4°,
则∠AOP=12°;
如图2,当射线OP在∠AOB的外部时,设∠AOP=3x,则∠BOP=2x,
∵∠AOP=∠AOB+∠BOP,
又∵∠AOB=20°,
∴3x=20°+2x,
解得:x=20°,
则∠AOP=60°.
故∠AOP的度数为12°或60°.
故答案为:12°或60°.
14.解:如图1,
∵∠AOB=45°,
∴∠BOD=22.5°,
∵∠BOC=75°,
∴∠BOE=37.5°,
∴∠DOE=22.5°+37.5°=60°;
如图2,∵∠AOB=45°,
∴∠BOD=22.5°,
∵∠BOC=75°,
∴∠BOE=37.5°,
∴∠DOE=37.5°﹣22.5°=15°,
故答案为:60°或15°.
三.解答题
15.证明:∵∠AOB=30°,∠COB=20°(已知),
∴∠AOC=∠AOB+∠COB=50°
∵OC平分∠AOD(已知),
∴∠AOC=∠COD=50°(角平分线定义
)
故答案为:AOB;COB;50;COD;50.
16.解:∵∠BOC=3∠AOB,∠AOB=40°,
∴∠BOC=120°,
∴∠AOC=∠AOB+∠BOC
∴∠AOC=160°
∵OD平分∠AOC
∴∠COD=∠AOC=80°.
故答案为AOB;120;∠AOB,∠BOC;∠AOC,80°.
17.解:设∠ABE=2x°,
得2x+21=5x﹣21,
解得x=14,
∴∠ABC=14°×7=98°.
∴∠ABC的度数是98°.
18.解:∵∠AOB=30°,∠COB=20°,
∴∠AOC=∠AOB+∠BOC=30°+20°=50°,
∵OC平分∠AOD,
∴∠AOC=∠COD=50°,
∴∠BOD=∠BOC+∠COD=20°+50°=70°.
19.解:如图,设∠DOE=2x,
∵∠DOE:∠BOD=2:5,
∴∠BOE=3x,
又∵OC是∠AOD的平分线,∠COE=80°,
∴∠AOC=∠COD=80°﹣2x
2×(80°﹣2x)+5x=180°,
解得x=20°
∴∠BOE=3x=3×20°=60°.
故答案为:60°.
20.解:(1)∵OD平分∠COA,OE平分∠BOC,
∴,,
∴;
(2)设∠FOC=x,
∵OE平分∠BOC,∠BOF=2∠COF,
∴2x﹣22°=x+22°,
解得x=44°.
