圆周角学案第一课时

24.1.4圆周角（第一课时）
一、复习回顾：
1、圆心角的定义： 。
圆心角、弧、弦定理： 。
推论1： 。
推论2： 。
在定理和推论中注意不能丢掉 这个前提。
二、讲授新课：P84 阅读观察
1、圆周角定义： 。
圆周角有两个特征：① 。② 。
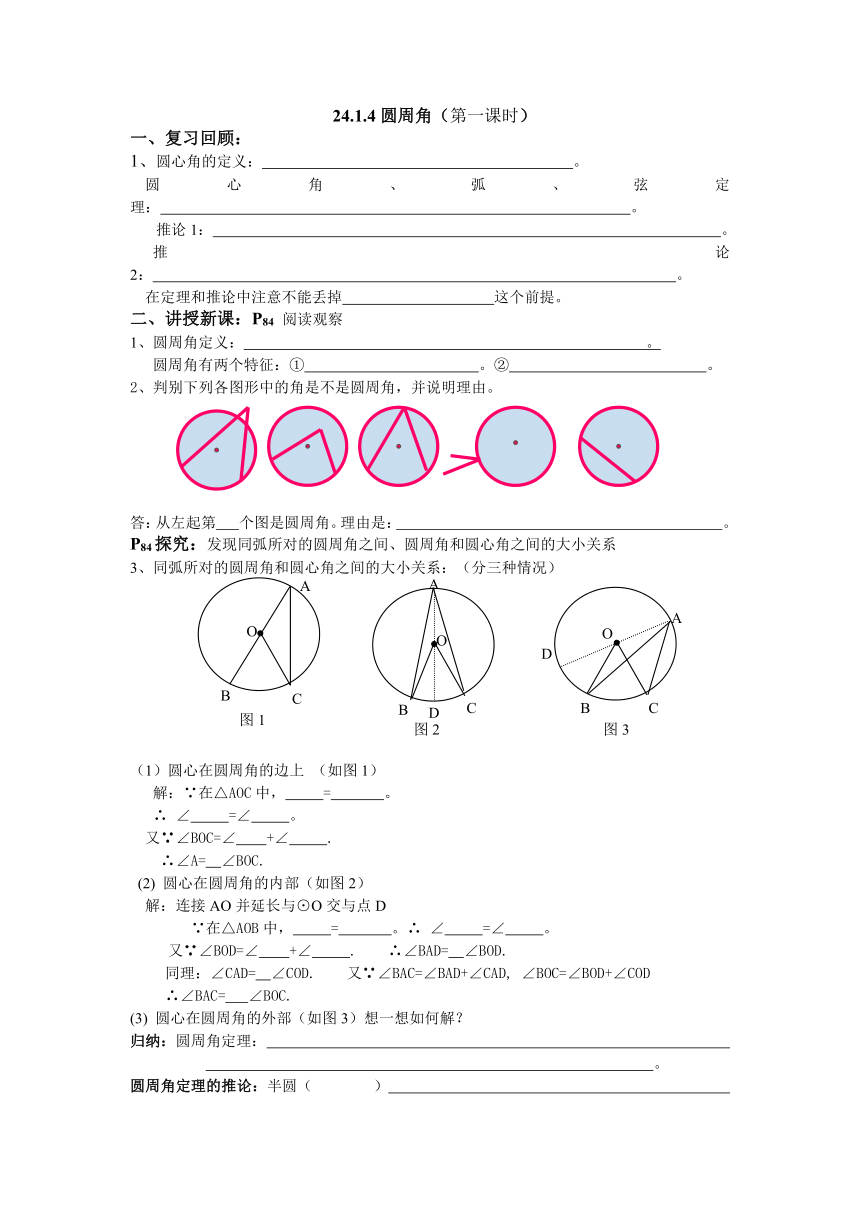
2、判别下列各图形中的角是不是圆周角，并说明理由。
答：从左起第 个图是圆周角。理由是： 。
P84探究：发现同弧所对的圆周角之间、圆周角和圆心角之间的大小关系
3、同弧所对的圆周角和圆心角之间的大小关系：（分三种情况）
（1）圆心在圆周角的边上 （如图1）
解：∵在△AOC中， = 。
∴ ∠ =∠ 。
又∵∠BOC=∠ +∠ .
∴∠A= ∠BOC.
(2) 圆心在圆周角的内部（如图2）
解：连接AO并延长与⊙O交与点D
∵在△AOB中， = 。∴ ∠ =∠ 。
又∵∠BOD=∠ +∠ . ∴∠BAD= ∠BOD.
同理：∠CAD= ∠COD. 又∵∠BAC=∠BAD+∠CAD, ∠BOC=∠BOD+∠COD
∴∠BAC= ∠BOC.
(3) 圆心在圆周角的外部（如图3）想一想如何解？
归纳：圆周角定理：
。
圆周角定理的推论：半圆（ ）
。
由圆周角定理可知：在同圆或等圆中，如果两个圆周角相等，那么
三、例题学习：如图, ⊙O的直径AB为10cm,弦AC为6 cm, ∠ACB的平
分线交⊙O于D,
求BC,AD,BD的长。
分析：求BC的长关键是确定△ABC是 三角形。
即∠ =900.(根据： )
由 定理可求BC。要求AD和BD只要得到
∠ACD=∠ （根据： ）
因此可得AD=BD (理由： )
再由 定理求的AD和BD。
四、课堂练习：
1、如图2：试找出图甲中所有相等的圆周角
2、在圆中一条弧所对的圆心角和圆周角分别为(2x + 100)0和(5x – 30)0则这条弧
所对的圆心角的度数为 、圆周角的度数为 。
3、图3中互余的圆周角共有……………………………（ ）
A、4对 B、6对 C、8对 D、10对
4、如图5，求∠1＋∠2＋∠3＋∠4＋∠5= .
5．如图6，的直径，弦
，则弦的长为（ ）
A． B． C． D．
6.如图，⊙O的半径为1，AB是⊙O 的一条弦，
且AB=，则弦AB所对圆周角的度数为（ ）
（A）30° （B）60°（C）30°或150° （D）60°或120°
7.如图，内接于，若，则的大小为（ ）
A． 　　　B．　　 C．　　　D．
8.的直径，弦，则弦的长为（ ）
A． B． C． D．
9.如图23.1.12，AB是⊙O的直径，∠A＝80°．求∠ABC的度数．
A
O
B
C
图1
D
A
A
B
C
O
B
C
O
图2
图3
D
3
图2
1
2
4
5
6
7
8
图3
O
1
2
3
4
5
6
7
8
图6
C
A
B
O
E
D
C
A
B
O