苏科版九年级数学下册6.1---6.2测试题(含答案)
文档属性
| 名称 | 苏科版九年级数学下册6.1---6.2测试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 412.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 21:14:39 | ||
图片预览




文档简介
6.1图上距离与实际距离-
一、选择题
1、在比例尺是1:40000的地图上,若某条道路长约为5cm,则它的实际长度约为(
)
A.0.2km
B.2km
C.20km
D.200km
2、下列各组线段中,长度成比例的是(
).
(A)2cm,3cm,4cm,1cm
(B)1.5cm,2.5cm,4.5cm,6.5cm
(C)1.1cm,2.2cm,3.3cm,4.4cm
(D)1cm,2cm,3cm,4cm
3、若==(a≠0),则等于(
)
A.3
B.5
C.7
D.8
4、如果2x=3y(x、y均不为0),那么下列各式中正确的是(
)
A.
B.
C.
D.
5、如果==(b+d+f≠0),那么正确的结果是(
)
A.
=
B.=
C.
==
D.==
6、已知2x=3y=6z=﹣2017,则x+y+z+2017是(
)
A.正数
B.负数
C.零
D.无法确定
7、若=,=,则的值为(
)
A.
B.
C.
D.
8、如图,如果=成立,下列结论中不正确的是(
)
A.=
B.=
C.=
D.=
9、(2020秋?宜兴月考)已知=k,则k的值是( )
A.﹣1
B.2
C.﹣1或2
D.无法确定
二、填空题
10、在比例尺为1:5000的地图上,量得甲、乙两地的距离为25cm,
则甲、乙两地间的实际距离是
11、若(a+2b):(a-2b)=9:5,则a:b=________
12、已知,则
13、若,则m的值是
14、若a=4,c=9,求a、c的比例中项b=_________.
15、线段2
cm、8
cm的比例中项为_________cm.
三、解答题
16、若==,且3x+2y-z=14,求x,y,z的值.
17、已知有三条长分别为1cm、4cm、8cm的线段,请再添加一条线段,使这四条线段成比例,
求所添加线段的长.
18、已知a,b,c为△ABC的三边长,且a+b+c=60,==,试求△ABC的面积.
19、如图,在Rt△ABC中,CD是斜边AB上的高线,试猜想线段AC,AB,CD,BC是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不能,请说明理由.
6.1图上距离与实际距离-苏科版九年级数学下册
巩固训练(答案)
一、选择题
1、在比例尺是1:40000的地图上,若某条道路长约为5cm,则它的实际长度约为(
B
)
A.0.2km
B.2km
C.20km
D.200km
2、下列各组线段中,长度成比例的是(
D
).
(A)2cm,3cm,4cm,1cm
(B)1.5cm,2.5cm,4.5cm,6.5cm
(C)1.1cm,2.2cm,3.3cm,4.4cm
(D)1cm,2cm,3cm,4cm
3、若==(a≠0),则等于(
B
)
A.3
B.5
C.7
D.8
4、如果2x=3y(x、y均不为0),那么下列各式中正确的是(
A
)
A.
B.
C.
D.
5、如果==(b+d+f≠0),那么正确的结果是(
B
)
A.
=
B.=
C.
==
D.==
6、已知2x=3y=6z=﹣2017,则x+y+z+2017是(
C
)
A.正数
B.负数
C.零
D.无法确定
7、若=,=,则的值为(
B
)
A.
B.
C.
D.
8、如图,如果=成立,下列结论中不正确的是(
C
)
A.=
B.=
C.=
D.=
9、(2020秋?宜兴月考)已知=k,则k的值是( )
A.﹣1
B.2
C.﹣1或2
D.无法确定
【解析】由k,得b+c=ak ①,a+c=bk ②,a+b=ck ③,
①+②+③,得2(a+b+c)=k(a+b+c),
移项,得2(a+b+c)﹣k(a+b+c)=0,
因式分解,得(a+b+c)(2﹣k)=0
a+b+c=0或k=2,
a+b+c=0时,b+c=﹣a,
故选:C.
二、填空题
10、在比例尺为1:5000的地图上,量得甲、乙两地的距离为25cm,
则甲、乙两地间的实际距离是
1.25km
11、若(a+2b):(a-2b)=9:5,则a:b=___7_____
12、已知,则
4
13、若,则m的值是
﹣1或
14、若a=4,c=9,求a、c的比例中项b=_________.
解析:∵b是a、c的比例中项,
∴,
∴
15、线段2
cm、8
cm的比例中项为__4_______cm.
三、解答题
16、若==,且3x+2y-z=14,求x,y,z的值.
解:设===k,则x=2k,y=3k,z=5k.
∵3x+2y-z=14,∴6k+6k-5k=14.
解得k=2.
∴x=4,y=6,z=10
17、已知有三条长分别为1cm、4cm、8cm的线段,请再添加一条线段,使这四条线段成比例,
求所添加线段的长.
解析:设所添加线段的长为xcm,则
①1:4=8:x,解得x=32;
②1:4=x:8,解得x=2
③1:8=4:x,解得x=32
④1:8=x:4,解得x=0.5
⑤1:x=4:8,解得x=2
⑥1:x=8:4,解得x=0.5
综上所述,所添加线段的长为0.5cm或2cm或32cm.
18、已知a,b,c为△ABC的三边长,且a+b+c=60,==,试求△ABC的面积.
解:由=====5,
可得a=15,b=20,c=25.
又∵152+202=252,即a2+b2=c2,∴△ABC是直角三角形.
∴S△ABC=×15×20=150.
19、如图,在Rt△ABC中,CD是斜边AB上的高线,试猜想线段AC,AB,CD,BC是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不能,请说明理由.
解析:线段AC,AB,CD,BC对应成比例,且.
验证如下:根据三角形的面积公式,得,
∴,即
6.2
黄金分割
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
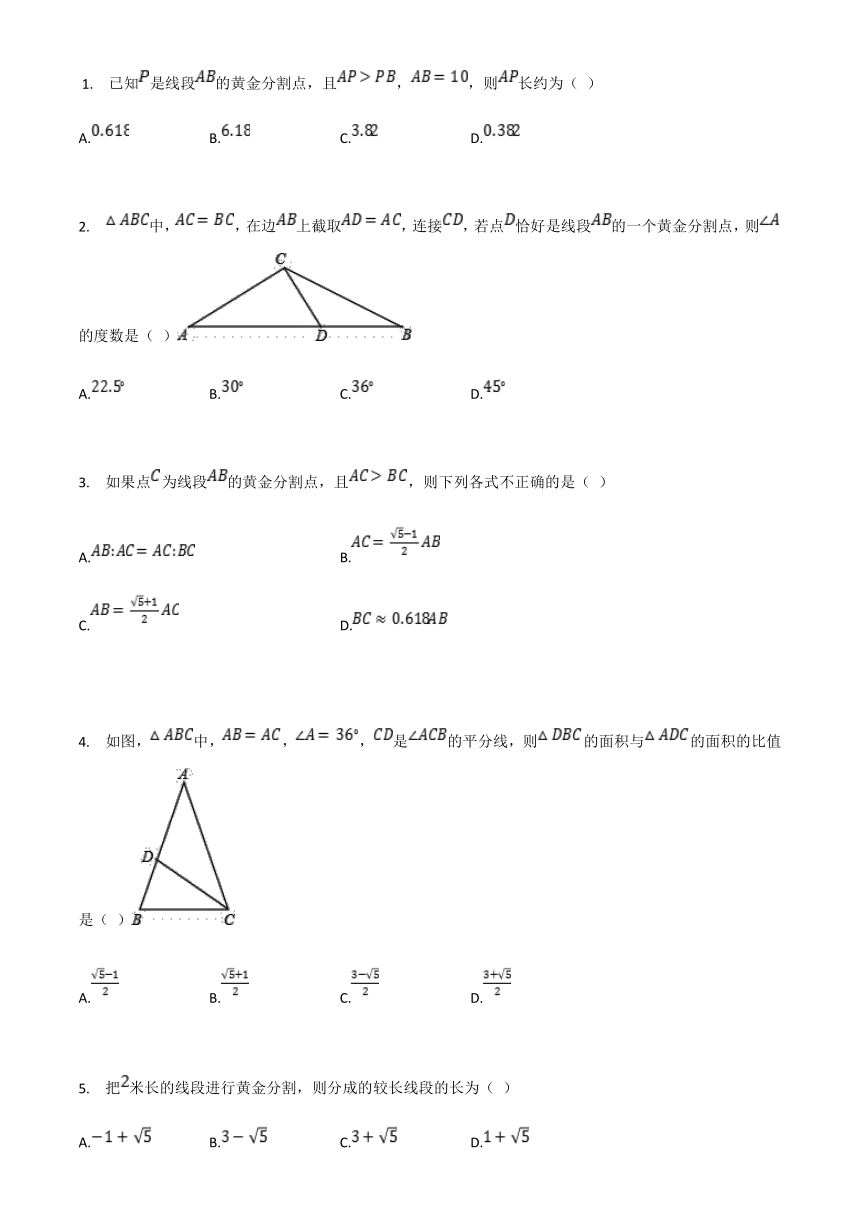
?1.
已知是线段的黄金分割点,且,,则长约为(
)
A.
B.
C.
D.
?
2.
中,,在边上截取,连接,若点恰好是线段的一个黄金分割点,则的度数是(
)
A.
B.
C.
D.
?
3.
如果点为线段的黄金分割点,且,则下列各式不正确的是(
)
A.
B.
C.
D.
?
4.
如图,中,,,是的平分线,则的面积与的面积的比值是(
)
A.
B.
C.
D.
?
5.
把米长的线段进行黄金分割,则分成的较长线段的长为(
)
A.
B.
C.
D.
?
6.
现已知线段,点是线段的黄金分割点,,那么线段的长约为(
)
A.
B.
C.
D.
?
7.
已知点是线段的黄金分割点,,若,则
A.
B.
C.
D.
?
8.
已知点是线段的黄金分割点,且,则下列各式的值不等于的是(
)
A.
B.
C.
D.
?
9.
顶角为的等腰三角形称为黄金三角形,如图,五边形的条边相等,个内角相等,则图中共有黄金三角形的个数是(
)
A.
B.
C.
D.
?
10.
如图所示,顶角为的等腰三角形,其底边与腰之比等于,这样的三角形叫做黄金三角形.已知,为第一个黄金三角形,为第二个黄金三角形,为第三个黄金三角形,以此类推,第个黄金三角形的周长为(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
是长为的线段的黄金分割点,则________.
?
12.
如图,中,是的黄金分割点,过点作交于,若,则________.
?
13.
美是一种感觉,当人体下半身长与身高的比值越接近时,越给人一种美感.李老师身高厘米,下半身长与身高的比值是,为了尽可能达到好的效果,她应穿的高跟鞋的高度大约为________(结果精确到).
?
14.
美是一种感觉,一矩形的长为,宽为,当矩形的宽与长的比值是黄金比值时,这样的矩形给人一种美感.试问长不变,宽增加________时,给人的美感效果最佳.
?
15.
有些植物茎上,相邻两张叶子成的角,这种角度使植物通风和采光的效果最佳,这一度数与________角成黄金比例.
?
16.
要使点是线段的黄金分割点,那么线段、、应满足的数量关系是________.
?
17.
若点是的黄金分割点,则线段、、满足关系式________.
?
18.
如果点是线段的黄金分割点,且,那么的值为________.
?
19.
已知线段,点是靠近点的的黄金分割点.点是靠近点的黄金分割点,则________.
?
20.
报幕员在台上时,若站在黄金分割点处,会显得活泼而生动,已知舞台长米,那么报幕员要至少走________米报幕.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
如图,在五角星图形中,,,两点都是的黄金分割点,,求的长.
?
22.
(1)已知线段的长为,是的黄金分割点,求的长;
(2)求作线段的黄金分割点,要求尺规作图,且使.
?
23.
在中,为边上一点,过点作交与点,连接.若.
点是线段的黄金分割点吗?请说明你的理由;
已知,计算黄金比.
?
24.
如图,在线段上有一点,若,则称点为的黄金分割点,现已知,点是线段的黄金分割点,求的长.
?
25.
在中,,,把像这样的三角形叫做黄金三角形.
(1)请你设计三种不同的分法,将黄金三角形分割成三个等腰三角形,使得分割成的三角形中含有两个黄金三角形(画图工具不限,要求画出分割线段;标出能够说明不同分法所得三角形的内角度数,不要求写画法,不要求证明.分别画在图,图,图中)
注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.
(2)如图中,平分交于,取的中点,连接?并延长交?的延长线于.试判断与之间的数量关系?只需说明结果,不用证明.
答:与之间的数量关系是________.
?
26.
如图,是的直径,点在上,,过点作直线分别交直线和于点、,连接,,.
(1)求的度数;
(2)我们把有一个内角等于的等腰三角形称为黄金三角形.它的腰长与底边长的比(或者底边长与腰长的比)等于黄金分割比.
①写出图中所有的黄金三角形,选一个说明理由;
②求弦的长;
③在直线或上是否存在点(点、除外),使是黄金三角形?若存在,画出点,简要说明画出点的方法(不要求证明);若不存在,说明理由.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:由于为线段的黄金分割点,
且是较长线段;
则.
故选.
2.
【答案】
C
【解答】
解:∵
点是线段的一个黄金分割点,
∴
,
∵
,
∴
,
即,
而,
∴
,
∴
,
设,则,,
∴
,
而,
∴
,
∴
,解得,
即.
故选:.
3.
【答案】
D
【解答】
解:∵
,
∴
是较长的线段,
根据黄金分割的定义可知:,,,.
故选.
4.
【答案】
A
【解答】
解:设,.
∵
中,,,
∴
.
∵
是角平分线,
∴
.
∴
,
∴
.
∵
,,
∴
.
∴
,
即,
,
(负值舍去).
则.
∵
与底边分别为,时,高度相等,
∴
的面积与的面积的比值是:.
故选:.
5.
【答案】
A
【解答】
把米长的线段进行黄金分割,分成的较长线段的长,
6.
【答案】
A
【解答】
解:∵
点是线段的黄金分割点,
∴
.
故选:.
7.
【答案】
C
【解答】
解:当时,
,
,
故选.
8.
【答案】
C
【解答】
解:∵
点是线段的黄金分割点,且,
∴
,
设,则,,
∴
;
;
;
.
故选.
9.
【答案】
D
【解答】
解:根据题意,得
图中的黄金三角形有、、、、、、、、、、、、、、,,,,,,共个.
故选
10.
【答案】
C
【解答】
解:∵
,
∴
的周长为;
的周长为;
的周长为;
依此类推,第个黄金三角形的周长为;
故选:.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:∵
点是线段的黄金分割点,
∴
,
∵
,
∴
.
故答案为:.
12.
【答案】
【解答】
解:∵
,
∴
,
∴
,
∵
是的黄金分割点,
∴
,
∴
,
∴
,
∴
.
故答案为.
13.
【答案】
【解答】
解:根据已知条件得下半身长是,
设需要穿的高跟鞋是,
则根据黄金分割的定义得:,
解得:.
故答案为.
14.
【答案】
【解答】
解:设宽增加,
根据题意得,
解得,
即长不变,宽增加时,给人的美感效果最佳.
故答案为.
15.
【答案】
或
【解答】
解:,
,,
所以与或的角成黄金比例.
故答案为或.
16.
【答案】
【解答】
解:∵
点是线段的黄金分割点,
∴
.
故答案为.
17.
【答案】
【解答】
解:∵
点是的黄金分割点,
∴
.
故答案为.
18.
【答案】
【解答】
∵
点是线段的黄金分割点,且,
∴
,
19.
【答案】
【解答】
解:由题意得,,,
∴
.
故答案为:.
20.
【答案】
【解答】
解:报幕员要走的路程为:(米).
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:∵
、两点都是的黄金分割点,
∴
,
∴
,
∵
,
∴
,
而,
∴
,
∴
.
【解答】
解:∵
、两点都是的黄金分割点,
∴
,
∴
,
∵
,
∴
,
而,
∴
,
∴
.
22.
【答案】
解:(1)由于为线段的黄金分割点,
则,
或;
(2)如图,点是线段的一个黄金分割点.
【解答】
解:(1)由于为线段的黄金分割点,
则,
或;
(2)如图,点是线段的一个黄金分割点.
23.
【答案】
解:点是线段的黄金分割点.
证明:∵
,
,
∴
,
∴
.
又,
∴
.
∴
,
即,
又,
∴
∴
为线段的黄金分割点;
由知,,
即,
∴
,
即,
,
,
.
所以黄金比为.
【解答】
解:点是线段的黄金分割点.
证明:∵
,
,
∴
,
∴
.
又,
∴
.
∴
,
即,
又,
∴
∴
为线段的黄金分割点;
由知,,
即,
∴
,
即,
,
,
.
所以黄金比为.
24.
【答案】
解:∵
为线段的黄金分割点,且,为较长线段,
∴
.
【解答】
解:∵
为线段的黄金分割点,且,为较长线段,
∴
.
25.
【答案】
解:(1)
(2)
【解答】
解:(1)
(2)
26.
【答案】
解:(1)∵
是的直径,,
∴
,
则,,
设,则,,
又,∴
,
∴
,.
∴
.
(2)①有三个:,,.
∵
,,
∴
是黄金三角形;
∵
,.
∴
是黄金三角形;
∵
,
∴
;
又,
∴
.
∴
,
∴
是黄金三角形;
②∵
是黄金三角形,
∴
,
∵
,
∴
,
∵
,,
∴
;
③存在,有三个符合条件的点、、,
如图所示,
ⅰ以为底边的黄金三角形:作的垂直平分线分别交直线、得到点、;
ⅱ以为腰的黄金三角形:点与点重合.
【解答】
解:(1)∵
是的直径,,
∴
,
则,,
设,则,,
又,∴
,
∴
,.
∴
.
(2)①有三个:,,.
∵
,,
∴
是黄金三角形;
∵
,.
∴
是黄金三角形;
∵
,
∴
;
又,
∴
.
∴
,
∴
是黄金三角形;
②∵
是黄金三角形,
∴
,
∵
,
∴
,
∵
,,
∴
;
③存在,有三个符合条件的点、、,
如图所示,
ⅰ以为底边的黄金三角形:作的垂直平分线分别交直线、得到点、;
ⅱ以为腰的黄金三角形:点与点重合
一、选择题
1、在比例尺是1:40000的地图上,若某条道路长约为5cm,则它的实际长度约为(
)
A.0.2km
B.2km
C.20km
D.200km
2、下列各组线段中,长度成比例的是(
).
(A)2cm,3cm,4cm,1cm
(B)1.5cm,2.5cm,4.5cm,6.5cm
(C)1.1cm,2.2cm,3.3cm,4.4cm
(D)1cm,2cm,3cm,4cm
3、若==(a≠0),则等于(
)
A.3
B.5
C.7
D.8
4、如果2x=3y(x、y均不为0),那么下列各式中正确的是(
)
A.
B.
C.
D.
5、如果==(b+d+f≠0),那么正确的结果是(
)
A.
=
B.=
C.
==
D.==
6、已知2x=3y=6z=﹣2017,则x+y+z+2017是(
)
A.正数
B.负数
C.零
D.无法确定
7、若=,=,则的值为(
)
A.
B.
C.
D.
8、如图,如果=成立,下列结论中不正确的是(
)
A.=
B.=
C.=
D.=
9、(2020秋?宜兴月考)已知=k,则k的值是( )
A.﹣1
B.2
C.﹣1或2
D.无法确定
二、填空题
10、在比例尺为1:5000的地图上,量得甲、乙两地的距离为25cm,
则甲、乙两地间的实际距离是
11、若(a+2b):(a-2b)=9:5,则a:b=________
12、已知,则
13、若,则m的值是
14、若a=4,c=9,求a、c的比例中项b=_________.
15、线段2
cm、8
cm的比例中项为_________cm.
三、解答题
16、若==,且3x+2y-z=14,求x,y,z的值.
17、已知有三条长分别为1cm、4cm、8cm的线段,请再添加一条线段,使这四条线段成比例,
求所添加线段的长.
18、已知a,b,c为△ABC的三边长,且a+b+c=60,==,试求△ABC的面积.
19、如图,在Rt△ABC中,CD是斜边AB上的高线,试猜想线段AC,AB,CD,BC是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不能,请说明理由.
6.1图上距离与实际距离-苏科版九年级数学下册
巩固训练(答案)
一、选择题
1、在比例尺是1:40000的地图上,若某条道路长约为5cm,则它的实际长度约为(
B
)
A.0.2km
B.2km
C.20km
D.200km
2、下列各组线段中,长度成比例的是(
D
).
(A)2cm,3cm,4cm,1cm
(B)1.5cm,2.5cm,4.5cm,6.5cm
(C)1.1cm,2.2cm,3.3cm,4.4cm
(D)1cm,2cm,3cm,4cm
3、若==(a≠0),则等于(
B
)
A.3
B.5
C.7
D.8
4、如果2x=3y(x、y均不为0),那么下列各式中正确的是(
A
)
A.
B.
C.
D.
5、如果==(b+d+f≠0),那么正确的结果是(
B
)
A.
=
B.=
C.
==
D.==
6、已知2x=3y=6z=﹣2017,则x+y+z+2017是(
C
)
A.正数
B.负数
C.零
D.无法确定
7、若=,=,则的值为(
B
)
A.
B.
C.
D.
8、如图,如果=成立,下列结论中不正确的是(
C
)
A.=
B.=
C.=
D.=
9、(2020秋?宜兴月考)已知=k,则k的值是( )
A.﹣1
B.2
C.﹣1或2
D.无法确定
【解析】由k,得b+c=ak ①,a+c=bk ②,a+b=ck ③,
①+②+③,得2(a+b+c)=k(a+b+c),
移项,得2(a+b+c)﹣k(a+b+c)=0,
因式分解,得(a+b+c)(2﹣k)=0
a+b+c=0或k=2,
a+b+c=0时,b+c=﹣a,
故选:C.
二、填空题
10、在比例尺为1:5000的地图上,量得甲、乙两地的距离为25cm,
则甲、乙两地间的实际距离是
1.25km
11、若(a+2b):(a-2b)=9:5,则a:b=___7_____
12、已知,则
4
13、若,则m的值是
﹣1或
14、若a=4,c=9,求a、c的比例中项b=_________.
解析:∵b是a、c的比例中项,
∴,
∴
15、线段2
cm、8
cm的比例中项为__4_______cm.
三、解答题
16、若==,且3x+2y-z=14,求x,y,z的值.
解:设===k,则x=2k,y=3k,z=5k.
∵3x+2y-z=14,∴6k+6k-5k=14.
解得k=2.
∴x=4,y=6,z=10
17、已知有三条长分别为1cm、4cm、8cm的线段,请再添加一条线段,使这四条线段成比例,
求所添加线段的长.
解析:设所添加线段的长为xcm,则
①1:4=8:x,解得x=32;
②1:4=x:8,解得x=2
③1:8=4:x,解得x=32
④1:8=x:4,解得x=0.5
⑤1:x=4:8,解得x=2
⑥1:x=8:4,解得x=0.5
综上所述,所添加线段的长为0.5cm或2cm或32cm.
18、已知a,b,c为△ABC的三边长,且a+b+c=60,==,试求△ABC的面积.
解:由=====5,
可得a=15,b=20,c=25.
又∵152+202=252,即a2+b2=c2,∴△ABC是直角三角形.
∴S△ABC=×15×20=150.
19、如图,在Rt△ABC中,CD是斜边AB上的高线,试猜想线段AC,AB,CD,BC是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不能,请说明理由.
解析:线段AC,AB,CD,BC对应成比例,且.
验证如下:根据三角形的面积公式,得,
∴,即
6.2
黄金分割
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
已知是线段的黄金分割点,且,,则长约为(
)
A.
B.
C.
D.
?
2.
中,,在边上截取,连接,若点恰好是线段的一个黄金分割点,则的度数是(
)
A.
B.
C.
D.
?
3.
如果点为线段的黄金分割点,且,则下列各式不正确的是(
)
A.
B.
C.
D.
?
4.
如图,中,,,是的平分线,则的面积与的面积的比值是(
)
A.
B.
C.
D.
?
5.
把米长的线段进行黄金分割,则分成的较长线段的长为(
)
A.
B.
C.
D.
?
6.
现已知线段,点是线段的黄金分割点,,那么线段的长约为(
)
A.
B.
C.
D.
?
7.
已知点是线段的黄金分割点,,若,则
A.
B.
C.
D.
?
8.
已知点是线段的黄金分割点,且,则下列各式的值不等于的是(
)
A.
B.
C.
D.
?
9.
顶角为的等腰三角形称为黄金三角形,如图,五边形的条边相等,个内角相等,则图中共有黄金三角形的个数是(
)
A.
B.
C.
D.
?
10.
如图所示,顶角为的等腰三角形,其底边与腰之比等于,这样的三角形叫做黄金三角形.已知,为第一个黄金三角形,为第二个黄金三角形,为第三个黄金三角形,以此类推,第个黄金三角形的周长为(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
是长为的线段的黄金分割点,则________.
?
12.
如图,中,是的黄金分割点,过点作交于,若,则________.
?
13.
美是一种感觉,当人体下半身长与身高的比值越接近时,越给人一种美感.李老师身高厘米,下半身长与身高的比值是,为了尽可能达到好的效果,她应穿的高跟鞋的高度大约为________(结果精确到).
?
14.
美是一种感觉,一矩形的长为,宽为,当矩形的宽与长的比值是黄金比值时,这样的矩形给人一种美感.试问长不变,宽增加________时,给人的美感效果最佳.
?
15.
有些植物茎上,相邻两张叶子成的角,这种角度使植物通风和采光的效果最佳,这一度数与________角成黄金比例.
?
16.
要使点是线段的黄金分割点,那么线段、、应满足的数量关系是________.
?
17.
若点是的黄金分割点,则线段、、满足关系式________.
?
18.
如果点是线段的黄金分割点,且,那么的值为________.
?
19.
已知线段,点是靠近点的的黄金分割点.点是靠近点的黄金分割点,则________.
?
20.
报幕员在台上时,若站在黄金分割点处,会显得活泼而生动,已知舞台长米,那么报幕员要至少走________米报幕.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
如图,在五角星图形中,,,两点都是的黄金分割点,,求的长.
?
22.
(1)已知线段的长为,是的黄金分割点,求的长;
(2)求作线段的黄金分割点,要求尺规作图,且使.
?
23.
在中,为边上一点,过点作交与点,连接.若.
点是线段的黄金分割点吗?请说明你的理由;
已知,计算黄金比.
?
24.
如图,在线段上有一点,若,则称点为的黄金分割点,现已知,点是线段的黄金分割点,求的长.
?
25.
在中,,,把像这样的三角形叫做黄金三角形.
(1)请你设计三种不同的分法,将黄金三角形分割成三个等腰三角形,使得分割成的三角形中含有两个黄金三角形(画图工具不限,要求画出分割线段;标出能够说明不同分法所得三角形的内角度数,不要求写画法,不要求证明.分别画在图,图,图中)
注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.
(2)如图中,平分交于,取的中点,连接?并延长交?的延长线于.试判断与之间的数量关系?只需说明结果,不用证明.
答:与之间的数量关系是________.
?
26.
如图,是的直径,点在上,,过点作直线分别交直线和于点、,连接,,.
(1)求的度数;
(2)我们把有一个内角等于的等腰三角形称为黄金三角形.它的腰长与底边长的比(或者底边长与腰长的比)等于黄金分割比.
①写出图中所有的黄金三角形,选一个说明理由;
②求弦的长;
③在直线或上是否存在点(点、除外),使是黄金三角形?若存在,画出点,简要说明画出点的方法(不要求证明);若不存在,说明理由.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:由于为线段的黄金分割点,
且是较长线段;
则.
故选.
2.
【答案】
C
【解答】
解:∵
点是线段的一个黄金分割点,
∴
,
∵
,
∴
,
即,
而,
∴
,
∴
,
设,则,,
∴
,
而,
∴
,
∴
,解得,
即.
故选:.
3.
【答案】
D
【解答】
解:∵
,
∴
是较长的线段,
根据黄金分割的定义可知:,,,.
故选.
4.
【答案】
A
【解答】
解:设,.
∵
中,,,
∴
.
∵
是角平分线,
∴
.
∴
,
∴
.
∵
,,
∴
.
∴
,
即,
,
(负值舍去).
则.
∵
与底边分别为,时,高度相等,
∴
的面积与的面积的比值是:.
故选:.
5.
【答案】
A
【解答】
把米长的线段进行黄金分割,分成的较长线段的长,
6.
【答案】
A
【解答】
解:∵
点是线段的黄金分割点,
∴
.
故选:.
7.
【答案】
C
【解答】
解:当时,
,
,
故选.
8.
【答案】
C
【解答】
解:∵
点是线段的黄金分割点,且,
∴
,
设,则,,
∴
;
;
;
.
故选.
9.
【答案】
D
【解答】
解:根据题意,得
图中的黄金三角形有、、、、、、、、、、、、、、,,,,,,共个.
故选
10.
【答案】
C
【解答】
解:∵
,
∴
的周长为;
的周长为;
的周长为;
依此类推,第个黄金三角形的周长为;
故选:.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:∵
点是线段的黄金分割点,
∴
,
∵
,
∴
.
故答案为:.
12.
【答案】
【解答】
解:∵
,
∴
,
∴
,
∵
是的黄金分割点,
∴
,
∴
,
∴
,
∴
.
故答案为.
13.
【答案】
【解答】
解:根据已知条件得下半身长是,
设需要穿的高跟鞋是,
则根据黄金分割的定义得:,
解得:.
故答案为.
14.
【答案】
【解答】
解:设宽增加,
根据题意得,
解得,
即长不变,宽增加时,给人的美感效果最佳.
故答案为.
15.
【答案】
或
【解答】
解:,
,,
所以与或的角成黄金比例.
故答案为或.
16.
【答案】
【解答】
解:∵
点是线段的黄金分割点,
∴
.
故答案为.
17.
【答案】
【解答】
解:∵
点是的黄金分割点,
∴
.
故答案为.
18.
【答案】
【解答】
∵
点是线段的黄金分割点,且,
∴
,
19.
【答案】
【解答】
解:由题意得,,,
∴
.
故答案为:.
20.
【答案】
【解答】
解:报幕员要走的路程为:(米).
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:∵
、两点都是的黄金分割点,
∴
,
∴
,
∵
,
∴
,
而,
∴
,
∴
.
【解答】
解:∵
、两点都是的黄金分割点,
∴
,
∴
,
∵
,
∴
,
而,
∴
,
∴
.
22.
【答案】
解:(1)由于为线段的黄金分割点,
则,
或;
(2)如图,点是线段的一个黄金分割点.
【解答】
解:(1)由于为线段的黄金分割点,
则,
或;
(2)如图,点是线段的一个黄金分割点.
23.
【答案】
解:点是线段的黄金分割点.
证明:∵
,
,
∴
,
∴
.
又,
∴
.
∴
,
即,
又,
∴
∴
为线段的黄金分割点;
由知,,
即,
∴
,
即,
,
,
.
所以黄金比为.
【解答】
解:点是线段的黄金分割点.
证明:∵
,
,
∴
,
∴
.
又,
∴
.
∴
,
即,
又,
∴
∴
为线段的黄金分割点;
由知,,
即,
∴
,
即,
,
,
.
所以黄金比为.
24.
【答案】
解:∵
为线段的黄金分割点,且,为较长线段,
∴
.
【解答】
解:∵
为线段的黄金分割点,且,为较长线段,
∴
.
25.
【答案】
解:(1)
(2)
【解答】
解:(1)
(2)
26.
【答案】
解:(1)∵
是的直径,,
∴
,
则,,
设,则,,
又,∴
,
∴
,.
∴
.
(2)①有三个:,,.
∵
,,
∴
是黄金三角形;
∵
,.
∴
是黄金三角形;
∵
,
∴
;
又,
∴
.
∴
,
∴
是黄金三角形;
②∵
是黄金三角形,
∴
,
∵
,
∴
,
∵
,,
∴
;
③存在,有三个符合条件的点、、,
如图所示,
ⅰ以为底边的黄金三角形:作的垂直平分线分别交直线、得到点、;
ⅱ以为腰的黄金三角形:点与点重合.
【解答】
解:(1)∵
是的直径,,
∴
,
则,,
设,则,,
又,∴
,
∴
,.
∴
.
(2)①有三个:,,.
∵
,,
∴
是黄金三角形;
∵
,.
∴
是黄金三角形;
∵
,
∴
;
又,
∴
.
∴
,
∴
是黄金三角形;
②∵
是黄金三角形,
∴
,
∵
,
∴
,
∵
,,
∴
;
③存在,有三个符合条件的点、、,
如图所示,
ⅰ以为底边的黄金三角形:作的垂直平分线分别交直线、得到点、;
ⅱ以为腰的黄金三角形:点与点重合
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
