1.2充分条件与必要条件-人教A版高中数学选修2-1课件(25张PPT)
文档属性
| 名称 | 1.2充分条件与必要条件-人教A版高中数学选修2-1课件(25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览








文档简介
1.2.1充分条件与
必要条件
原命题
若p则q
逆否命题
若?q则?p
否命题
若?p则?q
逆命题
若q则p
互逆
互逆
互 否
互 否
互为 逆否
1、命题:
可以判断真假的陈述句,可写成:若p则q。
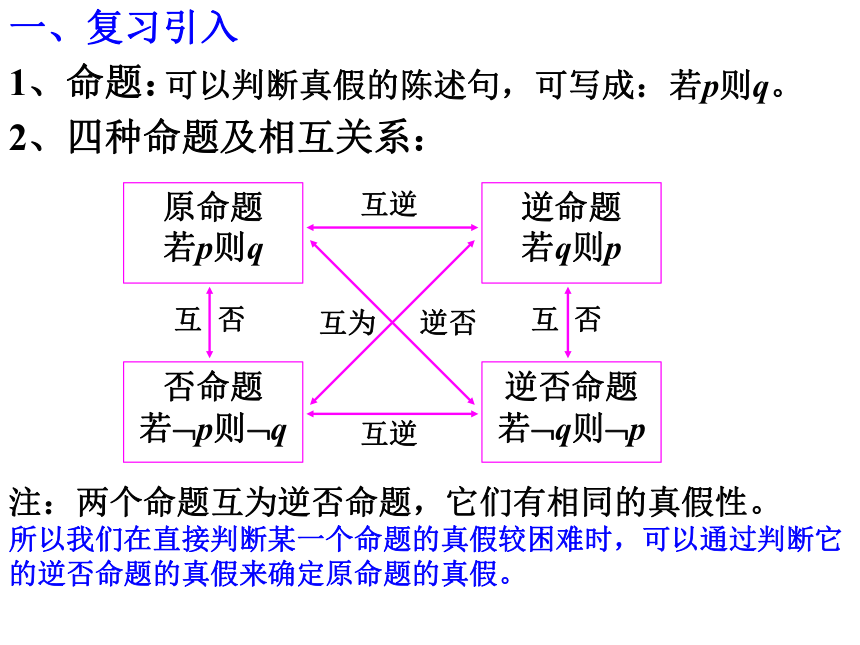
2、四种命题及相互关系:
一、复习引入
注:两个命题互为逆否命题,它们有相同的真假性。
所以我们在直接判断某一个命题的真假较困难时,可以通过判断它的逆否命题的真假来确定原命题的真假。
(2)因为若ab=0 则应该有a=0 或b=0。
所以并不能得到a一定为0。所以是假命题
例 :判断下列命题的真假。
(1)若x>a2+b2,则x>2ab。
(2)若ab=0,则a=0。
解:(1)因为若x>a2+b2,而a2+b2≥2ab,
所以可以得到x>2ab。所以是真命题.
一、复习引入
一般地,“若p,则q”为真命题,是指由p通过推理可以得出q.
这时,我们就说,由p可推出q,
记作:p?q(或q?p)
并且说p是q的充分条件,q是p的必要条件.
命题(1)可记作 x>a2+b2?x>2ab
其中,x>a2+b2是x>2ab的充分条件
x>2ab是x>a2+b2的必要条件
如果“若p,则q”为假命题,那么由p推不出q.
记作:p?q(q?p)
此时,我们就说p不是q的充分条件,q不是p的必要条件.
命题(2)可记作 ab=0?a=0
其中,ab=0不是a=0的充分条件
a=0不是ab=0的必要条件
p?q,则p是q的充分条件,
q是p的必要条件
P
Q
理解充分条件和必要条件
若x>3, 则x>1.
如果已知p?q,则说p是q的充分条件,q是p的必要条件。
简化定义:
例1、下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?
(1)若x=1,则x2 –4x+3=0;
(2)若f(x)=x,则f(x)为增函数;
(3)若x为无理数,则x2为无理数
解:命题(1)(2)是真命题,命题(3)是假命题.
所以命题(1)(2)中的p是q的充分条件
二、新课
例2、下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件?
(1) 若x=y,则x2=y2;
(2) 若两个三角形全等,则这两个三角形的面积相等;
(3) 若a>b,则ac>bc。
解:命题(1)(2)是真命题,命题(3)是假命题,
所以命题(1)(2)中的q是p的必要条件。
二、新课
1、用符号“充分”或“必要”填空:
(1)“0(2)“四边形的对角线相等”是“这个平行四边形为正方形”的_______条件。
(3)“个位数是5的整数”是“这个数能被5整除”的_______条件。
三、能力测试
充分
必要
充分
1.2.2充要条件
思考:已知p:整数a是6的倍数,q:整数a是2和3的倍数.那么p和q是什么关系?
p?q且q?p
1、定义:
称:p是q的充分必要条件,简称充要条件
显然,如果p是q的充要条件,那么q也是p的充要条件
p与q互为充要条件
(也可以说成“p与q等价”“q当且仅当p”)
如果既有p?q,又有q?p就记做p?q
2、各种充分条件、必要条件:
(2)如果A?B且B?A,
那么A是B的充分不必要条件
(3)如果A?B且B?A,
那么A是B的必要不充分条件
(4)如果A?B且B?A,
那么A是B的既不充分也不必要条件
(1)如果A?B且B?A,
那么A是B的充要条件
A
B
A
B
A
B
A=B
B?A
A?B
充分非必要条件
必要非充分条件
既不充分也不必要条件
充分且必要条件
2、从逻辑推理关系看充分条件、必要条件:
1)A?B且B?A,则A是B的
2)若A?B且B?A,则A是B的
3)若A?B且B?A,则A是B的
4)A?B且B?A,则A是B的
注:一般情况下若条件甲为x∈A,条件乙为x∈B
3、从集合与集合的关系看充分条件、必要条件
当且仅当A?B时,甲为乙的充分条件;
当且仅当B?A时,甲为乙的必要条件;
当且仅当A=B时,甲为乙的充要条件.
例3、下列各题中,哪些p是q的充要条件?
(1)p:b=0, q:函数f(x)=ax2+bx+c是偶函数
(2)p:x>0,y>0, q:xy>0
(3)p:a>b, q:a+c>b+c
解:在(1)(3)中,p?q,所以(1)(3)中的p是q的充要条件.在(2)中q?p,所以(2)中的p不是q的充要条件.
1、请用“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”填空:
(1)“(x-2)(x-3)=0”是“x=2”的______条件.
(2)“同位角相等”是“两直线平行”的___条件.
(3)“x=3”是“x2=9”的______条件.
(4)“四边形的对角线相等”是“四边形为平行四边形”的__________条件.
充分不必要
必要不充分
充要
既不充分也不必要
练习
2、在下列电路图中,闭合开关A是灯泡B亮的什么条件:
如图(1)所示,开关A闭合是灯泡B亮的____________条件;
如图(2)所示,开关A闭合是灯泡B亮的____________条件;
如图(3)所示,开关A闭合是灯泡B亮的____________条件;
如图(4)所示,开关A闭合是灯泡B亮的____________条件;
充分不必要
必要不充分
充要
既不充分也不必要
练习、已知条件p:A={x|x2-(a+1)x+a≤0},
条件q:B={x|x2-3x+2≤0},当a为何值时:
(1)p是q的充分不必要条件?
(2)p是q的必要不充分条件?
(3)p是q的充分必要条件?
【解题回顾】充要条件的证明一般分两步:
证充分性即证A ?B,证必要性即证B?A
练习、求证:关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0.
3、在△ABC中,“A>B”是“cosA<cosB”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
C
4、“若p,则q”为真命题,下列说法一定正确的是( )
A.?p是?q的充分条件
B.?p是?q的必要条件
C.?p是?q的充要条件
D.?p是?q的既不充分也不必要条件
B
练习
5、填写“充分不必要,必要不充分,充要,既不充分又不必要”。
(1)sinA>sinB是A>B的_________ 条件。
(2)在△ABC中,sinA>sinB是 A>B的________条件。
既不充分又不必要
充要
6、a>b成立的充分不必要的条件是( )
A. ac>bc B. a/c>b/c
C. a+c>b+c D. ac2>bc2
D
充分不必要
必要不充分
8.方程ax2+bx+c=0(a≠0)有实数根是ac<0的____________条件.
必要不充分
9、已知关于x的方程 (1-a)x2+(a+2)x-4=0(a∈R).
求:(1)方程有两个正根的充要条件;
(2)方程至少有一个正根的充要条件。
【解题回顾】
一是容易漏掉讨论方程二次项系数是否为零,二是只求必要条件忽略验证充分条件.即以所求的必要条件代替充要条件.
1.在判断条件时,要特别注意的是它们能否互相推出,切不可不加判断以单向推出代替双向推出.
注意点
2.弄清楚
①A是B的充分条件与A是B的充分不必要条件之间的区别与联系;
②A是B的必要条件与A是B的必要不充分条件之间的区别与联系
3、注意几种方法的灵活使用:
定义法、集合法、逆否命题法
如果已知p?q,则说p是q的充分条件, q是p的必要条件。
① 认清条件和结论。
② 考察p?q和q?p的真假。
① 可先简化命题。
③ 将命题转化为等价的逆否命题后再判断。
② 否定一个命题只要举出一个反例即可。
1、定义:
2、判别步骤:
3、判别技巧:
四、小结
必要条件
原命题
若p则q
逆否命题
若?q则?p
否命题
若?p则?q
逆命题
若q则p
互逆
互逆
互 否
互 否
互为 逆否
1、命题:
可以判断真假的陈述句,可写成:若p则q。
2、四种命题及相互关系:
一、复习引入
注:两个命题互为逆否命题,它们有相同的真假性。
所以我们在直接判断某一个命题的真假较困难时,可以通过判断它的逆否命题的真假来确定原命题的真假。
(2)因为若ab=0 则应该有a=0 或b=0。
所以并不能得到a一定为0。所以是假命题
例 :判断下列命题的真假。
(1)若x>a2+b2,则x>2ab。
(2)若ab=0,则a=0。
解:(1)因为若x>a2+b2,而a2+b2≥2ab,
所以可以得到x>2ab。所以是真命题.
一、复习引入
一般地,“若p,则q”为真命题,是指由p通过推理可以得出q.
这时,我们就说,由p可推出q,
记作:p?q(或q?p)
并且说p是q的充分条件,q是p的必要条件.
命题(1)可记作 x>a2+b2?x>2ab
其中,x>a2+b2是x>2ab的充分条件
x>2ab是x>a2+b2的必要条件
如果“若p,则q”为假命题,那么由p推不出q.
记作:p?q(q?p)
此时,我们就说p不是q的充分条件,q不是p的必要条件.
命题(2)可记作 ab=0?a=0
其中,ab=0不是a=0的充分条件
a=0不是ab=0的必要条件
p?q,则p是q的充分条件,
q是p的必要条件
P
Q
理解充分条件和必要条件
若x>3, 则x>1.
如果已知p?q,则说p是q的充分条件,q是p的必要条件。
简化定义:
例1、下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?
(1)若x=1,则x2 –4x+3=0;
(2)若f(x)=x,则f(x)为增函数;
(3)若x为无理数,则x2为无理数
解:命题(1)(2)是真命题,命题(3)是假命题.
所以命题(1)(2)中的p是q的充分条件
二、新课
例2、下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件?
(1) 若x=y,则x2=y2;
(2) 若两个三角形全等,则这两个三角形的面积相等;
(3) 若a>b,则ac>bc。
解:命题(1)(2)是真命题,命题(3)是假命题,
所以命题(1)(2)中的q是p的必要条件。
二、新课
1、用符号“充分”或“必要”填空:
(1)“0
(3)“个位数是5的整数”是“这个数能被5整除”的_______条件。
三、能力测试
充分
必要
充分
1.2.2充要条件
思考:已知p:整数a是6的倍数,q:整数a是2和3的倍数.那么p和q是什么关系?
p?q且q?p
1、定义:
称:p是q的充分必要条件,简称充要条件
显然,如果p是q的充要条件,那么q也是p的充要条件
p与q互为充要条件
(也可以说成“p与q等价”“q当且仅当p”)
如果既有p?q,又有q?p就记做p?q
2、各种充分条件、必要条件:
(2)如果A?B且B?A,
那么A是B的充分不必要条件
(3)如果A?B且B?A,
那么A是B的必要不充分条件
(4)如果A?B且B?A,
那么A是B的既不充分也不必要条件
(1)如果A?B且B?A,
那么A是B的充要条件
A
B
A
B
A
B
A=B
B?A
A?B
充分非必要条件
必要非充分条件
既不充分也不必要条件
充分且必要条件
2、从逻辑推理关系看充分条件、必要条件:
1)A?B且B?A,则A是B的
2)若A?B且B?A,则A是B的
3)若A?B且B?A,则A是B的
4)A?B且B?A,则A是B的
注:一般情况下若条件甲为x∈A,条件乙为x∈B
3、从集合与集合的关系看充分条件、必要条件
当且仅当A?B时,甲为乙的充分条件;
当且仅当B?A时,甲为乙的必要条件;
当且仅当A=B时,甲为乙的充要条件.
例3、下列各题中,哪些p是q的充要条件?
(1)p:b=0, q:函数f(x)=ax2+bx+c是偶函数
(2)p:x>0,y>0, q:xy>0
(3)p:a>b, q:a+c>b+c
解:在(1)(3)中,p?q,所以(1)(3)中的p是q的充要条件.在(2)中q?p,所以(2)中的p不是q的充要条件.
1、请用“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”填空:
(1)“(x-2)(x-3)=0”是“x=2”的______条件.
(2)“同位角相等”是“两直线平行”的___条件.
(3)“x=3”是“x2=9”的______条件.
(4)“四边形的对角线相等”是“四边形为平行四边形”的__________条件.
充分不必要
必要不充分
充要
既不充分也不必要
练习
2、在下列电路图中,闭合开关A是灯泡B亮的什么条件:
如图(1)所示,开关A闭合是灯泡B亮的____________条件;
如图(2)所示,开关A闭合是灯泡B亮的____________条件;
如图(3)所示,开关A闭合是灯泡B亮的____________条件;
如图(4)所示,开关A闭合是灯泡B亮的____________条件;
充分不必要
必要不充分
充要
既不充分也不必要
练习、已知条件p:A={x|x2-(a+1)x+a≤0},
条件q:B={x|x2-3x+2≤0},当a为何值时:
(1)p是q的充分不必要条件?
(2)p是q的必要不充分条件?
(3)p是q的充分必要条件?
【解题回顾】充要条件的证明一般分两步:
证充分性即证A ?B,证必要性即证B?A
练习、求证:关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0.
3、在△ABC中,“A>B”是“cosA<cosB”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
C
4、“若p,则q”为真命题,下列说法一定正确的是( )
A.?p是?q的充分条件
B.?p是?q的必要条件
C.?p是?q的充要条件
D.?p是?q的既不充分也不必要条件
B
练习
5、填写“充分不必要,必要不充分,充要,既不充分又不必要”。
(1)sinA>sinB是A>B的_________ 条件。
(2)在△ABC中,sinA>sinB是 A>B的________条件。
既不充分又不必要
充要
6、a>b成立的充分不必要的条件是( )
A. ac>bc B. a/c>b/c
C. a+c>b+c D. ac2>bc2
D
充分不必要
必要不充分
8.方程ax2+bx+c=0(a≠0)有实数根是ac<0的____________条件.
必要不充分
9、已知关于x的方程 (1-a)x2+(a+2)x-4=0(a∈R).
求:(1)方程有两个正根的充要条件;
(2)方程至少有一个正根的充要条件。
【解题回顾】
一是容易漏掉讨论方程二次项系数是否为零,二是只求必要条件忽略验证充分条件.即以所求的必要条件代替充要条件.
1.在判断条件时,要特别注意的是它们能否互相推出,切不可不加判断以单向推出代替双向推出.
注意点
2.弄清楚
①A是B的充分条件与A是B的充分不必要条件之间的区别与联系;
②A是B的必要条件与A是B的必要不充分条件之间的区别与联系
3、注意几种方法的灵活使用:
定义法、集合法、逆否命题法
如果已知p?q,则说p是q的充分条件, q是p的必要条件。
① 认清条件和结论。
② 考察p?q和q?p的真假。
① 可先简化命题。
③ 将命题转化为等价的逆否命题后再判断。
② 否定一个命题只要举出一个反例即可。
1、定义:
2、判别步骤:
3、判别技巧:
四、小结
