1.4简单的逻辑连接词-北师大版高中数学选修2-1课件(21张PPT)
文档属性
| 名称 | 1.4简单的逻辑连接词-北师大版高中数学选修2-1课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 699.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:36:22 | ||
图片预览







文档简介
1.4简单的逻辑联结词
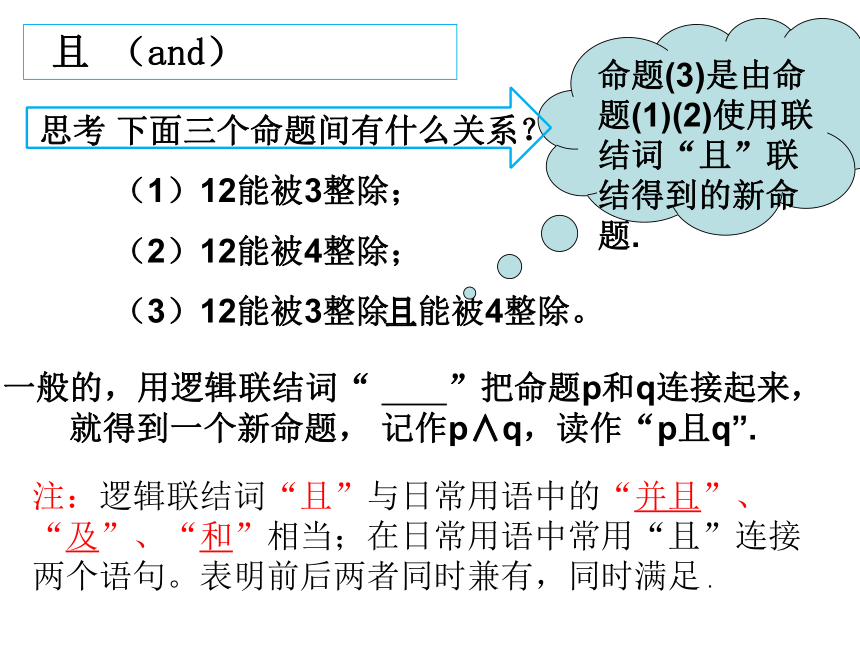
一般的,用逻辑联结词“ ”把命题p和q连接起来,就得到一个新命题, 记作p∧q,读作“p且q”.
思考 下面三个命题间有什么关系?
(1)12能被3整除;
(2)12能被4整除;
(3)12能被3整除 能被4整除。
且
且
注:逻辑联结词“且”与日常用语中的“并且”、“及”、“和”相当;在日常用语中常用“且”连接两个语句。表明前后两者同时兼有,同时满足 .
且 (and)
命题(3)是由命题(1)(2)使用联结词“且”联结得到的新命题.
例1、将下列命题用“且”联结成新命题,并判断它们的真假:
(1)p:平行四边形的对角线互相平分,q:平行四边形的对角线相等.
p∧q:平行四边形的对角线互相平分且相等.由于p是真命题,q是假命题,所以p∧q是假命题
(2)p:菱形的对角线互相垂直,q:菱形的对角线互相平分.
p∧q:菱形的对角线互相垂直且平分.由于p是真命题,q是真命题,所以p∧q是真命题
(3)p:35是15的倍数,q:35是7的倍数
p∧q:35是15的倍数且是7的倍数.由于p是假命题,q是真命题,所以p∧q是假命题
一、由“且”构成的复合命题
定义:一般地,用联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作 p∧q,读作“p且q”
思考:命题 p∧q的真假如何确定?
注:对“且”的理解,可联想集合中的“交集”的概念。 中的“且”,它是指x∈A,x∈B都满足的意思。即x既属于集合A,同时又属于集合B。
x| x∈A且x ∈B
A∩B=
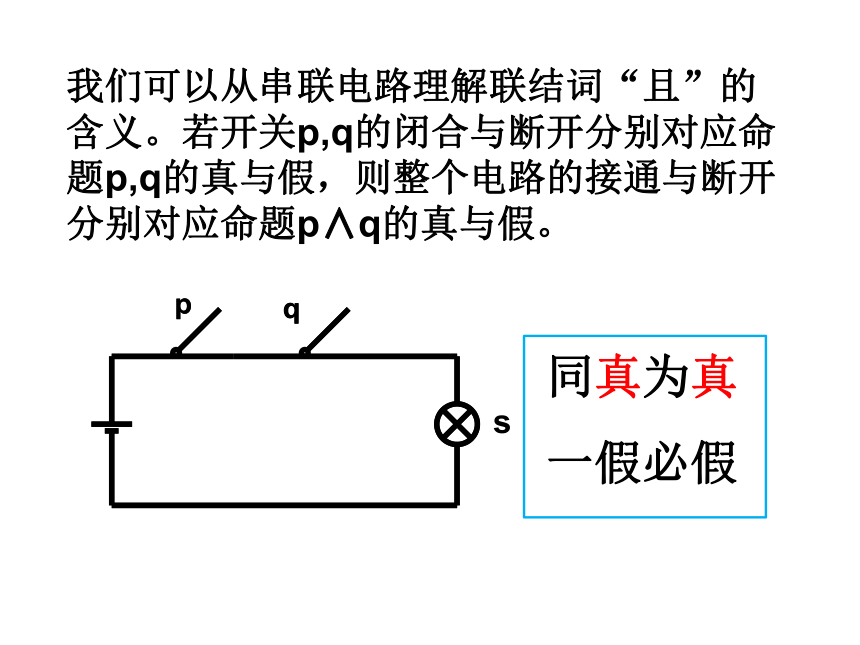
我们可以从串联电路理解联结词“且”的含义。若开关p,q的闭合与断开分别对应命题p,q的真与假,则整个电路的接通与断开分别对应命题p∧q的真与假。
p
q
s
p
q
同真为真
一假必假
思考 下列三个命题间有什么关系?
(1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数 是9的倍数。
或
或
一般地,用逻辑联结词“ ”把命题p和命题q联结起来,
就得到一个新命题,记作p∨q, 读作“p或q”
注:日常生活中的“或”有两类用法:其一是“不可兼有”的“或”;其二是“可兼有”的“或”。逻辑连接词中的“或”为日常生活中 “可兼有”的“或”。
或 (or)
命题(3)是由命题(1)(2)使用联结词“或”联结得到的新命题.
练习
1、判断下列命题的真假:
(1)12是48且是36的约数;
(2)矩形的对角线互相垂直且平分。
真
假
2、用逻辑联结词“且”改写下列命题,并判断真假。
(1)y=cosx是周期函数,又是偶函数;
(2)24是8的倍数,又是9的倍数.
真
假
一般地,我们规定:当p,q两个命题中
有 个命题是真命题时,p∨q是 命题;
当p,q两个命题都是假命题时,p∨q
是 命题.
一句话概括:
同假为假,一真必真.
一
真
假
命题p∨q的真假判断方法:
p
q
p∨q
真
真
真
假
假
真
假
假
假
真
真
真
一般地,我们规定:
当p,q都是真命题时,p∧q是真命题;当p,q 两个命题中有一个命题是假命题时,p∧q是假命题。
全真为真,有假即假.
p
q
我们可以从串联电路理解联结词“且”的含义。若开关p,q的闭合与断开分别对应命题p,q的真与假,则整个电路的接通与断开分别对应命题p∧q的真假。
例3:判断下列命题的真假:
(1)2≤2;
(2)集合A是A∩B的子集或是A∪B的子集;
(3)周长相等的两个三角形全等或面积相等的两个三角形全等.
解:(1)p:2=2 ;q:2<2
∵ p是真命题,∴p∨q是真命题.
(3)p:周长相等的两个三角形全等;
q:面积相等的两个三角形全等.
∵命题p、q都是假命题, ∴ p∨q是假命题.
(2)p:集合A是A∩B的子集;q:集合A是A∪B的子集
∵q是真命题, ∴p∨q是真命题.
例题分析
例3:判断下列命题的真假:
(1)2≤2;
(2)集合A是A∩B的子集或是A∪B的子集;
(3)周长相等的两个三角形全等或面积相等的两个三角形全等。
解:(1)命题“2≤2”是由命题:p:2=2;q:2<2
用“或”联结后构成的新命题,即p ∨ q.
因为命题p是真命题,所以命题p ∨ q是真命题。
解:(2)命题“集合A是A∩B的子集或是A∪B的子集”是由命题:
p:集合A是A∩B的子集;q:集合A是A∪B的子集
用“或”联结后构成的新命题,即p ∨ q.
因为命题q是真命题,所以命题p ∨ q是真命题。
解:(3)命题“周长相等的两个三角形全等或面积相等的两个三角形全等”是由命题:
p:周长相等的两个三角形全等;
q:面积相等的两个三角形全等
用“或”联结后构成的新命题,即p ∨ q.
因为命题p,q都是假命题,所以命题p ∨ q是假命题。
思考: 下面两个命题间有什么关系?
(1)、35能被5整除;
(2) 、 35 能被5整除。
一般地,对一个命题p ,就能得到一个新命题,
记作 p,读作“非p”或“p的否定”
不
不
全盘否定
若p是真命题,则 p必是假命题;若p是假命题,则 p必是真命题。真假相反
非 (not)
例5 写出下列命题的否定,并判断它们的真假:
(1)p:y=sinx 是周期函数;
(2)p:3 < 2
(3) p:空集是集合A的子集
p
解: : y=sinx不是周期函数。
p
解: : 3≥2.
p
解: : 空集不是集合A的子集。
假
假
真
练习
5、写出下列命题的否定
(1)p:我们班的同学都是团员
(2)p:我们班至少有10名团员
(3)p:我们班至多有10名团员
(4)p:奇数是质数
?p:我们班的同学不都是团员
?p: 我们班至多有9名团员
?p: 我们班至少有11名团员
?p: 有些奇数不是质数
p
q
非p
p且q
p或q
真
真
假
真
真
真
假
假
假
真
假
真
真
假
真
假
假
真
假
假
真值表:
非p
真假相反
p且q
一假必假
p或q
一真必真
张三说:“是李四做的”;
李四说:“不是我做的”;
王二说:“不是我做的”。
战三说
的是真话
李四说
的是假话
王二说
的是假话
是我做的
是我做的
是李四做的
矛盾!
小结:
1、体会数学中“且”“或”的意义,并注意与实际生活中的语言相区别;
2、会判断命题“p且q”“p或q”的真假。
1.命题“方程 的解是 ”中,使用逻辑词的情况是( )
A.没有使用逻辑联结词
B.使用了逻辑联结词“或”
C. 使用了逻辑联结词“且”
D. 使用了逻辑联结词“或”与“且”
B
练习
2.在下列命题中
(1)命题“不等式 没有实数解”;
(2)命题“-1是偶数或奇数”;
(3)命题“ 既属于集合 ,也属于集合 ”;
(4)命题“ ”
其中,真命题为_____________.
(2)(4)
“或”:不等式 x2?x?6>0的解集{ x | x3 }
“且”:不等式 x2?x?6<0的解集 { x | ?2< x<3 }
即 { x | x>?2且x<3 }
“非”:三角形的内角和不大于180°
“或” A∪B={x|x∈A或x∈B}
“且” A∩B={x|x∈A且x∈B}
“非” ?UA={x|x∈U且x?A}
“或”、“且”、“非”与集合的意义相同吗?
拓展延伸
一般的,用逻辑联结词“ ”把命题p和q连接起来,就得到一个新命题, 记作p∧q,读作“p且q”.
思考 下面三个命题间有什么关系?
(1)12能被3整除;
(2)12能被4整除;
(3)12能被3整除 能被4整除。
且
且
注:逻辑联结词“且”与日常用语中的“并且”、“及”、“和”相当;在日常用语中常用“且”连接两个语句。表明前后两者同时兼有,同时满足 .
且 (and)
命题(3)是由命题(1)(2)使用联结词“且”联结得到的新命题.
例1、将下列命题用“且”联结成新命题,并判断它们的真假:
(1)p:平行四边形的对角线互相平分,q:平行四边形的对角线相等.
p∧q:平行四边形的对角线互相平分且相等.由于p是真命题,q是假命题,所以p∧q是假命题
(2)p:菱形的对角线互相垂直,q:菱形的对角线互相平分.
p∧q:菱形的对角线互相垂直且平分.由于p是真命题,q是真命题,所以p∧q是真命题
(3)p:35是15的倍数,q:35是7的倍数
p∧q:35是15的倍数且是7的倍数.由于p是假命题,q是真命题,所以p∧q是假命题
一、由“且”构成的复合命题
定义:一般地,用联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作 p∧q,读作“p且q”
思考:命题 p∧q的真假如何确定?
注:对“且”的理解,可联想集合中的“交集”的概念。 中的“且”,它是指x∈A,x∈B都满足的意思。即x既属于集合A,同时又属于集合B。
x| x∈A且x ∈B
A∩B=
我们可以从串联电路理解联结词“且”的含义。若开关p,q的闭合与断开分别对应命题p,q的真与假,则整个电路的接通与断开分别对应命题p∧q的真与假。
p
q
s
p
q
同真为真
一假必假
思考 下列三个命题间有什么关系?
(1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数 是9的倍数。
或
或
一般地,用逻辑联结词“ ”把命题p和命题q联结起来,
就得到一个新命题,记作p∨q, 读作“p或q”
注:日常生活中的“或”有两类用法:其一是“不可兼有”的“或”;其二是“可兼有”的“或”。逻辑连接词中的“或”为日常生活中 “可兼有”的“或”。
或 (or)
命题(3)是由命题(1)(2)使用联结词“或”联结得到的新命题.
练习
1、判断下列命题的真假:
(1)12是48且是36的约数;
(2)矩形的对角线互相垂直且平分。
真
假
2、用逻辑联结词“且”改写下列命题,并判断真假。
(1)y=cosx是周期函数,又是偶函数;
(2)24是8的倍数,又是9的倍数.
真
假
一般地,我们规定:当p,q两个命题中
有 个命题是真命题时,p∨q是 命题;
当p,q两个命题都是假命题时,p∨q
是 命题.
一句话概括:
同假为假,一真必真.
一
真
假
命题p∨q的真假判断方法:
p
q
p∨q
真
真
真
假
假
真
假
假
假
真
真
真
一般地,我们规定:
当p,q都是真命题时,p∧q是真命题;当p,q 两个命题中有一个命题是假命题时,p∧q是假命题。
全真为真,有假即假.
p
q
我们可以从串联电路理解联结词“且”的含义。若开关p,q的闭合与断开分别对应命题p,q的真与假,则整个电路的接通与断开分别对应命题p∧q的真假。
例3:判断下列命题的真假:
(1)2≤2;
(2)集合A是A∩B的子集或是A∪B的子集;
(3)周长相等的两个三角形全等或面积相等的两个三角形全等.
解:(1)p:2=2 ;q:2<2
∵ p是真命题,∴p∨q是真命题.
(3)p:周长相等的两个三角形全等;
q:面积相等的两个三角形全等.
∵命题p、q都是假命题, ∴ p∨q是假命题.
(2)p:集合A是A∩B的子集;q:集合A是A∪B的子集
∵q是真命题, ∴p∨q是真命题.
例题分析
例3:判断下列命题的真假:
(1)2≤2;
(2)集合A是A∩B的子集或是A∪B的子集;
(3)周长相等的两个三角形全等或面积相等的两个三角形全等。
解:(1)命题“2≤2”是由命题:p:2=2;q:2<2
用“或”联结后构成的新命题,即p ∨ q.
因为命题p是真命题,所以命题p ∨ q是真命题。
解:(2)命题“集合A是A∩B的子集或是A∪B的子集”是由命题:
p:集合A是A∩B的子集;q:集合A是A∪B的子集
用“或”联结后构成的新命题,即p ∨ q.
因为命题q是真命题,所以命题p ∨ q是真命题。
解:(3)命题“周长相等的两个三角形全等或面积相等的两个三角形全等”是由命题:
p:周长相等的两个三角形全等;
q:面积相等的两个三角形全等
用“或”联结后构成的新命题,即p ∨ q.
因为命题p,q都是假命题,所以命题p ∨ q是假命题。
思考: 下面两个命题间有什么关系?
(1)、35能被5整除;
(2) 、 35 能被5整除。
一般地,对一个命题p ,就能得到一个新命题,
记作 p,读作“非p”或“p的否定”
不
不
全盘否定
若p是真命题,则 p必是假命题;若p是假命题,则 p必是真命题。真假相反
非 (not)
例5 写出下列命题的否定,并判断它们的真假:
(1)p:y=sinx 是周期函数;
(2)p:3 < 2
(3) p:空集是集合A的子集
p
解: : y=sinx不是周期函数。
p
解: : 3≥2.
p
解: : 空集不是集合A的子集。
假
假
真
练习
5、写出下列命题的否定
(1)p:我们班的同学都是团员
(2)p:我们班至少有10名团员
(3)p:我们班至多有10名团员
(4)p:奇数是质数
?p:我们班的同学不都是团员
?p: 我们班至多有9名团员
?p: 我们班至少有11名团员
?p: 有些奇数不是质数
p
q
非p
p且q
p或q
真
真
假
真
真
真
假
假
假
真
假
真
真
假
真
假
假
真
假
假
真值表:
非p
真假相反
p且q
一假必假
p或q
一真必真
张三说:“是李四做的”;
李四说:“不是我做的”;
王二说:“不是我做的”。
战三说
的是真话
李四说
的是假话
王二说
的是假话
是我做的
是我做的
是李四做的
矛盾!
小结:
1、体会数学中“且”“或”的意义,并注意与实际生活中的语言相区别;
2、会判断命题“p且q”“p或q”的真假。
1.命题“方程 的解是 ”中,使用逻辑词的情况是( )
A.没有使用逻辑联结词
B.使用了逻辑联结词“或”
C. 使用了逻辑联结词“且”
D. 使用了逻辑联结词“或”与“且”
B
练习
2.在下列命题中
(1)命题“不等式 没有实数解”;
(2)命题“-1是偶数或奇数”;
(3)命题“ 既属于集合 ,也属于集合 ”;
(4)命题“ ”
其中,真命题为_____________.
(2)(4)
“或”:不等式 x2?x?6>0的解集{ x | x3 }
“且”:不等式 x2?x?6<0的解集 { x | ?2< x<3 }
即 { x | x>?2且x<3 }
“非”:三角形的内角和不大于180°
“或” A∪B={x|x∈A或x∈B}
“且” A∩B={x|x∈A且x∈B}
“非” ?UA={x|x∈U且x?A}
“或”、“且”、“非”与集合的意义相同吗?
拓展延伸
