2020-2021学年湘教新版八年级上册数学期末复习试卷1(含解析)
文档属性
| 名称 | 2020-2021学年湘教新版八年级上册数学期末复习试卷1(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 137.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 00:00:00 | ||
图片预览



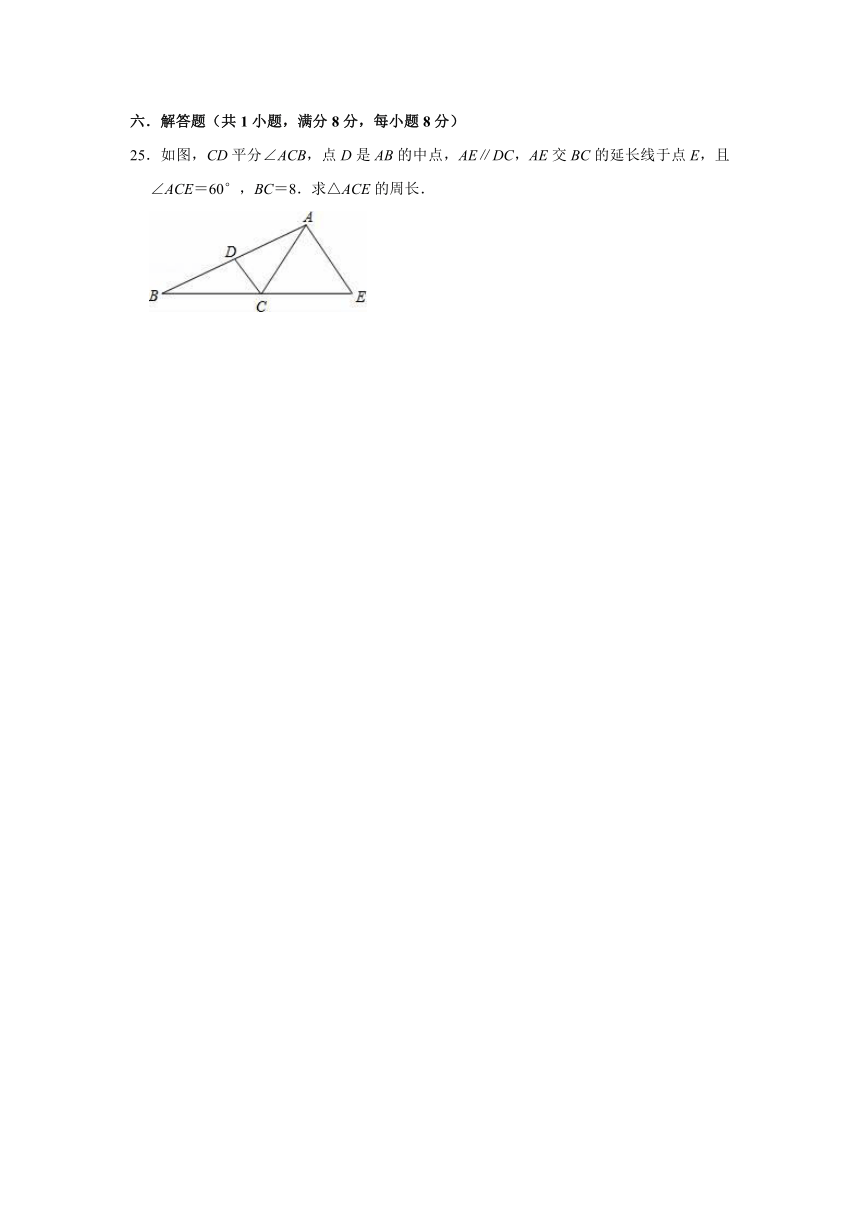

文档简介
2020-2021学年湘教新版八年级上册数学期末复习试卷1
一.选择题(共10小题,满分30分,每小题3分)
1.下列代数式中,分式有( )个.
,,,﹣,,,
+3,
A.5
B.4
C.3
D.2
2.计算()2的结果是( )
A.﹣2
B.2
C.±2
D.4
3.分式有意义的条件是( )
A.x≠0
B.y≠0
C.x≠3
D.x≠﹣3
4.不等式x﹣2>2x﹣4的解集在数轴上表示为( )
A.
B.
C.
D.
5.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.3cm,4cm,8cm
B.8cm,7cm,15cm
C.13cm,12cm,20cm
D.5cm,5cm,11cm
6.如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )
A.BC=BE
B.AC=DE
C.∠A=∠D
D.∠ACB=∠DEB
7.设a、b、c均为正数,若,则a、b、c三个数的大小关系是( )
A.c<a<b
B.b<c<a
C.a<b<c
D.c<b<a
8.如图,在△ABC中,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,分别交AB、AC于点E、F,当∠A大小变化时,线段EF和BE+CF的大小关系是( )
A.EF>BE+CF
B.EF<BE+CF
C.EF=BE+CF
D.不能确定
9.已知0≤a﹣b≤1且1≤a+b≤4,则a的取值范围是( )
A.1≤a≤2
B.2≤a≤3
C.≤a≤
D.≤a≤
10.一同学将方程x2﹣4x﹣3=0化成了(x+m)2=n的形式,则m、n的值应为( )
A.m=﹣2,n=7
B.m=2.n=7
C.m=﹣2,n=1
D.m=2.n=﹣7
二.填空题(共8小题,满分24分,每小题3分)
11.的平方根是
.
12.式子中x的取值范围是
.
13.某次知识竞赛共有20道题,每答对一题得10分,答错或不答都扣5分,娜娜得分要不低于80分,设她答对了x道题,则根据题意可列不等式为
.
14.计算:(2+)(2﹣)=
.
15.把命题“同位角相等”改写成“如果…那么…”的形式为
.
16.如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的底角度数是
.
17.若分式方程要产生增根,则a=
.
18.如图是一组有规律的图案,第1个图案由6个基础图形组成,第2个图案由11个基础图形组成,…,第n(n是正整数)个图案中由
个基础图形组成.(用含n的代数式表示)
三.解答题(共4小题,满分24分,每小题6分)
19.计算:|﹣3|﹣(﹣π)0+()﹣1+(﹣1)2019﹣.
20.解分式方程:.
21.求满足不等式组的所有整数解.
22.先化简,再求值(1﹣)÷,其中x=+1.
四.解答题(共1小题,满分7分,每小题7分)
23.如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从点B向点C运动,点E同时从C出发以每秒2个单位的速度在线段CA上向点A运动,连接AD、DE,设D、E两点运动时间为t秒(0<t<4)
(1)运动
秒时,AE=DC;
(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;
(3)若△ABD≌△DCE,∠BAC=α,则∠ADE=
(用含α的式子表示).
五.解答题(共1小题,满分7分,每小题7分)
24.某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成:若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲乙两队合作完成该工程需要多少天?
六.解答题(共1小题,满分8分,每小题8分)
25.如图,CD平分∠ACB,点D是AB的中点,AE∥DC,AE交BC的延长线于点E,且∠ACE=60°,BC=8.求△ACE的周长.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:分式有:,,﹣,,共4个,
故选:B.
2.解:()2=2,
故选:B.
3.解:根据分式有意义的条件,得x﹣3≠0
解得x≠3.
故选:C.
4.解:x﹣2>2x﹣4,
x﹣2x>﹣4+2,
﹣x>﹣2,
x<2.
将不等式的解集表示在数轴上为:.
故选:D.
5.解:A、3+4<8,不能组成三角形;
B、8+7=15,不能组成三角形;
C、13+12>20,能够组成三角形;
D、5+5<11,不能组成三角形.
故选:C.
6.解:A、添加BC=BE,可根据SAS判定△ABC≌△DBE,故正确;
B、添加AC=DE,SSA不能判定△ABC≌△DBE,故错误;
C、添加∠A=∠D,可根据ASA判定△ABC≌△DBE,故正确;
D、添加∠ACB=∠DEB,可根据AAS判定△ABC≌△DBE,故正确.
故选:B.
7.解:∵a、b、c均为正数,根据,
则,
上式同时加1得:,
化简得:,
∴c<a<b.
故选:A.
8.解:∵EF∥BC,
∴∠EDB=∠DBC,
∵BD平分∠ABC,
∴∠EBD=∠DBC,
∴∠EDB=∠EBD,
∴ED=BE,
同理DF=FC,
∴ED+DF=BE+FC,
即EF=BE+CF,
故选:C.
9.解:0≤a﹣b≤1①,
1≤a+b≤4②,
①+②得1≤2a≤5,
0.5≤a≤2.5,
故选:C.
10.解:∵(x+m)2=n可化为:x2+2mx+m2﹣n=0,
∴,解得:.
故选:A.
二.填空题(共8小题,满分24分,每小题3分)
11.解:=10,
10的平方根是.
故答案为:±.
12.解:根据题意得,x+2≥0且x﹣1≠0,
解得x≥﹣2且x≠1.
故答案为:x≥﹣2且x≠1.
13.解:设她答对了x道题,则答错或不答的有(20﹣x)道,
由题意得:10x﹣5(20﹣x)≥80,
故答案为:10x﹣5(20﹣x)≥80.
14.解:原式=22﹣()2
=4﹣3
=1.
15.解:命题“同位角相等”改写成“如果…那么…”的形式为:如果两个角是同位角,那么这两个角相等.
故答案为如果两个角是同位角,那么这两个角相等.
16.解:∵在△CBA1中,∠B=30°,A1B=CB,
∴∠BA1C==75°,
∵A1A2=A1D,∠BA1C是△A1A2D的外角,
∴∠DA2A1=∠BA1C=×75°;
同理可得∠EA3A2=()2×75°,∠FA4A3=()3×75°,
∴第n个三角形中以An为顶点的内角度数是()
n﹣1×75°.
故答案为:()
n﹣1×75°.
17.解:去分母得:x+1=a,
由分式方程有增根,得到x=1或x=﹣1,
当x=1时,a=2;当x=﹣1时,a=0,
综上,a=2或0.
故答案为:2或0.
18.解:第1个图案由6个基础图形组成,
第2个图案由11个基础图形组成,11=5×2+1,
第3个图案由16个基础图形组成,16=5×3+1,
…,
第n个图案由5n+1个基础图形组成.
故答案为:5n+1.
三.解答题(共4小题,满分24分,每小题6分)
19.解:原式=3﹣1+4﹣1﹣3=2.
20.解:去分母得:(x+2)2﹣16=x﹣2,
整理得:x2+3x﹣10=0,即(x﹣2)(x+5)=0,
解得:x=2或x=﹣5,
经检验x=2是增根,分式方程的解为x=﹣5.
21.解:解不等式x﹣3(x﹣2)≤8,得:x≥﹣1,
解不等式x﹣1<3﹣x,得:x<2,
则不等式组的解集为﹣1≤x<2,
所以不等式组的整数解为﹣1、0、1.
22.解:(1﹣)÷
=
=
=,
当x=+1时,原式==.
四.解答题(共1小题,满分7分,每小题7分)
23.解:(1)由题可得,BD=CE=2t,
∴CD=12﹣2t,AE=8﹣2t,
∴当AE=DC,时,8﹣2t=(12﹣2t),
解得t=3,
故答案为:3;
(2)当△ABD≌△DCE成立时,AB=CD=8,
∴12﹣2t=8,
解得t=2,
∴运动2秒时,△ABD≌△DCE能成立;
(3)当△ABD≌△DCE时,∠CDE=∠BAD,
又∵∠ADE=180°﹣∠CDE﹣∠ADB,∠B=∠180°﹣∠BAD﹣∠ADB,
∴∠ADE=∠B,
又∵∠BAC=α,AB=AC,
∴∠ADE=∠B=(180°﹣α)=90°﹣α.
故答案为:90°﹣α.
五.解答题(共1小题,满分7分,每小题7分)
24.解:(1)设这项工程的规定时间是x天,则甲队单独施工需要x天完工,乙队单独施工需要1.5x天完工,
依题意,得:
+=1,
解得:x=30,
经检验,x=30是原方程的解,且符合题意.
答:这项工程的规定时间是30天.
(2)由(1)可知:甲队单独施工需要30天完工,乙队单独施工需要45天完工,
1÷(+)=18(天).
答:甲乙两队合作完成该工程需要18天.
六.解答题(共1小题,满分8分,每小题8分)
25.解:作DE⊥AC于E,DF⊥BC于F.
∵CD平分∠ACB,
∴DE=DF,
∵点D是AB的中点,
∵DB=DA,
∴Rt△DBF≌△Rt△DAE(HL),
∴∠DBF=∠DAE,
∴CA=CB,
∴△ABC是等腰三角形,AC=BC=8,
又∵∠ACE=60°,
∴∠ACB=120°,
又CD平分∠ACB,
∴∠BCD=60°,
∵AE∥DC,
∴∠AEC=∠BCD=60°,
∴△ACE是等边三角形,
∴△ACE的周长为24.
一.选择题(共10小题,满分30分,每小题3分)
1.下列代数式中,分式有( )个.
,,,﹣,,,
+3,
A.5
B.4
C.3
D.2
2.计算()2的结果是( )
A.﹣2
B.2
C.±2
D.4
3.分式有意义的条件是( )
A.x≠0
B.y≠0
C.x≠3
D.x≠﹣3
4.不等式x﹣2>2x﹣4的解集在数轴上表示为( )
A.
B.
C.
D.
5.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.3cm,4cm,8cm
B.8cm,7cm,15cm
C.13cm,12cm,20cm
D.5cm,5cm,11cm
6.如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )
A.BC=BE
B.AC=DE
C.∠A=∠D
D.∠ACB=∠DEB
7.设a、b、c均为正数,若,则a、b、c三个数的大小关系是( )
A.c<a<b
B.b<c<a
C.a<b<c
D.c<b<a
8.如图,在△ABC中,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,分别交AB、AC于点E、F,当∠A大小变化时,线段EF和BE+CF的大小关系是( )
A.EF>BE+CF
B.EF<BE+CF
C.EF=BE+CF
D.不能确定
9.已知0≤a﹣b≤1且1≤a+b≤4,则a的取值范围是( )
A.1≤a≤2
B.2≤a≤3
C.≤a≤
D.≤a≤
10.一同学将方程x2﹣4x﹣3=0化成了(x+m)2=n的形式,则m、n的值应为( )
A.m=﹣2,n=7
B.m=2.n=7
C.m=﹣2,n=1
D.m=2.n=﹣7
二.填空题(共8小题,满分24分,每小题3分)
11.的平方根是
.
12.式子中x的取值范围是
.
13.某次知识竞赛共有20道题,每答对一题得10分,答错或不答都扣5分,娜娜得分要不低于80分,设她答对了x道题,则根据题意可列不等式为
.
14.计算:(2+)(2﹣)=
.
15.把命题“同位角相等”改写成“如果…那么…”的形式为
.
16.如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的底角度数是
.
17.若分式方程要产生增根,则a=
.
18.如图是一组有规律的图案,第1个图案由6个基础图形组成,第2个图案由11个基础图形组成,…,第n(n是正整数)个图案中由
个基础图形组成.(用含n的代数式表示)
三.解答题(共4小题,满分24分,每小题6分)
19.计算:|﹣3|﹣(﹣π)0+()﹣1+(﹣1)2019﹣.
20.解分式方程:.
21.求满足不等式组的所有整数解.
22.先化简,再求值(1﹣)÷,其中x=+1.
四.解答题(共1小题,满分7分,每小题7分)
23.如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从点B向点C运动,点E同时从C出发以每秒2个单位的速度在线段CA上向点A运动,连接AD、DE,设D、E两点运动时间为t秒(0<t<4)
(1)运动
秒时,AE=DC;
(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;
(3)若△ABD≌△DCE,∠BAC=α,则∠ADE=
(用含α的式子表示).
五.解答题(共1小题,满分7分,每小题7分)
24.某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成:若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲乙两队合作完成该工程需要多少天?
六.解答题(共1小题,满分8分,每小题8分)
25.如图,CD平分∠ACB,点D是AB的中点,AE∥DC,AE交BC的延长线于点E,且∠ACE=60°,BC=8.求△ACE的周长.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:分式有:,,﹣,,共4个,
故选:B.
2.解:()2=2,
故选:B.
3.解:根据分式有意义的条件,得x﹣3≠0
解得x≠3.
故选:C.
4.解:x﹣2>2x﹣4,
x﹣2x>﹣4+2,
﹣x>﹣2,
x<2.
将不等式的解集表示在数轴上为:.
故选:D.
5.解:A、3+4<8,不能组成三角形;
B、8+7=15,不能组成三角形;
C、13+12>20,能够组成三角形;
D、5+5<11,不能组成三角形.
故选:C.
6.解:A、添加BC=BE,可根据SAS判定△ABC≌△DBE,故正确;
B、添加AC=DE,SSA不能判定△ABC≌△DBE,故错误;
C、添加∠A=∠D,可根据ASA判定△ABC≌△DBE,故正确;
D、添加∠ACB=∠DEB,可根据AAS判定△ABC≌△DBE,故正确.
故选:B.
7.解:∵a、b、c均为正数,根据,
则,
上式同时加1得:,
化简得:,
∴c<a<b.
故选:A.
8.解:∵EF∥BC,
∴∠EDB=∠DBC,
∵BD平分∠ABC,
∴∠EBD=∠DBC,
∴∠EDB=∠EBD,
∴ED=BE,
同理DF=FC,
∴ED+DF=BE+FC,
即EF=BE+CF,
故选:C.
9.解:0≤a﹣b≤1①,
1≤a+b≤4②,
①+②得1≤2a≤5,
0.5≤a≤2.5,
故选:C.
10.解:∵(x+m)2=n可化为:x2+2mx+m2﹣n=0,
∴,解得:.
故选:A.
二.填空题(共8小题,满分24分,每小题3分)
11.解:=10,
10的平方根是.
故答案为:±.
12.解:根据题意得,x+2≥0且x﹣1≠0,
解得x≥﹣2且x≠1.
故答案为:x≥﹣2且x≠1.
13.解:设她答对了x道题,则答错或不答的有(20﹣x)道,
由题意得:10x﹣5(20﹣x)≥80,
故答案为:10x﹣5(20﹣x)≥80.
14.解:原式=22﹣()2
=4﹣3
=1.
15.解:命题“同位角相等”改写成“如果…那么…”的形式为:如果两个角是同位角,那么这两个角相等.
故答案为如果两个角是同位角,那么这两个角相等.
16.解:∵在△CBA1中,∠B=30°,A1B=CB,
∴∠BA1C==75°,
∵A1A2=A1D,∠BA1C是△A1A2D的外角,
∴∠DA2A1=∠BA1C=×75°;
同理可得∠EA3A2=()2×75°,∠FA4A3=()3×75°,
∴第n个三角形中以An为顶点的内角度数是()
n﹣1×75°.
故答案为:()
n﹣1×75°.
17.解:去分母得:x+1=a,
由分式方程有增根,得到x=1或x=﹣1,
当x=1时,a=2;当x=﹣1时,a=0,
综上,a=2或0.
故答案为:2或0.
18.解:第1个图案由6个基础图形组成,
第2个图案由11个基础图形组成,11=5×2+1,
第3个图案由16个基础图形组成,16=5×3+1,
…,
第n个图案由5n+1个基础图形组成.
故答案为:5n+1.
三.解答题(共4小题,满分24分,每小题6分)
19.解:原式=3﹣1+4﹣1﹣3=2.
20.解:去分母得:(x+2)2﹣16=x﹣2,
整理得:x2+3x﹣10=0,即(x﹣2)(x+5)=0,
解得:x=2或x=﹣5,
经检验x=2是增根,分式方程的解为x=﹣5.
21.解:解不等式x﹣3(x﹣2)≤8,得:x≥﹣1,
解不等式x﹣1<3﹣x,得:x<2,
则不等式组的解集为﹣1≤x<2,
所以不等式组的整数解为﹣1、0、1.
22.解:(1﹣)÷
=
=
=,
当x=+1时,原式==.
四.解答题(共1小题,满分7分,每小题7分)
23.解:(1)由题可得,BD=CE=2t,
∴CD=12﹣2t,AE=8﹣2t,
∴当AE=DC,时,8﹣2t=(12﹣2t),
解得t=3,
故答案为:3;
(2)当△ABD≌△DCE成立时,AB=CD=8,
∴12﹣2t=8,
解得t=2,
∴运动2秒时,△ABD≌△DCE能成立;
(3)当△ABD≌△DCE时,∠CDE=∠BAD,
又∵∠ADE=180°﹣∠CDE﹣∠ADB,∠B=∠180°﹣∠BAD﹣∠ADB,
∴∠ADE=∠B,
又∵∠BAC=α,AB=AC,
∴∠ADE=∠B=(180°﹣α)=90°﹣α.
故答案为:90°﹣α.
五.解答题(共1小题,满分7分,每小题7分)
24.解:(1)设这项工程的规定时间是x天,则甲队单独施工需要x天完工,乙队单独施工需要1.5x天完工,
依题意,得:
+=1,
解得:x=30,
经检验,x=30是原方程的解,且符合题意.
答:这项工程的规定时间是30天.
(2)由(1)可知:甲队单独施工需要30天完工,乙队单独施工需要45天完工,
1÷(+)=18(天).
答:甲乙两队合作完成该工程需要18天.
六.解答题(共1小题,满分8分,每小题8分)
25.解:作DE⊥AC于E,DF⊥BC于F.
∵CD平分∠ACB,
∴DE=DF,
∵点D是AB的中点,
∵DB=DA,
∴Rt△DBF≌△Rt△DAE(HL),
∴∠DBF=∠DAE,
∴CA=CB,
∴△ABC是等腰三角形,AC=BC=8,
又∵∠ACE=60°,
∴∠ACB=120°,
又CD平分∠ACB,
∴∠BCD=60°,
∵AE∥DC,
∴∠AEC=∠BCD=60°,
∴△ACE是等边三角形,
∴△ACE的周长为24.
同课章节目录
