1.7.1定积分在几何中的应用-人教版高中数学选修2-2课件(24张PPT)
文档属性
| 名称 | 1.7.1定积分在几何中的应用-人教版高中数学选修2-2课件(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览




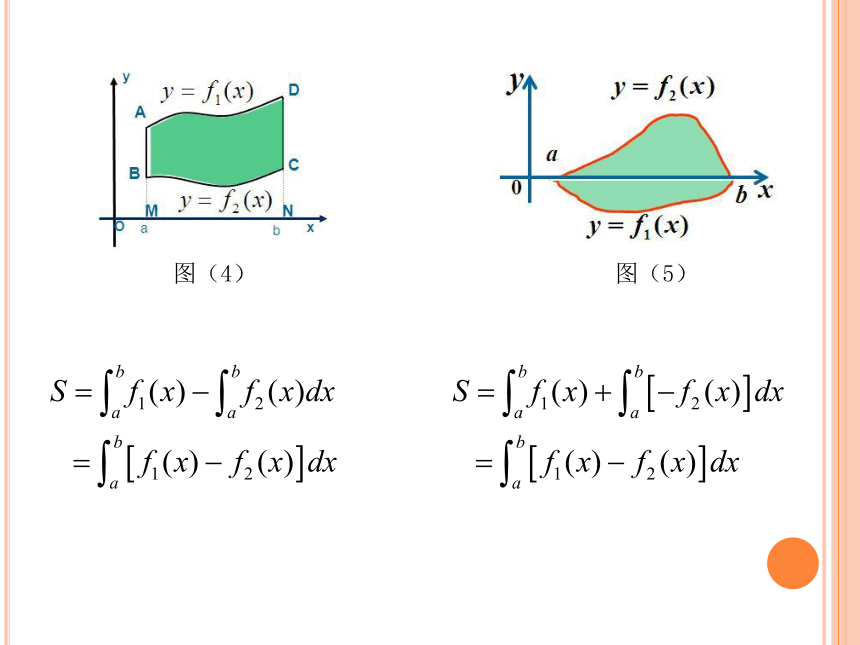
文档简介
河北赵州桥
北京卢沟桥
颐和园绣漪桥
如何计算桥拱通过的水流量?
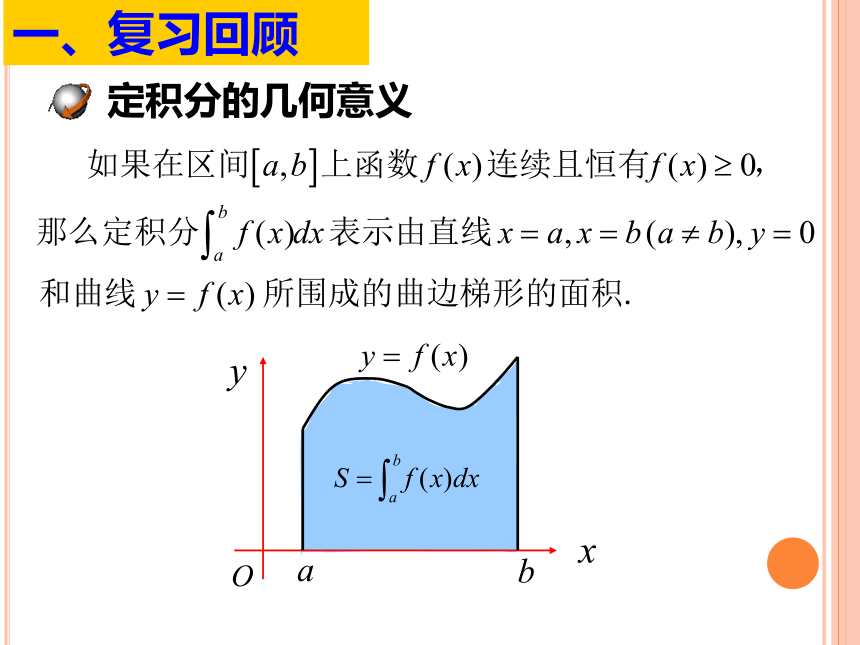
一、复习回顾
定积分的几何意义
x
y
O
a
b
y?f (x)
y?-f (x)
=-S
=-
.
上述曲边梯形面积的负值。
=-S
这个结论叫微积分基本定理(fundamental theorem of calculus),又叫牛顿-莱布尼茨公式(Newton-Leibniz Formula).
设函数f(x)在区间[a,b]上连续,并且 ,则,
微积分基本定理
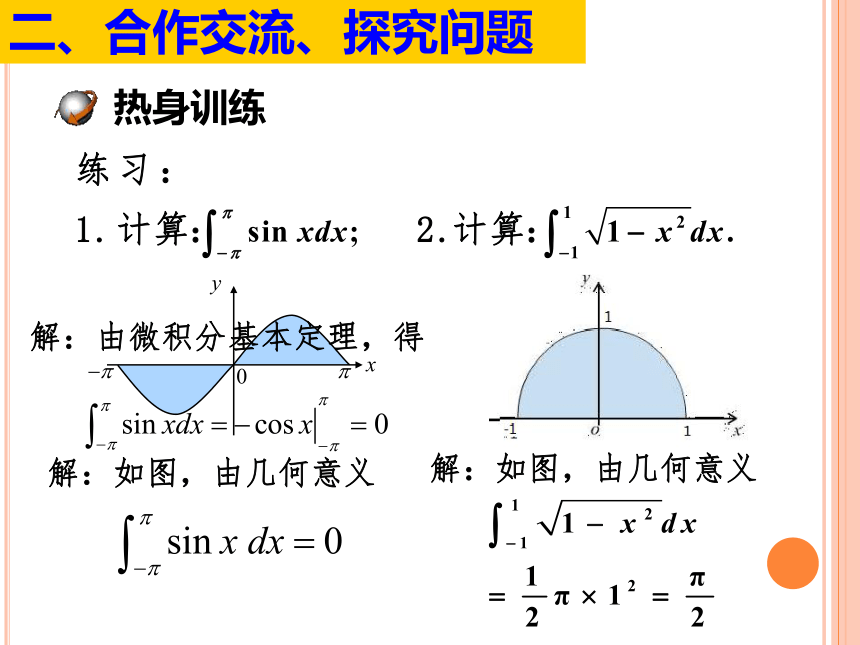
二、合作交流、探究问题
热身训练
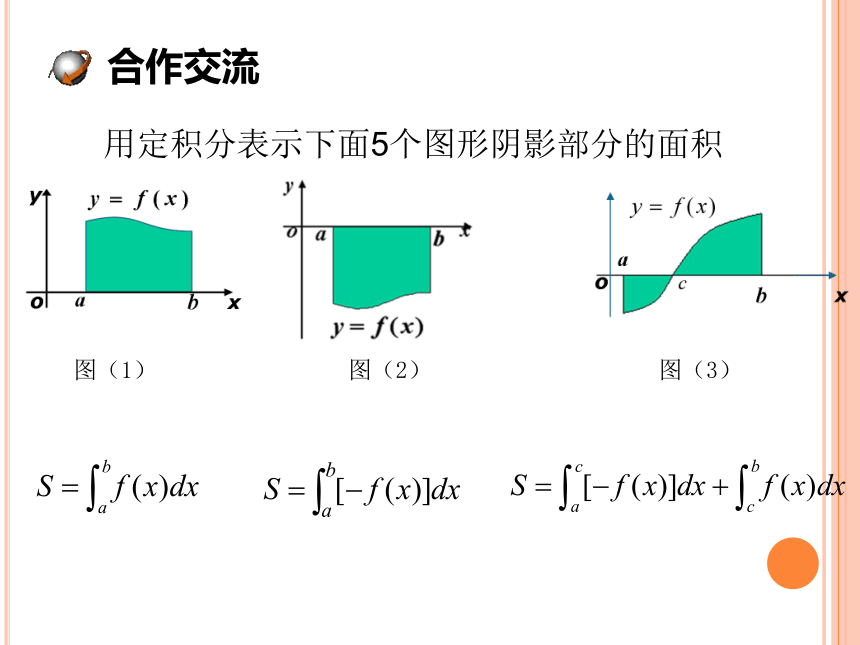
用定积分表示下面5个图形阴影部分的面积
图(1) 图(2) 图(3)
合作交流
图(4) 图(5)
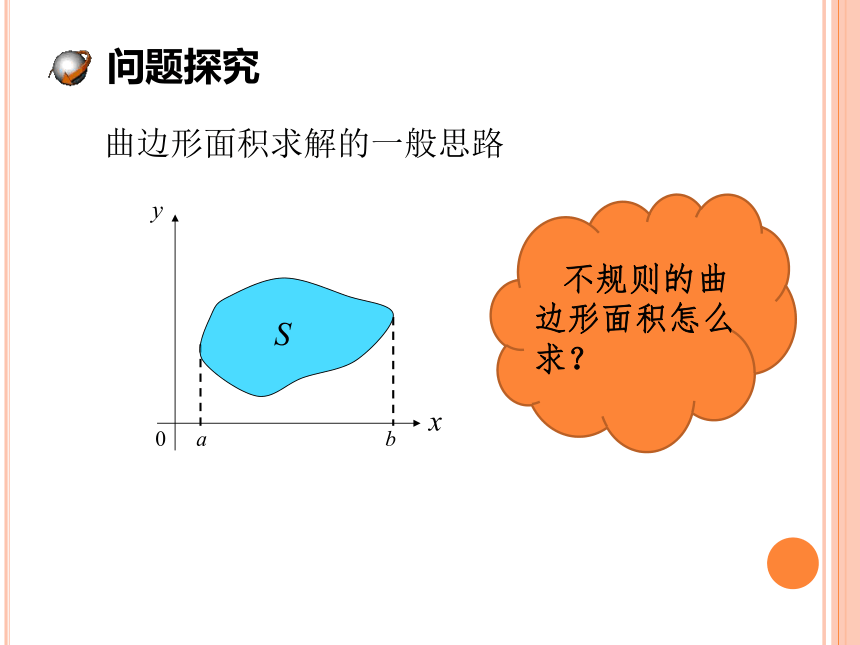
曲边形面积求解的一般思路
不规则的曲边形面积怎么求?
问题探究
曲边形
面积
曲边梯形(三条直边,一条曲边)
三、实践应用、解决问题
x
y
O
A
B
C
D
1
1
-1
-1
解:做出草图,所求面积为
图中阴影部分面积。
8m
4m
方法1
方法2
方法3
归纳
方法1
返回
方法2
返回
返回
方法3
四、巩固总结、拓展提升
求两曲线围成的平面图形的面积的一般步骤:
(1)作出示意图,求交点坐标;
(2)将曲边形面积转化为曲边梯形面积;
(3)合理选取积分变量,被积函数及积分区间;
(4)计算定积分,求出面积.
归纳总结
探究2
探究1
小结
应用提升
探究1
返回
探究2
S3
S1
S2
返回
一个公式
两个方法
两种思想
简单应用
定积分
回归
1、转化与化归的思想方法;
2、数形结合的思想方法。
1、定积分的几何意义求法;
2、微积分基本定理。
五、总结
作业
北京卢沟桥
颐和园绣漪桥
如何计算桥拱通过的水流量?
一、复习回顾
定积分的几何意义
x
y
O
a
b
y?f (x)
y?-f (x)
=-S
=-
.
上述曲边梯形面积的负值。
=-S
这个结论叫微积分基本定理(fundamental theorem of calculus),又叫牛顿-莱布尼茨公式(Newton-Leibniz Formula).
设函数f(x)在区间[a,b]上连续,并且 ,则,
微积分基本定理
二、合作交流、探究问题
热身训练
用定积分表示下面5个图形阴影部分的面积
图(1) 图(2) 图(3)
合作交流
图(4) 图(5)
曲边形面积求解的一般思路
不规则的曲边形面积怎么求?
问题探究
曲边形
面积
曲边梯形(三条直边,一条曲边)
三、实践应用、解决问题
x
y
O
A
B
C
D
1
1
-1
-1
解:做出草图,所求面积为
图中阴影部分面积。
8m
4m
方法1
方法2
方法3
归纳
方法1
返回
方法2
返回
返回
方法3
四、巩固总结、拓展提升
求两曲线围成的平面图形的面积的一般步骤:
(1)作出示意图,求交点坐标;
(2)将曲边形面积转化为曲边梯形面积;
(3)合理选取积分变量,被积函数及积分区间;
(4)计算定积分,求出面积.
归纳总结
探究2
探究1
小结
应用提升
探究1
返回
探究2
S3
S1
S2
返回
一个公式
两个方法
两种思想
简单应用
定积分
回归
1、转化与化归的思想方法;
2、数形结合的思想方法。
1、定积分的几何意义求法;
2、微积分基本定理。
五、总结
作业
