2.1从平面向量到空间向量-北师大版高中数学选修2-1课件(29张PPT)
文档属性
| 名称 | 2.1从平面向量到空间向量-北师大版高中数学选修2-1课件(29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:39:46 | ||
图片预览







文档简介
一. 复习平面向量
1.向量定义:
既有大小又有方向的量叫做向量。
几何表示法:用有向线段表示
字母表示法:
用小写字母表示,或者用表示向量的
有向线段的起点和终点字母表示。
如: a 或AB
2.向量的表示方法:
3.相等向量:
方向相同且模相等的向量.
相反向量:
平行向量:
共线向量:
单位向量:
零向量:
方向相反且模相等的向量.
方向相同或相反的向量.
平行向量也叫共线向量.
模为1个单位的向量.
模为0的向量.
a
a
相反向量
a
b
c
共线向量或平行向量
3、
A
B
C
D
A
B
C
D
a
A
B
C
D
A1
B1
C1
D1
b
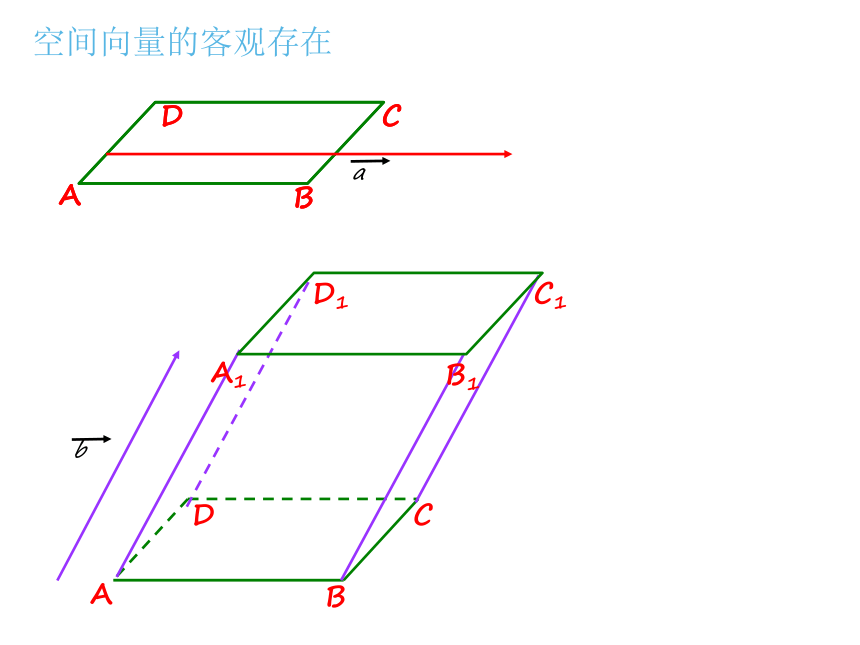
空间向量的客观存在
物理中的事例
如图
F1
F2
F3
一个放在水平面上物体,受到不在同一平面内的三个力的作用,如何求它们的合力?
正东
正北
向上
这需要进一步来认识空间中的向量
F3
F1
F2
如图一块均匀的正三角形钢板质量为500kg,
在它的顶点处分别受F1、F2、F3三个力,每
个力与同它相邻的三角形的两边的夹角都是
60度,且︱F1︱= ︱F2︱ =︱F3︱=200kg。
这块钢板在这些力的作用下将怎样运动?
这三个力至少多大时,才能提起这块钢板?
看下面建筑
这个建筑钢架中有很多向量的身影,但他们有些并不在同一平面内——这就是我们今天要学习的空间向量.
复习回顾:平面向量
定义:
既有大小又有方向的量叫做向量。
用有向线段表示
用小写字母表示,或者用表示
向量的有向线段的起点和终点字母表示
相等向量:
零向量:
单位向量:
相反向量:
长度为0的向量
模为1的向量
长度相等且方向相同的向量
长度相等且方向相反的向量
几何表示法:
字母表示法:
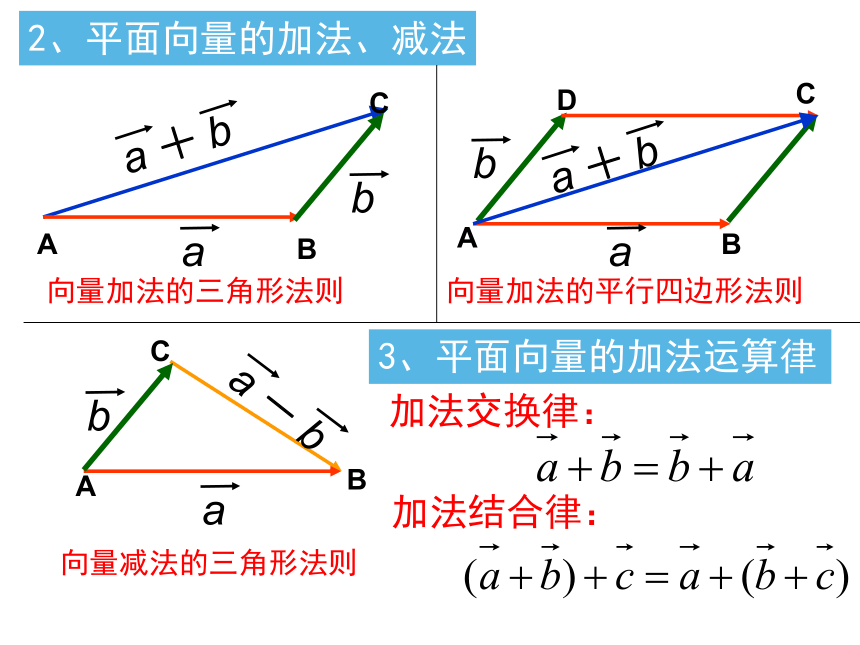
2、平面向量的加法、减法
向量加法的三角形法则
向量加法的平行四边形法则
向量减法的三角形法则
a -
b
a +
b
a
A
B
b
C
a
A
B
b
D
C
a
A
B
b
C
a +
b
3、平面向量的加法运算律
加法交换律:
加法结合律:
在一个平面内来考虑
既有大小又有方向的量称为平面向量
在一个空间内来考虑
既有大小又有方向的量称为空间向量
1.空间向量的概念
可以看出:
平面向量与空间向量只是研究的范围不同.平面向量扩展到空间就是空间向量。
2.空间向量的表示
表示方法1: 用有向线段表示
表示方法2: 用字母表示
a, b, c……
或者 a, b, c……
如 , A叫做向量的起点, B叫做向量的终点;
AB
注意:数学中所讨论的向量与向量的起点无关称之为自由向量。
A
B
3.空间向量的模:
空间向量的大小也叫做向量的长度或模
用∣ ∣或∣ ∣表示。
4.空间两向量的夹角
a
b
b
a
B
O
A
当< , >=?/2时,向量 与 垂直,
a
b
a
b
a
b
记作: ⊥
当< , >=0或?时,向量 与 平行,
a
b
a
b
a
b
记作: //
4.空间两向量的夹角
注意:〈a,b〉=〈b,a〉
平面向量
空间向量
具有大小和方向的量
具有大小和方向的量
几何表示法
几何表示法
字母表示法
字母表示法
向量的大小
向量的大小
长度为零的向量
长度为零的向量
模为1的向量
模为1的向量
长度相等且方向
相反的向量
长度相等且方向
相反的向量
长度相等且方向相同 的向量
长度相等且方向相同的向量
定义
表示法
向量的模
零向量
单位向量
相反向量
相等向量
类比平面向量与空间向量的基本概念
思考交流:
在同一平面
在一个空间
3,4
平面直线的方向向量是如何定义的?直线的方向向量唯一吗?
如何表示空间直线的方向向量?
三 空间直线的方向向量
L
在平面内与直线L共线的向量叫直线的方向向量。
直线的方向向量有无数条。
a
过空间中一定点A,作法向量
为 的平面。
a
a
A
结论:过一点只能做一个平面和已知法向量垂直。
a
b
a
b
O
A
B
b
结论:1.空间任意两个向量都是共面向量,但不确定唯一平面。
2.平面向量中两个向量的有关结论如加、减、数乘、内积仍适用于空间向量。这也是我们后面学习空间向量运算的基础。
思考:空间任意两个向量是否共面?
是否确定唯一的平面?
4.零向量:
规定:长度为0的向量叫做零向量,记作:
5.单位向量:
模为1的向量称为单位向量
当有向线段的起点A与终点B重合时,
6.相反向量:
与向量 长度相等而方向相反的向量,称为 的相反向量。
记作:
7.相等向量:
方向相同且模相等的向量称为相等向量
因此,在空间,同向且等长的有向线段表示同一向量或相等向量。
空间任意两个向量都可以平移到同一平面内,成为同一平面内的两个向量。
平面向量
概念
加法
减法
运算
运
算
律
定义
表示法
相等向量
减法:三角形法则
加法:三角形法则或
平行四边形法则
空间向量的加法、减法运算
空间向量
具有大小和方向的量
加法交换律
加法结合律
a
b
a
b
a
b
+
O
A
B
b
C
空间向量的加减法
a
b
O
A
B
b
a
结论:空间任意两个向量都是共面向量,所以它们可用同一平面内的两条有向线段表示.
因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们.
平面向量
概念
加法
减法
运算
运
算
律
定义
表示法
相等向量
减法:三角形法则
加法:三角形法则或
平行四边形法则
空间向量的加法、减法运算
空间向量
具有大小和方向的量
加法交换律
加法结合律
加法交换律
加法:三角形法则或
平行四边形法则
减法:三角形法则
加法结合律
成立吗?
(1)加法交换律:
(2)加法结合律:
a
b
c
a + b + c
a
b
c
a + b + c
a + b
b + c
空间向量的加法、减法运算
(1)首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:
推广
(2)首尾相接的若干向量构成一个封闭图形,
则它们的和为零向量.即:
推广
对空间向量的加法、减法的说明
⒈ 空间向量的运算就是平面向量运算的推广.
⒉ 两个向量相加的平行四边形法则在空间
仍然成立.
⒊ 空间向量的加法运算可以推广至若干个
向量相加.
说明
A’
B’
C’
D’
A
B
C
D
a
平行六面体的六个面都是平行四边形,每个面的边叫做平行六面体的棱.
平行四边形ABCD平移向量 a 到 的轨迹所形成的几何体,叫做平行六面体.记作ABCD— .
平行六面体
1.向量定义:
既有大小又有方向的量叫做向量。
几何表示法:用有向线段表示
字母表示法:
用小写字母表示,或者用表示向量的
有向线段的起点和终点字母表示。
如: a 或AB
2.向量的表示方法:
3.相等向量:
方向相同且模相等的向量.
相反向量:
平行向量:
共线向量:
单位向量:
零向量:
方向相反且模相等的向量.
方向相同或相反的向量.
平行向量也叫共线向量.
模为1个单位的向量.
模为0的向量.
a
a
相反向量
a
b
c
共线向量或平行向量
3、
A
B
C
D
A
B
C
D
a
A
B
C
D
A1
B1
C1
D1
b
空间向量的客观存在
物理中的事例
如图
F1
F2
F3
一个放在水平面上物体,受到不在同一平面内的三个力的作用,如何求它们的合力?
正东
正北
向上
这需要进一步来认识空间中的向量
F3
F1
F2
如图一块均匀的正三角形钢板质量为500kg,
在它的顶点处分别受F1、F2、F3三个力,每
个力与同它相邻的三角形的两边的夹角都是
60度,且︱F1︱= ︱F2︱ =︱F3︱=200kg。
这块钢板在这些力的作用下将怎样运动?
这三个力至少多大时,才能提起这块钢板?
看下面建筑
这个建筑钢架中有很多向量的身影,但他们有些并不在同一平面内——这就是我们今天要学习的空间向量.
复习回顾:平面向量
定义:
既有大小又有方向的量叫做向量。
用有向线段表示
用小写字母表示,或者用表示
向量的有向线段的起点和终点字母表示
相等向量:
零向量:
单位向量:
相反向量:
长度为0的向量
模为1的向量
长度相等且方向相同的向量
长度相等且方向相反的向量
几何表示法:
字母表示法:
2、平面向量的加法、减法
向量加法的三角形法则
向量加法的平行四边形法则
向量减法的三角形法则
a -
b
a +
b
a
A
B
b
C
a
A
B
b
D
C
a
A
B
b
C
a +
b
3、平面向量的加法运算律
加法交换律:
加法结合律:
在一个平面内来考虑
既有大小又有方向的量称为平面向量
在一个空间内来考虑
既有大小又有方向的量称为空间向量
1.空间向量的概念
可以看出:
平面向量与空间向量只是研究的范围不同.平面向量扩展到空间就是空间向量。
2.空间向量的表示
表示方法1: 用有向线段表示
表示方法2: 用字母表示
a, b, c……
或者 a, b, c……
如 , A叫做向量的起点, B叫做向量的终点;
AB
注意:数学中所讨论的向量与向量的起点无关称之为自由向量。
A
B
3.空间向量的模:
空间向量的大小也叫做向量的长度或模
用∣ ∣或∣ ∣表示。
4.空间两向量的夹角
a
b
b
a
B
O
A
当< , >=?/2时,向量 与 垂直,
a
b
a
b
a
b
记作: ⊥
当< , >=0或?时,向量 与 平行,
a
b
a
b
a
b
记作: //
4.空间两向量的夹角
注意:〈a,b〉=〈b,a〉
平面向量
空间向量
具有大小和方向的量
具有大小和方向的量
几何表示法
几何表示法
字母表示法
字母表示法
向量的大小
向量的大小
长度为零的向量
长度为零的向量
模为1的向量
模为1的向量
长度相等且方向
相反的向量
长度相等且方向
相反的向量
长度相等且方向相同 的向量
长度相等且方向相同的向量
定义
表示法
向量的模
零向量
单位向量
相反向量
相等向量
类比平面向量与空间向量的基本概念
思考交流:
在同一平面
在一个空间
3,4
平面直线的方向向量是如何定义的?直线的方向向量唯一吗?
如何表示空间直线的方向向量?
三 空间直线的方向向量
L
在平面内与直线L共线的向量叫直线的方向向量。
直线的方向向量有无数条。
a
过空间中一定点A,作法向量
为 的平面。
a
a
A
结论:过一点只能做一个平面和已知法向量垂直。
a
b
a
b
O
A
B
b
结论:1.空间任意两个向量都是共面向量,但不确定唯一平面。
2.平面向量中两个向量的有关结论如加、减、数乘、内积仍适用于空间向量。这也是我们后面学习空间向量运算的基础。
思考:空间任意两个向量是否共面?
是否确定唯一的平面?
4.零向量:
规定:长度为0的向量叫做零向量,记作:
5.单位向量:
模为1的向量称为单位向量
当有向线段的起点A与终点B重合时,
6.相反向量:
与向量 长度相等而方向相反的向量,称为 的相反向量。
记作:
7.相等向量:
方向相同且模相等的向量称为相等向量
因此,在空间,同向且等长的有向线段表示同一向量或相等向量。
空间任意两个向量都可以平移到同一平面内,成为同一平面内的两个向量。
平面向量
概念
加法
减法
运算
运
算
律
定义
表示法
相等向量
减法:三角形法则
加法:三角形法则或
平行四边形法则
空间向量的加法、减法运算
空间向量
具有大小和方向的量
加法交换律
加法结合律
a
b
a
b
a
b
+
O
A
B
b
C
空间向量的加减法
a
b
O
A
B
b
a
结论:空间任意两个向量都是共面向量,所以它们可用同一平面内的两条有向线段表示.
因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们.
平面向量
概念
加法
减法
运算
运
算
律
定义
表示法
相等向量
减法:三角形法则
加法:三角形法则或
平行四边形法则
空间向量的加法、减法运算
空间向量
具有大小和方向的量
加法交换律
加法结合律
加法交换律
加法:三角形法则或
平行四边形法则
减法:三角形法则
加法结合律
成立吗?
(1)加法交换律:
(2)加法结合律:
a
b
c
a + b + c
a
b
c
a + b + c
a + b
b + c
空间向量的加法、减法运算
(1)首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:
推广
(2)首尾相接的若干向量构成一个封闭图形,
则它们的和为零向量.即:
推广
对空间向量的加法、减法的说明
⒈ 空间向量的运算就是平面向量运算的推广.
⒉ 两个向量相加的平行四边形法则在空间
仍然成立.
⒊ 空间向量的加法运算可以推广至若干个
向量相加.
说明
A’
B’
C’
D’
A
B
C
D
a
平行六面体的六个面都是平行四边形,每个面的边叫做平行六面体的棱.
平行四边形ABCD平移向量 a 到 的轨迹所形成的几何体,叫做平行六面体.记作ABCD— .
平行六面体
同课章节目录
