3.4.2 圆锥曲线的共同特征-北师大版高中数学选修2-1课件(47张PPT)
文档属性
| 名称 | 3.4.2 圆锥曲线的共同特征-北师大版高中数学选修2-1课件(47张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:44:56 | ||
图片预览









文档简介
3.4.2 圆锥曲线的共同特征
平面内到两定点F1、F2 距离之差的绝对值等于常数2a (2a< |F1F2| )的点的轨迹
平面内到定点F的距离和到定直线的距离相等的点的轨迹
平面内到两定点 F1、F2 距离之和等于常数 2a (2a>|F1F2|)的点的轨迹
温故知新
表达式 |PF1|+|PF2|=2a(2a>|F1F2|)
1、 椭圆的定义:
2 、双曲线的定义:
表达式||PF1|-|PF2||=2a (2a<|F1F2|)
3、抛物线的定义:
表达式|PF|=d (d为动点到定直线距离)
探究与思考:
若PF/d≠1呢?
圆锥曲线的统一定义指的是到定点F的距离与到定直线l的距离(F不在l上)的比e是常数的点的轨迹叫做圆锥曲线。
解:由题意可得:
化简得
(a2-c2)x2+a2y2=a2(a2-c2)
令a2-c2=b2,则上式化为:
所以点P的轨迹是焦点为(-c,0),(c,0),长轴长、短轴长分别为2a,2b的椭圆.
例1.已知点P(x,y)到定点F(c,0)的距离与它到定直
线 的距离的比是常数 (a>c>0),求P的轨迹.
平面内到一定点F 与到一条定直线l 的距离之比为常数 e 的点的轨迹.( 点F 不在直线l 上)
(1)当 0< e <1 时, 点的轨迹是椭圆.
(3)当 e >1 时, 点的轨迹是双曲线.
圆锥曲线统一定义:
(2)当 e = 1 时, 点的轨迹是抛物线.
其中常数e叫做圆锥曲线的离心率,
定点F叫做圆锥曲线的焦点,
定直线l就是该圆锥曲线的准线.
例2.已知双曲线 上一点P到左焦点的距离为14,求P点到右准线的距离.
法一:由已知可得a=8,b=6,c=10.
因为|PF1|=14<2a , 所以P为双曲线左支上一点,
设双曲线左右焦点分别为F1、F2,P到右准线的距离
为d,则由双曲线的定义可得|PF2|-|PF1|=16,
所以|PF2|=30,又由双曲线第二定义可得
所以d= |PF2|=24
定 义
图 形
方 程
范 围
对称性
焦 点
顶 点
离心率
F1
F2
M
y
x
O
y
x
O
M
F1
F2
|MF1|+|MF2|=2a (2a>|F1F2|)
(c,0)、(?c,0)
(0,c)、(0,?c)
(?a,0) (0,?b)
|x|? a |y|?b
|x|? b |y|? a
关于x轴、y轴、原点对称
(?b,0) (0,?a)
一个框,四个点,注意光滑和圆扁,莫忘对称要体现
所以,点M的轨迹是长轴、短轴长分别为10、6的椭圆。
F
l
x
o
y
M
H
d
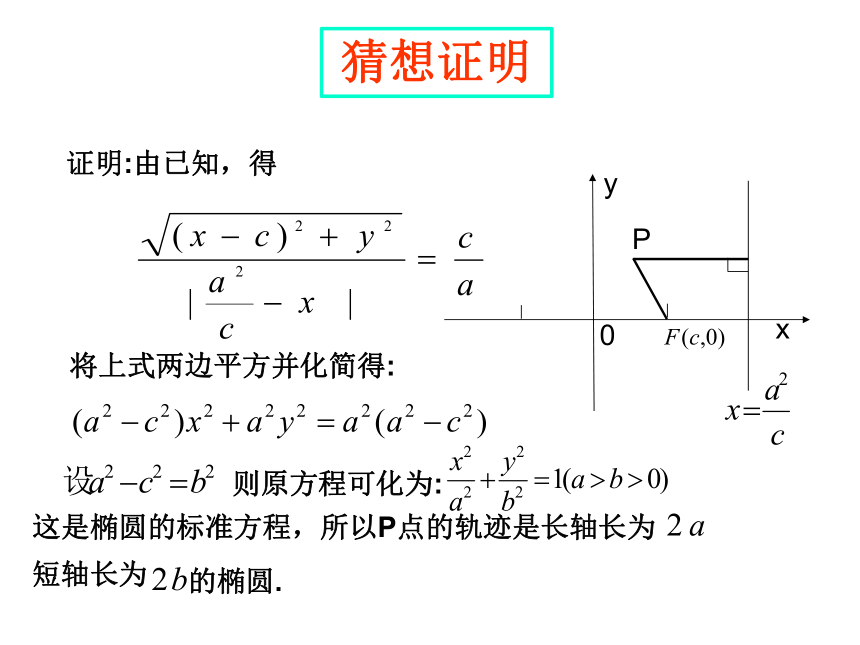
猜想证明
若动点P(x,y)和定点F(c,0)的距离与它到定直线l: 的距离的比是常数 (0猜想
将上式两边平方并化简得:
则原方程可化为:
0
x
y
P
证明:由已知,得
猜想证明
这是椭圆的标准方程,所以P点的轨迹是长轴长为
短轴长为
的椭圆.
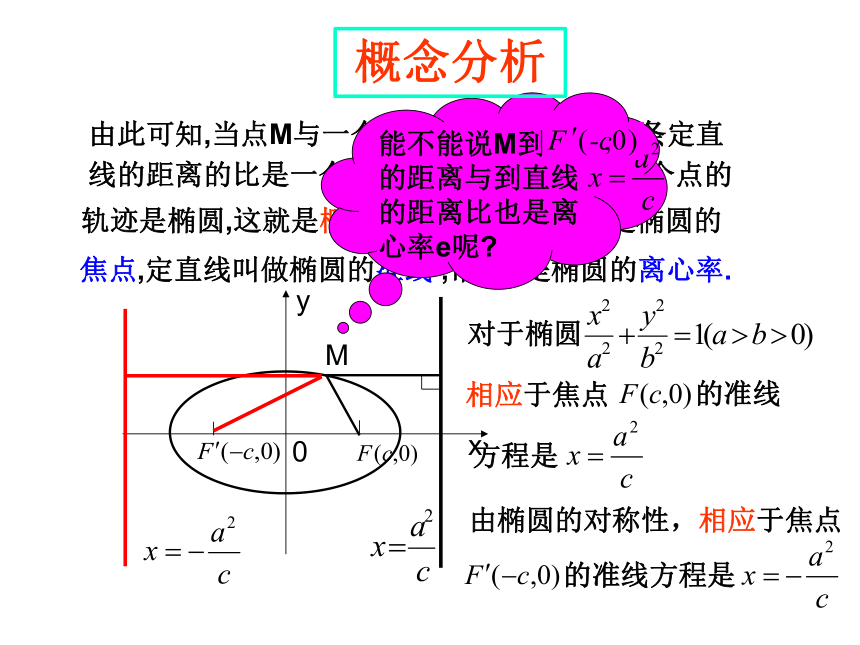
由此可知,当点M与一个定点的距离和它到一条定直
线的距离的比是一个常数
时,这个点的
轨迹是椭圆,这就是椭圆的第二定义,定点是椭圆的
焦点,定直线叫做椭圆的准线,,常数e是椭圆的离心率.
0
x
y
M
对于椭圆
相应于焦点
的准线
方程是
能不能说M到 的距离与到直线
的距离比也是离心率e呢?
)
0
,
(
-c
F
?
概念分析
由椭圆的对称性,相应于焦点
的准线方程是
O
x
y
P
F1
F2
O
y
x
P
F1
F2
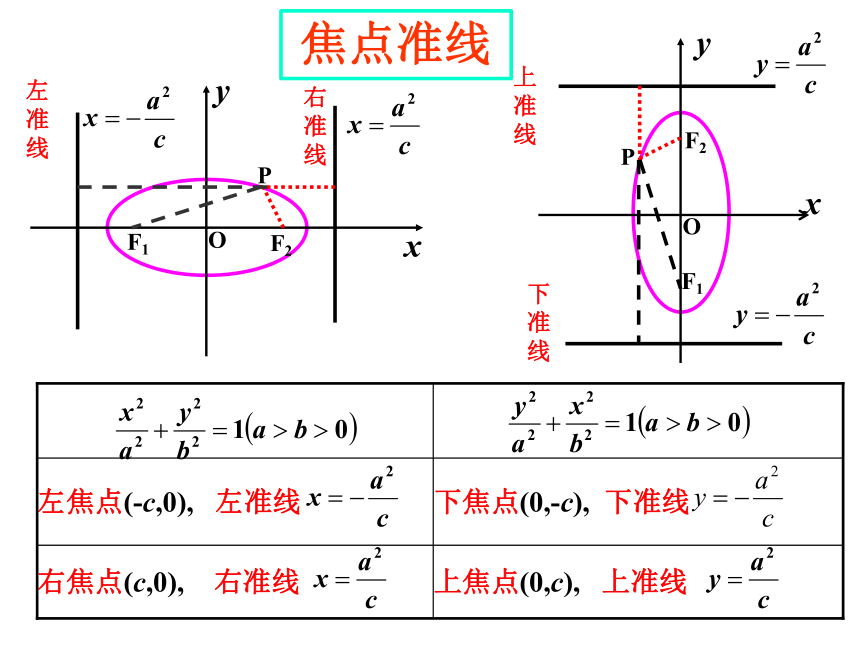
右准线
上准线
下准线
左准线
上焦点(0,c), 上准线
右焦点(c,0), 右准线
下焦点(0,-c), 下准线
左焦点(-c,0), 左准线
焦点准线
例2 求中心在原点,一条准线方程是x=3,
离心率为 的椭圆标准方程.
解:依题意设椭圆标准方程为
由已知有
解得a=
c=
所求椭圆的标准方程为
例题讲解
例3 椭圆方程为 ,其上有一点P,它
到右焦点的距离为14,求P点到左准线的距离.
P
0
x
y
解:由椭圆的方程可知
由第一定义可知:
由第二定义知:
例题讲解
P(x0,y0)是椭圆 (a>b>0)上的一点,F1,F2是左、右焦点,则PF1,PF2叫焦半径,求证∣PF左∣=a+ex0 ∣PF右∣=a-ex0,
例 1
证明:
y
o
P(x0,y0)
x
F1(-C,0)
F1(C,0)
d1
d2
由题意得d1=x0+
d2
=
-
x0
又:
=
=e
=
∴
=ed1=e(x0+
)=
=ed2=e( - x0)=
a+ex0
a-ex0
(法一)
(法二):利用两点距离公式
焦半径:
1)P(x0,y0)是椭圆 (a>b>0)上的一点,F1,F2是左、右焦点,则PF1,PF2叫焦半径∣PF左∣=a+ex0, ∣PF右∣=a-ex0
2)AB过焦点的弦,
=2a+e(XA+XB)
=2a-e(XA+XB)
Rmax=a+c
Rmin=a-c
3)通经:过焦点且与长轴垂直的弦 d
d=
(当焦点在y轴上时----------- )
例2:在椭圆
距离是到右焦点距离的2倍.
=1求一点P使它到左焦点
+
例2:在椭圆
+
=1求一点P使它到左焦点
距离是到右焦点距离的2倍.
解:设P(x0,y0) 由题意得a=5 c=4 e=
=
a+ex0=5+
x0
=5 -
x0
又
=2
∴
5+ X0
=
2( 5 - X0)
∴
X0=
代入
+
=1
得:y0=±
所以 P( , )
±
思考:抛物线的方程为x=ay2(a≠0)求它的焦点坐标和准线方程?
解:抛物线标准方程为:y2= x
1
a
∴2p=
1
a
4a
1
∴焦点坐标是( ,0),准线方程是: x=
4a
1
②当a<0时, , 抛物线的开口向左
p
2
=
1
4a
∴焦点坐标是( ,0),准线方程是: x=
4a
1
1
4a
①当a>0时, , 抛物线的开口向右
p
2
=
1
4a
当a>0时与当a<0时,结论都为:
思考:
二次函数 的图像为什么是抛物线?
当a>0时与当a<0时,结论都为:
例1:(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;
(2)已知抛物线的方程是y = -6x2,
求它的焦点坐标和准线方程;
(3)已知抛物线的焦点坐标是F(0,-2),求它的标准方程。
解:因为p=3,故焦点坐标为(-,0)
准线方程为x=- -.
32
32
1 12
解:方程可化为:x =- -y,故p=-,焦点坐标
为(0, --),准线方程为y= -.
16
1 24
1 24
2
解:因焦点在y轴的负半轴上,且p=4,故其标准方程为:x = - 8y
2
自主探究
2.已知抛物线的标准方程是y2 = -6x ,则它的焦
点坐标是 ,准线方程是 .
3.已知抛物线的方程是y=6ax2(a≠0),则它
的焦点坐标是 ,准线方程是 .
应用:类题一(由方程求有关量)
1.已知抛物线的标准方程是y2 = 6x ,则它的焦
点坐标是 ,准线方程是 .
感悟 :求抛物线的焦点坐标和准线方程要注意两点:
1.先化为标准方程 2. 判断焦点的位置
是一次项系数的
是一次项系数 的相反数
即:准确“定型”
练习:填空(顶点在原点,焦点在坐标轴上)
方程
焦点
准线
开口方向
开口向右
开口向左
开口向上
开口向下
题型一:利用抛物线的定义解题
例1:已知抛物线y2=2x的焦点是F,点P是抛物线上的动点,又有点A(3,2),求|PA|+|PF|的最小值,并求出此时P点的坐标
题型一:利用抛物线的定义解题
例1.(1)已知抛物线的标准方程是 y 2 = 6 x ,求它的焦点坐标及准线方程
题型二:求抛物线方程的方法:-----待定系数法
(2)已知抛物线的焦点坐标是 F(0,-2),求抛物线的标准方程
x
y
o
l
F
(0,-2)
解:(2)因为焦点在y轴的负半轴上,并且
∴所求抛物线的标准方程是 x2 =-8y .
= 2,∴p = 4 ,
F
x
y
o
l
X = 1
解:(3)∵准线方程是 x = 1,
(3)已知抛物线的准线方程为 x = 1 ,求抛物线的标准方程
y 2 =-4 x
题型二:求抛物线方程的方法:-----待定系数法
且焦点在 x 轴的负半轴上,
∴所求抛物线的标准方程是 y2 =-4x .
∴ p =2 ,
x
y
o
(3,2)
解:(4)∵点A(3,2) 在第一象限,
y 2 = x 或 x 2 = y
4
3
9
2
(4)求过点A(3,2)的抛物线的标准方程
∴抛物线的开口方向只能是向右或向上,
设抛物线的标准方程是
y2 = 2px(p>0),
或 x2 = 2py(p>0),
将(3,2)点的坐标分别代入上述方程可得抛物线的标准方程为
题型二:求抛物线方程的方法:-----待定系数法
例1.求一渐近线为3x+4y=0,一个焦点为(4,0)的双曲线的标准方程.
解:
1、定义:平面内到一个
定点F和一条定直线 l 的距
离的比为常数e(0 M的轨迹,叫椭圆。 定点F叫焦点,定直线 l
叫准线。
一、椭圆的第二定义:
(一)知识回顾:
椭圆有两个焦点F1,F2,两条准线 l1 , l2
F1
F2
M
l1
l2
d1
d2
F2(c,0)
O
x
F1 o
y
P
N
?
?
F2
F1
o
x
y
P
?
M
N
y=a2/c
y=-a2/c
M
F2
焦点在X轴上时,
设 P(x0,y0) 是椭圆上的点,则:焦半径公式为:
|PF1|=a+ex0, |PF2|=a-ex0
焦点在y轴上时,
设 P(x0,y0) 是椭圆上的点,则:焦半径公式为:
|PF1|=a +ey0, |PF2|=a-ey0
椭圆 + =1上的点P与其两焦点
F1、F2的连线段分别叫做椭圆的左
焦半径和右焦半径,统称“焦半径”。
左加右减,下加上减
2、定义式:
3、焦半径公式:
焦点在X轴上:|MF1| = a + ex , |MF2| = a - ex
焦点在Y轴上:|MF1| = a + ey , |MF2| = a - ey
左加右减,下加上减
例2、
解:
x
y
.
.
F(5,0)
O
M(x,y)
.
解:
x
y
.
.
F
F ’
O
M
.
双曲线的第二定义:
y
.
.
F
F ’
O
M
.
x
“三定”:
定点是焦点;
定直线是准线;
定值是离心率.(定点不在定直线上)
F1
F2
x
y
两条准线比双曲线的顶点更接近中心
A1
A2
O
F2
例2、
证明:
P
说明:|PF1|, |PF2|称为双曲线的焦半径.
y
.
.
F2
F1
O
.
x
练习
证明:
P
y
.
.
F2
F1
O
.
x
F1
F2
x
y
(二)M2位于双曲线左支
(一)M1位于双曲线右支
焦半径公式:
O
思考:焦点在y轴上呢?
(x, y 互换)
2.两准线间的距离:
1.准线方程:
3.焦准距:焦点到对应准线的距离
4.双曲线的焦半径公式:
点M(x,y)在左支上时: |MF1|=-a-ex, |MF2|=a-ex
点M(x,y)在右支上时: |MF1|=a+ex, |MF2|=-a+ex
常用结论:
设双曲线
的焦点为:
5、通经:过焦点垂直与实轴的弦
课堂练习
的两准线间的距离等于( )
2、双曲线
1
3
4
2
2
=
-
x
y
的焦点坐标、准线方程
1、求双曲线
1
9
16
2
2
=
-
y
x
和离心率,并用第二定义描述该双曲线。
(A) (B) (C) (D)
B
3、
若改为求P到左准线的距离,答案如何?有几种解法?
F1
F2
x
y
O
D
用椭圆的第二定义求解的一个问题,请仿照此题,设计一个用双曲线的第二定义求解的问题,并给出解答。
一个问题:已知点 在椭圆
4.在学习椭圆的知识时,曾解决过这样
内部, 是椭圆的一个焦点,在椭圆上
求一点P,求 的最小值,这是
A
F
P
d
P
d
P
p
x
y
o
.
F
.
A
.
M
y
.
.
F2
F1
O
.
x
例2.已知双曲线 上一点P到左焦点
的距离为14,求P点到右准线的距离.
平面内到两定点F1、F2 距离之差的绝对值等于常数2a (2a< |F1F2| )的点的轨迹
平面内到定点F的距离和到定直线的距离相等的点的轨迹
平面内到两定点 F1、F2 距离之和等于常数 2a (2a>|F1F2|)的点的轨迹
温故知新
表达式 |PF1|+|PF2|=2a(2a>|F1F2|)
1、 椭圆的定义:
2 、双曲线的定义:
表达式||PF1|-|PF2||=2a (2a<|F1F2|)
3、抛物线的定义:
表达式|PF|=d (d为动点到定直线距离)
探究与思考:
若PF/d≠1呢?
圆锥曲线的统一定义指的是到定点F的距离与到定直线l的距离(F不在l上)的比e是常数的点的轨迹叫做圆锥曲线。
解:由题意可得:
化简得
(a2-c2)x2+a2y2=a2(a2-c2)
令a2-c2=b2,则上式化为:
所以点P的轨迹是焦点为(-c,0),(c,0),长轴长、短轴长分别为2a,2b的椭圆.
例1.已知点P(x,y)到定点F(c,0)的距离与它到定直
线 的距离的比是常数 (a>c>0),求P的轨迹.
平面内到一定点F 与到一条定直线l 的距离之比为常数 e 的点的轨迹.( 点F 不在直线l 上)
(1)当 0< e <1 时, 点的轨迹是椭圆.
(3)当 e >1 时, 点的轨迹是双曲线.
圆锥曲线统一定义:
(2)当 e = 1 时, 点的轨迹是抛物线.
其中常数e叫做圆锥曲线的离心率,
定点F叫做圆锥曲线的焦点,
定直线l就是该圆锥曲线的准线.
例2.已知双曲线 上一点P到左焦点的距离为14,求P点到右准线的距离.
法一:由已知可得a=8,b=6,c=10.
因为|PF1|=14<2a , 所以P为双曲线左支上一点,
设双曲线左右焦点分别为F1、F2,P到右准线的距离
为d,则由双曲线的定义可得|PF2|-|PF1|=16,
所以|PF2|=30,又由双曲线第二定义可得
所以d= |PF2|=24
定 义
图 形
方 程
范 围
对称性
焦 点
顶 点
离心率
F1
F2
M
y
x
O
y
x
O
M
F1
F2
|MF1|+|MF2|=2a (2a>|F1F2|)
(c,0)、(?c,0)
(0,c)、(0,?c)
(?a,0) (0,?b)
|x|? a |y|?b
|x|? b |y|? a
关于x轴、y轴、原点对称
(?b,0) (0,?a)
一个框,四个点,注意光滑和圆扁,莫忘对称要体现
所以,点M的轨迹是长轴、短轴长分别为10、6的椭圆。
F
l
x
o
y
M
H
d
猜想证明
若动点P(x,y)和定点F(c,0)的距离与它到定直线l: 的距离的比是常数 (0
将上式两边平方并化简得:
则原方程可化为:
0
x
y
P
证明:由已知,得
猜想证明
这是椭圆的标准方程,所以P点的轨迹是长轴长为
短轴长为
的椭圆.
由此可知,当点M与一个定点的距离和它到一条定直
线的距离的比是一个常数
时,这个点的
轨迹是椭圆,这就是椭圆的第二定义,定点是椭圆的
焦点,定直线叫做椭圆的准线,,常数e是椭圆的离心率.
0
x
y
M
对于椭圆
相应于焦点
的准线
方程是
能不能说M到 的距离与到直线
的距离比也是离心率e呢?
)
0
,
(
-c
F
?
概念分析
由椭圆的对称性,相应于焦点
的准线方程是
O
x
y
P
F1
F2
O
y
x
P
F1
F2
右准线
上准线
下准线
左准线
上焦点(0,c), 上准线
右焦点(c,0), 右准线
下焦点(0,-c), 下准线
左焦点(-c,0), 左准线
焦点准线
例2 求中心在原点,一条准线方程是x=3,
离心率为 的椭圆标准方程.
解:依题意设椭圆标准方程为
由已知有
解得a=
c=
所求椭圆的标准方程为
例题讲解
例3 椭圆方程为 ,其上有一点P,它
到右焦点的距离为14,求P点到左准线的距离.
P
0
x
y
解:由椭圆的方程可知
由第一定义可知:
由第二定义知:
例题讲解
P(x0,y0)是椭圆 (a>b>0)上的一点,F1,F2是左、右焦点,则PF1,PF2叫焦半径,求证∣PF左∣=a+ex0 ∣PF右∣=a-ex0,
例 1
证明:
y
o
P(x0,y0)
x
F1(-C,0)
F1(C,0)
d1
d2
由题意得d1=x0+
d2
=
-
x0
又:
=
=e
=
∴
=ed1=e(x0+
)=
=ed2=e( - x0)=
a+ex0
a-ex0
(法一)
(法二):利用两点距离公式
焦半径:
1)P(x0,y0)是椭圆 (a>b>0)上的一点,F1,F2是左、右焦点,则PF1,PF2叫焦半径∣PF左∣=a+ex0, ∣PF右∣=a-ex0
2)AB过焦点的弦,
=2a+e(XA+XB)
=2a-e(XA+XB)
Rmax=a+c
Rmin=a-c
3)通经:过焦点且与长轴垂直的弦 d
d=
(当焦点在y轴上时----------- )
例2:在椭圆
距离是到右焦点距离的2倍.
=1求一点P使它到左焦点
+
例2:在椭圆
+
=1求一点P使它到左焦点
距离是到右焦点距离的2倍.
解:设P(x0,y0) 由题意得a=5 c=4 e=
=
a+ex0=5+
x0
=5 -
x0
又
=2
∴
5+ X0
=
2( 5 - X0)
∴
X0=
代入
+
=1
得:y0=±
所以 P( , )
±
思考:抛物线的方程为x=ay2(a≠0)求它的焦点坐标和准线方程?
解:抛物线标准方程为:y2= x
1
a
∴2p=
1
a
4a
1
∴焦点坐标是( ,0),准线方程是: x=
4a
1
②当a<0时, , 抛物线的开口向左
p
2
=
1
4a
∴焦点坐标是( ,0),准线方程是: x=
4a
1
1
4a
①当a>0时, , 抛物线的开口向右
p
2
=
1
4a
当a>0时与当a<0时,结论都为:
思考:
二次函数 的图像为什么是抛物线?
当a>0时与当a<0时,结论都为:
例1:(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;
(2)已知抛物线的方程是y = -6x2,
求它的焦点坐标和准线方程;
(3)已知抛物线的焦点坐标是F(0,-2),求它的标准方程。
解:因为p=3,故焦点坐标为(-,0)
准线方程为x=- -.
32
32
1 12
解:方程可化为:x =- -y,故p=-,焦点坐标
为(0, --),准线方程为y= -.
16
1 24
1 24
2
解:因焦点在y轴的负半轴上,且p=4,故其标准方程为:x = - 8y
2
自主探究
2.已知抛物线的标准方程是y2 = -6x ,则它的焦
点坐标是 ,准线方程是 .
3.已知抛物线的方程是y=6ax2(a≠0),则它
的焦点坐标是 ,准线方程是 .
应用:类题一(由方程求有关量)
1.已知抛物线的标准方程是y2 = 6x ,则它的焦
点坐标是 ,准线方程是 .
感悟 :求抛物线的焦点坐标和准线方程要注意两点:
1.先化为标准方程 2. 判断焦点的位置
是一次项系数的
是一次项系数 的相反数
即:准确“定型”
练习:填空(顶点在原点,焦点在坐标轴上)
方程
焦点
准线
开口方向
开口向右
开口向左
开口向上
开口向下
题型一:利用抛物线的定义解题
例1:已知抛物线y2=2x的焦点是F,点P是抛物线上的动点,又有点A(3,2),求|PA|+|PF|的最小值,并求出此时P点的坐标
题型一:利用抛物线的定义解题
例1.(1)已知抛物线的标准方程是 y 2 = 6 x ,求它的焦点坐标及准线方程
题型二:求抛物线方程的方法:-----待定系数法
(2)已知抛物线的焦点坐标是 F(0,-2),求抛物线的标准方程
x
y
o
l
F
(0,-2)
解:(2)因为焦点在y轴的负半轴上,并且
∴所求抛物线的标准方程是 x2 =-8y .
= 2,∴p = 4 ,
F
x
y
o
l
X = 1
解:(3)∵准线方程是 x = 1,
(3)已知抛物线的准线方程为 x = 1 ,求抛物线的标准方程
y 2 =-4 x
题型二:求抛物线方程的方法:-----待定系数法
且焦点在 x 轴的负半轴上,
∴所求抛物线的标准方程是 y2 =-4x .
∴ p =2 ,
x
y
o
(3,2)
解:(4)∵点A(3,2) 在第一象限,
y 2 = x 或 x 2 = y
4
3
9
2
(4)求过点A(3,2)的抛物线的标准方程
∴抛物线的开口方向只能是向右或向上,
设抛物线的标准方程是
y2 = 2px(p>0),
或 x2 = 2py(p>0),
将(3,2)点的坐标分别代入上述方程可得抛物线的标准方程为
题型二:求抛物线方程的方法:-----待定系数法
例1.求一渐近线为3x+4y=0,一个焦点为(4,0)的双曲线的标准方程.
解:
1、定义:平面内到一个
定点F和一条定直线 l 的距
离的比为常数e(0
叫准线。
一、椭圆的第二定义:
(一)知识回顾:
椭圆有两个焦点F1,F2,两条准线 l1 , l2
F1
F2
M
l1
l2
d1
d2
F2(c,0)
O
x
F1 o
y
P
N
?
?
F2
F1
o
x
y
P
?
M
N
y=a2/c
y=-a2/c
M
F2
焦点在X轴上时,
设 P(x0,y0) 是椭圆上的点,则:焦半径公式为:
|PF1|=a+ex0, |PF2|=a-ex0
焦点在y轴上时,
设 P(x0,y0) 是椭圆上的点,则:焦半径公式为:
|PF1|=a +ey0, |PF2|=a-ey0
椭圆 + =1上的点P与其两焦点
F1、F2的连线段分别叫做椭圆的左
焦半径和右焦半径,统称“焦半径”。
左加右减,下加上减
2、定义式:
3、焦半径公式:
焦点在X轴上:|MF1| = a + ex , |MF2| = a - ex
焦点在Y轴上:|MF1| = a + ey , |MF2| = a - ey
左加右减,下加上减
例2、
解:
x
y
.
.
F(5,0)
O
M(x,y)
.
解:
x
y
.
.
F
F ’
O
M
.
双曲线的第二定义:
y
.
.
F
F ’
O
M
.
x
“三定”:
定点是焦点;
定直线是准线;
定值是离心率.(定点不在定直线上)
F1
F2
x
y
两条准线比双曲线的顶点更接近中心
A1
A2
O
F2
例2、
证明:
P
说明:|PF1|, |PF2|称为双曲线的焦半径.
y
.
.
F2
F1
O
.
x
练习
证明:
P
y
.
.
F2
F1
O
.
x
F1
F2
x
y
(二)M2位于双曲线左支
(一)M1位于双曲线右支
焦半径公式:
O
思考:焦点在y轴上呢?
(x, y 互换)
2.两准线间的距离:
1.准线方程:
3.焦准距:焦点到对应准线的距离
4.双曲线的焦半径公式:
点M(x,y)在左支上时: |MF1|=-a-ex, |MF2|=a-ex
点M(x,y)在右支上时: |MF1|=a+ex, |MF2|=-a+ex
常用结论:
设双曲线
的焦点为:
5、通经:过焦点垂直与实轴的弦
课堂练习
的两准线间的距离等于( )
2、双曲线
1
3
4
2
2
=
-
x
y
的焦点坐标、准线方程
1、求双曲线
1
9
16
2
2
=
-
y
x
和离心率,并用第二定义描述该双曲线。
(A) (B) (C) (D)
B
3、
若改为求P到左准线的距离,答案如何?有几种解法?
F1
F2
x
y
O
D
用椭圆的第二定义求解的一个问题,请仿照此题,设计一个用双曲线的第二定义求解的问题,并给出解答。
一个问题:已知点 在椭圆
4.在学习椭圆的知识时,曾解决过这样
内部, 是椭圆的一个焦点,在椭圆上
求一点P,求 的最小值,这是
A
F
P
d
P
d
P
p
x
y
o
.
F
.
A
.
M
y
.
.
F2
F1
O
.
x
例2.已知双曲线 上一点P到左焦点
的距离为14,求P点到右准线的距离.
同课章节目录
