4.5.2用二分法求方程的近似解-【新教材】人教A版(2019)高中数学必修第一册课件(17张PPT)
文档属性
| 名称 | 4.5.2用二分法求方程的近似解-【新教材】人教A版(2019)高中数学必修第一册课件(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 17.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:48:34 | ||
图片预览



文档简介
4.5.2用二分法求方程的近似解
人教A版高中数学必修第一册
广信数学组
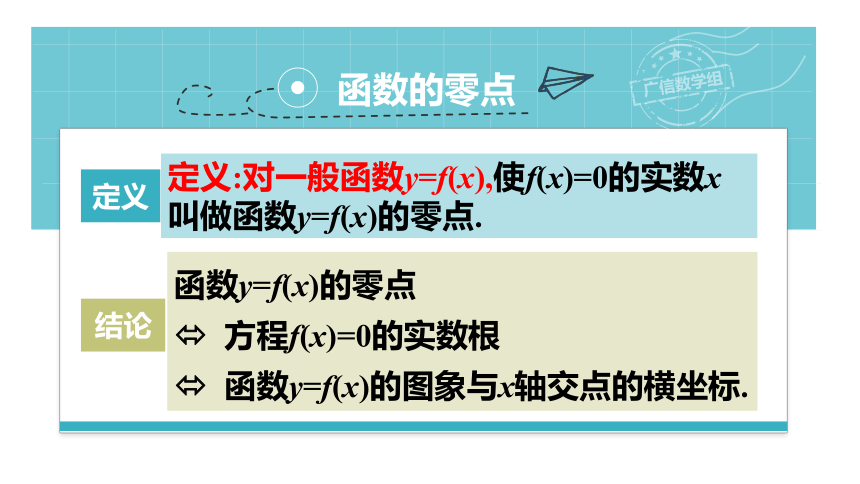
函数的零点
定义
结论
广信数学组
定义:对一般函数y=f(x),使f(x)=0的实数x叫做函数y=f(x)的零点.
函数y=f(x)的零点
? 方程f(x)=0的实数根
? 函数y=f(x)的图象与x轴交点的横坐标.
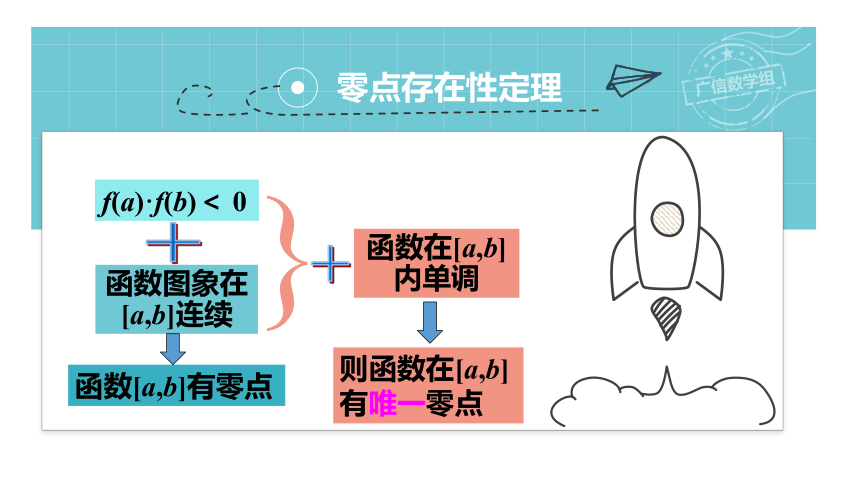
零点存在性定理
f(a)·f(b)< 0
+
函数图象在[a,b]连续
函数[a,b]有零点
+
则函数在[a,b]有唯一零点
函数在[a,b]内单调
}
广信数学组
求方程的近似解
广信数学组
求方程lnx+2x-6=0的近似解
思路
你会求方程 lnx+2x-6=0的根吗?
我们已经知道它在(2,3)有且只有一个解
函数的零点问题
求方程根的问题
求函数f(x)=lnx+2x-6在区间(2,3)内零点的近似值.
广信数学组
现有16枚金币,其中1枚较轻.给你一个天平,问至少需要称几次,才能一定找出这枚较轻的金币?
探索问题 提取原理
广信数学组
我在这里
探索问题 提取原理
广信数学组
我在这里
探索问题 提取原理
广信数学组
我在这里
探索问题 提取原理
广信数学组
哦,找到了啊!
探索问题 提取原理
探索问题 提取原理
广信数学组
某个雷电交加的夜晚,医院的医生正在抢救一个危重病人,忽然电停了,医院采取了应急措施。据了解原因是供电站到医院的某处线路出现了故障,维修工如何迅速查出故障所在? (线路长10km,每50m一棵电线杆)
如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次电线杆子10km长,大约有200根电线杆子。
? 维修线路的工人师傅怎样工作合理?
广信数学组
探索问题 提取原理
如图,设供电站和医院的所在处分别为点A、B(间距10km)
A
(供电站)
这样每查一次,就可以把待查的线路长度缩减一半
C
B
(医院)
D
E
要把故障可能发生的范围缩小到50m~100m左右,即一两根电杆附近,最多查几次就可以了?
算一算
7次
取中点
01
02
03
求近似值
取区间中点,将区间分半
验证零点所在区间,缩小范围
确定近似值
求函数f(x)=lnx+2x-6在区间(2,3)内零点的近似值.
什么时候终止范围的缩小?
依据是什么?
广信数学组
探索问题 提取原理
2
3
取区间中点,将区间分半
2.5
若f(2.5)=0,则函数零点为2.5
若f(2.5)≠0,怎么判断函数的零点在区间(2,2.5)还是(2.5,3)
判断条件:区间端点函数值异号f(a)·f(b)<0
次数
区间长度:
1
2
3
4
0.5
所以方程的近似解为:
2.5
-0.084
2.5
3
0.25
0.125
0.0625
2.75
0.512
2.625
0.215
0.066
2.5625
2.5
2.75
2
3
由于|2.5625-2.5|=0.0625<0.1
2.5
2.75
2.65
2.5625
初始区间(2,3)且f(2)<0,f(3)>0
所以我们可将此区间内的任意一点作为函数零点的近似值,特别地,可以将区间端点作为零点的近似值.
二分法概念
对于在区间[a,b]上连续不断且f(a).f(b)<0的函数y=f(x) ,通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
x
y
0
a
b
二分法的理论依据是什么?
想一想?
零点存在定理
用二分法求函数零点的的近似值的步骤
2.求区间(a,b)的中点c
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
3.计算f(c)
(1)若f(c)=0,则c就是函数的零点;
(3)若f(c)· f(b)<0,则令a= c(此时零点x0∈( c, b) )
(2)若f(a)· f(c)<0,则令b= c(此时零点x0∈(a, c) );
4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2~4.
谢谢
1806
人教A版高中数学必修第一册
广信数学组
函数的零点
定义
结论
广信数学组
定义:对一般函数y=f(x),使f(x)=0的实数x叫做函数y=f(x)的零点.
函数y=f(x)的零点
? 方程f(x)=0的实数根
? 函数y=f(x)的图象与x轴交点的横坐标.
零点存在性定理
f(a)·f(b)< 0
+
函数图象在[a,b]连续
函数[a,b]有零点
+
则函数在[a,b]有唯一零点
函数在[a,b]内单调
}
广信数学组
求方程的近似解
广信数学组
求方程lnx+2x-6=0的近似解
思路
你会求方程 lnx+2x-6=0的根吗?
我们已经知道它在(2,3)有且只有一个解
函数的零点问题
求方程根的问题
求函数f(x)=lnx+2x-6在区间(2,3)内零点的近似值.
广信数学组
现有16枚金币,其中1枚较轻.给你一个天平,问至少需要称几次,才能一定找出这枚较轻的金币?
探索问题 提取原理
广信数学组
我在这里
探索问题 提取原理
广信数学组
我在这里
探索问题 提取原理
广信数学组
我在这里
探索问题 提取原理
广信数学组
哦,找到了啊!
探索问题 提取原理
探索问题 提取原理
广信数学组
某个雷电交加的夜晚,医院的医生正在抢救一个危重病人,忽然电停了,医院采取了应急措施。据了解原因是供电站到医院的某处线路出现了故障,维修工如何迅速查出故障所在? (线路长10km,每50m一棵电线杆)
如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次电线杆子10km长,大约有200根电线杆子。
? 维修线路的工人师傅怎样工作合理?
广信数学组
探索问题 提取原理
如图,设供电站和医院的所在处分别为点A、B(间距10km)
A
(供电站)
这样每查一次,就可以把待查的线路长度缩减一半
C
B
(医院)
D
E
要把故障可能发生的范围缩小到50m~100m左右,即一两根电杆附近,最多查几次就可以了?
算一算
7次
取中点
01
02
03
求近似值
取区间中点,将区间分半
验证零点所在区间,缩小范围
确定近似值
求函数f(x)=lnx+2x-6在区间(2,3)内零点的近似值.
什么时候终止范围的缩小?
依据是什么?
广信数学组
探索问题 提取原理
2
3
取区间中点,将区间分半
2.5
若f(2.5)=0,则函数零点为2.5
若f(2.5)≠0,怎么判断函数的零点在区间(2,2.5)还是(2.5,3)
判断条件:区间端点函数值异号f(a)·f(b)<0
次数
区间长度:
1
2
3
4
0.5
所以方程的近似解为:
2.5
-0.084
2.5
3
0.25
0.125
0.0625
2.75
0.512
2.625
0.215
0.066
2.5625
2.5
2.75
2
3
由于|2.5625-2.5|=0.0625<0.1
2.5
2.75
2.65
2.5625
初始区间(2,3)且f(2)<0,f(3)>0
所以我们可将此区间内的任意一点作为函数零点的近似值,特别地,可以将区间端点作为零点的近似值.
二分法概念
对于在区间[a,b]上连续不断且f(a).f(b)<0的函数y=f(x) ,通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
x
y
0
a
b
二分法的理论依据是什么?
想一想?
零点存在定理
用二分法求函数零点的的近似值的步骤
2.求区间(a,b)的中点c
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
3.计算f(c)
(1)若f(c)=0,则c就是函数的零点;
(3)若f(c)· f(b)<0,则令a= c(此时零点x0∈( c, b) )
(2)若f(a)· f(c)<0,则令b= c(此时零点x0∈(a, c) );
4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2~4.
谢谢
1806
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
