4.5.1函数的零点与方程的解-【新教材】人教A版(2019)高中数学必修第一册课件(31张PPT)
文档属性
| 名称 | 4.5.1函数的零点与方程的解-【新教材】人教A版(2019)高中数学必修第一册课件(31张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 37.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览







文档简介
人教A版高中数学必修第一册
4.5.1函数的零点与方程的解
hán shù de línɡ diǎn yǔ fānɡ chénɡ de jiě
今天我们可以从教科书中了解各式各样方程的解法,但在数学发展史上,方程的求解却经历了相当漫长的岁月.
约公元50-100年前编成的《九章算术》给出了一次方程、二次方程和正系数三次方程的求根方法.
13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法.
阿拉伯数学家花拉子米(约780~约850)给出了一次方程和二次方程的一般解法.
阿贝尔(1802~1829)挪威数学家.证明了五次以上一般方程没有求根公式.
卡尔达诺,意大利数学家,他第一个发
表了三次代数方程一般解法的卡尔达诺
公式,也称卡当公式(解法的思路来自
塔塔利亚,两人因此结怨,争论多年)。
他的学生费拉里第一个求出四次方程的
代数解。
韦达是法国十六世纪最有影响的数学家之
一。第一个引进系统的代数符号,并对方
程论做了改进。韦达讨论了方程根的各种
有理变换,发现了方程根与系数之间的关
系即“韦达定理” 。
初步探索 直观感知chū bù tàn suǒ zhí ɡuān ɡǎn zhī
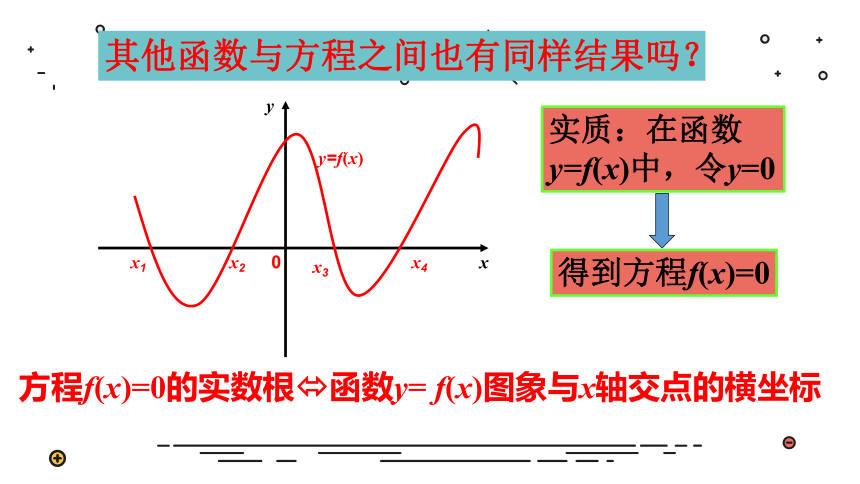
1.求下列方程的根.
①x-2=0 ②x2-2x-3=0 ③log2x=0
2.画出下列函数的图象
①y=x-2 ②x2-2x-3=0 ③y=log2x
3
2
1
-1
-1
2
1
0
1
-1
-2
-1
-2
2
1
0
方程的根就是对应函数图象与x轴交点的横坐标
x
y
O
-1
3
思考:方程根与相应函数图象有什么联系?
其他函数与方程之间也有同样结果吗?
方程f(x)=0的实数根?函数y= f(x)图象与x轴交点的横坐标
0
x
y
x1
x2
x3
x4
y=f(x)
得到方程f(x)=0
实质:在函数y=f(x)中,令y=0
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点。
函数零点的定义:
零点是一个点吗?
注意: 函数的零点是一个实数,当自变量取该值时,其函数值等于零.
区别:
零点对于函数而言,根对于方程而言.
函数y=f(x)的零点与、方程f(x)=0的根、函数y=f(x)的图像与x轴的交点的横坐标的关系.
函数y=f(x)的零点
? 方程f(x)=0的实数根
? 函数y=f(x)的图象与x轴交点的横坐标.
探究 如何求函数的零点?
练习1:求下列函数的零点
1 方程法
2 图象法
思考:函数f(x)=lnx+2x-6是否有零点?如何判断?零点的个数?
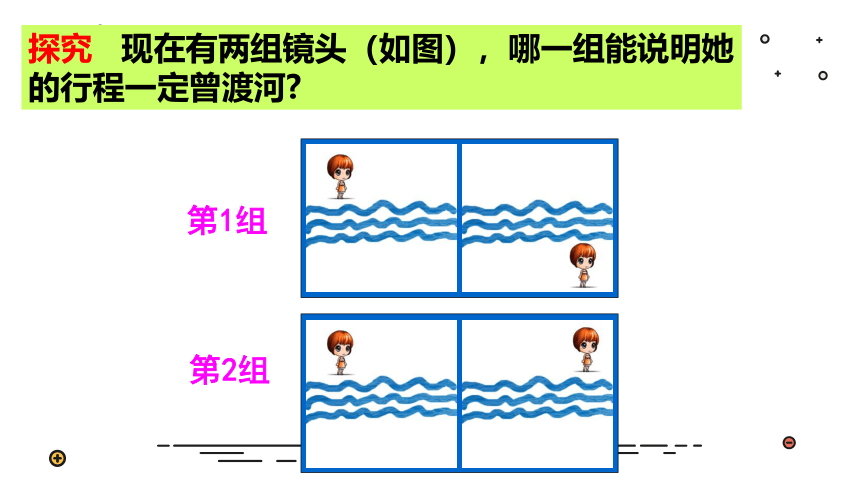
第1组
第2组
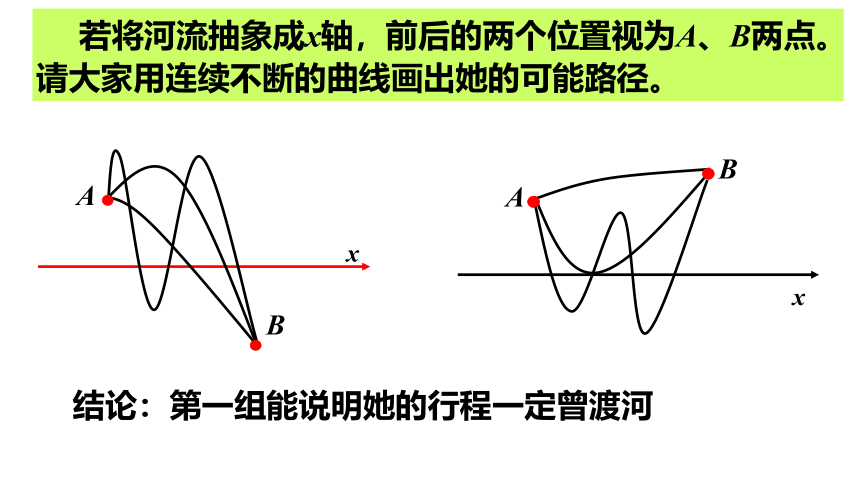
探究 现在有两组镜头(如图),哪一组能说明她的行程一定曾渡河? ??
A
B
B
A
x
x
结论:第一组能说明她的行程一定曾渡河
若将河流抽象成x轴,前后的两个位置视为A、B两点。请大家用连续不断的曲线画出她的可能路径。
x
A
B
O
y
a
b
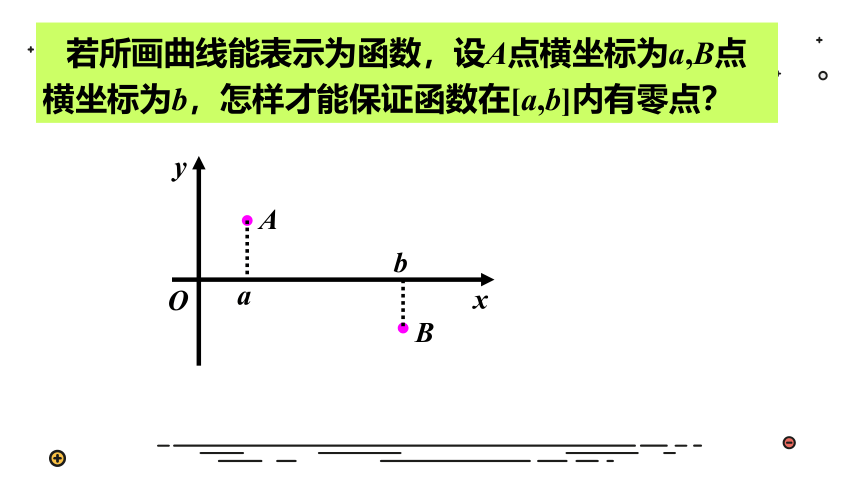
若所画曲线能表示为函数,设A点横坐标为a,B点横坐标为b,怎样才能保证函数在[a,b]内有零点?
a
b
a
A
B
B
A
若所画曲线能表示为函数,设A点横坐标为a,B点横坐标为b,怎样才能保证函数在[a,b]内有零点?
x
b
x
1. 一定有?有几个?一定没有?
2.怎样用数学符号表示零点存在的条件?
y
y
f(a)·f(b) < 0,即端点函数值异号
0
y
x
0
y
x
如果f(a)·f(b) < 0,但图象不是连续不断的,能否一定有零点?
端点函数值异号f(a)·f(b) < 0
+
函数图象连续
则函数有零点
如果函数y =f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且f(a) ·f(b)<0,则函数在(a,b)内有零点.即存在c∈(a,b),使得f(c)=0,这个c也就是方程的根.
零点存在性定理
注:只有上述两个条件同时满足,才能判断函数在指定区间内存在零点。
函数图像连续不断和f(a) ·f(b)<0是函数存在零点的充分条件
是不是必要条件?
函数存在零点 ? 函数图像连续不断和f(a) ·f(b)<0
?
[思考]
(1)若函数y=f(x)在区间(a,b)内有零点,且f(a)·f(b)<0则一定能够得出f(x)在[a,b]上连续么?
不一定
x
a
b
c1
c2
y
x
a
b
c1
c2
y
(2)函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,若函数y=f(x)在区间(a, b)内有零点,一定能得出f(a)·f(b)<0的结论吗?
“函数图像在给定区间[a,b]上连续”和“f(a) f(b)<0”是函数 y=f(x)在区间 (a,b) 内有零点的充分不必要条件。
问题:有几个零点?
x
a
b
x
a
b
思考:增加什么条件时,函数在区间(a,b)上只有一个零点?
(单调)
如果函数y =f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且f(a) ·f(b)<0,则函数在(a,b)内有零点.
结论:不确定
x
y
0
下图中在区间[a,b]内有几个零点?
探究
什么情况下只有唯一一个零点?
端点函数值异号的
单调函数
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且f(a)·f(b) < 0,且是单调函数,那么这个函数在(a,b)内必有唯一的一个零点。
f(a)·f(b) < 0
+
函数图象连续
则函数有唯一零点
+
函数在区间内单调
函数零点方程根,
形数本是同根生。
函数零点端点判,
图象连续不能忘。
(1)已知函数y=f (x)在区间[a,b]上连续,且f (a) ·f(b) < 0,则f(x)在区间(a,b)内有且仅有一个零点. ( )
(3)已知函数y=f (x)在区间[a,b]上连续且在区间(a,b)内存在零点.,则f(x)必满足f (a) ·f(b) < 0. ( )
(2)已知函数y=f (x)在区间[a,b]上连续,且f (a) ·f(b) ≥0,则f(x)在区间(a,b)内没有零点. ( )
(4)已知函数y=f (x)在区间[a,b]上连续的单调函数且满足
f (a) ·f(b) < 0,则函数y=f (x)区间(a,b)上有且仅有一个
零点。 ( )
例2 判断正误,若不正确,请使用函数图象举出反例
正反例证,熟悉定理
x
O
y
a
b
(1)图
x
y
o
a
b
(2)图
x
b
a
o
y
(3)图
小结论:定理不能确定零点的个数;不满足定理条件时依然可能有零点;定理中的“连续不断”是必不可少的条件。
练习2::若函数y=5x2-7x-1在区间[a,b]上的图象是连续不断的曲线,且函数y=5x2-7x-1在(a,b)内有零点,则f(a)·f(b)的值( )
A、大于0 B、小于0 C、无法判断 D、等于零
【零点存在定理应用】
练习1:函数f(x)=x3+x-1在下列哪个区间有零点( )
A.(-2,-1) B.(0,1) C.(1,2) D.(2,3)
C
B
P143 例1 求方程f(x)=lnx+2x-6的实数解的个数.
解:令函数f(x)=lnx+2x-6,因为函数f(x)的定义域为(0,+∞)
设x1,x2为(0,+∞)上的任意两个实数,且x1< x2,
f(x1)-f(x2)=lnx1+2x1-6-(lnx2+2x2-6)=lnx1+2x1-6-lnx2-2x2+6
=lnx1-lnx2+2x1-2x2
因为x1< x2,所以x1-x2<0,
f(x1)-f(x2)<0,即f(x1)所以函数f(x)=lnx+2x-6在(0,+∞)上单调递增.
f(2)=ln2+4-6=ln2-2=ln2-2lne=ln2-lne2<0,
f(3)=ln3+6-6=ln3>0,
函数f(x)=lnx+2x-6在(2,3)上存在零点.
所以函数f(x)=lnx+2x-6有一个零点,即方程f(x)=lnx+2x-6有唯一解.
y=-2x +6
y=lnx
6
0
x
1
2
3
4
y
如图可知,只有一个交点,即方程只有一根.
方法2:
零点的求法(2)
图像法
即求 lnx=6-2x的根的个数,
即判断函数y=lnx与函数y=6-2x图像的交点个数
体现数学中数形结合、函数与方程的思想、转化与化归思想
P143 例1 求方程f(x)=lnx+2x-6的实数解的个数.
【变式提升】 求方程2-x =x的根的个数,并确定根所在的区间[n,n+1](n∈Z).
解:求方程2-x =x的根的个数,即求方程
的根的个数,即在判断函数y=x 与 的图象交点个数。由图可知只有一解。
y=x
1
O
x
1
2
3
4
y
估算f(x)在各整数处的取值的正负:
令
由上表可知,方程的根所在区间为[0,1].
x
0
1
2
3
f(x)
-
+
+
+
数缺形时少直观,
形少数时难入微,
数形结合百般好,
隔离分家万事休。
函数零点的求法
代数法和图象法
课堂小结
作业:P88 练习 1 、2
(1)函数零点的概念;
(3)函数零点的存在性定理;
(4)学会函数与方程和数形结合的思想;
(5)函数的零点判断方法
①方程法 ②图象法 ③定理法
(2)方程的根与函数的零点;
函数零点方程根,
图象连续总有痕。
数形本是同根生,
端值计算是根本。
借问零点何处有,
端值互异零点生。
温
馨
提
示
如果你不知道你要到哪儿去,那通常你哪儿也去不了。
大家树立远大理想,找寻理想实现的方法,在求解的道路上奋发图强!
练习2:
4.5.1函数的零点与方程的解
hán shù de línɡ diǎn yǔ fānɡ chénɡ de jiě
今天我们可以从教科书中了解各式各样方程的解法,但在数学发展史上,方程的求解却经历了相当漫长的岁月.
约公元50-100年前编成的《九章算术》给出了一次方程、二次方程和正系数三次方程的求根方法.
13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法.
阿拉伯数学家花拉子米(约780~约850)给出了一次方程和二次方程的一般解法.
阿贝尔(1802~1829)挪威数学家.证明了五次以上一般方程没有求根公式.
卡尔达诺,意大利数学家,他第一个发
表了三次代数方程一般解法的卡尔达诺
公式,也称卡当公式(解法的思路来自
塔塔利亚,两人因此结怨,争论多年)。
他的学生费拉里第一个求出四次方程的
代数解。
韦达是法国十六世纪最有影响的数学家之
一。第一个引进系统的代数符号,并对方
程论做了改进。韦达讨论了方程根的各种
有理变换,发现了方程根与系数之间的关
系即“韦达定理” 。
初步探索 直观感知chū bù tàn suǒ zhí ɡuān ɡǎn zhī
1.求下列方程的根.
①x-2=0 ②x2-2x-3=0 ③log2x=0
2.画出下列函数的图象
①y=x-2 ②x2-2x-3=0 ③y=log2x
3
2
1
-1
-1
2
1
0
1
-1
-2
-1
-2
2
1
0
方程的根就是对应函数图象与x轴交点的横坐标
x
y
O
-1
3
思考:方程根与相应函数图象有什么联系?
其他函数与方程之间也有同样结果吗?
方程f(x)=0的实数根?函数y= f(x)图象与x轴交点的横坐标
0
x
y
x1
x2
x3
x4
y=f(x)
得到方程f(x)=0
实质:在函数y=f(x)中,令y=0
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点。
函数零点的定义:
零点是一个点吗?
注意: 函数的零点是一个实数,当自变量取该值时,其函数值等于零.
区别:
零点对于函数而言,根对于方程而言.
函数y=f(x)的零点与、方程f(x)=0的根、函数y=f(x)的图像与x轴的交点的横坐标的关系.
函数y=f(x)的零点
? 方程f(x)=0的实数根
? 函数y=f(x)的图象与x轴交点的横坐标.
探究 如何求函数的零点?
练习1:求下列函数的零点
1 方程法
2 图象法
思考:函数f(x)=lnx+2x-6是否有零点?如何判断?零点的个数?
第1组
第2组
探究 现在有两组镜头(如图),哪一组能说明她的行程一定曾渡河? ??
A
B
B
A
x
x
结论:第一组能说明她的行程一定曾渡河
若将河流抽象成x轴,前后的两个位置视为A、B两点。请大家用连续不断的曲线画出她的可能路径。
x
A
B
O
y
a
b
若所画曲线能表示为函数,设A点横坐标为a,B点横坐标为b,怎样才能保证函数在[a,b]内有零点?
a
b
a
A
B
B
A
若所画曲线能表示为函数,设A点横坐标为a,B点横坐标为b,怎样才能保证函数在[a,b]内有零点?
x
b
x
1. 一定有?有几个?一定没有?
2.怎样用数学符号表示零点存在的条件?
y
y
f(a)·f(b) < 0,即端点函数值异号
0
y
x
0
y
x
如果f(a)·f(b) < 0,但图象不是连续不断的,能否一定有零点?
端点函数值异号f(a)·f(b) < 0
+
函数图象连续
则函数有零点
如果函数y =f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且f(a) ·f(b)<0,则函数在(a,b)内有零点.即存在c∈(a,b),使得f(c)=0,这个c也就是方程的根.
零点存在性定理
注:只有上述两个条件同时满足,才能判断函数在指定区间内存在零点。
函数图像连续不断和f(a) ·f(b)<0是函数存在零点的充分条件
是不是必要条件?
函数存在零点 ? 函数图像连续不断和f(a) ·f(b)<0
?
[思考]
(1)若函数y=f(x)在区间(a,b)内有零点,且f(a)·f(b)<0则一定能够得出f(x)在[a,b]上连续么?
不一定
x
a
b
c1
c2
y
x
a
b
c1
c2
y
(2)函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,若函数y=f(x)在区间(a, b)内有零点,一定能得出f(a)·f(b)<0的结论吗?
“函数图像在给定区间[a,b]上连续”和“f(a) f(b)<0”是函数 y=f(x)在区间 (a,b) 内有零点的充分不必要条件。
问题:有几个零点?
x
a
b
x
a
b
思考:增加什么条件时,函数在区间(a,b)上只有一个零点?
(单调)
如果函数y =f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且f(a) ·f(b)<0,则函数在(a,b)内有零点.
结论:不确定
x
y
0
下图中在区间[a,b]内有几个零点?
探究
什么情况下只有唯一一个零点?
端点函数值异号的
单调函数
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且f(a)·f(b) < 0,且是单调函数,那么这个函数在(a,b)内必有唯一的一个零点。
f(a)·f(b) < 0
+
函数图象连续
则函数有唯一零点
+
函数在区间内单调
函数零点方程根,
形数本是同根生。
函数零点端点判,
图象连续不能忘。
(1)已知函数y=f (x)在区间[a,b]上连续,且f (a) ·f(b) < 0,则f(x)在区间(a,b)内有且仅有一个零点. ( )
(3)已知函数y=f (x)在区间[a,b]上连续且在区间(a,b)内存在零点.,则f(x)必满足f (a) ·f(b) < 0. ( )
(2)已知函数y=f (x)在区间[a,b]上连续,且f (a) ·f(b) ≥0,则f(x)在区间(a,b)内没有零点. ( )
(4)已知函数y=f (x)在区间[a,b]上连续的单调函数且满足
f (a) ·f(b) < 0,则函数y=f (x)区间(a,b)上有且仅有一个
零点。 ( )
例2 判断正误,若不正确,请使用函数图象举出反例
正反例证,熟悉定理
x
O
y
a
b
(1)图
x
y
o
a
b
(2)图
x
b
a
o
y
(3)图
小结论:定理不能确定零点的个数;不满足定理条件时依然可能有零点;定理中的“连续不断”是必不可少的条件。
练习2::若函数y=5x2-7x-1在区间[a,b]上的图象是连续不断的曲线,且函数y=5x2-7x-1在(a,b)内有零点,则f(a)·f(b)的值( )
A、大于0 B、小于0 C、无法判断 D、等于零
【零点存在定理应用】
练习1:函数f(x)=x3+x-1在下列哪个区间有零点( )
A.(-2,-1) B.(0,1) C.(1,2) D.(2,3)
C
B
P143 例1 求方程f(x)=lnx+2x-6的实数解的个数.
解:令函数f(x)=lnx+2x-6,因为函数f(x)的定义域为(0,+∞)
设x1,x2为(0,+∞)上的任意两个实数,且x1< x2,
f(x1)-f(x2)=lnx1+2x1-6-(lnx2+2x2-6)=lnx1+2x1-6-lnx2-2x2+6
=lnx1-lnx2+2x1-2x2
因为x1< x2,所以x1-x2<0,
f(x1)-f(x2)<0,即f(x1)
f(2)=ln2+4-6=ln2-2=ln2-2lne=ln2-lne2<0,
f(3)=ln3+6-6=ln3>0,
函数f(x)=lnx+2x-6在(2,3)上存在零点.
所以函数f(x)=lnx+2x-6有一个零点,即方程f(x)=lnx+2x-6有唯一解.
y=-2x +6
y=lnx
6
0
x
1
2
3
4
y
如图可知,只有一个交点,即方程只有一根.
方法2:
零点的求法(2)
图像法
即求 lnx=6-2x的根的个数,
即判断函数y=lnx与函数y=6-2x图像的交点个数
体现数学中数形结合、函数与方程的思想、转化与化归思想
P143 例1 求方程f(x)=lnx+2x-6的实数解的个数.
【变式提升】 求方程2-x =x的根的个数,并确定根所在的区间[n,n+1](n∈Z).
解:求方程2-x =x的根的个数,即求方程
的根的个数,即在判断函数y=x 与 的图象交点个数。由图可知只有一解。
y=x
1
O
x
1
2
3
4
y
估算f(x)在各整数处的取值的正负:
令
由上表可知,方程的根所在区间为[0,1].
x
0
1
2
3
f(x)
-
+
+
+
数缺形时少直观,
形少数时难入微,
数形结合百般好,
隔离分家万事休。
函数零点的求法
代数法和图象法
课堂小结
作业:P88 练习 1 、2
(1)函数零点的概念;
(3)函数零点的存在性定理;
(4)学会函数与方程和数形结合的思想;
(5)函数的零点判断方法
①方程法 ②图象法 ③定理法
(2)方程的根与函数的零点;
函数零点方程根,
图象连续总有痕。
数形本是同根生,
端值计算是根本。
借问零点何处有,
端值互异零点生。
温
馨
提
示
如果你不知道你要到哪儿去,那通常你哪儿也去不了。
大家树立远大理想,找寻理想实现的方法,在求解的道路上奋发图强!
练习2:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
