5.1.1任意角-【新教材】人教A版(2019)高中数学必修第一册课件(21张PPT)
文档属性
| 名称 | 5.1.1任意角-【新教材】人教A版(2019)高中数学必修第一册课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 16.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:50:24 | ||
图片预览







文档简介
第五章 三角函数
人教A版高中数学必修第一册
第五章 章节引入
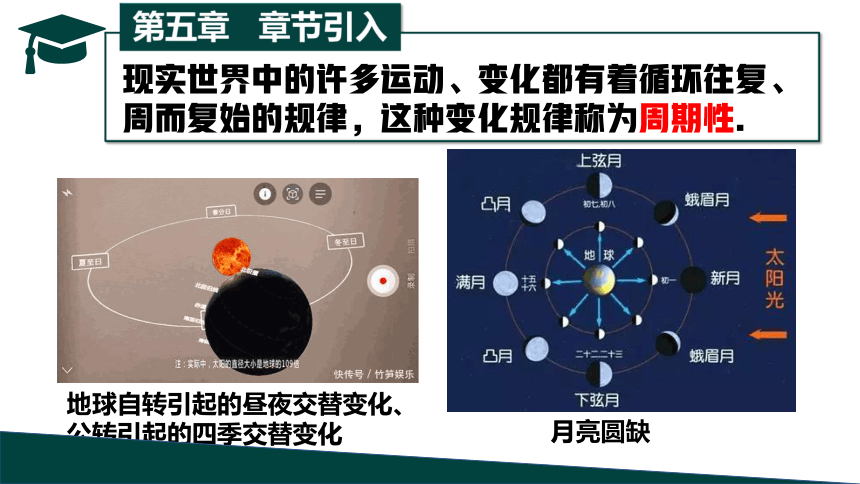
现实世界中的许多运动、变化都有着循环往复、周而复始的规律,这种变化规律称为周期性.
地球自转引起的昼夜交替变化、公转引起的四季交替变化
月亮圆缺
第五章 章节引入
现实世界中的许多运动、变化都有着循环往复、周而复始的规律,这种变化规律称为周期性.
潮汐变化
物体匀速圆周运动时的位置变化
第五章 章节引入
本章我们将学习刻画周期性变化规律的函数——三角函数.
背景
概念
图像与性质
应用
函数的一般研究步骤
本章研究内容:
①三角函数是怎样的函数?②三角函数具有哪些特征?
③如何利用三角函数模型刻画各种周期性变化现象?
第五章 三角函数
5.1 任意角和弧度制
人教A版高中数学必修第一册
5.1.1 任意角
A
P
O
ɑ
思考1:如何刻画点P的位置变化?
圆周运动是一种常见的周期性变化现象.
思考2:初中学过角的范围00~3600,点P旋转一周即为3600,再旋转所得的角如何表示?
借助角ɑ的大小变化刻画点P的位置变化.
有必要扩充角的范围!
我们生活中随处可见的角
体操动作“李小鹏跳”:2002年在匈牙利世锦赛上,李小鹏在跳马时做出的“踺子后手翻转体180度接直体前空翻转体900度”
在体操、花样滑冰、跳台跳水等比赛中,常常听到“转体2周”、“转体3周半”这些动作名词,你知道他们转了多少角吗?
(1)时钟从12:00到12:15,分针转过了多少度?
(2)时钟从12:00到13:15,分针转过了多少度?
机械齿轮
生活中很多的角并不是静态的
引入新的角的定义、分类:
平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.射线OA、OB分别是角的始边和终边,端点O为角的顶点。
始边
终边
顶点
B
A
O
旋转方向
引入新的角的定义、分类:
逆时针方向旋转所形成的角叫做正角
O
A(B)
没有作任何旋转形成的角叫做零角
顺时针方向旋转所形成的角叫做负角
A
B
O
A
B
O
{
角
正角
负角
零角
(1)时钟从12:00到12:15,分针转过了多少度?
(2)时钟从12:00到13:15,分针转过了多少度?
角的关系和加减运算
角相等:旋转方向和旋转量相等,记为:α=β
α+β:把角α的终边再旋转角β
-α:与角α旋转方向相反,旋转量相同,称作角α的相反角;α-β=α+(-β)
角的分类
为了进一步研究角的需要,我们常在直角坐标系内讨论角,并使角的顶点与原点重合,角的始边与x轴的非负半轴重合,
思考2:对一个任意角,角的终边可能落在哪些位置?
思考1:你能说说在直角坐标系内讨论角的好处吗?
x
y
o
始边
终边
?
终边
终边
终边
?
?
?
?
?
?
非象限角(轴线角)
非象限角(轴线角)
随堂练习:P171 1 3
角和终边的关系
请画出下列各组角,并思考:
?一个角,对应几条终边?
?一条终边,对应几个角?它们有什么关系?
(1)300,-3300, 3900 (2) 1200, -2400,4800(3) 00 , -3600,600
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
角和终边的关系
?一个角,对应一条终边;
?一条终边,对应无数个角:终边相同的角
与α终边相同的角β可表示为:β=α+k·3600,k∈z,
即任一与角α终边相同的角,都可以表示成角α整数个周角的和.
例题讲解
例1 在0°~360°范围内,找出与-950°12′角终边相同的角,并判定它是第几象限角.
随堂练习
P171 4
【解析】∵-950°12′= 129°48′-3×360°,∴在0°~360°范围内, 与-950°12′角终边相同的角是129°48′, 它是第二限角.
关键是通过加减360°的整数倍,在0°~360°范围内找到终边相同的角.
例题讲解
例2 写出终边在y轴上的角的集合.
y轴非负半轴:α= 90°+k·360°,k∈Z ;
终边在y轴上:S={α|α=90°+k·180° ,k∈Z}.
终边在x轴上:S={α|α=0°+k·180° ,k∈Z}.
终边在坐标轴上:S={α|α=0°+k·90° ,k∈Z}.
y轴非正半轴:α= 270°+k·360°,k∈Z .
α= 90°+2k·180°,k∈Z ;
α= 90°+180°+2k·180°
=90°+(2k+1)·180°,k∈Z .
例题讲解
例3 写出终边在y=x上的角的集合S,S中满足不等式-360°≤β≤720°的元素β有哪些.
【解析】S={β|β=45°+k·180°,k∈Z}.
S中适合不等式-360°≤β<720°的元素有:
-315°,-135°,45°,225°,405°,585°.
终边在第一象限的角的集合是什么?
终边在第一象限的角的集合是什么?
终边在第一象限的角的集合是什么?
终边在第一象限的角的集合是什么?
{α|=0°+k·360°<α<90°+k·360°,k∈Z}.
{α|=90°+k·360°<α<180°+k·360°,k∈Z}.
{α|=180°+k·360°<α<270°+k·360°,k∈Z}.
{α|=270°+k·360°<α<360°+k·360°,k∈Z}.
随堂练习
P171 4
课堂小结:
任意角
1.角的定义:顶点、始边、终边
2.角的分类(旋转方向):正角、负角和零角
(终边在坐标轴上的位置)象限角和轴线角3.终边相同的角集合表示:β=α+k·360°,k∈Z,
谢谢大家
人教版高中数学必修四
人教A版高中数学必修第一册
第五章 章节引入
现实世界中的许多运动、变化都有着循环往复、周而复始的规律,这种变化规律称为周期性.
地球自转引起的昼夜交替变化、公转引起的四季交替变化
月亮圆缺
第五章 章节引入
现实世界中的许多运动、变化都有着循环往复、周而复始的规律,这种变化规律称为周期性.
潮汐变化
物体匀速圆周运动时的位置变化
第五章 章节引入
本章我们将学习刻画周期性变化规律的函数——三角函数.
背景
概念
图像与性质
应用
函数的一般研究步骤
本章研究内容:
①三角函数是怎样的函数?②三角函数具有哪些特征?
③如何利用三角函数模型刻画各种周期性变化现象?
第五章 三角函数
5.1 任意角和弧度制
人教A版高中数学必修第一册
5.1.1 任意角
A
P
O
ɑ
思考1:如何刻画点P的位置变化?
圆周运动是一种常见的周期性变化现象.
思考2:初中学过角的范围00~3600,点P旋转一周即为3600,再旋转所得的角如何表示?
借助角ɑ的大小变化刻画点P的位置变化.
有必要扩充角的范围!
我们生活中随处可见的角
体操动作“李小鹏跳”:2002年在匈牙利世锦赛上,李小鹏在跳马时做出的“踺子后手翻转体180度接直体前空翻转体900度”
在体操、花样滑冰、跳台跳水等比赛中,常常听到“转体2周”、“转体3周半”这些动作名词,你知道他们转了多少角吗?
(1)时钟从12:00到12:15,分针转过了多少度?
(2)时钟从12:00到13:15,分针转过了多少度?
机械齿轮
生活中很多的角并不是静态的
引入新的角的定义、分类:
平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.射线OA、OB分别是角的始边和终边,端点O为角的顶点。
始边
终边
顶点
B
A
O
旋转方向
引入新的角的定义、分类:
逆时针方向旋转所形成的角叫做正角
O
A(B)
没有作任何旋转形成的角叫做零角
顺时针方向旋转所形成的角叫做负角
A
B
O
A
B
O
{
角
正角
负角
零角
(1)时钟从12:00到12:15,分针转过了多少度?
(2)时钟从12:00到13:15,分针转过了多少度?
角的关系和加减运算
角相等:旋转方向和旋转量相等,记为:α=β
α+β:把角α的终边再旋转角β
-α:与角α旋转方向相反,旋转量相同,称作角α的相反角;α-β=α+(-β)
角的分类
为了进一步研究角的需要,我们常在直角坐标系内讨论角,并使角的顶点与原点重合,角的始边与x轴的非负半轴重合,
思考2:对一个任意角,角的终边可能落在哪些位置?
思考1:你能说说在直角坐标系内讨论角的好处吗?
x
y
o
始边
终边
?
终边
终边
终边
?
?
?
?
?
?
非象限角(轴线角)
非象限角(轴线角)
随堂练习:P171 1 3
角和终边的关系
请画出下列各组角,并思考:
?一个角,对应几条终边?
?一条终边,对应几个角?它们有什么关系?
(1)300,-3300, 3900 (2) 1200, -2400,4800(3) 00 , -3600,600
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
角和终边的关系
?一个角,对应一条终边;
?一条终边,对应无数个角:终边相同的角
与α终边相同的角β可表示为:β=α+k·3600,k∈z,
即任一与角α终边相同的角,都可以表示成角α整数个周角的和.
例题讲解
例1 在0°~360°范围内,找出与-950°12′角终边相同的角,并判定它是第几象限角.
随堂练习
P171 4
【解析】∵-950°12′= 129°48′-3×360°,∴在0°~360°范围内, 与-950°12′角终边相同的角是129°48′, 它是第二限角.
关键是通过加减360°的整数倍,在0°~360°范围内找到终边相同的角.
例题讲解
例2 写出终边在y轴上的角的集合.
y轴非负半轴:α= 90°+k·360°,k∈Z ;
终边在y轴上:S={α|α=90°+k·180° ,k∈Z}.
终边在x轴上:S={α|α=0°+k·180° ,k∈Z}.
终边在坐标轴上:S={α|α=0°+k·90° ,k∈Z}.
y轴非正半轴:α= 270°+k·360°,k∈Z .
α= 90°+2k·180°,k∈Z ;
α= 90°+180°+2k·180°
=90°+(2k+1)·180°,k∈Z .
例题讲解
例3 写出终边在y=x上的角的集合S,S中满足不等式-360°≤β≤720°的元素β有哪些.
【解析】S={β|β=45°+k·180°,k∈Z}.
S中适合不等式-360°≤β<720°的元素有:
-315°,-135°,45°,225°,405°,585°.
终边在第一象限的角的集合是什么?
终边在第一象限的角的集合是什么?
终边在第一象限的角的集合是什么?
终边在第一象限的角的集合是什么?
{α|=0°+k·360°<α<90°+k·360°,k∈Z}.
{α|=90°+k·360°<α<180°+k·360°,k∈Z}.
{α|=180°+k·360°<α<270°+k·360°,k∈Z}.
{α|=270°+k·360°<α<360°+k·360°,k∈Z}.
随堂练习
P171 4
课堂小结:
任意角
1.角的定义:顶点、始边、终边
2.角的分类(旋转方向):正角、负角和零角
(终边在坐标轴上的位置)象限角和轴线角3.终边相同的角集合表示:β=α+k·360°,k∈Z,
谢谢大家
人教版高中数学必修四
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
