5.2.1三角函数的概念-【新教材】人教A版(2019)高中数学必修第一册课件 (20张PPT)
文档属性
| 名称 | 5.2.1三角函数的概念-【新教材】人教A版(2019)高中数学必修第一册课件 (20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1021.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:57:38 | ||
图片预览







文档简介
5.2.1
三角函数的概念
新高考新教材
高中数第一册第五章三角函数
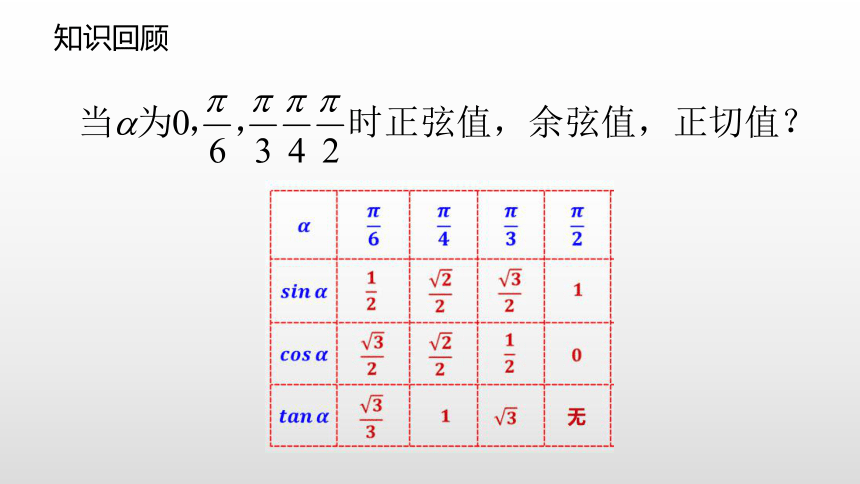
知识回顾
根据研究函数的经验,我们选择在坐标系上研究这个
问题.如图,以单位圆的圆心为原点, 以射线OA为
轴的非负半轴,建立直角坐标系.则A(1,0),P
射线OA从 轴非负半轴开始,绕点O按逆时针方向
旋转角α,终止位置为OP.
?
?
?
三角函数的概念
【探究】当 时,点P的坐标是什么?当 或 时,
点P的坐标又是什么?给定一个角α,它的终边OP
与单位圆的交点P的坐标是唯一确定的吗?
?
?
P
P
【结论】一般地,任意给定一个角α∈R,它的终边OP与单位圆的交点P的坐标,无
论是横坐标 还是纵坐标 ,都是唯一确定的.所以,点P的横坐标 和
纵坐标 都是角α的函数.
?
?
?
?
可以看出,当 时,α的终边始终在y轴上,时 ,即此时tanα无意义.除此之外,正切tanα与实数α是一一对应的,所以它们之间也是函数关系,我们称 为正切函数.
?
?
?
?
=tanα ( )
【总结】三角函数可以看成是以实数α(α为弧度)为自变量,以
单位圆上点的坐标或坐标的比值为函数值的函数.
(1)正弦函数:
(2)余弦函数:
(3)正切函数:
?
?
?
角
实数
(角的弧度)
三角
函数值
我们把正弦函数、余弦函数和正切函数统称为三角函数.
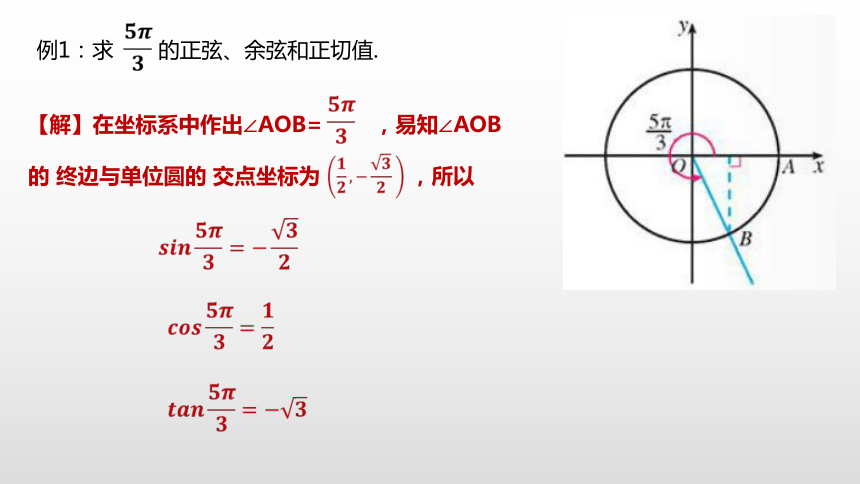
例1:求 的正弦、余弦和正切值.
【解】在坐标系中作出∠AOB= ,易知∠AOB的 终边与单位圆的 交点坐标为 ,所以
?
?
?
?
?
?
课本第179-180练习1-4
+
+
+
+
+
-
-
-
-
-
-
记忆口诀:一全正,二正弦,三正切,四余弦
例1:求证:角θ为第三象限角的充要条件为
【证明】首先证明充分性,
?
因为sinθ<0成立,所以θ角的终边位于第三或者第四象限,
也可能和Y轴的负半轴重合;
又因为cosθ>0成立,所以θ角的终边位于第一或者第三象限,
所以必要性成立,即充要性成立.
综合可知Θ为第三象限角.
再证明必要性,
因为θ是第三象限角,根据定义有sinθ<0, cosθ>0,
公式一说明了角和三角函数值的对应关系是多角对一值的关系:
即给定一个角,它的三角函数值只要存在,就是唯一的;
反过来,给定一个三角函数值,却有无数个角与之对应.
诱导公式一
正
正
正
负
负
零
三角函数的概念
新高考新教材
高中数第一册第五章三角函数
知识回顾
根据研究函数的经验,我们选择在坐标系上研究这个
问题.如图,以单位圆的圆心为原点, 以射线OA为
轴的非负半轴,建立直角坐标系.则A(1,0),P
射线OA从 轴非负半轴开始,绕点O按逆时针方向
旋转角α,终止位置为OP.
?
?
?
三角函数的概念
【探究】当 时,点P的坐标是什么?当 或 时,
点P的坐标又是什么?给定一个角α,它的终边OP
与单位圆的交点P的坐标是唯一确定的吗?
?
?
P
P
【结论】一般地,任意给定一个角α∈R,它的终边OP与单位圆的交点P的坐标,无
论是横坐标 还是纵坐标 ,都是唯一确定的.所以,点P的横坐标 和
纵坐标 都是角α的函数.
?
?
?
?
可以看出,当 时,α的终边始终在y轴上,时 ,即此时tanα无意义.除此之外,正切tanα与实数α是一一对应的,所以它们之间也是函数关系,我们称 为正切函数.
?
?
?
?
=tanα ( )
【总结】三角函数可以看成是以实数α(α为弧度)为自变量,以
单位圆上点的坐标或坐标的比值为函数值的函数.
(1)正弦函数:
(2)余弦函数:
(3)正切函数:
?
?
?
角
实数
(角的弧度)
三角
函数值
我们把正弦函数、余弦函数和正切函数统称为三角函数.
例1:求 的正弦、余弦和正切值.
【解】在坐标系中作出∠AOB= ,易知∠AOB的 终边与单位圆的 交点坐标为 ,所以
?
?
?
?
?
?
课本第179-180练习1-4
+
+
+
+
+
-
-
-
-
-
-
记忆口诀:一全正,二正弦,三正切,四余弦
例1:求证:角θ为第三象限角的充要条件为
【证明】首先证明充分性,
?
因为sinθ<0成立,所以θ角的终边位于第三或者第四象限,
也可能和Y轴的负半轴重合;
又因为cosθ>0成立,所以θ角的终边位于第一或者第三象限,
所以必要性成立,即充要性成立.
综合可知Θ为第三象限角.
再证明必要性,
因为θ是第三象限角,根据定义有sinθ<0, cosθ>0,
公式一说明了角和三角函数值的对应关系是多角对一值的关系:
即给定一个角,它的三角函数值只要存在,就是唯一的;
反过来,给定一个三角函数值,却有无数个角与之对应.
诱导公式一
正
正
正
负
负
零
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
