高中数学人教A版(2019)必修第—册第四章4.5.1函数的零点与方程的解 课件(24张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)必修第—册第四章4.5.1函数的零点与方程的解 课件(24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 724.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 20:46:53 | ||
图片预览







文档简介
4.5.1 函数零点与方程的解
第五章 函数的应用(二)
1.结合二次函数的图象,了解函数的零点与方程根的联系.
2. 会求简单函数的零点、零点个数及零点所在的大致区间.
学习目标
怎么解呢?
提出问题
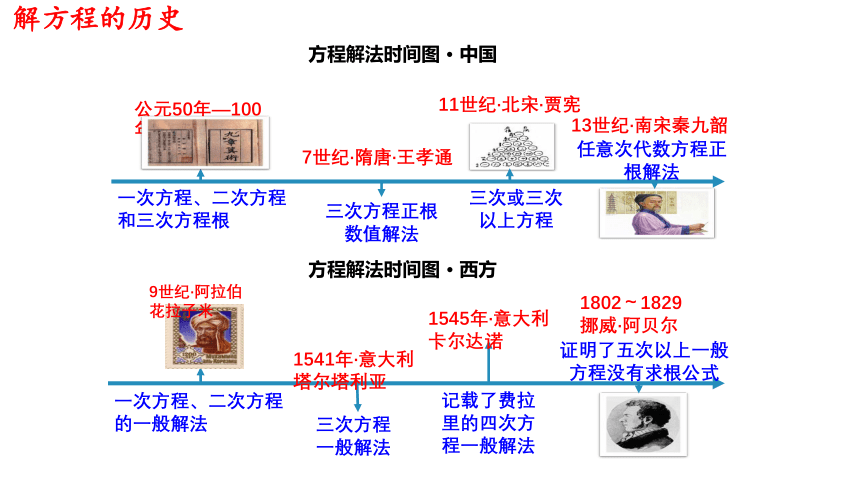
方程解法时间图 · 中国
公元50年—100年
一次方程、二次方程
和三次方程根
11世纪·北宋·贾宪
三次方程正根数值解法
13世纪·南宋秦九韶
任意次代数方程正根解法
7世纪·隋唐·王孝通
三次或三次以上方程
方程解法时间图 · 西方
一次方程、二次方程
的一般解法
1541年·意大利
塔尔塔利亚
三次方程一般解法
1802~1829
挪威·阿贝尔
证明了五次以上一般方程没有求根公式
记载了费拉里的四次方程一般解法
9世纪·阿拉伯
花拉子米
1545年·意大利
卡尔达诺
解方程的历史
方程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
y= x2-2x+1
函数
函
数
的
图
象
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
函数的图象
与x轴的交点
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
.
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
5
4
3
.
.
.
.
.
y
x
0
-1
2
1
1
2
y= x2-2x+3
思考:方程的根与函数的图象和x轴交点的横坐标有什么关系?
问题探究
观察函数的图象思考:
1.方程的根与函数的图象和x轴交点的横坐标有什么关系?
1.方程根的个数和对应函数与x轴交点个数相同.
2.方程的根是函数与x轴交点的横坐标.
3.若一元二次方程无实数根,则相应的二次函数图像与x轴无交点.
问题探究
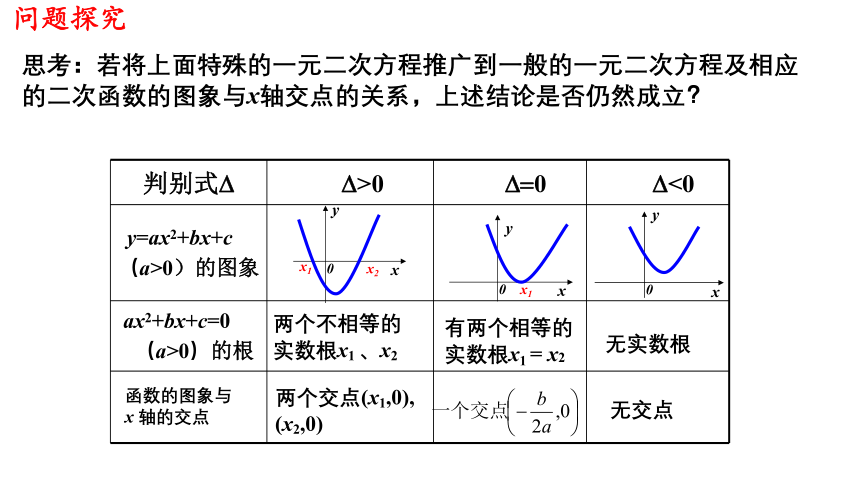
思考:若将上面特殊的一元二次方程推广到一般的一元二次方程及相应的二次函数的图象与x轴交点的关系,上述结论是否仍然成立?
判别式?
?>0
??0
?<0
y=ax2+bx+c
(a>0)的图象
ax2+bx+c=0
(a>0)的根
x
y
x1
x2
0
x
y
0
x1
x
y
0
函数的图象与
x 轴的交点
两个交点(x1,0), (x2,0)
无交点
有两个相等的实数根x1 = x2
无实数根
两个不相等的实数根x1 、x2
问题探究
思考:若将上面特殊的一元二次方程推广到一般的一元二次方程及相应的
二次函数的图象与x轴交点的关系,上述结论是否仍然成立?
一元二次方程的根就是相应的二次函数图象与x轴交点的横坐标。
若一元二次方程无实数根,则相应的二次函数图像与x轴无交点。
问题探究
推广到更一般的情况,得:
零点:
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
函数的零点是一个点吗?
问题1:
零点不是一个点,零点指的是一个实数.
问题2:
试归纳函数零点的等价说法?
方程f (x)=0
有实数根
函数y=f (x)
有零点.
函数y=f (x)的图
象与x轴有交点
概念解析
跟踪训练
跟踪训练
观察函数的图象并填空:
1.在区间(a,b)上f(a)·f(b)_____0(“<”或“>”).
在区间(a,b)上______(有/无)零点;
2. 在区间(b,c)上f(b)·f(c) _____ 0(“<”或“>”).
在区间(b,c)上______(有/无)零点;
3.在区间(c,d)上f(c)·f(d) _____ 0(“<”或”>”).
在区间(c,d)上______(有/无)零点;
4.在区间(e,g)上f(e)·f(g) _____ 0(“<”或”>”).
在区间(e,g)上______(有/无)零点;
有
<
有
<
有
<
x
y
O
a
b
c
d
问题2:在怎样的条件下,函数y=f(x)在区间[a,b]上存在零点?
O
y
x
g
e
<
无
问题探究
零点存在性定理:
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点.
即存在c∈(a,b),使得f(c)=0,这个c就是方程f(x)=0的根.
定理解读
思考1:为什么强调“函数y=f(x)在区间[a,b]上的图象一条不间断的曲线”?如果函数图象不连续,或者y=f(x)不满足f(a)·f(b) <0,那么零点存在性定理还成立吗?
x
y
O
a
b
O
y
x
b
a
O
y
x
b
a
O
y
x
b
a
定理解读
?
?
典例解析
?
?
【答案】C
当堂达标
课堂小结
第五章 函数的应用(二)
1.结合二次函数的图象,了解函数的零点与方程根的联系.
2. 会求简单函数的零点、零点个数及零点所在的大致区间.
学习目标
怎么解呢?
提出问题
方程解法时间图 · 中国
公元50年—100年
一次方程、二次方程
和三次方程根
11世纪·北宋·贾宪
三次方程正根数值解法
13世纪·南宋秦九韶
任意次代数方程正根解法
7世纪·隋唐·王孝通
三次或三次以上方程
方程解法时间图 · 西方
一次方程、二次方程
的一般解法
1541年·意大利
塔尔塔利亚
三次方程一般解法
1802~1829
挪威·阿贝尔
证明了五次以上一般方程没有求根公式
记载了费拉里的四次方程一般解法
9世纪·阿拉伯
花拉子米
1545年·意大利
卡尔达诺
解方程的历史
方程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
y= x2-2x+1
函数
函
数
的
图
象
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
函数的图象
与x轴的交点
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
.
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
5
4
3
.
.
.
.
.
y
x
0
-1
2
1
1
2
y= x2-2x+3
思考:方程的根与函数的图象和x轴交点的横坐标有什么关系?
问题探究
观察函数的图象思考:
1.方程的根与函数的图象和x轴交点的横坐标有什么关系?
1.方程根的个数和对应函数与x轴交点个数相同.
2.方程的根是函数与x轴交点的横坐标.
3.若一元二次方程无实数根,则相应的二次函数图像与x轴无交点.
问题探究
思考:若将上面特殊的一元二次方程推广到一般的一元二次方程及相应的二次函数的图象与x轴交点的关系,上述结论是否仍然成立?
判别式?
?>0
??0
?<0
y=ax2+bx+c
(a>0)的图象
ax2+bx+c=0
(a>0)的根
x
y
x1
x2
0
x
y
0
x1
x
y
0
函数的图象与
x 轴的交点
两个交点(x1,0), (x2,0)
无交点
有两个相等的实数根x1 = x2
无实数根
两个不相等的实数根x1 、x2
问题探究
思考:若将上面特殊的一元二次方程推广到一般的一元二次方程及相应的
二次函数的图象与x轴交点的关系,上述结论是否仍然成立?
一元二次方程的根就是相应的二次函数图象与x轴交点的横坐标。
若一元二次方程无实数根,则相应的二次函数图像与x轴无交点。
问题探究
推广到更一般的情况,得:
零点:
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
函数的零点是一个点吗?
问题1:
零点不是一个点,零点指的是一个实数.
问题2:
试归纳函数零点的等价说法?
方程f (x)=0
有实数根
函数y=f (x)
有零点.
函数y=f (x)的图
象与x轴有交点
概念解析
跟踪训练
跟踪训练
观察函数的图象并填空:
1.在区间(a,b)上f(a)·f(b)_____0(“<”或“>”).
在区间(a,b)上______(有/无)零点;
2. 在区间(b,c)上f(b)·f(c) _____ 0(“<”或“>”).
在区间(b,c)上______(有/无)零点;
3.在区间(c,d)上f(c)·f(d) _____ 0(“<”或”>”).
在区间(c,d)上______(有/无)零点;
4.在区间(e,g)上f(e)·f(g) _____ 0(“<”或”>”).
在区间(e,g)上______(有/无)零点;
有
<
有
<
有
<
x
y
O
a
b
c
d
问题2:在怎样的条件下,函数y=f(x)在区间[a,b]上存在零点?
O
y
x
g
e
<
无
问题探究
零点存在性定理:
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点.
即存在c∈(a,b),使得f(c)=0,这个c就是方程f(x)=0的根.
定理解读
思考1:为什么强调“函数y=f(x)在区间[a,b]上的图象一条不间断的曲线”?如果函数图象不连续,或者y=f(x)不满足f(a)·f(b) <0,那么零点存在性定理还成立吗?
x
y
O
a
b
O
y
x
b
a
O
y
x
b
a
O
y
x
b
a
定理解读
?
?
典例解析
?
?
【答案】C
当堂达标
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
