11.4一元一次不等式(第一课时) 课件(共27张PPT)
文档属性
| 名称 | 11.4一元一次不等式(第一课时) 课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 21:41:13 | ||
图片预览








文档简介
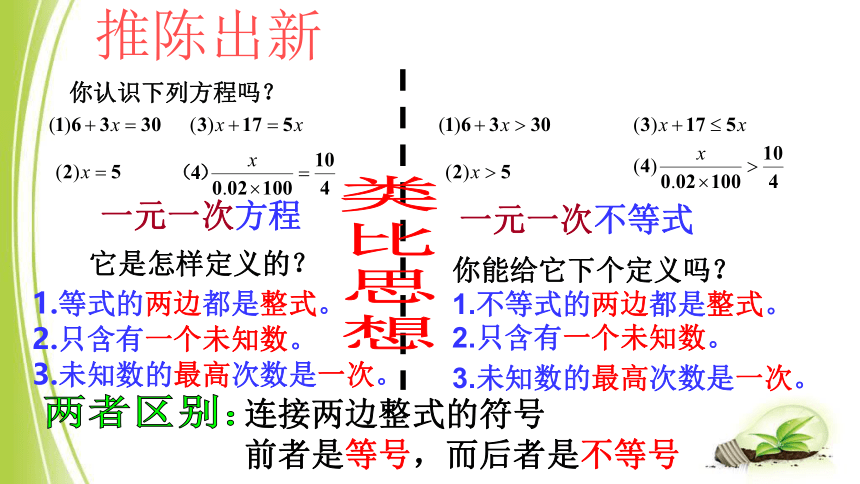
(共27张PPT)
鲁教版七年级下册第十一章
《一元一次不等式与一元一次不等式组》
第四节
一元一次不等式
第一课时
两者区别:
1.等式的两边都是整式。
2.只含有一个未知数。
3.未知数的最高次数是一次。
连接两边整式的符号
前者是等号,而后者是不等号
它是怎样定义的?
一元一次方程
一元一次不等式
你能给它下个定义吗?
1.不等式的两边都是整式。
2.只含有一个未知数。
3.未知数的最高次数是一次。
类
比
思
想
你认识下列方程吗?
推陈出新
定义:
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式。
发现新知
新的数学方法和概念,常常比解决问题本身更重要。
-----华罗庚
一个未知数
两边都是整式
未知数的最高次数是1
一元一次
不等式
要点梳理
下列不等式中哪些是一元一次不等式?
不是
(7)5x+3<0
(6)
4<5.1
(8)x>5
不是
是
是
不是
不是
是
不是
把握三个特征
牛刀小试
探究新知
将下列不等式化成“
”或“
”的形式,并说明每一步变形的依据
知识的积累绝不是简单的重复,需要我们不断探索,发现新知。
≥
解:两边同除以4,得
解:两边同除以
,得
x≤-2
理论依据
性质1、不等式的两边都加(或减)同一个整式,不等号的方向不变。
性质2、不等式的两边都乘(或除以)同一个正数,不等号的方向不变。
性质3、不等式的两边都乘(或除以)同一个负数,不等号的方向改变。
探究新知
解:
两边都加-2x,得
3-x-2x<2x+6-2x
合并同类项,得
3-3x<6
两边都加-3,得
3-3x-3<6-3
合并同类项,得
-3x<3
两边都除以-3,得
x>-1
这个不等式的解集在数轴上表示如下:
再探新知
例1:
解不等式3-x<2x+6,并把它的解集表示在数轴上。
解方程:3-x=2x+6
解:
移项,得
-x-2x=6-3
合并同类项,得
-3x=3
两边都除以-3,得
x=-1
类比旧知
解:
两边都加-2x,得
3-x-2x<2x+6-2x
合并同类项,得
3-3x<6
两边都加-3,得
3-3x-3<6-3
合并同类项,得
-3x<3
两边都除以-3,得
x>-1
这个不等式的解集在数轴上表示如下:
再探新知
例1
解不等式3-x<2x+6,并把它的解集表示在数轴上。
3-x<
2x
+6
-x-2x
<
6-3
把不等式中的任何一项的符号改变后,从不等号的一边移到另一边,所得到的不等式仍成立。
——移项法则
注意
移项时,项的符号要改变,
不等号的方向不变。
要点提炼
例2
:解不等式
,并把它的解集表示在数轴上。
这个不等式的解集在数轴上表示如下:
解:去分母,得
去括号,得
移项、合并同类项,得
两边都除以5,得
内化提升
你能总结归纳解一元一次不等式的基本步骤吗?
1、去分母
2、去括号
3、移项
4、合并同类项
5、化系数为1
归纳总结
拓展延伸
下列不等式的解法正确吗?如果不正确,请改正。
(1)-2x<-4
解:两边同除以-2,得_____.
解:去分母,得
x<2
x>2
√
×
能力提高
×
√
在解一元一次不等式的步骤中,应该注意什么问题?
点拨强化
1、去分母时,不能漏乘不含分母的项;
2、去掉分母后,分子要用括号括起来;
3、移项时,项的符号要改变,不等号的方向不变;
4、化系数为1时,要注意不等号方向是否需要改变。
我选择
我喜欢
五个字母分别代表了五种难度的题目,请你选择
巩固新知
学习数学要多做习题,边做边思考,先知其然,然后知其所以然。
----苏步青
解不等式,并把它的解集表示在数轴上
我选择
我喜欢
6(x-1)>3+4x
我选择
我喜欢
解不等式,并把它的解集表示在数轴上
我选择
我喜欢
解不等式0.5x-3>-14-2.5x,把解集表示在数轴上,
并求出适合不等式的最小负整数。
解:移项、合并同类项,得
3x>-11
两边都除以3,得
x>
1
0
-1
-2
-3
-4
所以,
最小负整数解x=-3
已知函数y=3x+5
(1)当x取何值时,y>0?
(2)当x取何值时,y=0?
(3)当x取何值时,y<0?
我选择
我喜欢
我选择
我喜欢
1.不等式(a+1)x>
(a+1)的解集是x<1,则a的取值范围是(
)
A.
a<0
B.
a<1
C.
a<-1
D.
a>-1
2.已知y=3x-2,要使y<x,则x的取值范围是______________。
梳理反思
通过本节课的学习,
你有哪些收获(或疑惑)?
回顾
典例
巩固
应用
反思
???
会解一元一次不等式
提高归纳总结能力
积极参与,乐于交流
一元一次不等式
一元一次不等式的定义
类比的数学思想方法
合作意识,探究精神
盘点收获
达标检测
(1)求不等式
的正整数解
解不等式,并把它的解集表示在数轴上。
(3)已知关于x的方程3x+a=x-7的根是正数,求实数a的取值范围。
课后练习
1、随堂练习1
2、《伴你学》相关题目
一个国家只有数学蓬勃的发展,才能展现它国力的强大。数学的发展和至善和国家繁荣昌盛密切相关。——拿破仑
鲁教版七年级下册第十一章
《一元一次不等式与一元一次不等式组》
第四节
一元一次不等式
第一课时
两者区别:
1.等式的两边都是整式。
2.只含有一个未知数。
3.未知数的最高次数是一次。
连接两边整式的符号
前者是等号,而后者是不等号
它是怎样定义的?
一元一次方程
一元一次不等式
你能给它下个定义吗?
1.不等式的两边都是整式。
2.只含有一个未知数。
3.未知数的最高次数是一次。
类
比
思
想
你认识下列方程吗?
推陈出新
定义:
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式。
发现新知
新的数学方法和概念,常常比解决问题本身更重要。
-----华罗庚
一个未知数
两边都是整式
未知数的最高次数是1
一元一次
不等式
要点梳理
下列不等式中哪些是一元一次不等式?
不是
(7)5x+3<0
(6)
4<5.1
(8)x>5
不是
是
是
不是
不是
是
不是
把握三个特征
牛刀小试
探究新知
将下列不等式化成“
”或“
”的形式,并说明每一步变形的依据
知识的积累绝不是简单的重复,需要我们不断探索,发现新知。
≥
解:两边同除以4,得
解:两边同除以
,得
x≤-2
理论依据
性质1、不等式的两边都加(或减)同一个整式,不等号的方向不变。
性质2、不等式的两边都乘(或除以)同一个正数,不等号的方向不变。
性质3、不等式的两边都乘(或除以)同一个负数,不等号的方向改变。
探究新知
解:
两边都加-2x,得
3-x-2x<2x+6-2x
合并同类项,得
3-3x<6
两边都加-3,得
3-3x-3<6-3
合并同类项,得
-3x<3
两边都除以-3,得
x>-1
这个不等式的解集在数轴上表示如下:
再探新知
例1:
解不等式3-x<2x+6,并把它的解集表示在数轴上。
解方程:3-x=2x+6
解:
移项,得
-x-2x=6-3
合并同类项,得
-3x=3
两边都除以-3,得
x=-1
类比旧知
解:
两边都加-2x,得
3-x-2x<2x+6-2x
合并同类项,得
3-3x<6
两边都加-3,得
3-3x-3<6-3
合并同类项,得
-3x<3
两边都除以-3,得
x>-1
这个不等式的解集在数轴上表示如下:
再探新知
例1
解不等式3-x<2x+6,并把它的解集表示在数轴上。
3-x<
2x
+6
-x-2x
<
6-3
把不等式中的任何一项的符号改变后,从不等号的一边移到另一边,所得到的不等式仍成立。
——移项法则
注意
移项时,项的符号要改变,
不等号的方向不变。
要点提炼
例2
:解不等式
,并把它的解集表示在数轴上。
这个不等式的解集在数轴上表示如下:
解:去分母,得
去括号,得
移项、合并同类项,得
两边都除以5,得
内化提升
你能总结归纳解一元一次不等式的基本步骤吗?
1、去分母
2、去括号
3、移项
4、合并同类项
5、化系数为1
归纳总结
拓展延伸
下列不等式的解法正确吗?如果不正确,请改正。
(1)-2x<-4
解:两边同除以-2,得_____.
解:去分母,得
x<2
x>2
√
×
能力提高
×
√
在解一元一次不等式的步骤中,应该注意什么问题?
点拨强化
1、去分母时,不能漏乘不含分母的项;
2、去掉分母后,分子要用括号括起来;
3、移项时,项的符号要改变,不等号的方向不变;
4、化系数为1时,要注意不等号方向是否需要改变。
我选择
我喜欢
五个字母分别代表了五种难度的题目,请你选择
巩固新知
学习数学要多做习题,边做边思考,先知其然,然后知其所以然。
----苏步青
解不等式,并把它的解集表示在数轴上
我选择
我喜欢
6(x-1)>3+4x
我选择
我喜欢
解不等式,并把它的解集表示在数轴上
我选择
我喜欢
解不等式0.5x-3>-14-2.5x,把解集表示在数轴上,
并求出适合不等式的最小负整数。
解:移项、合并同类项,得
3x>-11
两边都除以3,得
x>
1
0
-1
-2
-3
-4
所以,
最小负整数解x=-3
已知函数y=3x+5
(1)当x取何值时,y>0?
(2)当x取何值时,y=0?
(3)当x取何值时,y<0?
我选择
我喜欢
我选择
我喜欢
1.不等式(a+1)x>
(a+1)的解集是x<1,则a的取值范围是(
)
A.
a<0
B.
a<1
C.
a<-1
D.
a>-1
2.已知y=3x-2,要使y<x,则x的取值范围是______________。
梳理反思
通过本节课的学习,
你有哪些收获(或疑惑)?
回顾
典例
巩固
应用
反思
???
会解一元一次不等式
提高归纳总结能力
积极参与,乐于交流
一元一次不等式
一元一次不等式的定义
类比的数学思想方法
合作意识,探究精神
盘点收获
达标检测
(1)求不等式
的正整数解
解不等式,并把它的解集表示在数轴上。
(3)已知关于x的方程3x+a=x-7的根是正数,求实数a的取值范围。
课后练习
1、随堂练习1
2、《伴你学》相关题目
一个国家只有数学蓬勃的发展,才能展现它国力的强大。数学的发展和至善和国家繁荣昌盛密切相关。——拿破仑
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
